Value Functions & Bellman Equations

Policies and Value Functions

Specifying Policies

• Policy에 대해 알아보자.

• 이번 강의에서는 각 state에 따른 action을 결정하는 policy distribution에 대해 배운다.

  • Stochastic policy와 deterministic policy의 차이를 이해하고 MDP가 주어졌을 때의 유효한 policy는 어떻게 생성하는지 알아보도록 하겠다.

• Deterministic policy notaion은 다음과 같다.

  • $\pi(s) = a$

    • 어떠한 state가 주어졌을 때의 action a를 각 state마다 matching하는 것을 말한다.

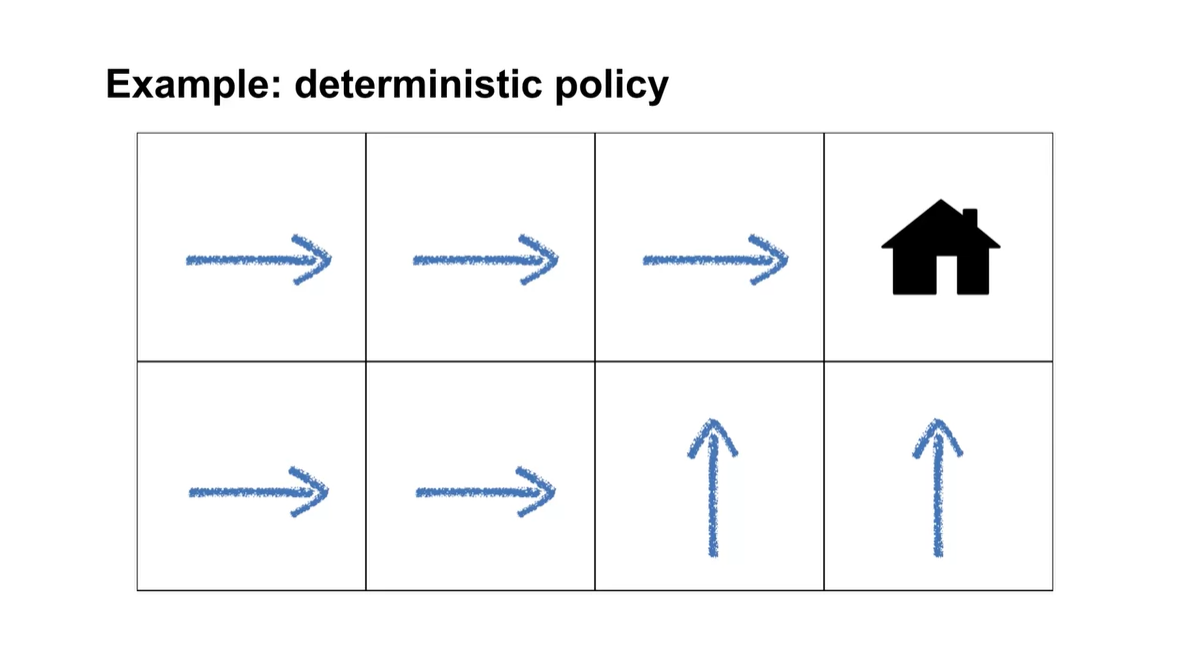
• 아래에 집을 찾아가기 위한 방향키 조절하는 예시가 나타나져 있다.

  • 이와 같은 예시가 deterministic policy 즉, 명확히 결정된 action이 존재하는 경우에 쓰인다.

• Stochastic policy notation은 $\pi (a | s)$로 표기한다.

  • 어떠한 state에서의 action random variable이 존재하며, 전체 확률의 합이 1인 상태의 확률 분포가 주어질 때 stochastic한 상황이라 정의한다.

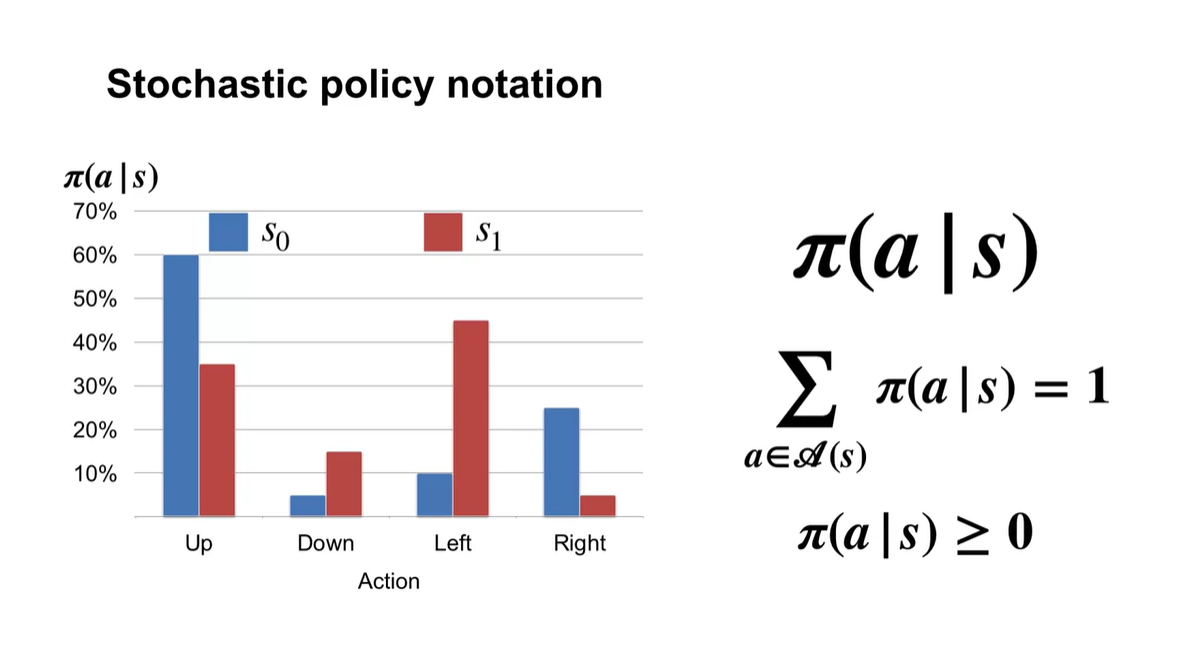
• 따라서 deterministic한 상황과는 다르게 stochastic policy는 action의 선택지가 확률로 표현되어 있는 것을 말한다.

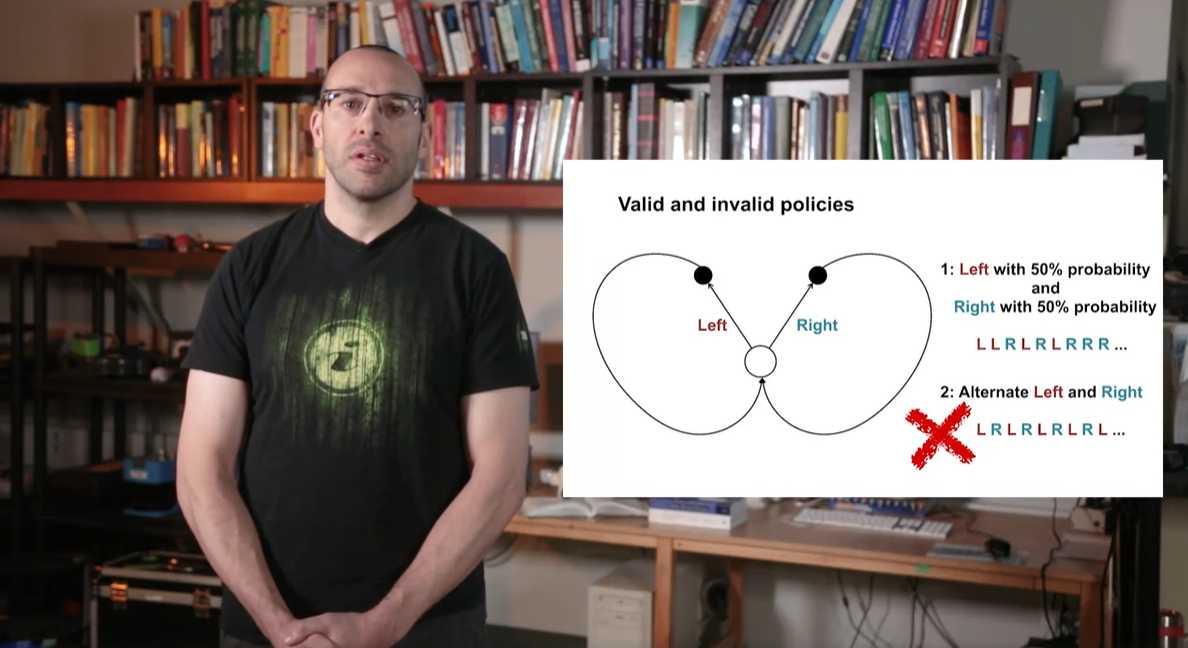
• 만약 Left와 Right의 선택지가 존재하고 각 probability가 50%의 확률을 가질 때, action을 선택하는 상황은 아래와 같을 수 있다.

  • 2번째 예시와 같이 이전 action을 참조하는 조건문(condition)이 사용되어서는 안된다.

• Summary

  • Policy는 오로지 current state에 의존한다.

Value Function

• Value function에 대해 알아보자.

• 이번 강의에서는 state-value function과 action-value function을 정의한다.

  • Value function과 policy의 관계를 정의내라고, 유효한 value function을 생성한 예시를 다뤄보도록 하겠다.

• State-value function의 notation은 다음과 같다.

  • $v_{\pi} (s) \doteq \mathbb E_{\pi}[G_t | S_t=s]$

    • Policy $\pi$를 고려한 state $s$에서의 전체 reward 기댓값을 의미한다.

• Action-value function의 notation은 다음과 같다.

  • $q_{\pi} (s, a) \doteq \mathbb E_{\pi}[G_t | S_t=s, A_t = a]$

    • State $s$와 취한 Action $a$가 주어졌을 때의 전체 reward 기댓값을 의미한다.

• Value function $v_{\pi}(s)$는 미래의 모든 경우의 수를 고려한 최적의 solution이라 할 수 있다.

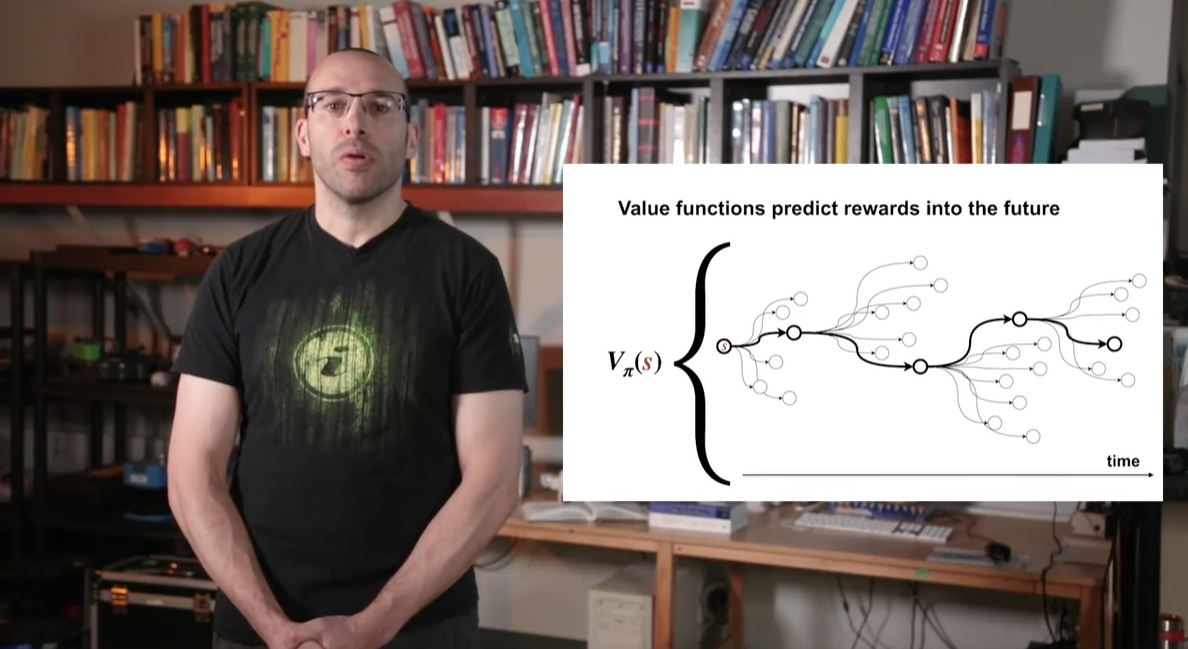
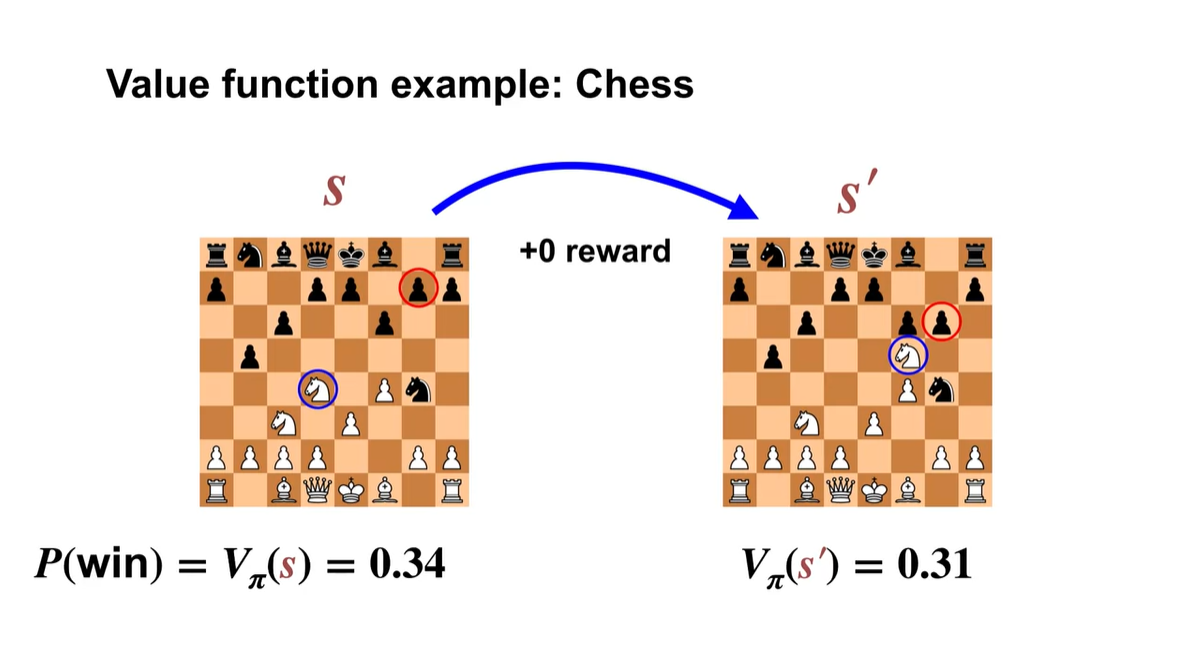
• Chess를 두는 상황을 가정해보자.

  • 정책 $\pi$를 따를 경우, 상태 가치는 단순히 이길 확률 $P(win)$이다.

    • 처음 $s$로부터 다음 $s'$으로 transition될 때, 아무런 reward를 받지 못하여 value $v_{\pi}(s')$가 감소하였다.

    • 남은 게임 동안 정책 $\pi$를 계속해서 따르게 된다면 게임을 지고 말 것이다.

      • 이렇듯 action-value function을 사용하면 각 움직임의 승리 확률을 평가할 수 있다.

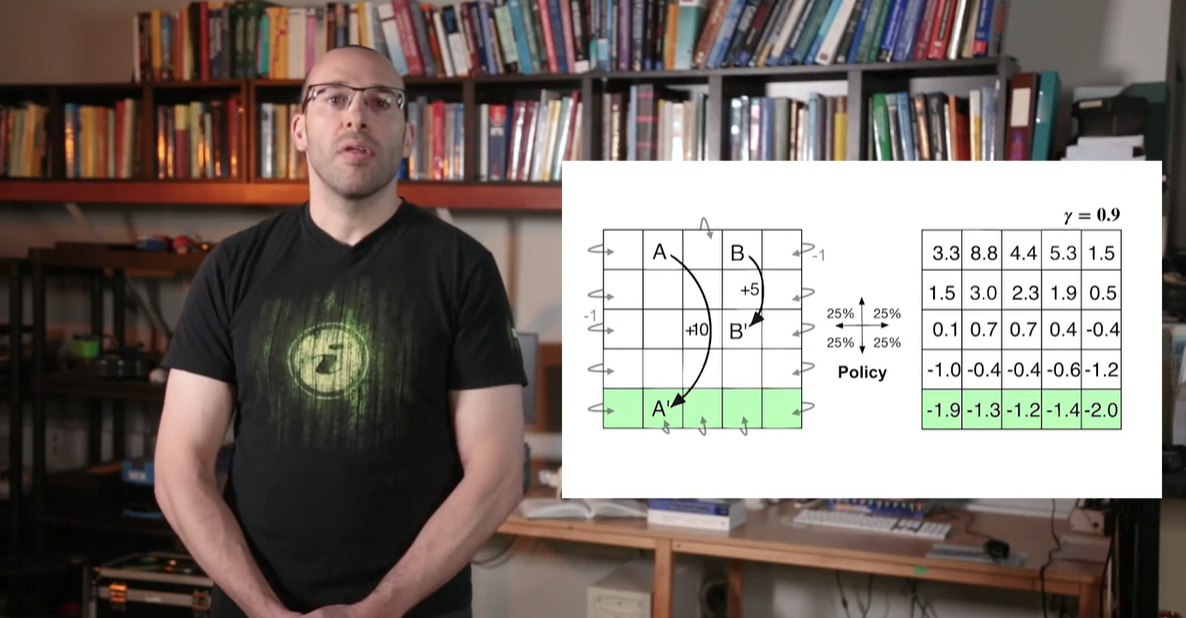
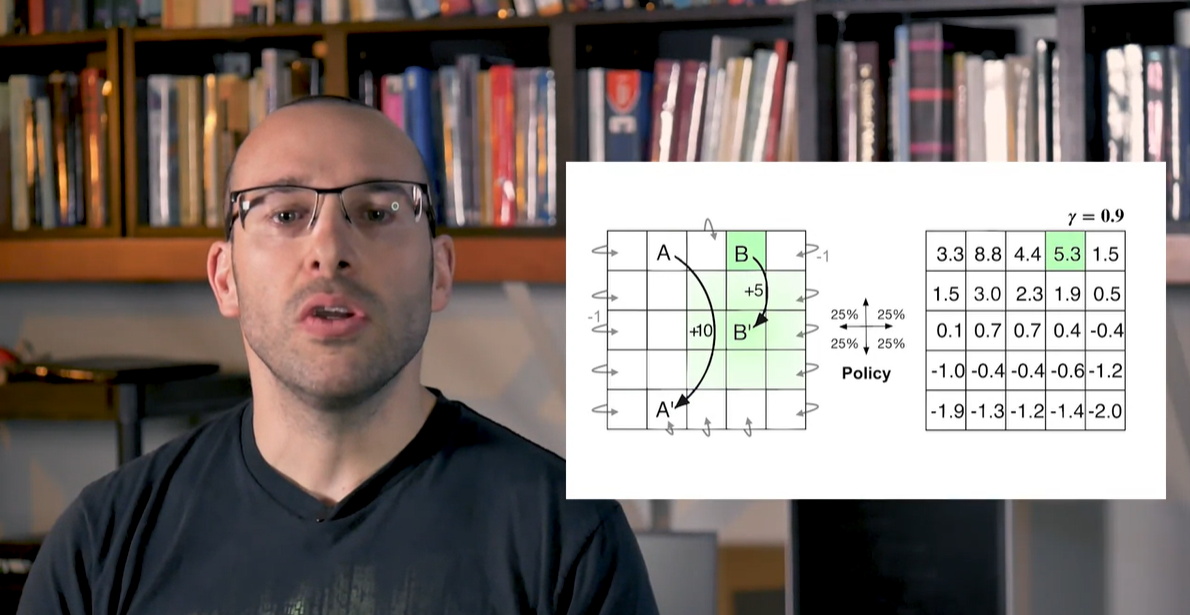
• 아래와 같은 board판이 있고, 상태 A와 B 그리고 reward가 주어진다고 해보자.

  • A에서 A'로 이어지는 구간 이후, 맨 아래 행의 values를 보면 음수 값을 가진다는 것을 알 수 있다.

    • 이는 당장 A'으로 향하는 움직임을 택해 +10의 reward를 얻었음에도, board를 벗어나는 경우의 수로 인한 - reward를 많이 받있기 때문으로 해석할 수 있다.

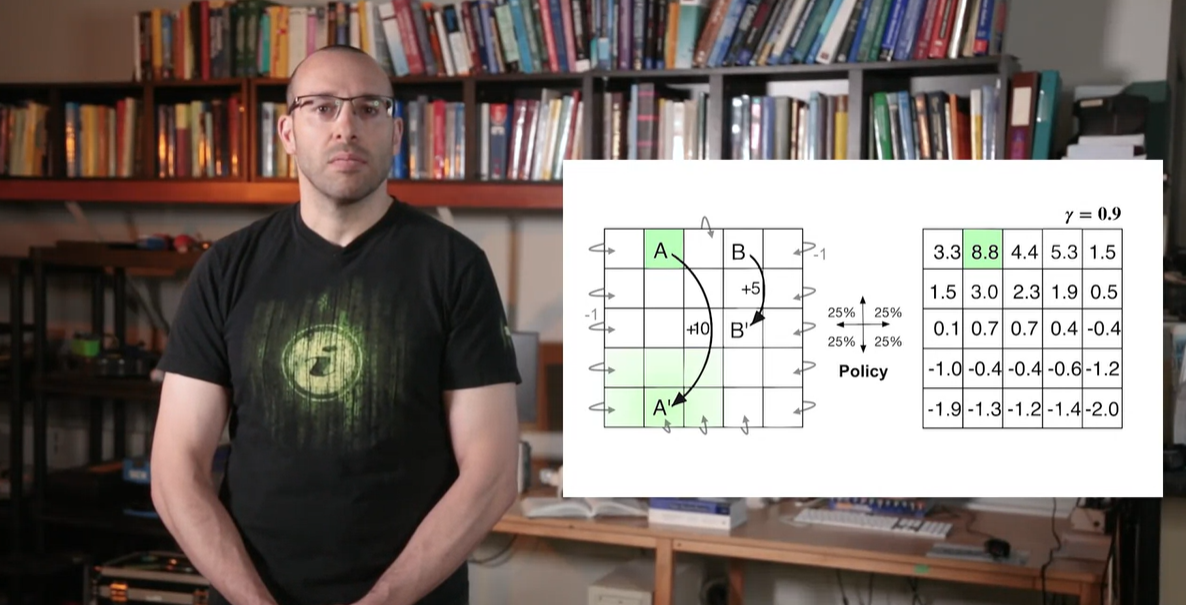
• 반면 시작 지점 A에서의 value는 높은 편이나 reward +10에 비해 작다.

  • 그 이유는 board를 벗어나는 경우의 수로 인한 감쇠 효과 때문이라고 볼 수 있다.

• 그러나 B 지점에서의 value는 reward +5보다 높은 값을 가질 수 있다.

  • 이는 transition B'의 위치가 board의 중앙을 향해 매우 안전한 value를 유지할 수 있기 때문이라고 해석할 수 있다.

• Summary

  • State-value function은 특정 policy를 따르는 state로부터 얻을 수 있는 reward의 전체 기댓값이다.
  • Action-value function은 특정 policy를 따르는 특정 action을 취했을 때의 state로부터 얻을 수 있는 reward의 전체 기댓값이다.

Bellman Equations

Bellman Equation Derivation

• Bellman Equation을 유도해보자.

• 이번 강의에서는 state-value function과 action-value function에서의 bellman equantion을 유도해보고, 현재와 미래 가치와의 관련성을 알아볼 예정이다.

• State-value function은 $v_{\pi}(s) \doteq \mathbb E_{\pi}[G_t|S_t=s]$로 정의했다.

  • $G_t$는 현재 reward $R_{t+1}$과 $\gamma G_{t+1}$의 합으로 분해되며 전체 expectation을 전개하면 다음과 같다.

    • $v_{\pi}(s) \doteq \displaystyle \sum_{a} \pi(a|s) \sum_{s'}\sum_{r} p(s',r|s,a)[r + \gamma \mathbb E_{\pi}[G_{t+1}|S_{t+1} = s']]$

      • $p(s',r|s,a)$는 Markov Process probablity를 나타낸다.

• $\mathbb E_{\pi}[G_{t+1}|S_{t+1} = s']$는 그 다음 state인 $s'$에서 기대할 수 있는 미래 가치($v_{\pi}(s')$)를 의미한다.

  • $v_{\pi}(s) \doteq \displaystyle \sum_{a} \pi(a|s) \sum_{s'}\sum_{r} p(s',r|s,a)[r + \gamma v_{\pi}(s')]$

• Action-value function은 $q_{\pi}(s,a) \doteq \mathbb E_{\pi}[G_t|S_t=s, A_t=a]$로 전개됐었다.

  • 이는 $\displaystyle \sum_{s'} \sum_{r} p(s',r|s,a)[r+\gamma \mathbb E_{\pi}[G_{t+1}|S_{t+1} = s']]$로 전개된다.

    • 이 때 $\mathbb E_{\pi}[G_{t+1}|S_{t+1} = s']$는 action distribution(policy) $\pi$와 value $v(s')$ 곱으로 전개할 수 있다.

      • $\displaystyle \sum_{a'} \pi(a'|s') \mathbb E_{\pi}[G_{t+1}|S_{t+1}=s', A_{t+1}=a']$는 다시 $q_{\pi}(s',a')$이다.

• Summary

  • Current time step에서의 state/action values는 미래 가치의 reculsive한 결과를 내포한다는 것을 알 수 있다.

Why Bellman Equations?

• Bellman Equation이 왜 쓰이는 걸까?

• 이번 강의에서는 bellman equation을 사용하여 실제 computing하는 과정에 대해 알아볼 것이다.

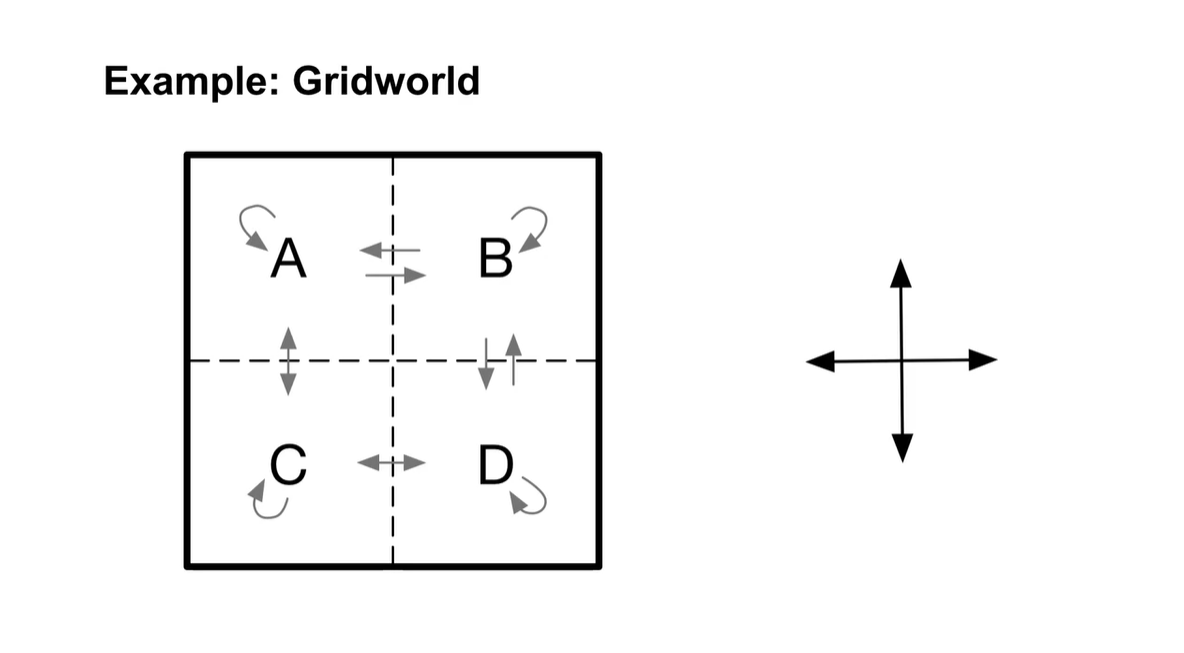
• 아래와 같은 Grid 판에 state가 A, B, C, D로 주어지고, 각 state에서의 전이 확률이 고려된 경우의 수가 화살표로 그려졌다고 하자.

  • Action을 취할 수 있는 경우의 수는 동서남북 네 가지가 가능하다.

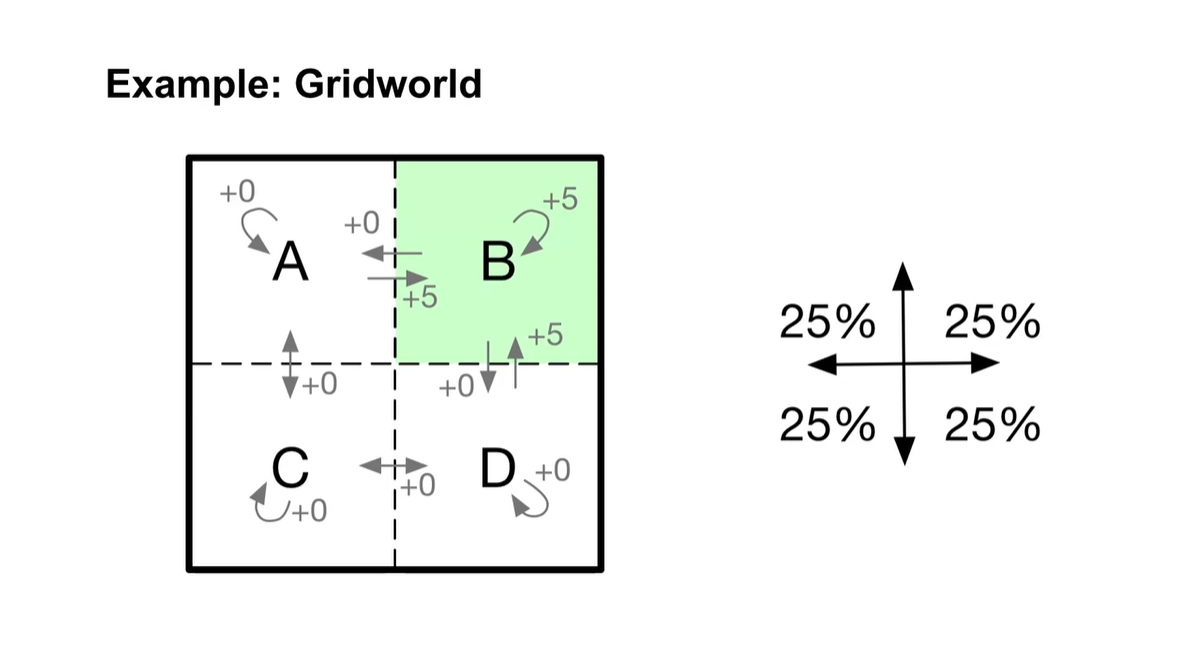
• 다른 state에서는 보상이 없지만 B state에서의 보상이 +5로 주어지는 환경(environment)이라고 가정하자.

  • 취할 수 있는 action은 네 가지이며 각 확률은 동일하게 1/4이다.

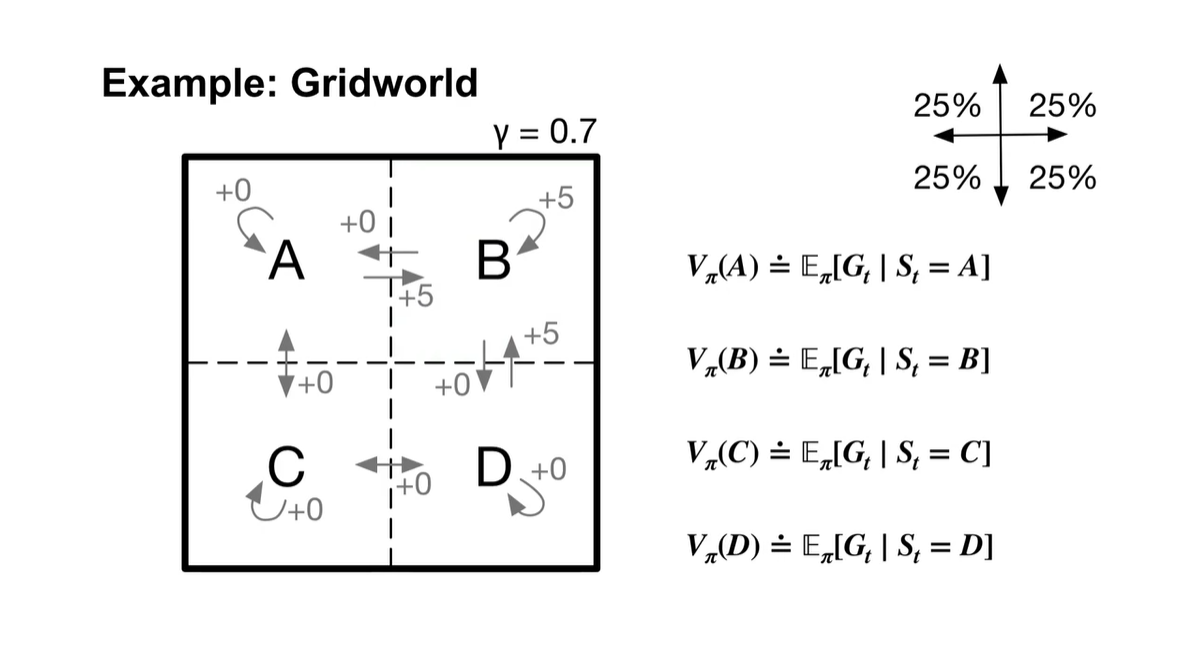
• $\gamma$는 0.7로 설정하고, state-value function은 각 state마다 구한다.

  • S가 A일 때, B일 때, C일 때, D일 때 모두의 미래 가치를 계산할 것이다.

• State A에서 시작한 $v_{\pi}(A)$는 $\displaystyle \sum_{a} \pi(a|A)(r+0.7v_{\pi}(s'))$를 계산하면 된다.

  • A에서 B로가는 state, A에서 C로 가는 state, A에서 A로 가는 state가 전체 경우의 수라는 사실은 Markov Process probaility를 고려하여 얻어진다.

    • 따라서 policy(action distribution probability)인 1/4과 각 전이 상태에서의 value의 평균치를 계산한다.

• 이렇게 모든 state에서의 value를 구하면 다음과 같이 전개된다.

• Scalar 값으로 표현하면 아래와 같다.

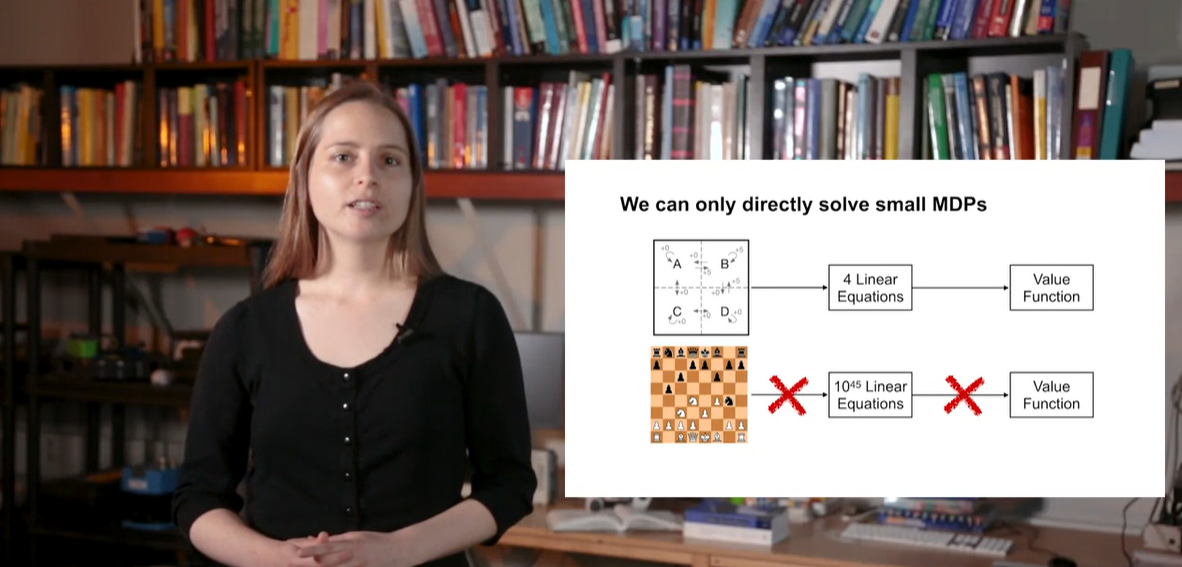
• 위와 같은 small MDP는 linear한 solution으로 해결이 가능하다.

  • 그러나 chess game과 같은 상황에서는 매우 많은 경우의 수를 고려해야 하기 때문에 컴퓨터로 시뮬레이션 하여 value를 계산해야만 한다.

• Summary

Optimality (Optimal Policies & Value Functions)

Optimal Policies

• Optimal policy를 정의해보자.

• 이번 강의에서는 optimal policy의 개념과 모든 state에서 optimal policy를 선택하는 것이 왜 좋은지에 대해 이해해보려 한다.

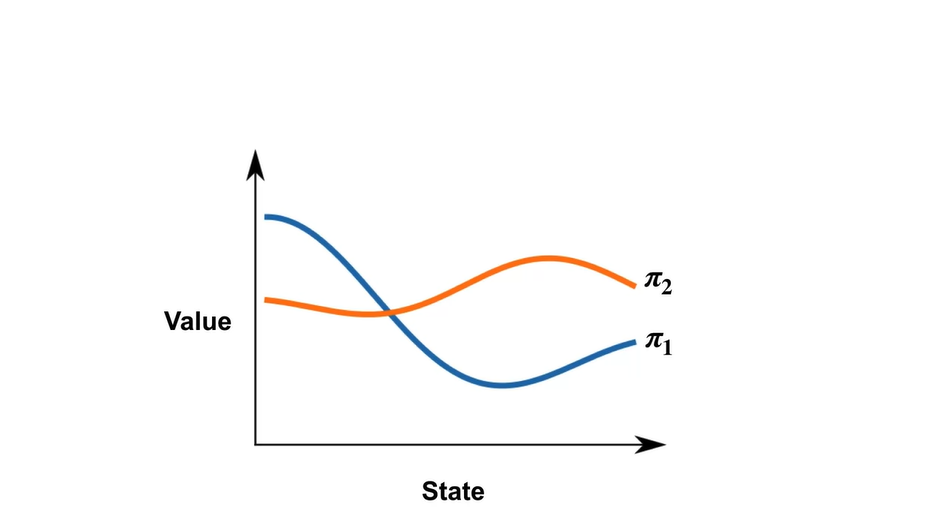
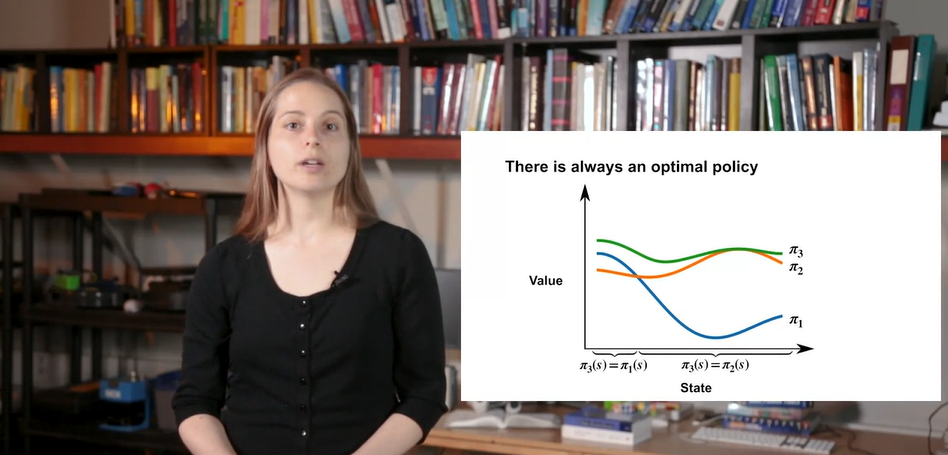
• 아래와 같은 두 policies $\pi_1$과 $\pi_2$를 비교해보자.

  • 가까운 states에서의 value가 더 큰 $\pi_1$과 먼 states에서의 value가 더 큰 $\pi_2$를 보고서는 둘 중 어떤 policy가 더 좋은지 판단하기 어렵다.

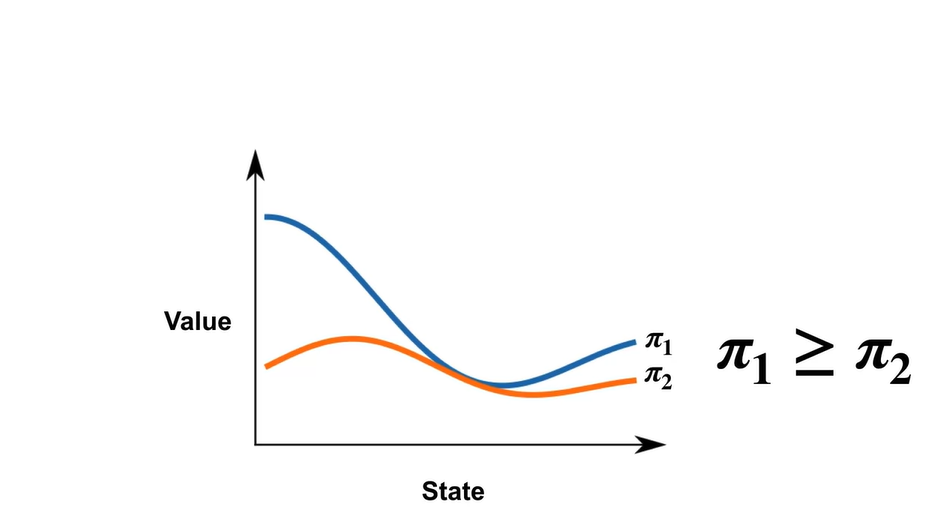
• 만일 $\pi_1$이 항상 $\pi_2$보다 크거나 같다면 $\pi_1$이 더 좋은 정책이라고 말할 수 있다.

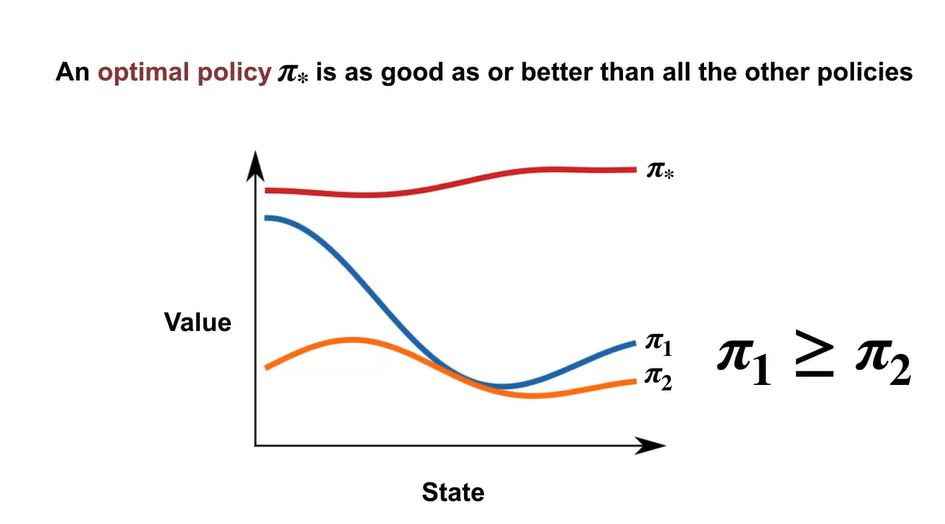
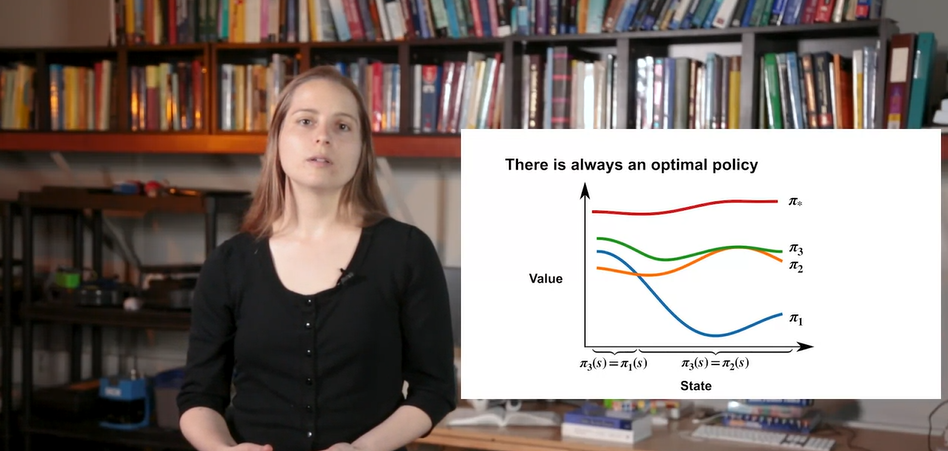
• Optimal policy란 다른 모든 policy와 비교하였을 때 모든 states에서 항상 best인 policy를 의미한다.

  • 아래 그래프에서는 $\pi_{*}$가 optimal policy다.

• 교차점을 기준으로 $\pi_1$과 $\pi_2$의 policy를 비교하여, $\pi_1$이 큰 states에서는 $\pi_1$을 채택하고 $\pi_2$가 큰 states에서는 $\pi_2$를 채택한 policy를 $\pi_3$라고 하자.

  • 즉, 모든 states에서의 best policy를 매번 선택한다면 optimal policy는 적어도 하나 이상 존재한다고 결론지을 수 있다!

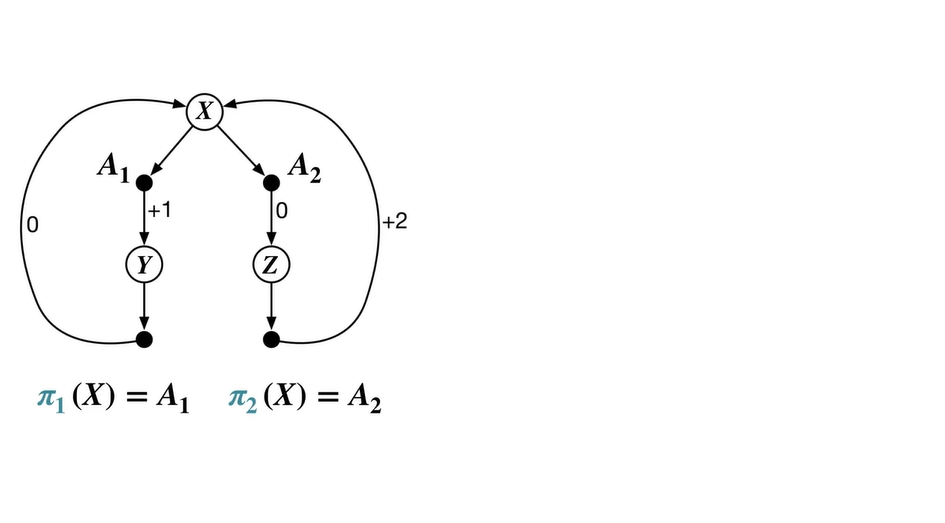
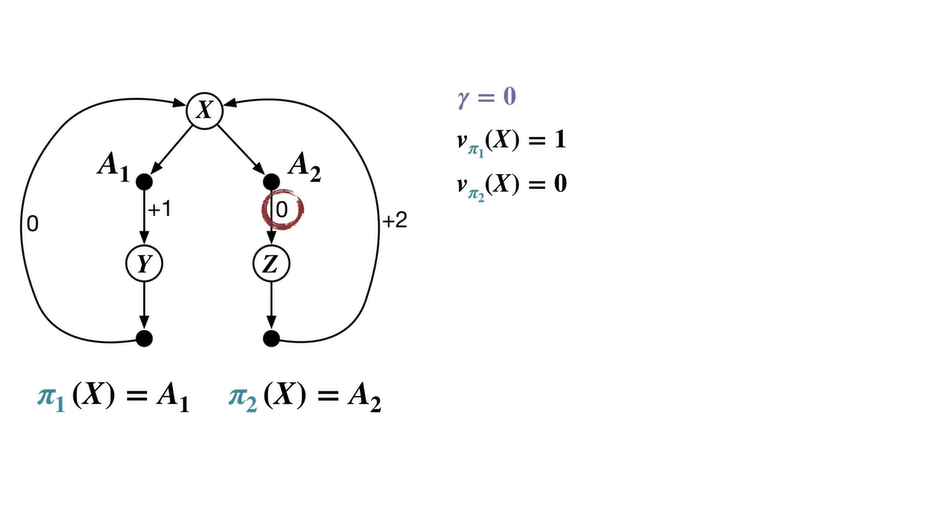
• 아래와 같은 MDP process가 존재한다고 가정해보자.

  • $X$ state에서 시작하여 $A_1$과 $A_2$로 넘어갈 수 있는 system이라면 $\pi_1(X) = A_1$, $\pi_2(X) = A_2$다.

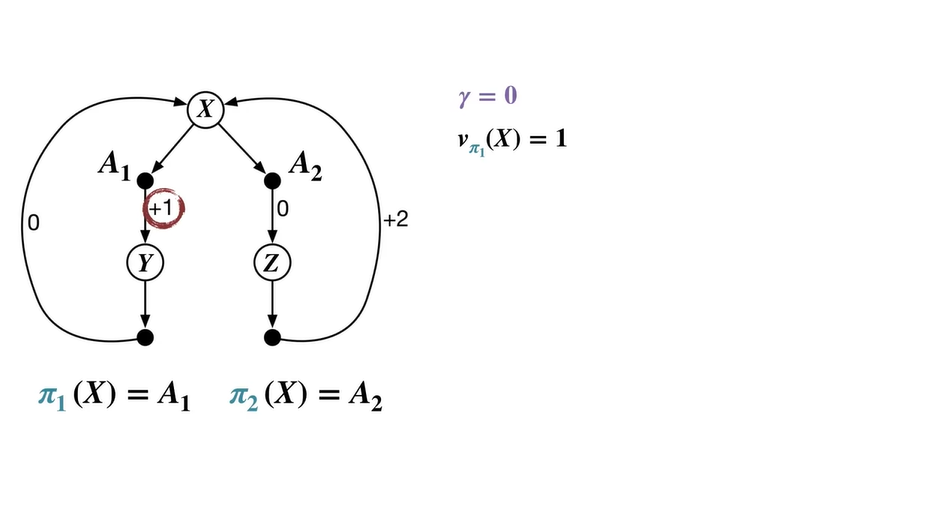
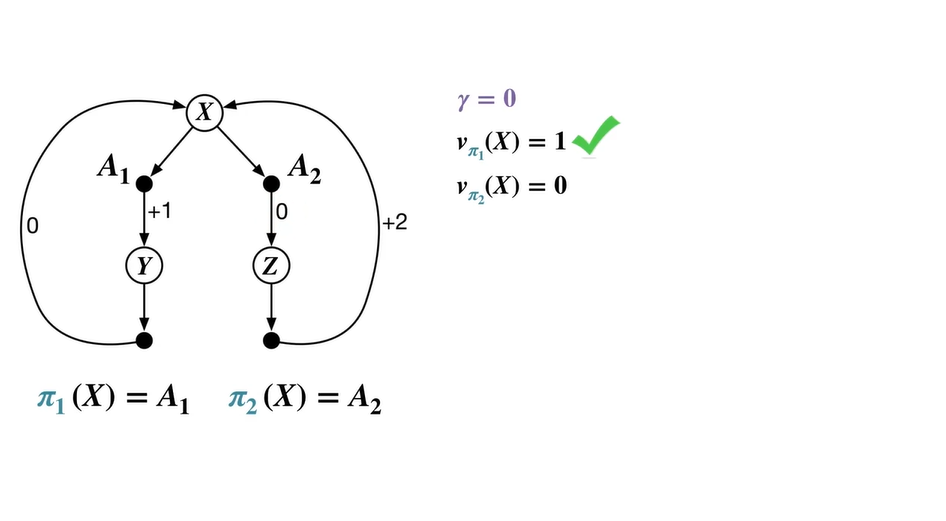
• $\gamma = 0$이면 미래 가치를 전혀 고려하지 않고 당장의 reward만을 계산한다.

  • 따라서 $v_{\pi_1}(X) = +1$, $v_{\pi_1}(X) = 0$이다.

    • 이 때의 optimal value는 $\pi_1$을 따르는 $v_{\pi_1}(X) = 1$이며 $\pi_1$을 optimal policy로 채택한다.

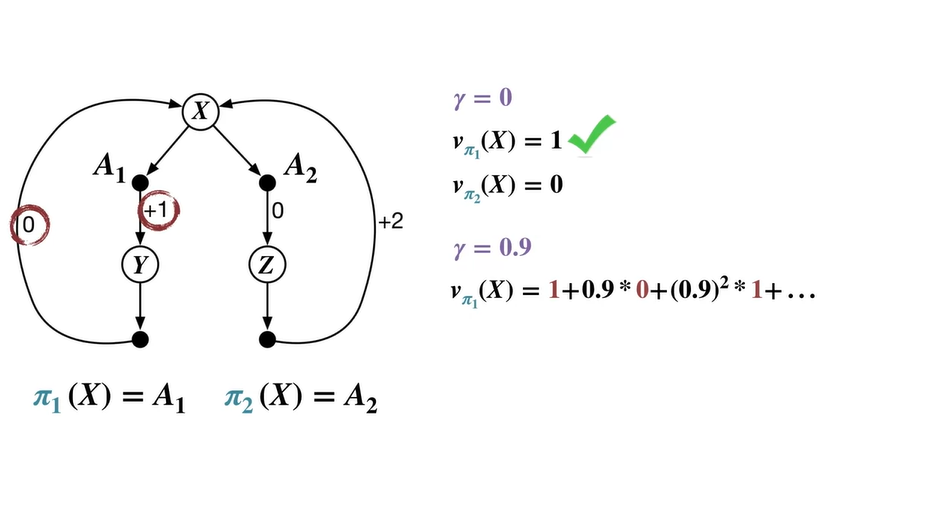
• $\gamma = 0.9$면 미래 가치를 감쇄하여 더한 reward의 평균을 계산한다.

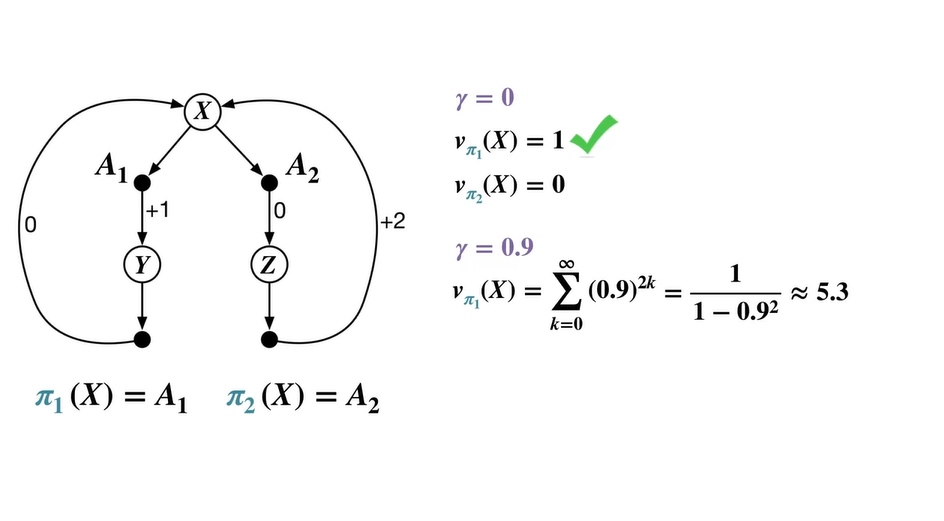
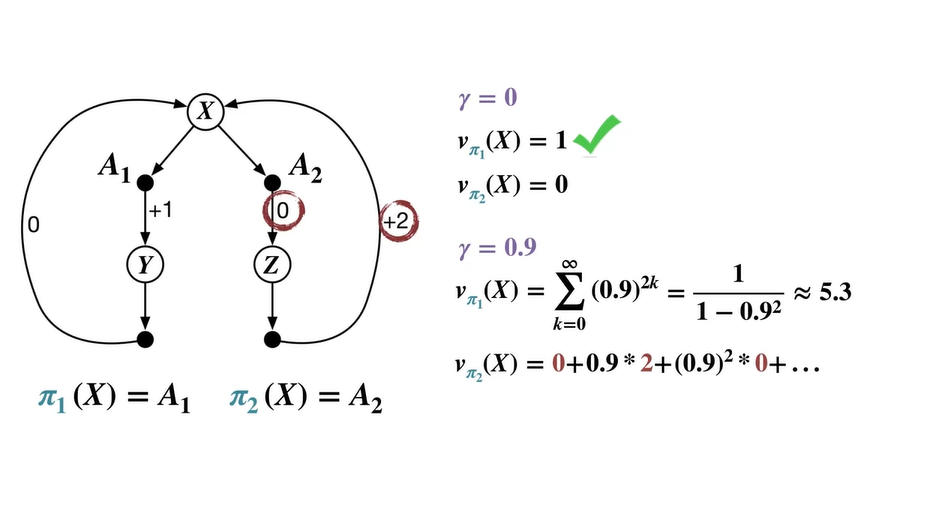
  • Policy $\pi_1$을 따르는 value는 1 → 0 → 1 → 0, ...의 연쇄에 $\gamma$를 제곱배하여 더한 급수로 표현된다.

    • Geometric function으로 나타내면 $\displaystyle \sum_{k=0}^{\infin}(0.9)^{2k} = \frac{1}{1-0.9^2} \approx 5.3$이다.

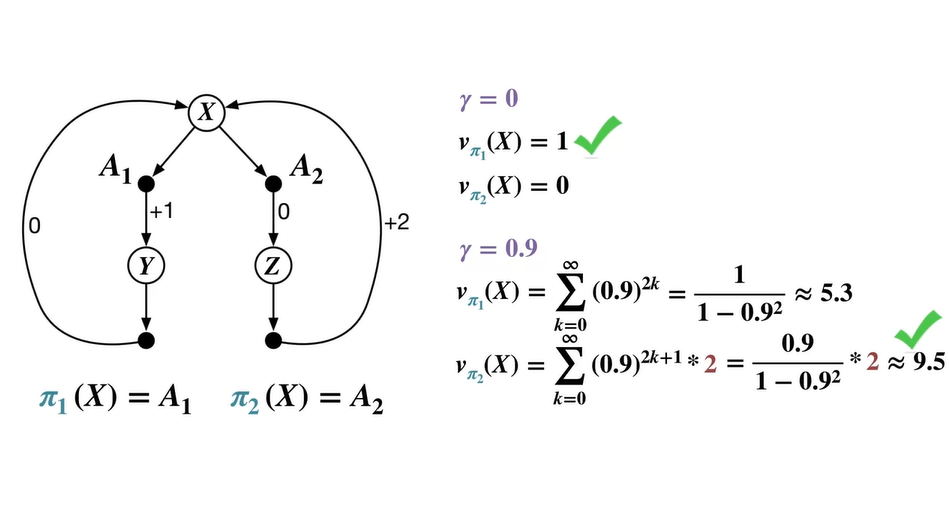
• Policy $\pi_2$를 따르는 value는 0 → 2 → 0 → 2, ...의 연쇄에 $\gamma$를 제곱배하여 더한 급수로 표현된다.

  • Geometric function으로 구하면 $\displaystyle \sum_{k=0}^{\infin}(0.9)^{2k+1} * 2 = \frac{1}{1-0.9^2} * 2 \approx 9.5$이다.

    • 이 때의 optimal value는 $\pi_2$을 따르는 $v_{\pi_2}(X)$이며 $\pi_2$을 optimal policy로 채택한다.

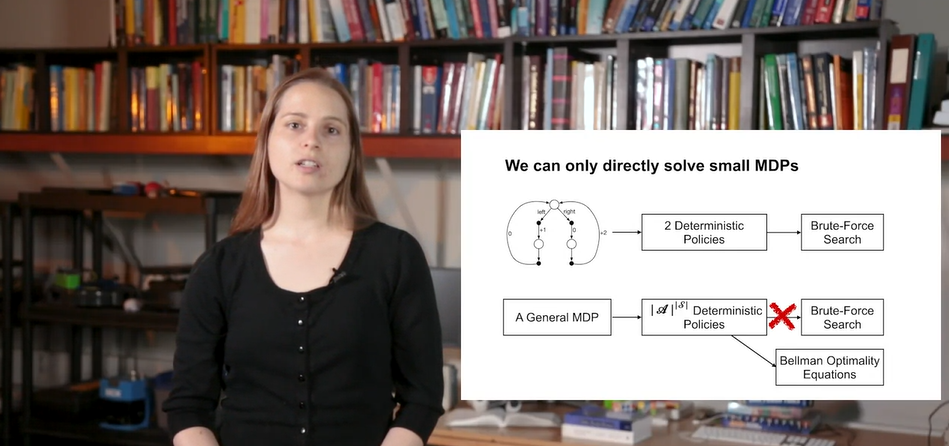
• 위 예제는 매우 간단한 MDP process였기 때문에 Brute-force 알고리즘으로 optimal value&policy를 찾아낼 수 있었다.

  • 일반적인 MDP는 수많은 states의 연속이기 때문에 Bellman Optimality Equations로 policy를 채택하여야 한다.

Optimal value functions

• Optimal value function은 어떻게 구해질까?

• 이번 강의에서는 state-value function과 action-value function의 Bellman optimality equations를 유도해보자.

• 모든 states에서 policy $\pi_1$을 따르는 value가 항상 크다면 $\pi_1$이 $\pi_2$보다 크다고 말할 수 있었다.

  • 따라서 optimal state-value $v_*$는 모든 states에서의 optimal value를 가리킨다.
  • 마찬가지로 optimal action-value $q_*$는 모든 states와 취한 actions에서의 optimal value를 가리킨다.

• $v_*$는 policy $\pi_*$가 결정되었을 때의 value를 계산하여 구할 수 있다.

  • 따라서 현재 state에서 action이 max(optimal)한 value를 계산하여 나타낸 것이 바로 Bellman Optimality Equation for $v_*$다.

• $q_*$는 해당 state에서 action이 이미 결정된 상태에서, policy $\pi_*$가 결정되었을 때의 value를 계산하여 구할 수 있다.

  • 따라서 현재 state에서 action'이 max(optimal)한 value를 계산하여 나타낸 것이 바로 Bellman Optimality Equation for $q_*$다.

• 기존 Bellman Equation은 linear equation으로 풀 수 있었으나 optimality가 포함되면 non-linear system이 되어 linear equation으로 풀 수 없다.

  • 왜냐하면 기존 Bellman Equation으로는 $\pi_*$를 알아낼 수 없기 때문이다.

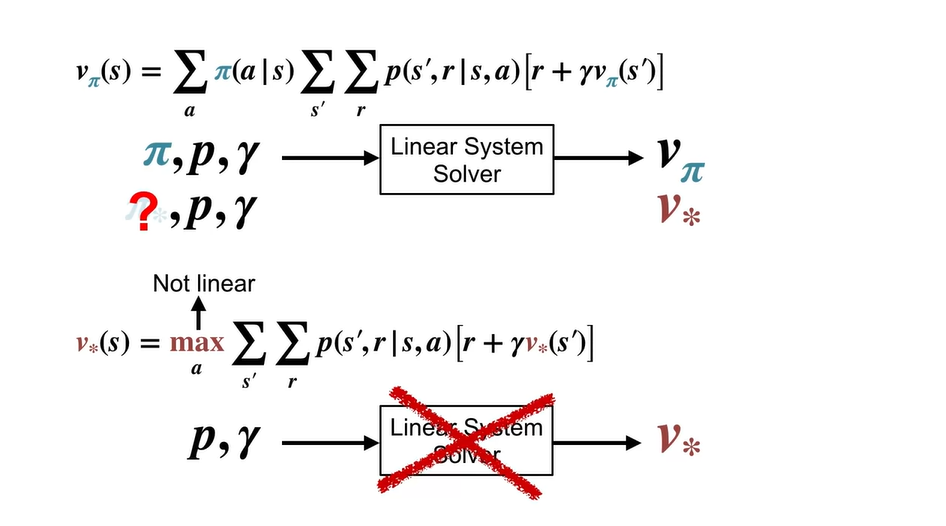
• Summary

Using Optimal Value Functions to Get Optimal Policies

• Optimal Value Functions을 이용하여 Optimal Policies를 선택해보자.

• 이번 강의에서는 optimal value와 optimal policy간의 관계를 정의할 것이다.

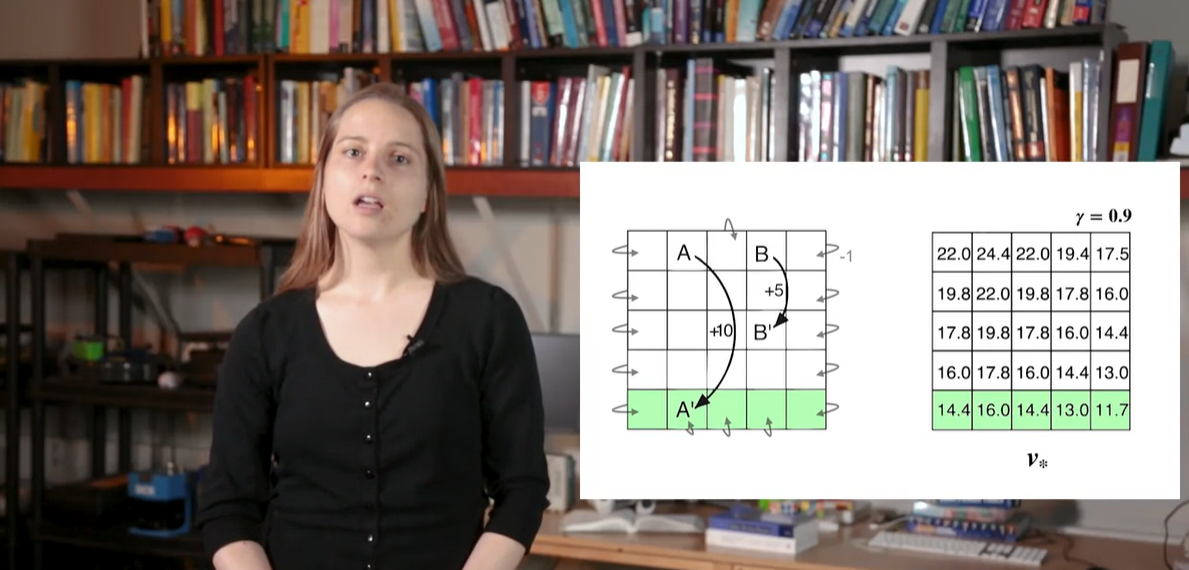
• 이전에 다뤘던 예제에서의 board values가 오른쪽과 같이 계산되었다고 하자.

  • 이전에는 맨 밑의 row가 -값의 reward를 받았으나, optimal value로 계산한 결과 다소 높은 +값의 value를 획득했다는 것을 알 수 있다.

    • 마찬가지로 initial state A의 value 또한 24로, 다소 높은 값을 가진다.

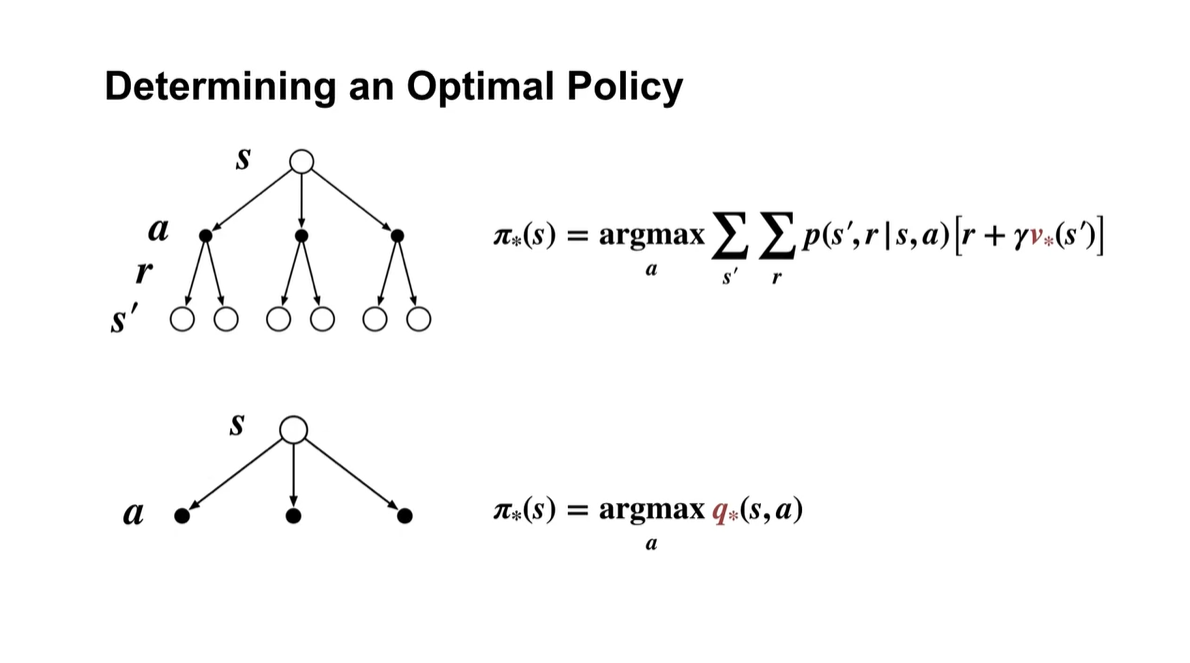
• Optimal Policy를 결정하는 것은 optimal value일 때의 argmax로 알 수 있다.

  • 즉, 어떠한 action을 취하였을 때 value가 max값을 가진다면, 해당 action을 선택하는 것이 무엇인지를 알아내는 것(argmax)이 optimal policy인 것이다.

    $v_* (s) = \displaystyle max_{a} \sum_{s'} \sum_{a} p(s', r|s, a)|[r + \gamma v_{*}(s')]$

    $\pi_* (s) = \displaystyle argmax_{a} \sum_{s'} \sum_{a} p(s', r|s, a)|[r + \gamma v_{*}(s')]$

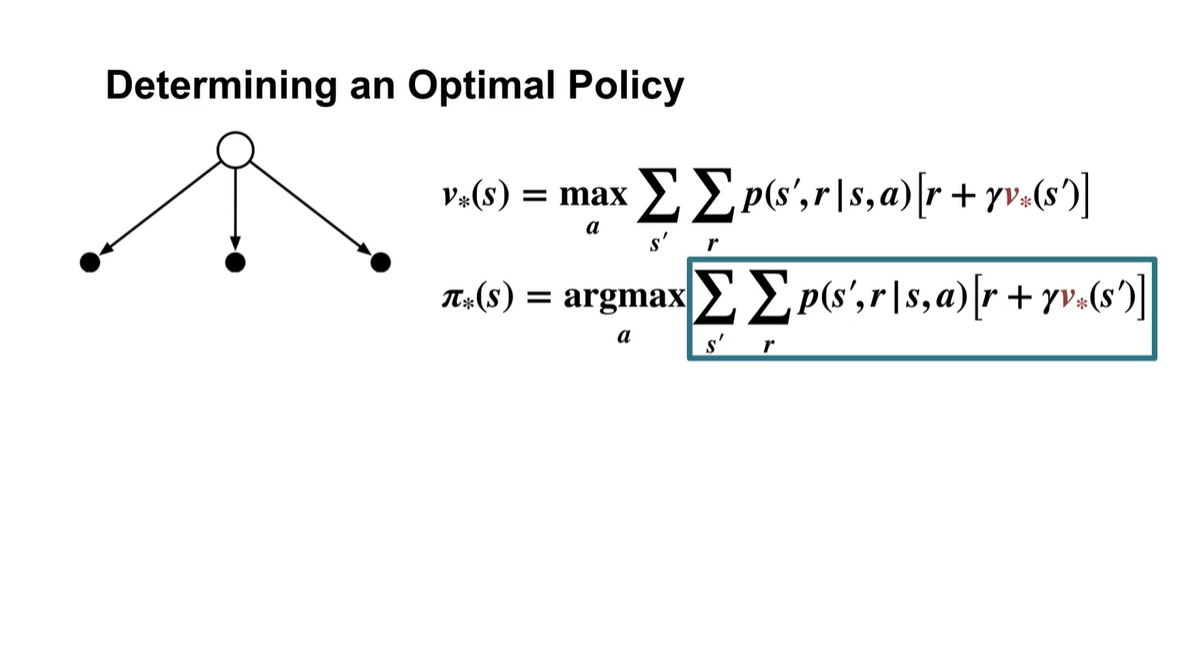
• 아래와 같이 $A_1$, $A_2$, $A_3$의 action을 선택하였을 때 얻어지는 value가 각각 5, 10, 7의 값이라면 $\pi_*$는 $A_2$를 action으로 취하였을 때 얻어지는 value인 것이다.

  • 그리고 그 다음 state에서 얻어지는 최적의 value($v_*(s')$)를 다시 고려한다.

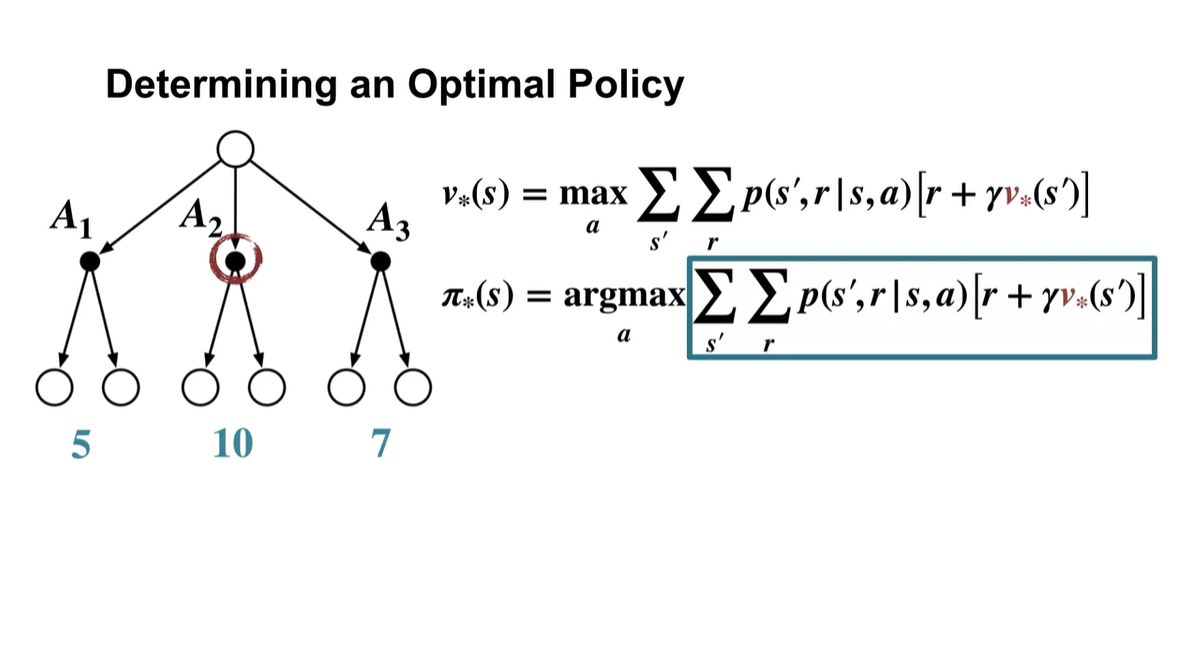
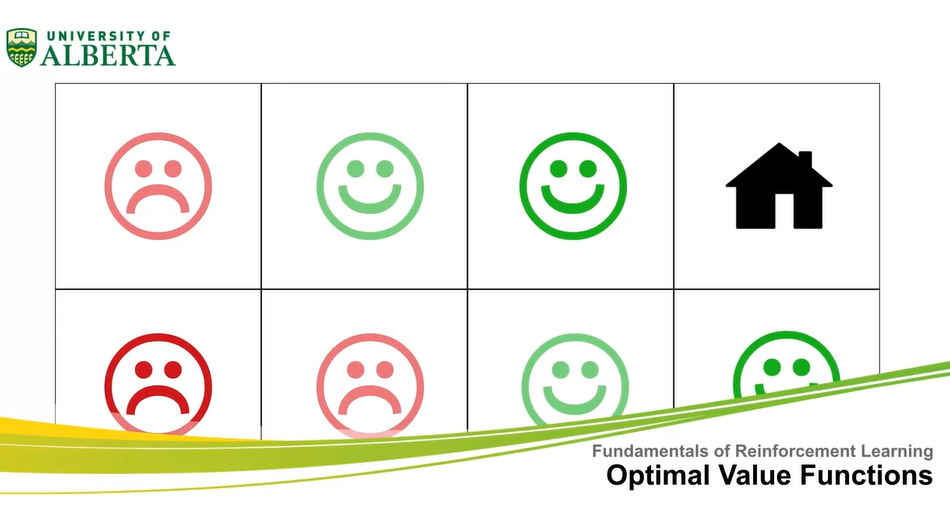
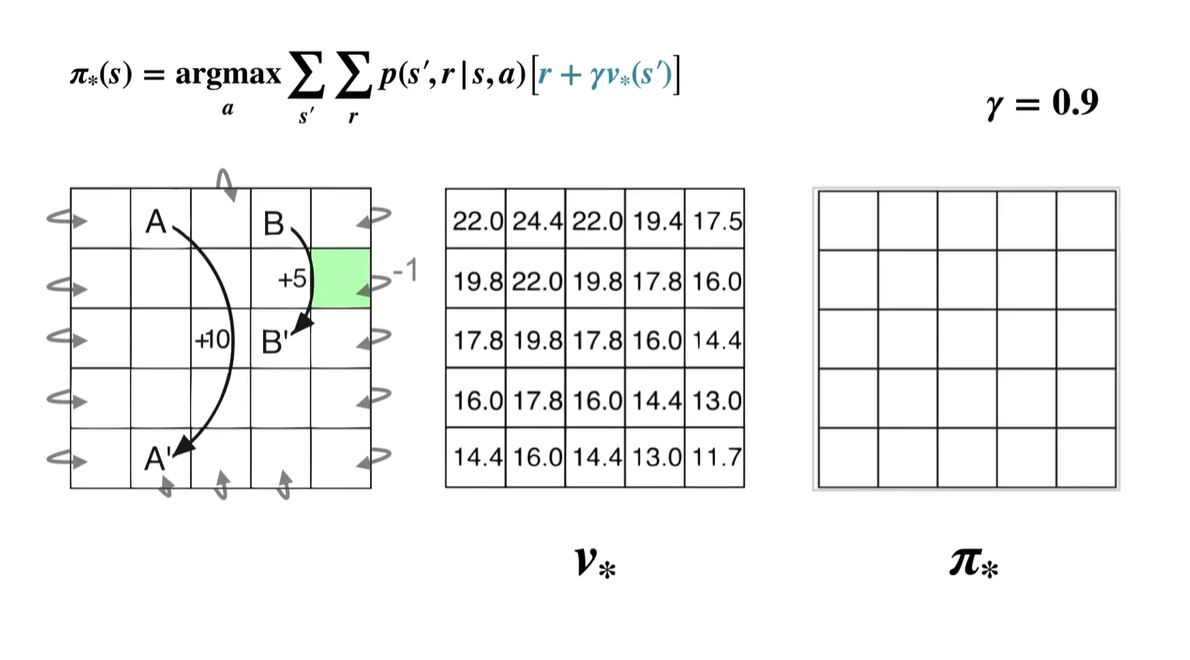
• 만약, 초록색으로 색칠된 부분에서 initial state를 갖게 되었다고 해보자.

  • $\gamma$는 0.9의 감쇠 효과를 가진다.

• 이제 initial state에서 상하좌우로 움직여 각 움직임에서 얻어지는 value를 계산해보자.

  • Up : $0 + 0.9 * 17.5 = 14.0$
  • Right : $-1 + 0.9 * 16.0 = 13.4$
  • Down : $0 + 0.9 * 14.4 = 13.0$
  • Left : $0 + 0.9 * 17.8 = 16.0$

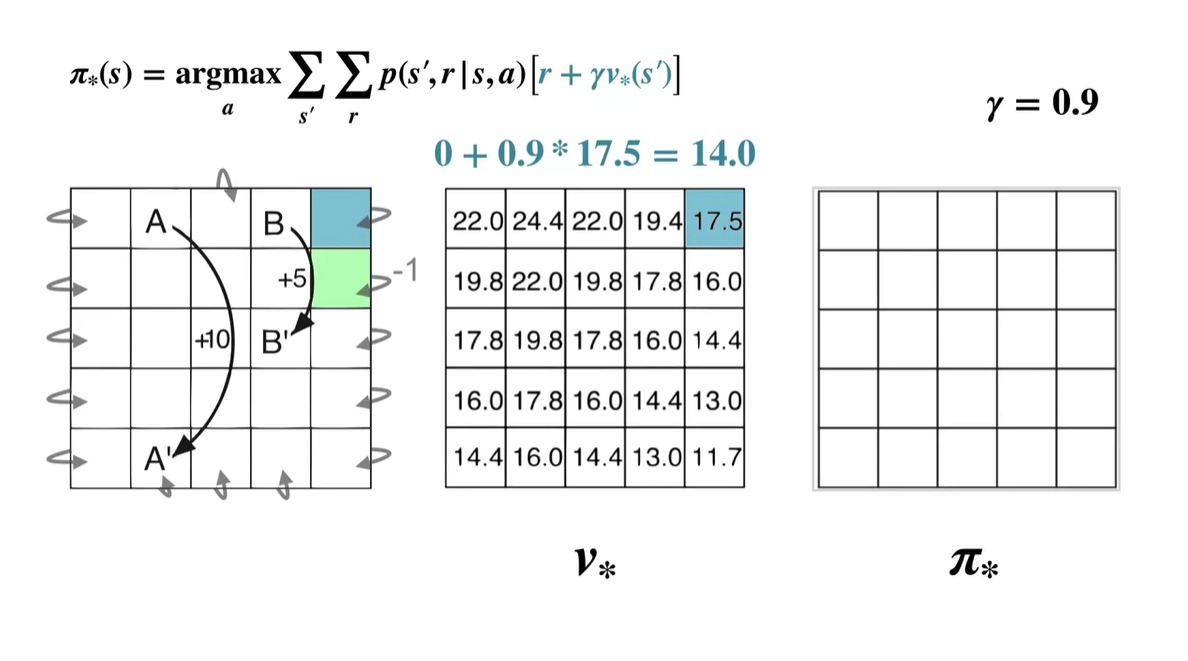
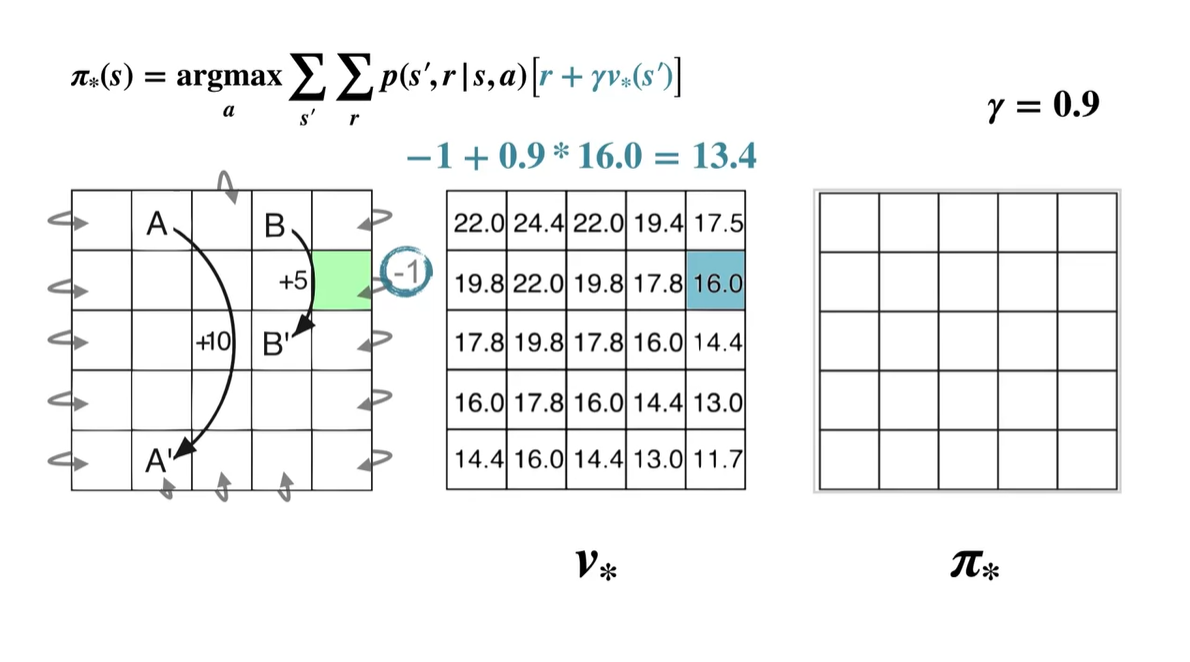
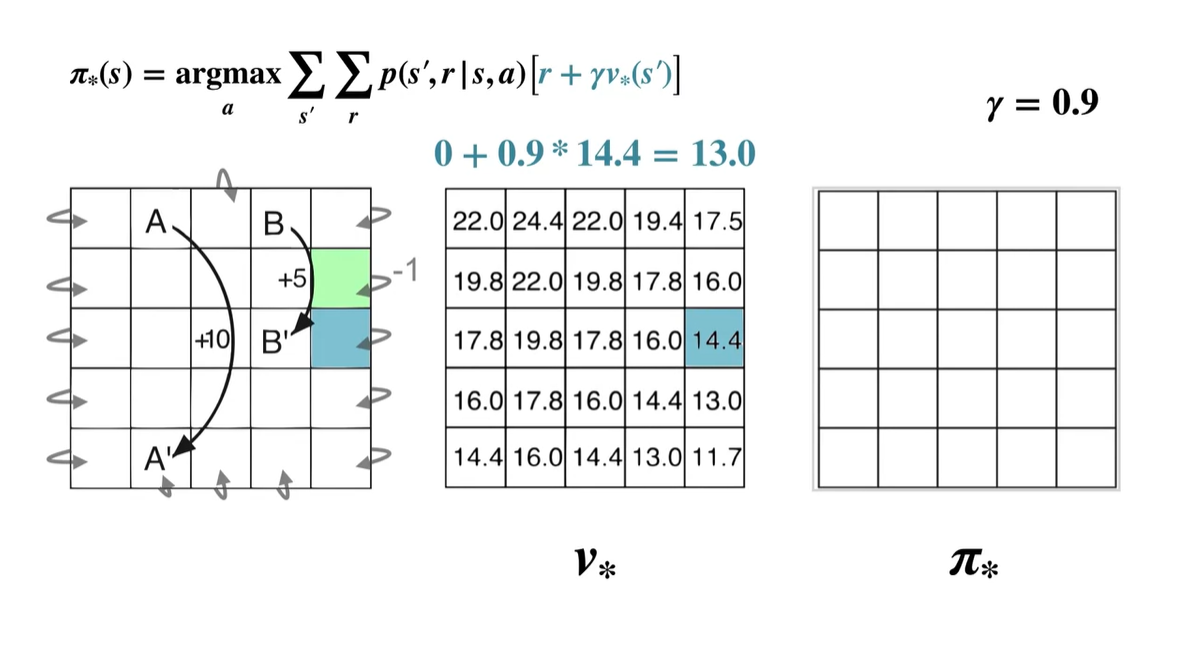
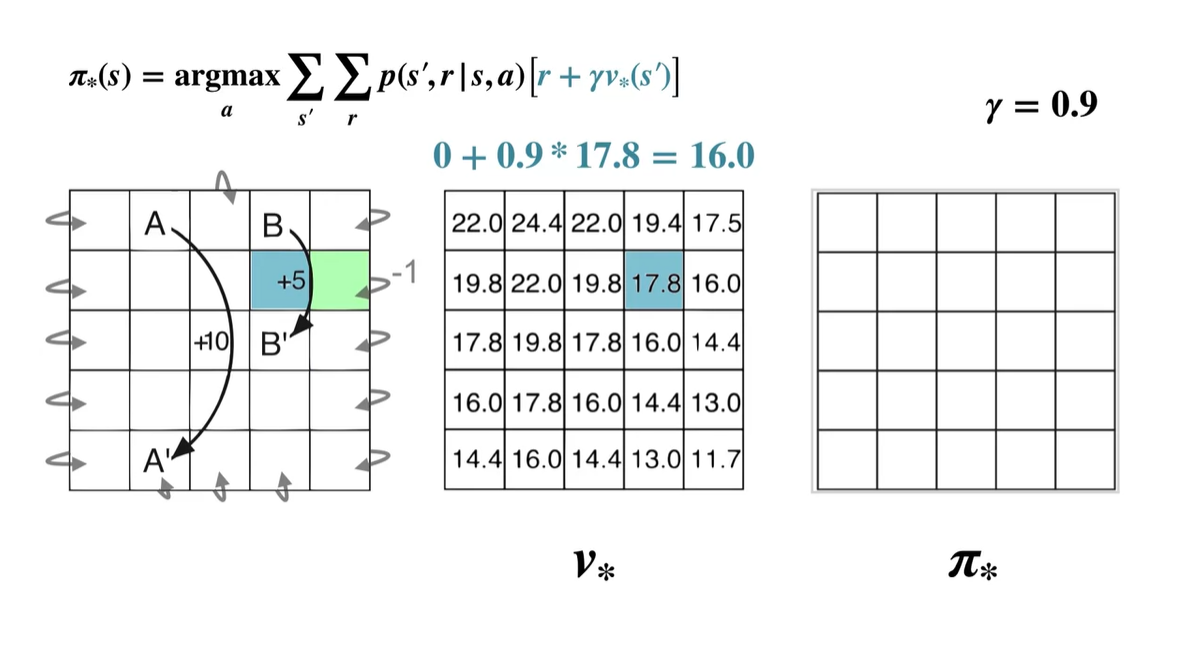
• 계산된 value 중 가장 큰 값을 갖는 policy는 Left이므로 $\pi_*$는 ← 이다.

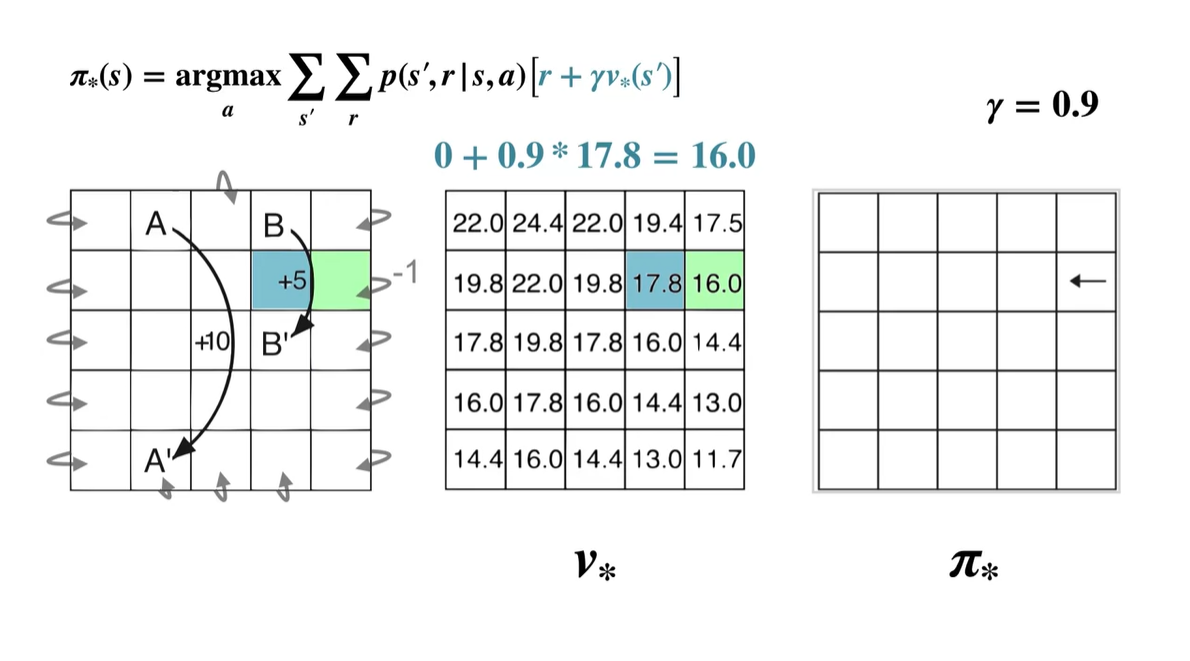
• 이번에는 다른 state에서 계산해보자.

  • 파란색 박스의 value가 모든 action-value 중 가장 크기 때문에 optimal policy $\pi_*$는 Up, Left다.

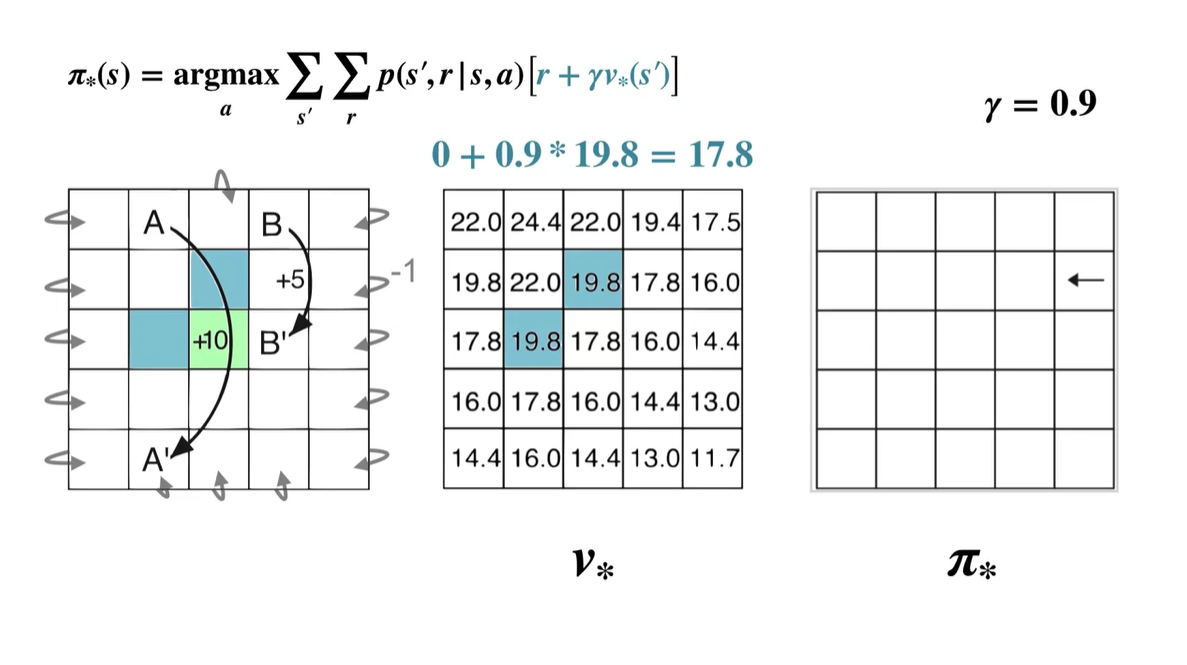
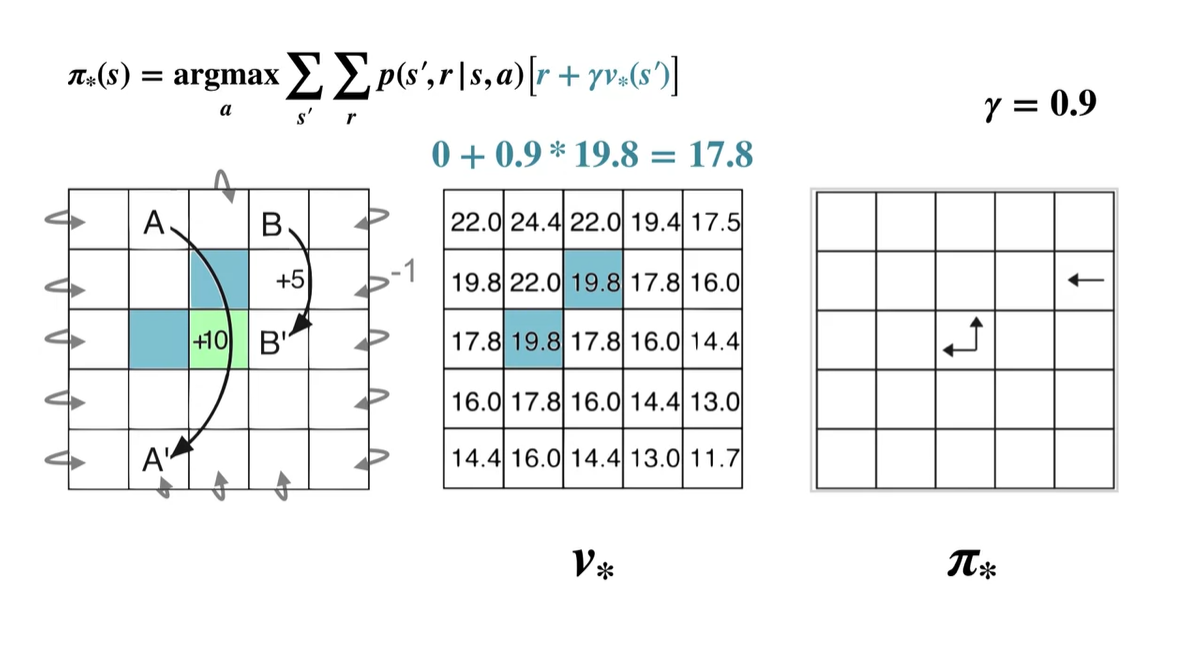
• A state의 경우는 어떤 행동을 취하든지에 상관없이 +10의 reward를 받는 A' state로 전환된다.

  • 따라서 당장의 optimal policy는 Up, Right, Down, Left 경우의 수를 모두 갖는다.

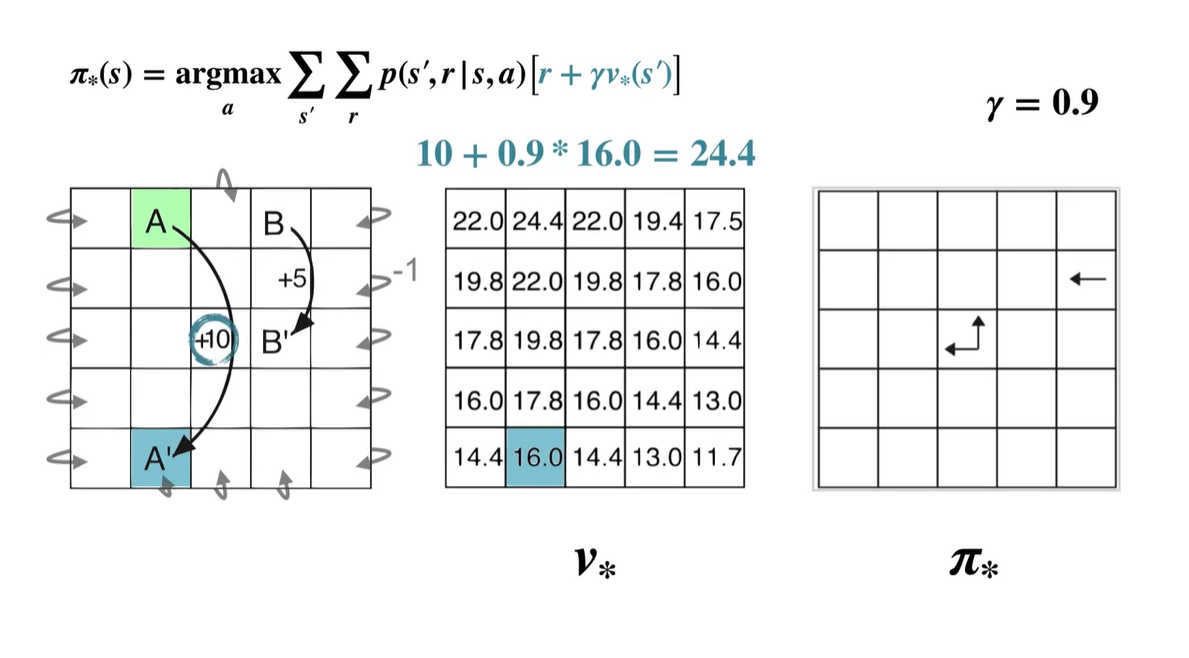
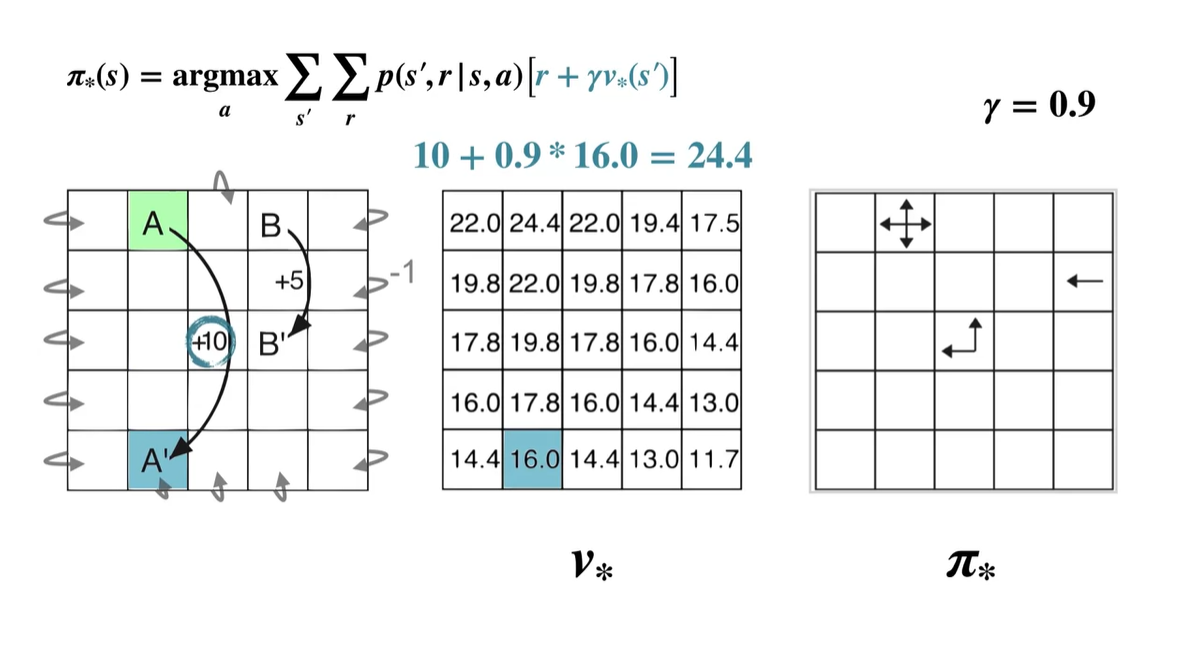
• A state에서의 optimal value는 A' state로 전환되었을 때의 value $v_*$다.

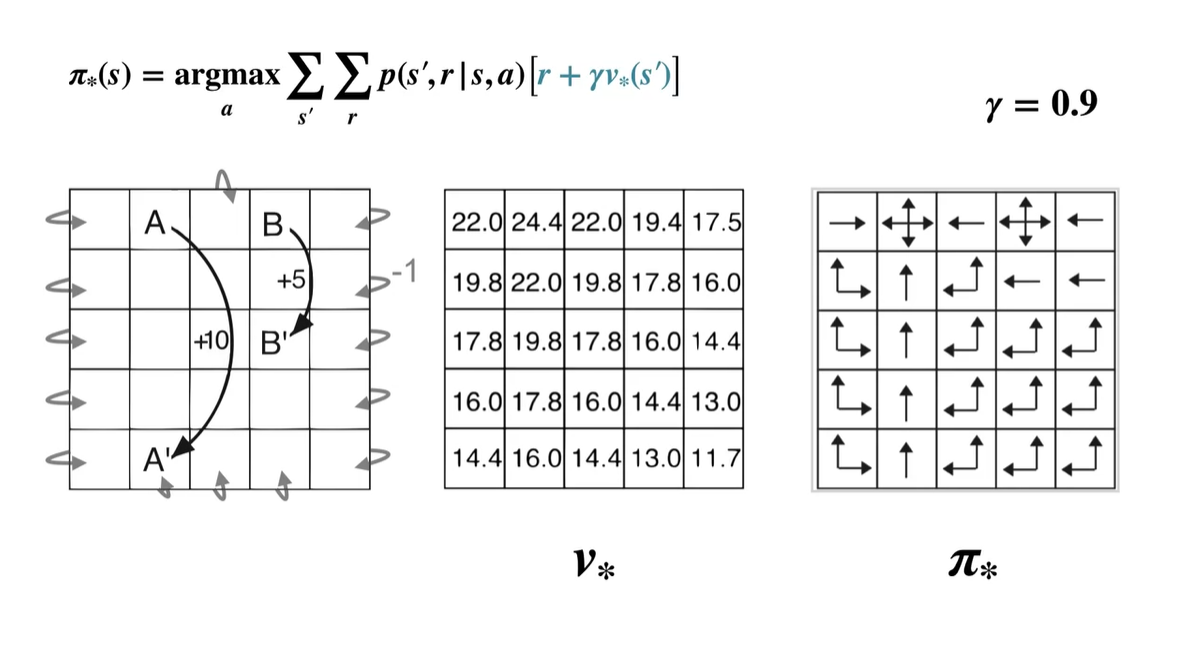
• 이렇게 모든 state에서의 optimal policy와 optimal value를 계산한 결과는 아래와 같다.

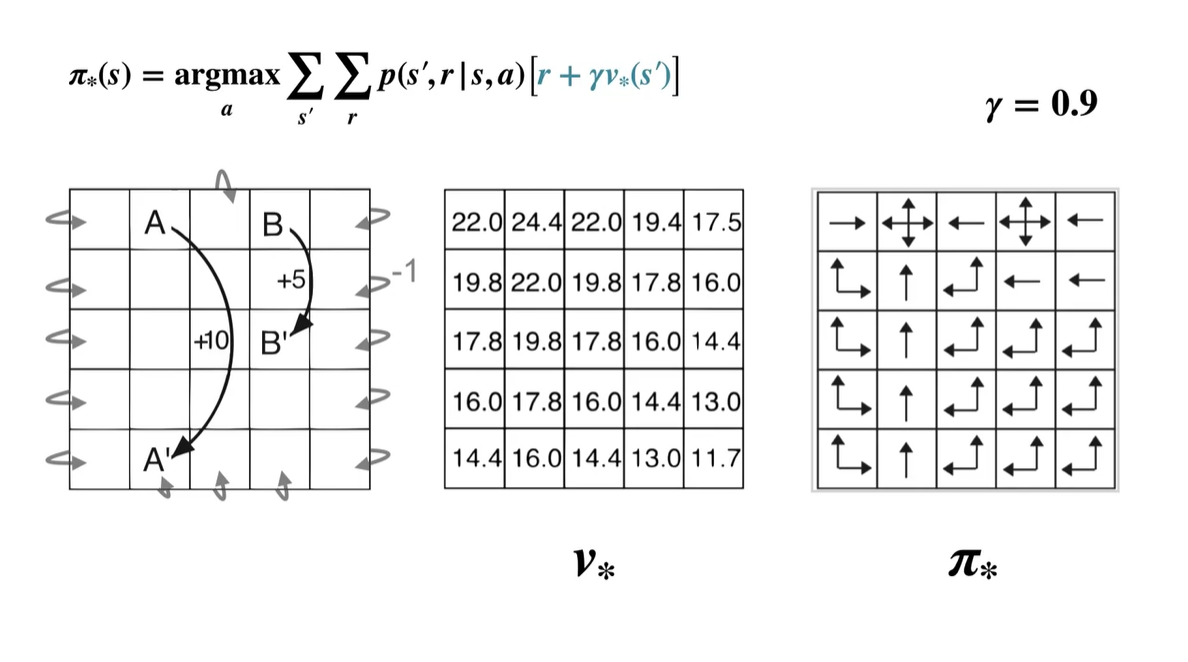
• Optimal policy의 결정은 어떠한 action을 취했을 때의 value가 가장 높은(optimal value를 갖는) 선택지를 찾아내는 것이다.

  • 따라서 $\pi_*(s) = \displaystyle argmax_{a} q_*(s, a)$로 정의한다.

• Summary

---

• 출처 : [Coursera] Reinforcement Learning Specialization