벡터와 공간 | 영공간

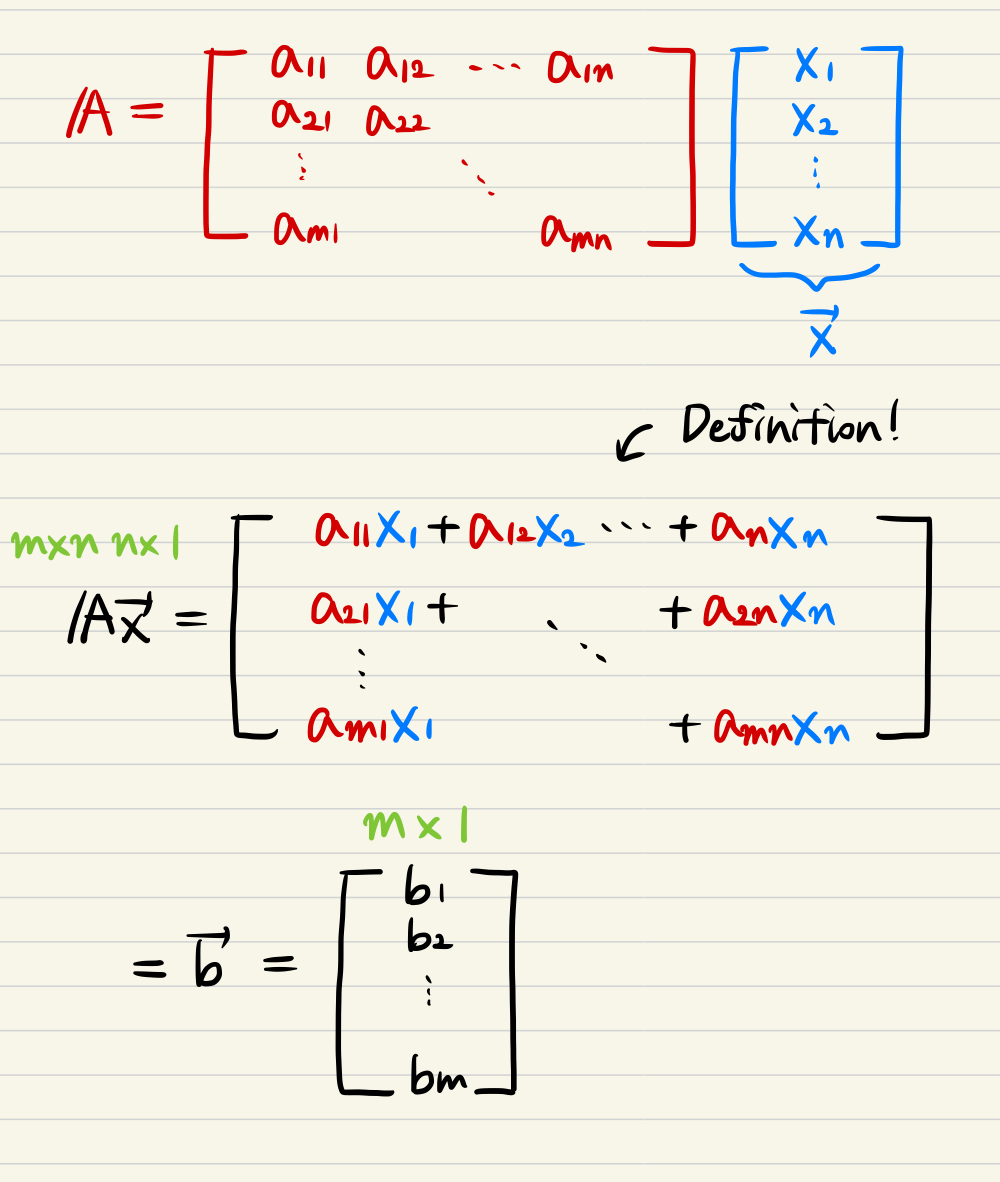
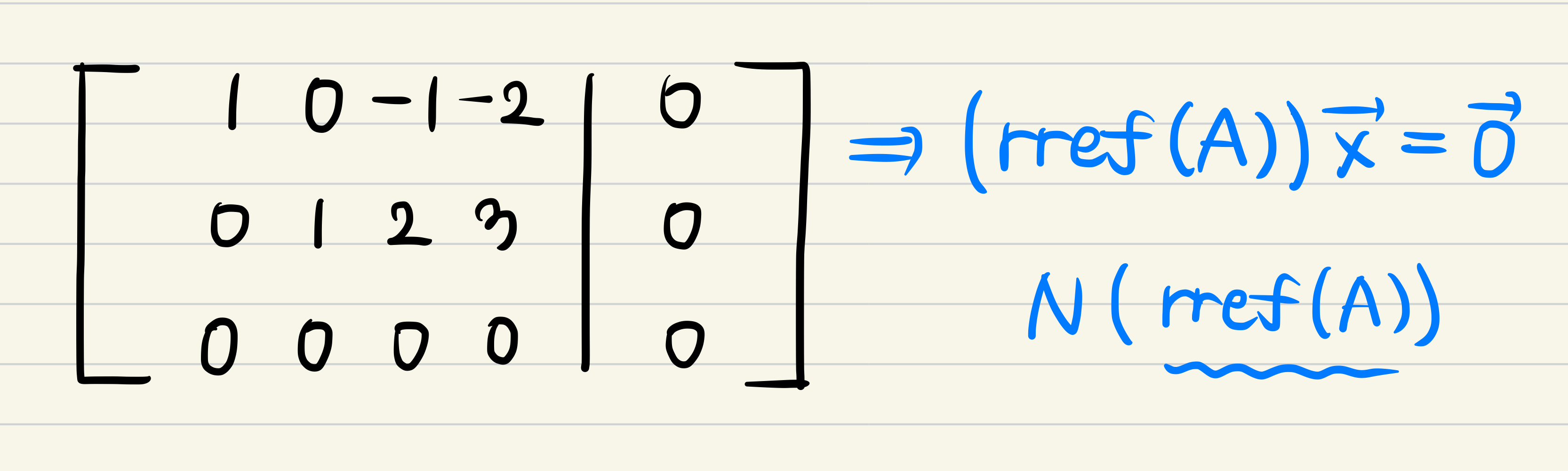Matrix vector product

• Let's define Ax, A is a matrix and x is a vector.
  • If we have A matrix shaped m by n, and x vector shaped n by 1,
    we can define b vector shaped m by 1.

• Example
  • The conclusion is Each component of Matrix vector product is as same as well the product of matrix A's each column and x vector".

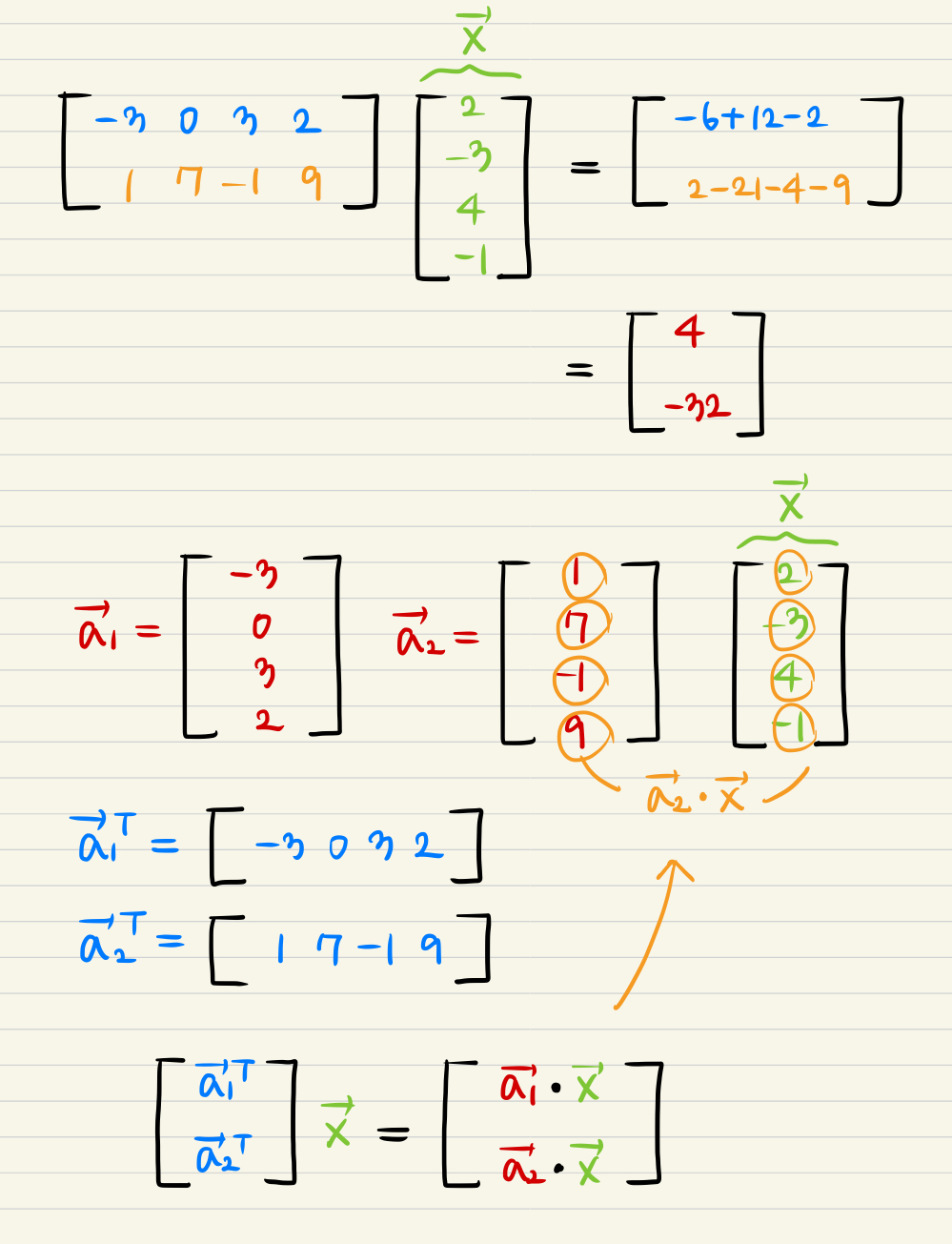
• Definition of Ax means linear combination of column vectors of A, and also
  weighted combination!
  • x vector is a weight of features extracted about A data matrix.
  • It can be used as Weight and Bias by defining Hypothesis in data science

Null space of a matrix

Part 1 : Introduction

• Remind this.
  Subspace S must be satisfied 3 conditions.
  1. 0 vector has to be in the space.
  2. If v1 and v2 vectors are in the space, v1+v2 is also, closed by addition.
  3. If constant c and v1 are in the space, c*v1 is alse, closed by multiplication.

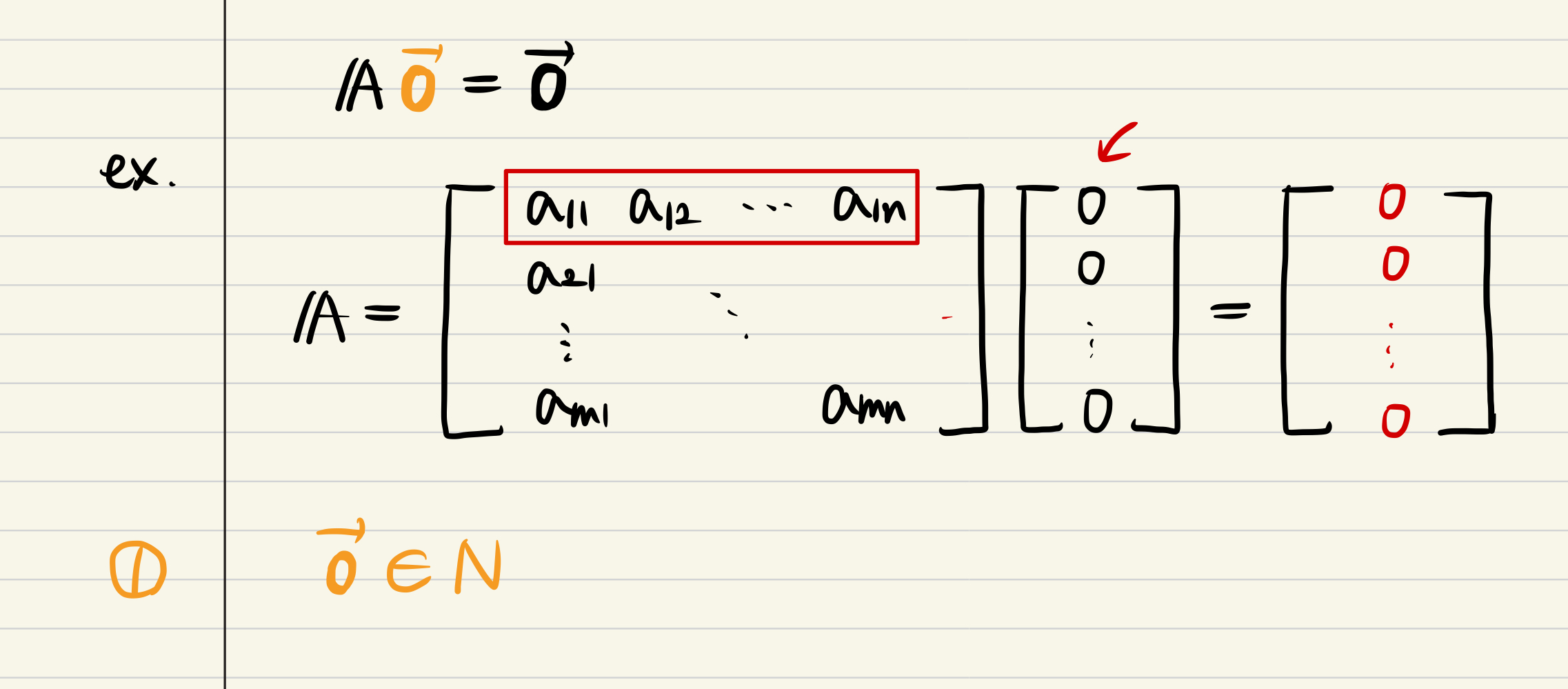
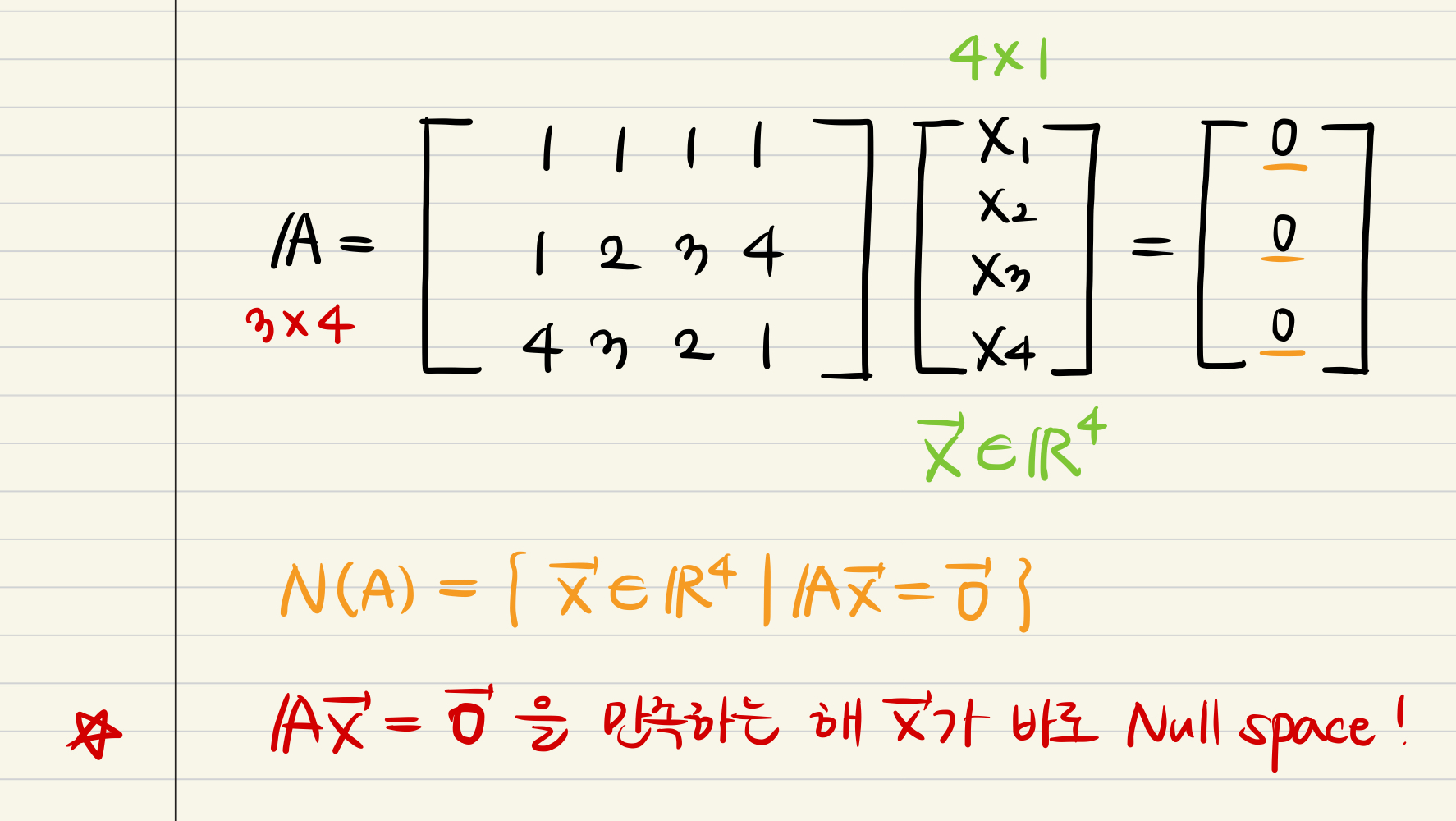
• What's the Null space?
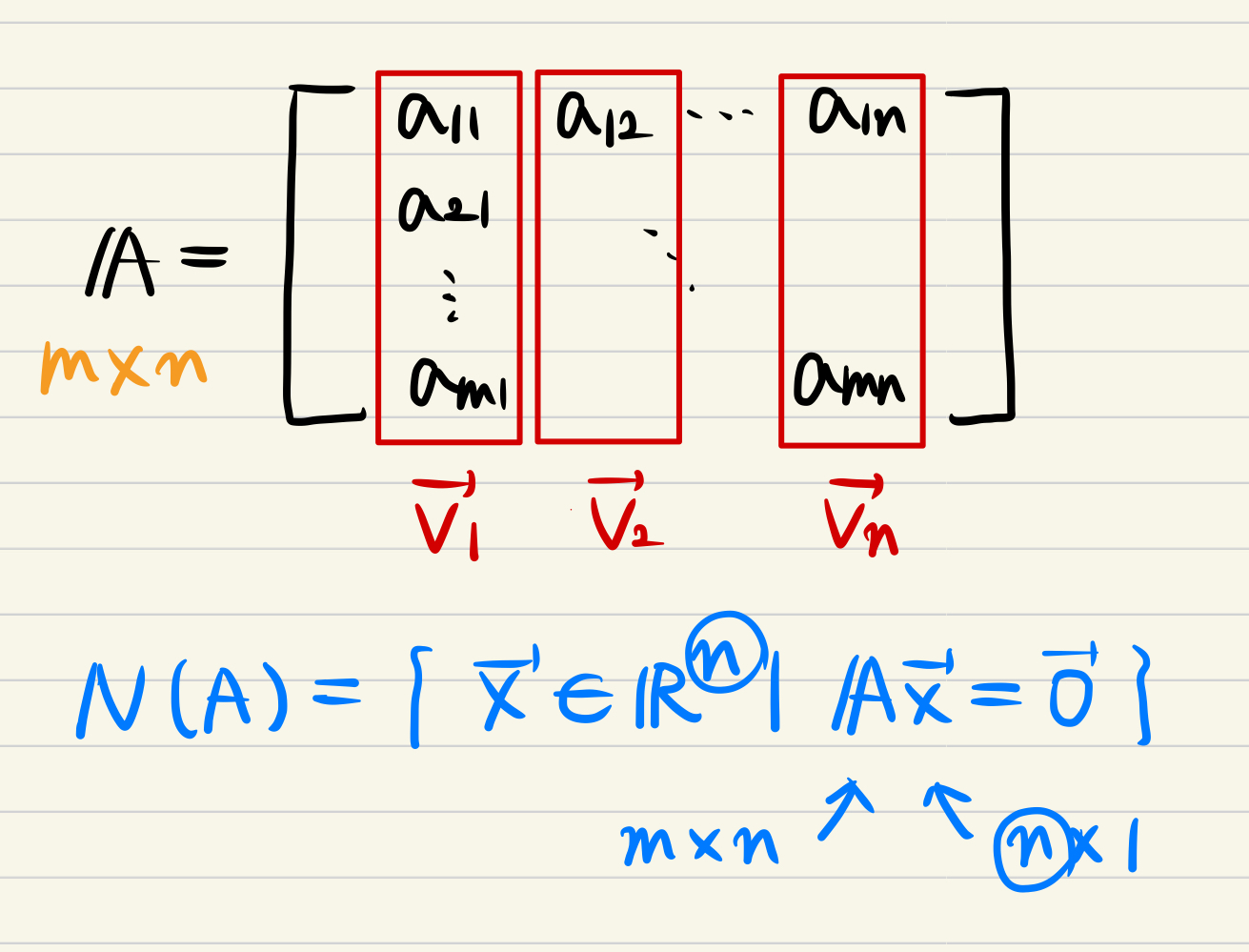
  • If we have A matrix and x vector, defining Null space(A) means that find out
    the sets of x vector which is satisfied Ax = 0 formula.
    • The right side of formula would be 0, it calls homogeneous.

• Here comes the proof that Null space satisfy above 3 conditions

Part 2 : Calculating

• Let's find out the Null space of x vector.

• First, we should define rref(A).
  • And figure out what is the pivot variable and free variable.

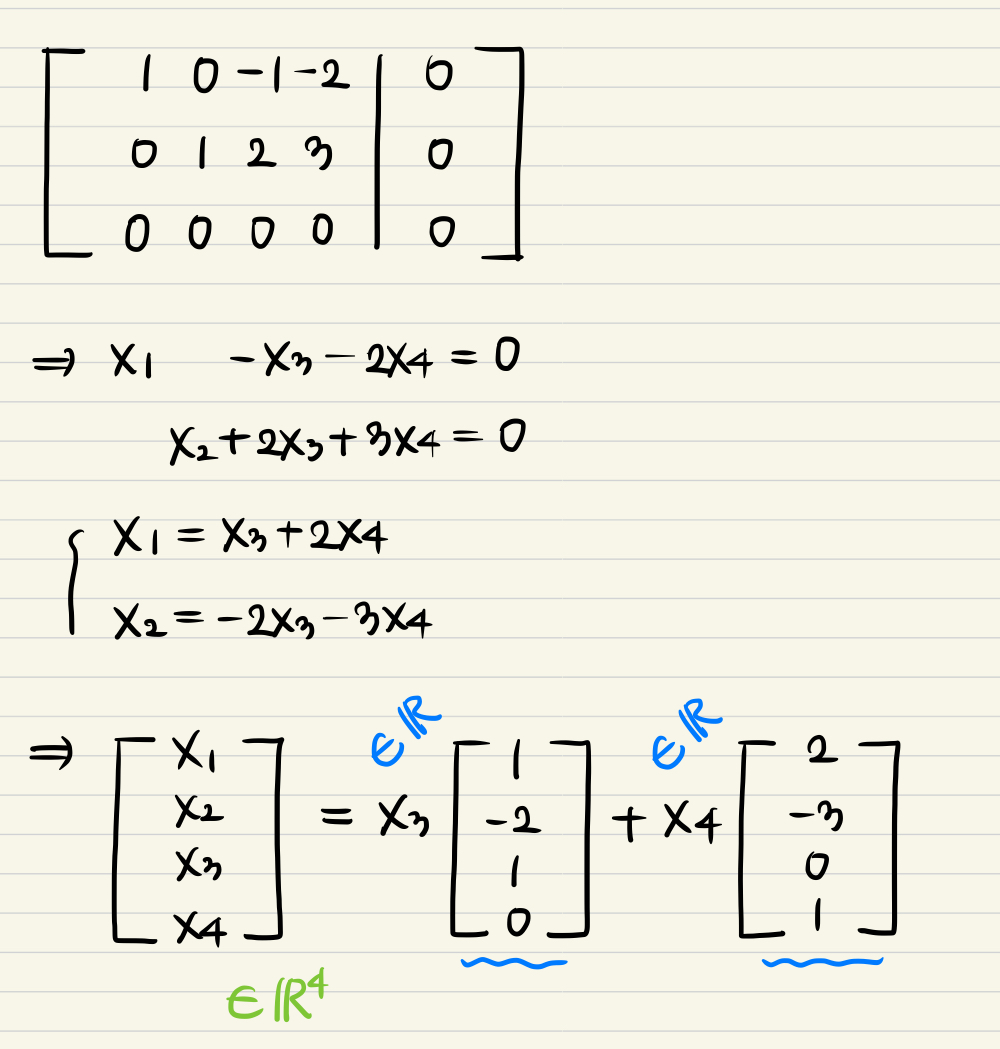
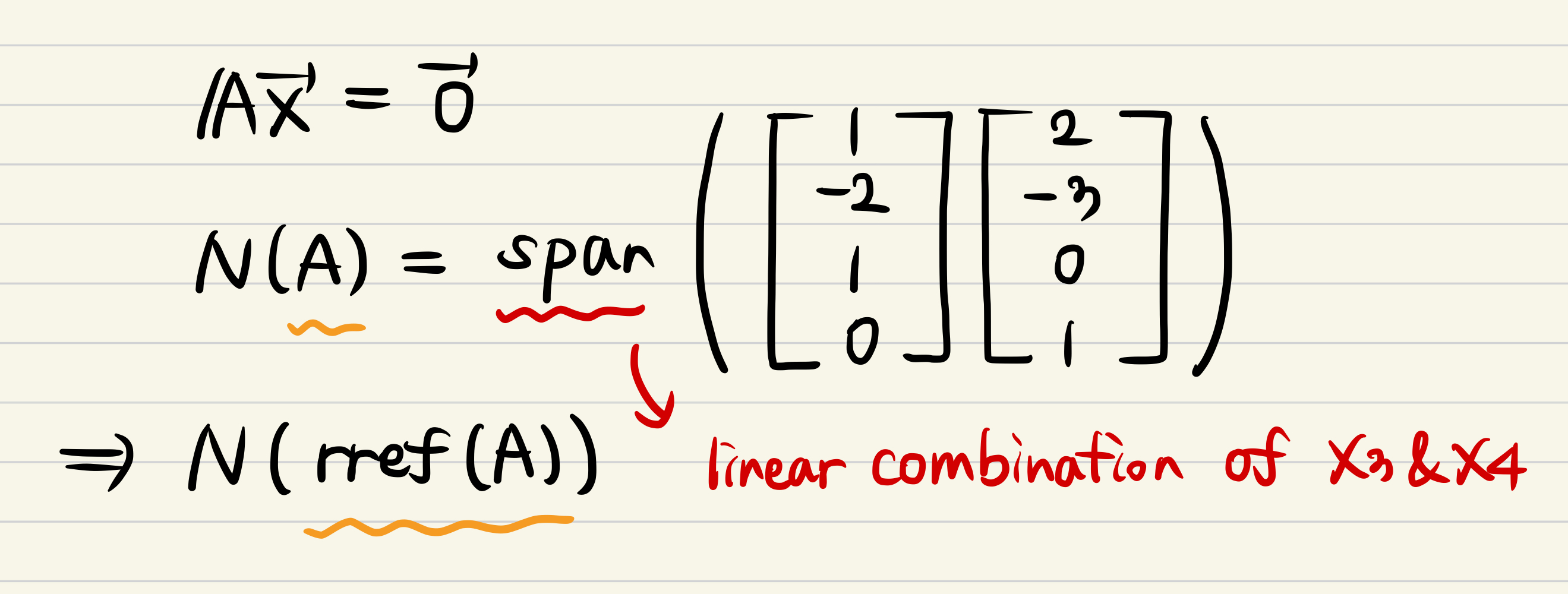
• By using what we figured out, we can represent to linear combination of pivot entries.
  • Linear combination means spanning the space!
  • And then, N(A) is equal to N(rref(A))

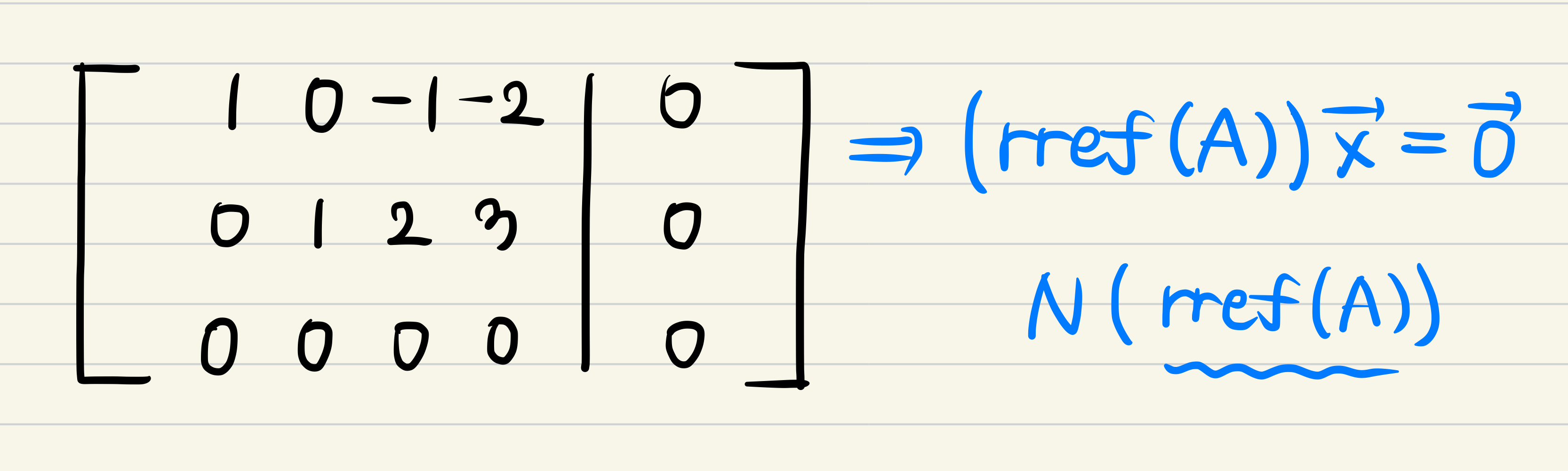
Part 3 : Linear Independent

• If we have A matrix shaped m by n, definition of Null space(A) should by like this.
  • x vector should be shaped n by 1!

• This formula would be like this.

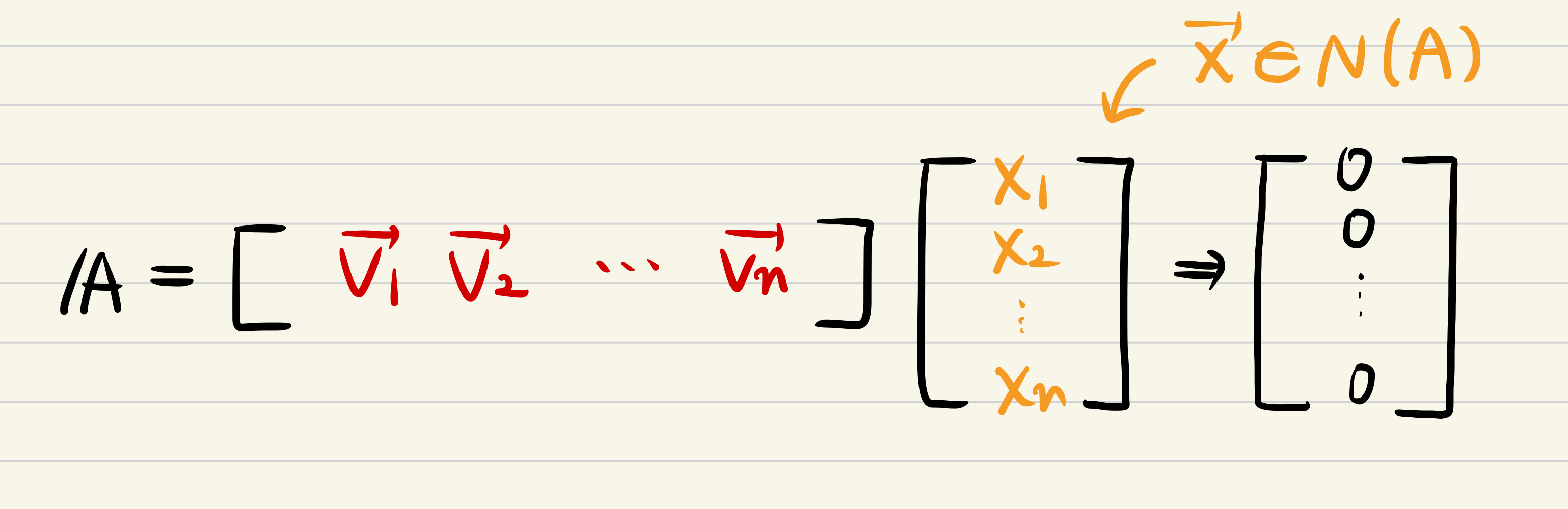
• As we got before, "Linearly Independent" means if the only solution is that all components of 0, to making the linear combination to be 0.
  • And then we could also say that Null space A has only set of 0.