벡터와 공간 | 선형결합과 생성

Linear Combination

• There are v1, v2, ... vn vectors in real Ndim space,
  when we can combine const * vec all of it (const is also in real Ndim space),
  it calls linear combination
• If some vectors are not parallel, spaning (vec a, vec b, ... ) is in Real Ndim space!
  • But some vectors are parallel, spaning (vec a, vec b, ... ) is always in same line. → It can not represent another direction

• Example : vec x is represented linear combination by vec a and vec b
• After, we call this 'linear dependent'

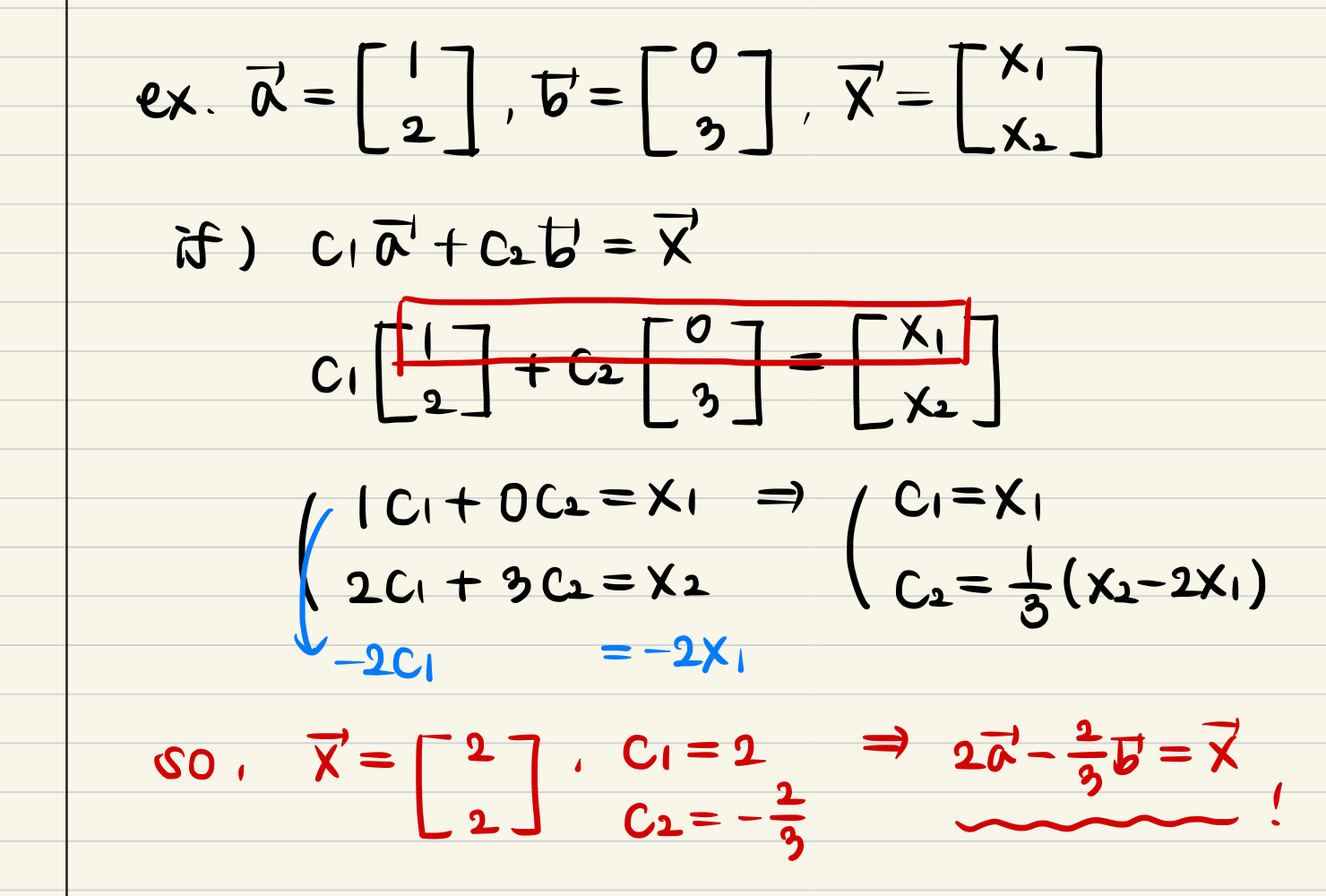
• What if the vec a and b is an orthogonal basis vector, like i and j?
• In the future, we can say that the orthogonal vectors are basis vector, and these are the minimum sets of 'spanning' in real dimensional space!