혼자 공부하는 머신러닝을 참고
선형 회귀(Linear Regression)
- 많이 사용되는 대표적인 회귀 알고리즘
- 2개의 변수 사이에 서로 상관관계가 직선으로 나타날 때 사용
- 변수를 x,y 로 놓으면 x,y의 선형 관계식은 y=θ0*x0+θ1*x1+θ2*x2+⋅⋅⋅ +θn*xn 로 나타냄
- x는 독립변수;y는 종속변수;θ0,θ1는 모델의 파라미터
- x와 파라미터들의 선형관계식을 이용해서 y의 값을 예측
- x에 대해 연속형 출력변수 y를 예측
선형 회귀 분석의 4가지 기본가정
1) 선형성
- 종속변수와 독립변수간의 선형성을 만족
2) 독립성 - 다중 회귀 분석에서 중요
- 독립변수 x들이 서로 상관관계가 없이 독립성을 만족해야 함
- 만약, 다중공선성(서로 상관관계가 있음) 이 존재한다면 제거해 주어야 함
3) 등분산성 - 분산이 서로 관계를 가지지 않고 고르게 분포
- but, 등분산성의 주체는 표준화 잔차인데 표준화 잔차가 서로 관계를 가지지 않고 고르게 분포해야 함
용어정리)
- 오차 : 모집단으로부터 추정한 회귀식으로부터 얻은 예측값과 실제 관측값의 차이
- 잔차 : 표본에서 회귀식으로 예측한 값과 실제 관측값의 차이
- 표준오차 : 표본평균의 표준편차
- 표준화 잔차 : 잔차를 잔차의 표준오차로 나누어 표준화한 것4) 정규성
- 잔차가 정규분포를 따라는 지 확인
단순 선형 회귀
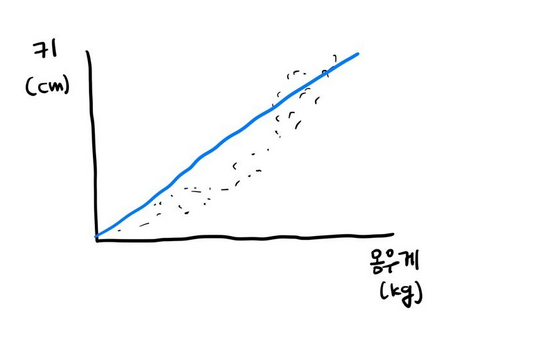
- 독립변수의 개수가 1개인 경우
예시)
x=키
y=몸무게
y=θ1*x+θ0다중 선형 회귀(Multiple Linear Regression)
- 독립변수가 2개 이상인 경우
- 독립변수들과 종속변수는 선형 관계
- 각각의 독립변수가 파라미터를 통해서 종속변수에 얼마나 영향을 미치는 지 파악 가능
예시)
x1=키
x2=식사량
y=몸무게
y=θ2*x2+θ1*x1+θ0
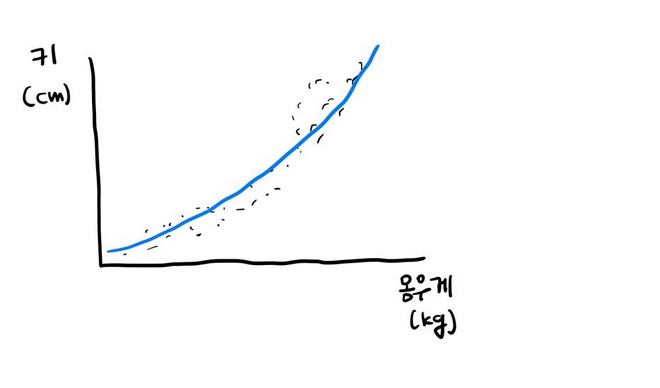
다항 회귀(Polynomial Regression)
- 독립변수와 종속변수가 선형 관계가 아닌 경우
- 비선형 회귀분석
- 위의 단순 선형회귀 예시를 보면 선형관계보다 관계를 더 잘 표현하는 방법 존재할 것으로 생각 -> 비선형 관계식으로 표현
- 문제점 존재->과적합 문제(후에 다른 게시물에 정리)
예시)
x=키
y=몸무게
y=θ2*x^2+θ1*x+θ0