[ML] Classification : Logistic Regression

Logistic Regression : 주어진 데이터(x)를 통해서 사건의 발생 확률(y)를 예측하는 통계 모델 / Linear Regression을 분류 모델로써 확장한 모델.

Definition

• Linear Regression은 특정 수치값(numeric value, continuous)을 예측하는 것에는 좋지만, 특정 카테고리(categorical value, discrete)를 예측하는데는 적합하지 않음. (직선하나로 0,1 구분짓게 어렵, 곡선으로 변경?)
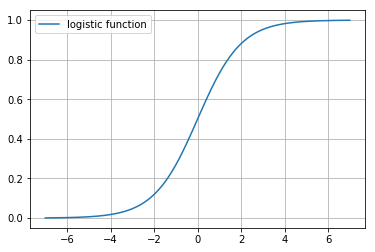
• Linear Regression 결과에 적당한 함수(activation function: sigmoid)를 적용하여 ouput score룰 0,1 사이의 값으로 변환하는 것으로 카테고리가 나올 확률을 예측하는 문제로 변환.
• 이 확률값은 예측값이 1이 될 확률이며, 이 확률이 0.5를 넘기면 1로 예측하고 그렇지 않다면 0으로 예측을 하는 분류 모델로써 사용할 수 있음.
• 이것도 loss functon: gradient descent로 학습 가능.

Go Detail

• 아래 수식은 Linear Regression의 결과를 확장한 것. → $e^{-(Wx + b)}$

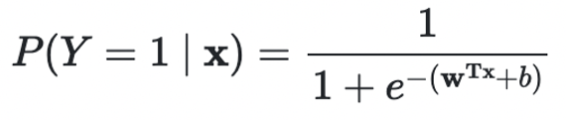
• Linear Regression의 계산 결과를 $z$라고 하면, Logistic function(또는 Sigmoid function)을 계산한 결과가 위의 수식.
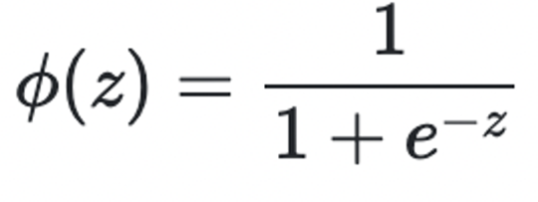
  • Logistic Function = sigmoid
    

• Logistic function은 무한대의 범위를 가지는 $z$를 [0, 1] 사이의 값으로 바꿔줌.
• 이 때 [0, 1] 사이의 값은 예측값이 1이 될 확률로 해석.
• 즉, Equation A을 봤을 때 input x가 들어가고 최종적으로 [0 ,1] 사이의 확률이 나온다고 생각하고 그 확률은 최종적으로 1이라는 target value가 나올 확률. 이 확률이 0.5(물론 나중에 evalation metrics 변환하면 바꿀 순 있음 일단은 직관적으로 0.5라 이해 ㄱ)를 넘으면 1이라고 예측값을 출력.
  • 여기서도 업데이트 되는 파라미터는 여전히 $W$와 $b$ .