ML VS DL
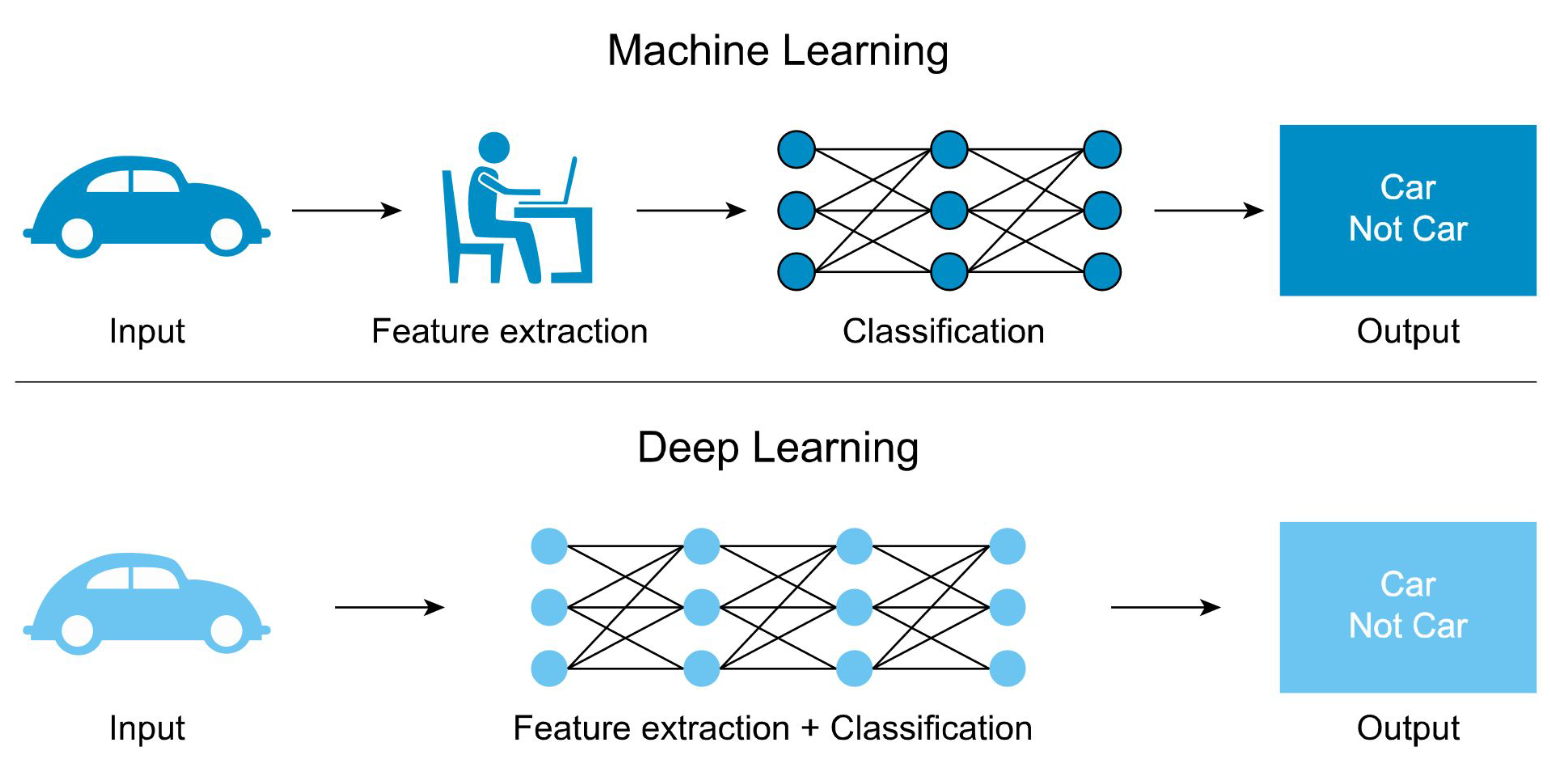
규칙 기반과 딥러닝 기반 기계학습
규칙 기반 모델
• 적은 양의 데이터로 일반화 가능
• 결론 도출의 논리적 추론 가능
• 학습에 필요한 데이터가 비교적 적게 필요
• 이를 제작한 전문가의 실력을 넘어서기 매우 어려움
• 해당 전문가의 오류를 동일하게 반복
• 규칙 구축에 많은 시간과 비용 소요
• Toy task에 주로 적용되었음
딥러닝 기반 모델
• 학습에 사용할 데이터의 질이 좋고 양이 많으면 인간의 실력을 넘어설 수 있음
• 인간이 생각하지 못한 새로운 방법을 사용할 수 있음
• 기본적으로, 많은 데이터가 필요함
• 논리적 추론이 아닌 귀납적 근사에 의한 결론 생성 • 결과에 대한 해석의 어려움
• 규칙 구축에 많은 시간과 비용 소요
딥러닝과 NLP
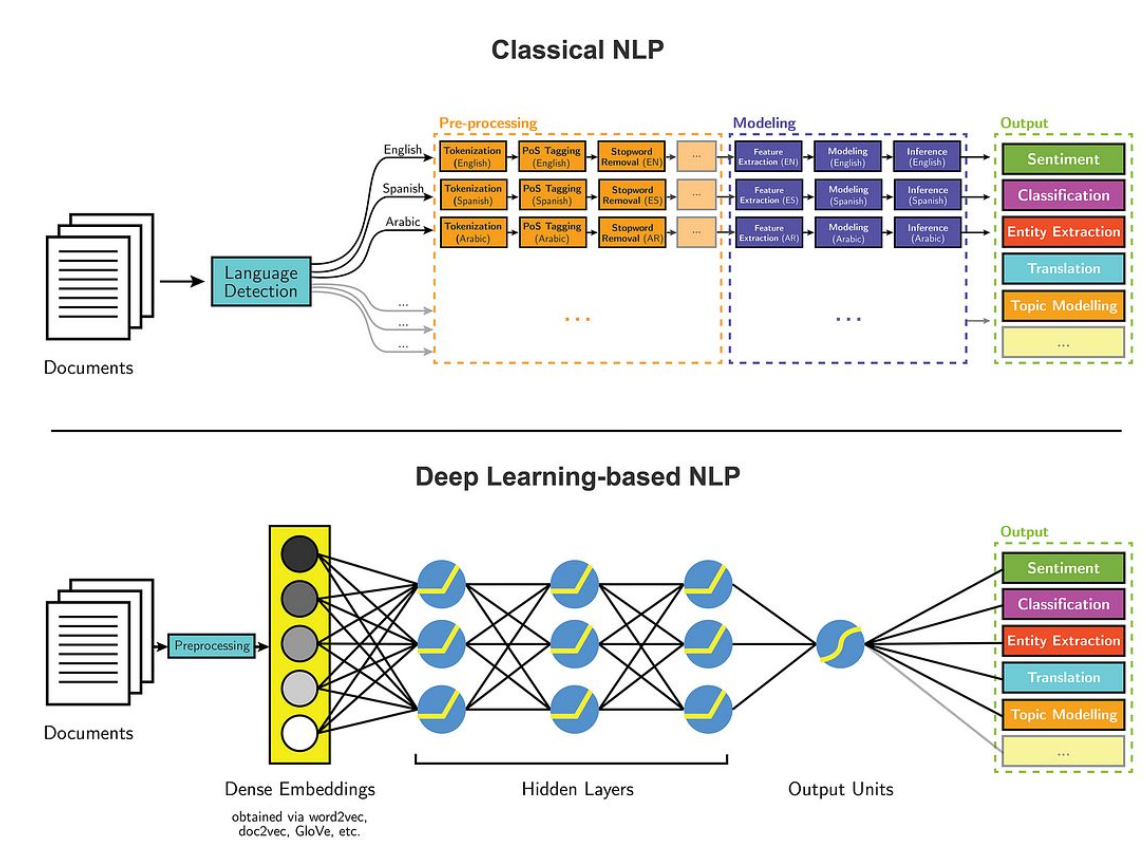
딥러닝 학습 방법
- 신경망 레이어의 출력 값은 레이어를 구성하는 가중치(파라미터)들의 값에 의해 결정
- m개의 입력을 받아 n개의 값을 출력하는 완전연결층은 m×n개의 입력 가중치 값과 n개의 편향 가중치(bias) 값이 있음
- 딥러닝 모델들에는 입력 데이터와 출력 데이터를 처리하기 위해 보통 수천개 이상의 파라미터가 사용되고, 레이어의 수도 수십에서 수백에 이름
- 이 외에도 모델의 여러 특성들을 결정하는데 가중치 값들이 사용됨 딥러닝 모델은 수천만에서 수억, 수십억 개 이상의 가중치들로 이루어져 있음
- 원하는 출력을 만들어내기 위해서는 모든 파라미터의 값을 정밀하게 조정해야 함
- 딥러닝은 파라미터에 따라 매우 다양한 입력-출력을 학습 가능함
- 예를 들어, 이미지를 입력받아 카테고리를 출력하는 이미지 분류 또는
카테고리를 입력받아 이미지를 출력하는 이미지 합성 등이 가능함
- 예를 들어, 이미지를 입력받아 카테고리를 출력하는 이미지 분류 또는
- 딥러닝에서의 학습은 수많은 파라미터들의 최적 값을 찾아가는 과정을 의미함
- 정방향 계산(forward pass)은 입력으로부터 예측을 만들어내는 과정을 의미함
- 이 과정에서는 입력 데이터가 모델을 통과하며 각 계층의 가중치와 연산을 통해 출력(예측)이 생성됨
- 역방향 계산(backward pass)은 예측과 정답 사이의 차이를 줄이는 방향으로 파라미터를 수정하는 과정을 의미함
- 손실 함수를 통해 계산된 오차가 네트워크를 역방향으로 통과하며, 각 계층의 가중치는 오차를 최소화하는 방향으로 업데이트됨
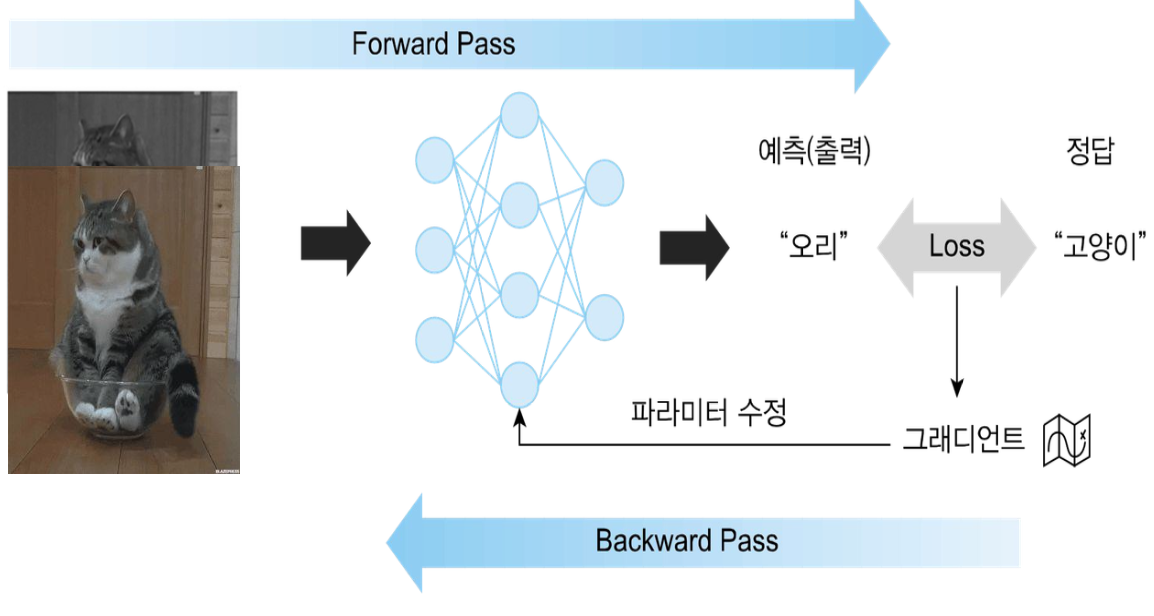
- 손실 함수를 통해 계산된 오차가 네트워크를 역방향으로 통과하며, 각 계층의 가중치는 오차를 최소화하는 방향으로 업데이트됨
• 손실 함수(loss function)는 모델의 예측과 정답 사이의 차이를 수치화시켜주는 함수
• 이를 통해 모델의 성능을 측정하고, 이를 기반으로 모델을 개선할 수 있음
• 손실 함수의 값을 각각의 파라미터들에 대해 편미분하면 그래디언트(gradient)를 계산할 수 있음
• 그래디언트는 손실 함수의 기울기를 나타내며, 이를 통해 파라미터를 어떻게 수정해야 손실을 줄일 수 있는지 알 수 있음
• 그래디언트에 따라 파라미터들을 수정하면, 현재 입력에 대한 모델의 예측이 정답에 가까워짐
• 이는 그래디언트가 손실을 줄이는 방향을 가리키기 때문임
• 이러한 과정을 모든 데이터에 대해 반복적으로 적용
• 이를 통해 모델의 모든 파라미터를 최적화하고, 전체적인 성능을 향상시킬 수 있음
• 딥러닝 모델에서 손실 함수에 대한 입력층의 그래디언트는 편미분의 특성상 한 번에 계산할 수 없음
• 각 계층의 출력이 다음 계층의 입력으로 사용되기 때문임
• 손실 함수에 대한 출력층의 그래디언트를 계산하고, 이로부터 다시 이전층의 그래디언트를 계산하는 방식으로 연쇄 법칙 (chain rule)을 이용
• 출력에서 입력으로 계산이 역방향으로 진행되기 때문에 역전파(back-propagation)라고 함
• 모델의 파라미터를 손실을 줄이는 방향으로 업데이트하는 데 사용됨
• 딥러닝 모델의 학습에는 미분값이 큰 영향을 미치며, 손실 함수로부터 편미분값을 계산할 수 있는 가중치들만 역전파 알고리즘을 이용하여 값을 학습할 수 있음
