동적 계획법
파이썬의 경우,
문제를 작게 분할한 다음, 분할한 문제의 정답을 리스트에 저장하고(Memoization) 상위로 한 단계씩 올라갈수록 구했던 정답을 꺼내 쓰는 방식의 프로그래밍.
1. 피보나치 수열
피보나치 수열을 예로 들어보자.

def fib(n: int) -> int:
if n == 0:
return 1
if n == 1:
return 1
return fib(n - 1) + fib(n - 2)
print(fib(4))동적 계획법을 사용하지 않은 피보나치 수열 함수이다. 위 그림에서 호출된 함수를 보면, 4번째 피보나치 수열 항을 구하기 위해서 fib(0)이 2번 리턴되고, fib(1)이 3번 리턴되고, fib(2)이 2번 리턴되고… 하는 식으로 중복되어 계산하는데, 이는 연산에서 비효율적인 출입이 있다고 볼 수 있다.
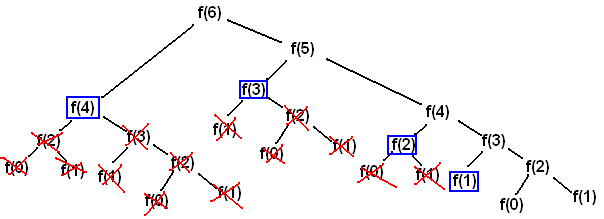
동적 계획법에서의 피보나치 수열 함수는 중복 계산이 없다. 따로 앞서 구한 값들을 저장하는 리스트에서 꺼내쓰면 되기 때문이다. 따라서 빠르게 고위 피보나치 항을 계산할 수 있다.
- CODE - fibonacci 함수 DP로 구현 (Top-Down)
이것은 동적 계획법 중 재귀를 활용한 Top-Down 방식이고 for 문을 활용하여 bottom-up 방식으로 구현할 수도 있다.# fibonacci 함수 DP로 구현 (Top-Down) def fib_DP(n: int, memo_fib: list[int]) -> int: if n < 2: return 1 if memo_fib[n] == 0: memo_fib[n] = fib_DP(n - 1, memo_fib) + fib_DP(n - 2, memo_fib) # 꺼내쓰기 return memo_fib[n] n = 100 # memo_fib: 메모이제이션을 담당하는 변수 memo_fib = [0 for _ in range(n)] fib_n100 = fib_DP(n, memo_fib) # 573147844013817084101 print(fib_n100)
동적 계획법은 메모이제이션(Memoization)을 통해 아직 한 번도 계산이 안 된 항이 있다면 fib(0), fib(1), fib(2), …을 모두 한 번씩만 계산한 뒤 리스트에 저장하고 상위 피보나치 항에서 필요할 때마다 뽑아쓰는 방식으로 사용할 수 있다.
- CODE - fibonacci 함수 DP로 구현 (Bottom-Up)
# fibonacci 함수 DP로 구현 (Bottom-Up) def fib_DP(n: int, memo_fib: list[int]) -> int: if n < 2: return 1 fir = 1 sec = 1 for i in range(2, n + 1): memo_fib[i] = fir + sec fir = sec sec = memo_fib[i] return memo_fib[n] n = 100 # memo_fib: 메모이제이션을 담당하는 변수 memo_fib = [0 for _ in range(n + 1)] fib_n100 = fib_DP(n, memo_fib) # 573147844013817084101 print(fib_n100)
2. 가장 긴 오름차순 부분 수열
다음은 어떤 무작위 수열에서 가장 긴 오름차순의 부분 수열을 구하는 문제이다.
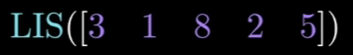

[3, 1, 8, 2, 5]의 리스트에서 가장 긴 오름차순 부분 수열은 [1, 2, 5]이며 길이는 3이다. 위 리스트의 요소들을 위상정렬에서 배운 DAG로 다시 표현하면 아래 그림과 같다.
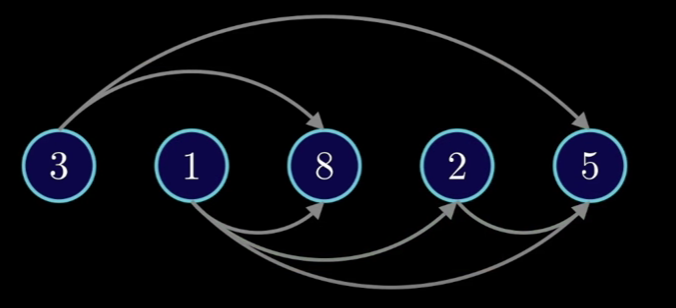
이제 오름차순으로 뽑을 수 있는 부분수열이 DAG로 시각화되어 훨씬 보기 편해졌다. 해당 리스트에서 2개 이상 길이의 오름차순으로 뽑을 수 있는 부분수열은 다음과 같다.
- [3, 8]
- [3, 5]
- [1, 8]
- [1, 2]
- [1, 5]
- [1, 2, 5]
이 중 가장 길이가 긴 부분수열은 [1, 2, 5]로 위 문제에서 원하는 답은 이 수열의 길이 3이다. 여기서 보통은 백트래킹으로 for문 안에 재귀함수를 넣어서 모든 부분수열을 고려하는 방식을 생각할 것이다.
- 전형적인 모든 부분수열을 찾는 백트래킹 코드를 잘 생각해보자.
출력값:nlist = [3, 1, 8, 2, 5] def bacaktracking(nlist: list[int], idx: int, printlist: list[int] = []): printlist.append(nlist[idx]) print(printlist) for i in range(idx + 1, len(nlist)): bacaktracking(nlist, i, printlist) printlist.pop() bacaktracking(nlist, 0)-
[3]
-
[3, 1]
-
[3, 1, 8]
-
[3, 1, 8, 2]
-
[3, 1, 8, 2, 5]
-
…
위 코드에서 프린트되는 모든 부분수열을 보면 중복되는 요소들이 많다. 여기서 DP를 활용한다면 이 중복되는 요소를 모두 한번 뽑아다 쓰는 것으로 대체해버릴 수 있다. 여기서 구한 경우의 수를 저장하는 리스트 L가 필요한데, DFS나 BFS 코드의 visited 변수를 생각하면 편하다.
예를 들면 이런 식이다.
-
[3] → 출력값 L[0]에 저장
-
[L[0] 1] → 출력값 L[1]에 저장
-
[L[1] 8] → 출력값 L[2]에 저장
-
[L[2] 2] → 출력값 L[3]에 저장
-
[L[3] 5] → 출력값 L[4]에 저장
-
…
이렇게 하면 이미 앞에서 구한 같은 순서의 요소들에 대한 출력값을 리스트 L에서 한번 뽑아오는 것으로 여러번의 재귀를 스킵할 수 있다.
-
우리는 백트래킹의 구조를 따르지 않고, N길이의 2중 for문으로 nlist의 인덱스 방향으로 진행도를 체크하면서 현재까지의 진행도에서 가장 긴 오름차순 수열의 길이를 갱신해나갈 것이다. 그럼 갱신한 길이를 저장할 리스트 L이 따로 필요할 것이고, 다음 인덱스에서 가장 긴 오름차순 수열을 갱신할 때 앞에서 저장한 최대 길이를 그대로 가져와 더할 것이다.
- CODE - 가장 긴 오름차순 부분 수열 (Bottom-Up)
nlist = [3, 1, 8, 2, 5] def longestSortedSubset(nlist: list[int], n: int) -> None: # L: 메모이제이션을 담당하는 변수 ## 모든 공집합이 아닌 부분집합은 for문이 처음 돌 때 길이가 1이므로 모든 값이 1로 초기화된 N 길이의 리스트를 하나 만든다. L = [1] * n # 인덱스의 진행도를 나타내는 for 문 ## range(1, n): 0번째 진행도에서의 최대 길이는 1일게 뻔하므로 스킵 for i in range(1, n): # subLongest: 앞 L 요소 중 최대값을 뽑아내기 위해 임시로 담을 리스트 변수 subLongest = [] # 현재 진행중인 인덱스의 앞 요소들을 조회하기 위한 for 문 for k in range(i): # 오름차순 조건 if nlist[k] < nlist[i]: subLongest.append(L[k]) # 현재 진행도에서 가장 긴 오름차순 수열 갱신 L[i] = 1 + max(subLongest) return max(L) print(longestSortedSubset(nlist, len(nlist)))
DP의 장단점
장점
- 최적의 바텀-업 구조: 동적 프로그래밍은 큰 문제에 대한 솔루션이 하위 문제에 대한 솔루션으로 구성될 수 있는 최적의 바텀-업 구조로 문제를 해결하는 데 효과적이다.
- 시간 복잡성: 동적 프로그래밍은 특정 문제에 대한 재귀 솔루션에 비해 시간 복잡성을 크게 줄일 수 있다.
단점
- 공간 복잡성: 특히 하위 문제가 많은 문제를 해결할 때 중간 결과를 저장하는 데 더 많은 메모리가 필요할 수 있다.
- 구현의 복잡성: 동적 프로그래밍 알고리즘은 설계하고 이해하기가 복잡할 수 있으므로 하위 문제 및 전환을 신중하게 식별해야 한다.
- 모든 문제에 적합하지 않음: 동적 프로그래밍을 사용하여 모든 문제를 효율적으로 해결할 수 있는 것은 아니며 경우에 따라 최적의 바텀-업 구조와 겹치는 또다른 하위 문제를 식별하는 것이 어려울 수 있다. 전반적으로 동적 프로그래밍은 최적화 문제를 효율적으로 해결하는 데 유용한 도구이지만 특정 문제에 적용할지 여부를 신중하게 고려해야 한다.
