연결 요소(Connected Component)
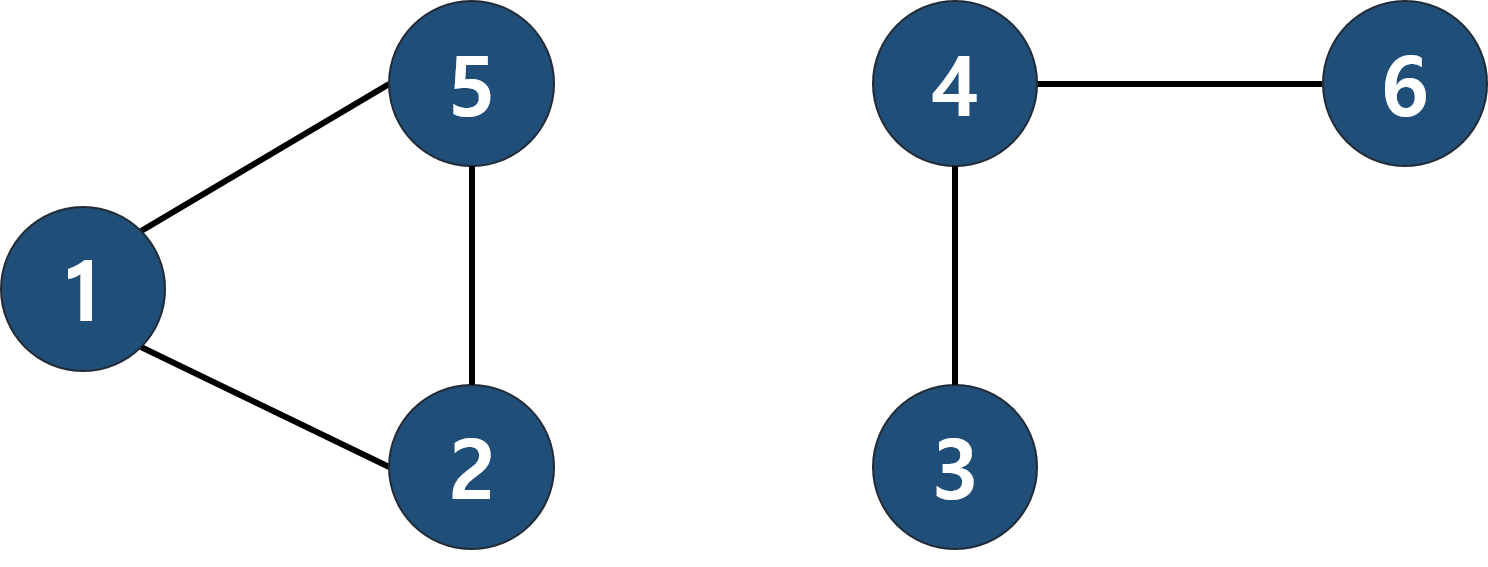
그래프 중에서는 위 그림과 같이 여러 개로 나누어져 있을 수도 있다. 위 그림을 보고 두 개의 그래프라고 볼 수도 있지만, 하나의 그래프에 두 개의 연결 요소를 가진다고 볼 수도 있다. 그 이유는 정점 사이에 겹치는 것이 없기 때문이다. 연결 요소로 본다면, 나누어진 각각의 그래프를 연결 요소라고 한다. 이때 연결 요소가 될 조건은 다음과 같다.
- 연결 요소에 속한 모든 정점을 연결하는 경로가 있어야 한다.
- 또 다른 연결 요소에 속한 정점과 연결하는 경로가 있으면 안된다.
그러므로, 위 그림은 2개의 연결 요소로 이루어져 있다고 볼 수 있다. 연결 요소를 구하는 것은 DFS나 BFS 탐색을 이용해서 할 수 있다.
연결 요소 관련 문제
BOJ 11724. 연결 요소의 개수
방향 없는 그래프가 주어졌을 때, 연결 요소 (Connected Component)의 개수를 구하는 프로그램을 작성하시오.
#include <cstdio>
#include <vector>
using namespace std;
vector<int> a[1001];
bool check[1001];
void dfs(int node) {
check[node] = true;
for (int i=0; i<a[node].size(); i++) {
int next = a[node][i];
if (check[next] == false) {
dfs(next);
}
}
}
int main() {
int n, m;
scanf("%d %d",&n,&m);
for (int i=0; i<m; i++) {
int u,v;
scanf("%d %d",&u,&v);
a[u].push_back(v);
a[v].push_back(u);
}
int components = 0;
for (int i=1; i<=n; i++) { // 모든 인접 리스트를 순회하면서
if (check[i] == false) { // 방문하지 않은 노드가 있다면
dfs(i); // 하나의 연결 요소 모두 방문
components += 1; // 연결 요소의 수 증가
}
}
printf("%d\n",components);
return 0;
}
