브루트 포스(무식하게 풀기)

브루트 포스는 모든 경우의 수를 다 해보는 것이다. 실제로 사람이 모든 케이스를 일일이 계산해보는 것은 바람직한 방법은 아니다. 그리고 그렇게 하다보면 실수를 하기 마련이다. 마치 고등학교 때 수능시험에서의 노가다 와 같다. 하지만 전산학에서는 엄연히 하나의 알고리즘으로서 인정받는 방법이다. 왜냐하면 컴퓨터의 엄청나게 빠른 연산이 그 부분을 해결해주기 때문이다. 따라서 우리는 어떻게(무슨 부분을) 반복할 것인지만 설계하면 된다.

프로그래밍 대회에서 대부분의 사람들이 가장 많이 하는 실수는 쉬운 문제를 어렵게 푸는 것 입니다. - 알고리즘 문제해결전략(구종만)

간단한 예로, 비밀번호가 4자리이고, 숫자로만 이루어져 있다고 한다면 0000부터 9999까지 다 입력해보면 그 중 하나는 답이 될 것이다. 경우의수는 10,000가지가 된다. (보안에서는 이를 브루트 포스 어택이라고도 한다.) 만일 사람이 직접 비밀번호를 입력하는데 1초가 걸린다면 총 10,000초로 2.7시간동안 이러한 작업을 해보아야 할 것 이다. 하지만 컴퓨터의 빠른연산으로 이러한 작업이 1초도 걸리지 않는다. 이와 같이 문제 해결에서는 특히 브루트 포스를 사용하려면 대략적인 시간복잡도를 계산해보는 것이 중요하다. 자칫하면 시간초과가 날 수 있기 때문이다.

1. 브루트 포스 설계

브루트 포스로 문제를 풀기위해서는 크게 3가지 단계를 생각해볼 수 있다.

1) 문제의 가능한 경우의 수를 계산해본다.
2) 가능한 모든 방법을 다 만들어본다.
3) 각각의 방법을 이용해 답을 구해본다.

1) 문제의 가능한 경우의 수를 계산해본다.

문제의 가능한 경우의 수를 계산해보는 것은 시간 복잡도를 대략적으로 추정하는 것이다. 이는 대부분 손으로 계산해볼 수 있으므로, 직접 계산을 통해서 구한다.

2) 가능한 모든 방법을 다 만들어본다.

이때는 단 한 가지 경우라도 빠짐없이 만들어야 한다는 점이 중요하다. 이 방법을 만들어 보는 구현 방법은 여러가지가 있다.

• 그냥 다 해보는 코드를 일일이 작성하는 방법
• for 나 while 등 반복문을 사용하는 방법
• 순열을 사용하는 방법
• 재귀 호출을 사용하는 방법
• 비트마스크를 사용하는 방법

3) 각각의 방법을 이용해 답을 구해본다.

보통 브루트 포스로 설계가 가능한 문제 내에서 이 단계는 어렵지 않다. 문제에 나와있는 대로 답을 계산해보면 답이 나오는 경우가 많다.

2. 경우의 수

브루트 포스 문제의 시간복잡도는 대부분 O(경우의 수 * 방법1개를 시도해보는데 걸리는 시간복잡도) 이다. 그래서 문제의 가능한 경우의 수를 계산하는 것은 전체 시간복잡도를 추정하는데에 있어서 중요하다. 다음과 같은 경우에 각 경우의 수는 어떻게 될까?

• N명의 사람이 한 줄로 서는 경우의 수
• N명의 사람 중에서 대표 두 명을 뽑는 경우의 수
• N명의 사람 중에서 대표 세 명을 뽑는 경우의 수
• N명의 사람 중에서 반장 1명과 부반장 1명을 뽑는 경우의 수
• N명의 사람이 있을 때, 각 사람이 영화를 볼지, 보지 않을지 결정한다. 가능한 조합의 수

우선, 첫번째 경우는 한명 씩 줄을 서는 경우이므로 N명 중에 한명, N-1명중에 한명, N-2명중에 한명, ... , 마지막 1명 까지 총 N!가지 경우가 된다. 두번째는 N Combination 2 와 같으므로 N(N-1)/2 이다. 세번째는 두번째와 마찬가지로 N Combination 3 이므로 N(N-1)(N-2)/3! 이다. 네번째는 반장과 부반장을 각각 뽑는 경우이므로 N Permutation 2 이다. 마지막은 한 사람이 영화를 보거나(o), 보지않거나(x) 두 가지 경우가 있는데, N명이 있다면 2x2x2x....2 가 되어서 총 2^N 가지이다. 하... 이놈의 순열과조합..

• N명의 사람이 한 줄로 서는 경우의 수 → N × (N-1) × … × 1 = N!
• N명의 사람 중에서 대표 두 명을 뽑는 경우의 수 → N × (N-1) / 2
• N명의 사람 중에서 대표 세 명을 뽑는 경우의 수 → N × (N-1) × (N-2) / 3!
• N명의 사람 중에서 반장 1명과 부반장 1명을 뽑는 경우의 수 → N × (N-1)
• N명의 사람이 있을 때, 각 사람이 영화를 볼지, 보지 않을지 결정한다. 가능한 조합의 수 → 2^N

---

3. 브루트 포스를 활용한 문제해결

BOJ 2309. 일곱 난쟁이

• 문제링크 : https://www.acmicpc.net/problem/2309

왕비를 피해 일곱 난쟁이들과 함께 평화롭게 생활하고 있던 백설공주에게 위기가 찾아왔다. 일과를 마치고 돌아온 난쟁이가 일곱 명이 아닌 아홉 명이었던 것이다.

아홉 명의 난쟁이는 모두 자신이 "백설 공주와 일곱 난쟁이"의 주인공이라고 주장했다. 뛰어난 수학적 직관력을 가지고 있던 백설공주는, 다행스럽게도 일곱 난쟁이의 키의 합이 100이 됨을 기억해 냈다.

아홉 난쟁이의 키가 주어졌을 때, 백설공주를 도와 일곱 난쟁이를 찾는 프로그램을 작성하시오.

이 문제는 가장 기본적인 형태의 브루트 포스 문제이다. 일곱 난쟁이의 키의 합이 100이므로, 아홉명 중에 일곱 난쟁이의 키의 합이 100이 되는 순간 종료하고 일곱 난쟁이를 출력하면 된다. 하지만 그렇게 생각하다 보면 매우 복잡해진다. for문으로 구현하는 경우에는 for문이 7개가 중첩이 되어야 할 것이다. 여기서 조금만 생각을 달리하면 간단히 해결 가능하다.

아홉명의 난쟁이 중 일곱 난쟁이의 키의 합이 100이라면, 100에서 나머지 두명의 키를 뺀 값이 일곱 난쟁이의 키를 모두 합한 값이 될 것이다. 즉, 아홉 명 중에 일곱 명을 고르는 것은 아홉명 중에 두명을 고르는 것과 같다. 수학적으로는 9 Combination 7 는 9 Combination 2 과 같으므로 2명을 기준으로 브루트 포스를 실행하면 된다.

이때 시간 복잡도는 O(난쟁이 두명을 고르는 경우의 수 x 일곱 난쟁이의 키의 합을 고르는 시간 복잡도) 이다. 난쟁이 수를 N이라고 했을 때, 두명을 고르는 경우의 수가 N^2의 복잡도이고 나머지 난쟁이의 키의 합을 고르는 시간 복잡도가 O(N)이므로 총 시간 복잡도는 O(N^3)이다.

#include <iostream>
#include <algorithm>
using namespace std;
int d[9]; // 난쟁이의 키를 담는 배열 
int n = 9; // 난쟁이의 수 
int main() {
    int sum = 0;
    for (int i=0; i<n; i++) {
        cin >> d[i];
        sum += d[i]; // 난쟁이의 키를 모두 합한다. 
    }
    sort(d,d+n); // 키의 오름차순으로 정렬
    for (int i=0; i<n; i++) { 
        for (int j=i+1; j<n; j++) {
            if (sum - d[i] - d[j] == 100) { // 난쟁이 두명의 키를 뺀 값이 100이면 
                for (int k=0; k<n; k++) { 
                    if (i == k || j == k) continue; // 그 두명을 제외하고 
                    cout << d[k] << '\n'; // 모두 출력 
                }
                return 0;
            }
        }
    }
    return 0;
}

구현에서는 먼저 난쟁이이의 키를 모두 합한 다음, 키의 오름차순으로 정렬 해놓는다. 그리고 i와j의 중첩반복문에서 i와 j번 난쟁이 두 명의 키를 뺀 값이 100이 되는 순간, 그 두명을 제외한 나머지 일곱 난쟁이의 키를 모두 출력하고 종료한다.

BOJ 3085. 사탕 게임

• 문제링크 : https://www.acmicpc.net/problem/3085

상근이는 어렸을 적에 "봄보니 (Bomboni)" 게임을 즐겨했다.

가장 처음에 N×N크기에 사탕을 채워 놓는다. 사탕의 색은 모두 같지 않을 수도 있다. 상근이는 사탕의 색이 다른 인접한 두 칸을 고른다. 그 다음 고른 칸에 들어있는 사탕을 서로 교환한다. 이제, 모두 같은 색으로 이루어져 있는 가장 긴 연속 부분(행 또는 열)을 고른 다음 그 사탕을 모두 먹는다.

사탕이 채워진 상태가 주어졌을 때, 상근이가 먹을 수 있는 사탕의 최대 개수를 구하는 프로그램을 작성하시오.

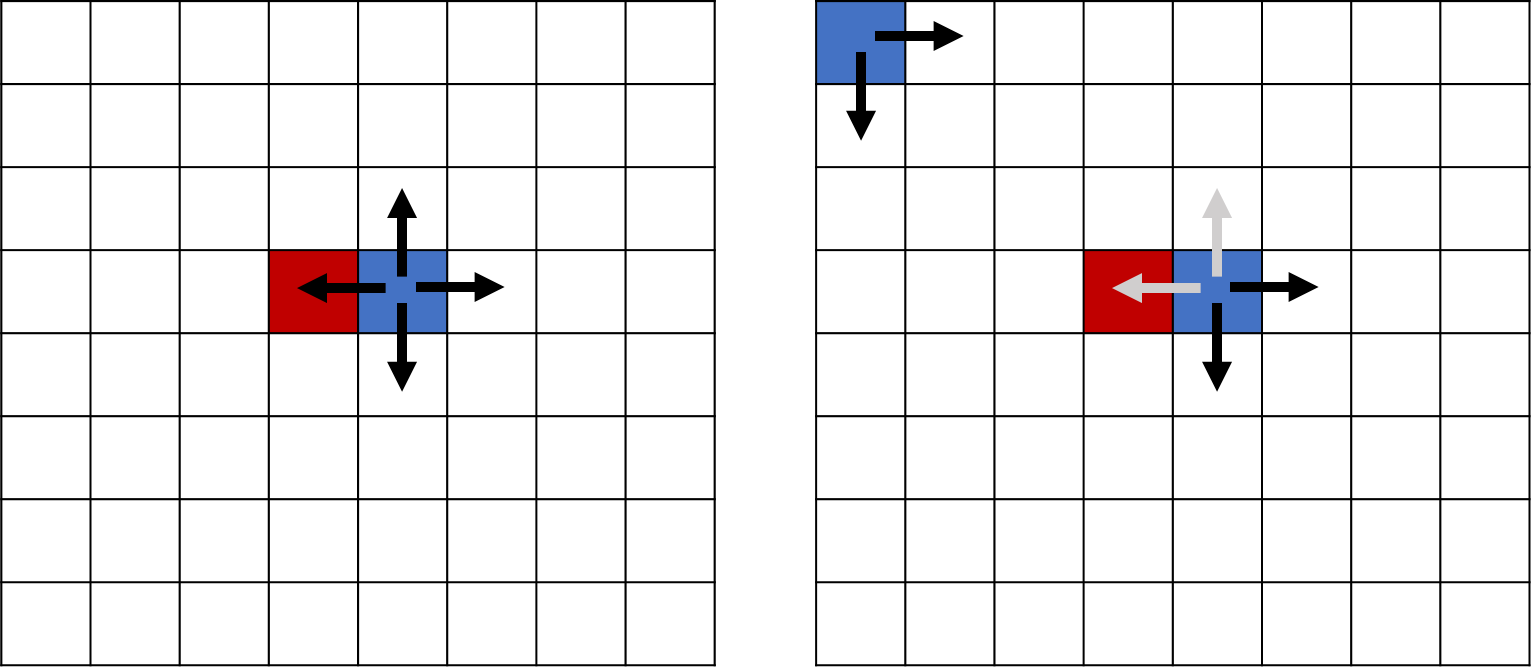
문제에서 인접한 두 칸을 고른다고 했으므로, 우선 인접한 칸을 선택하는 경우의 수는 상하좌우로 4가지이다. 그러면 NxN칸을 모두 이동하면서 교환하므로 시간 복잡도는 O(4N^2)가 된다. 그런데 여기서 (0,0)번 배열부터 시작한다면 오른쪽과 아래쪽만 교환하면 왼쪽과 위쪽은 이미 교환한 상태일 것이므로 2번만 연산하면 된다. 따라서 O(2N^2)으로 구현 가능하다.

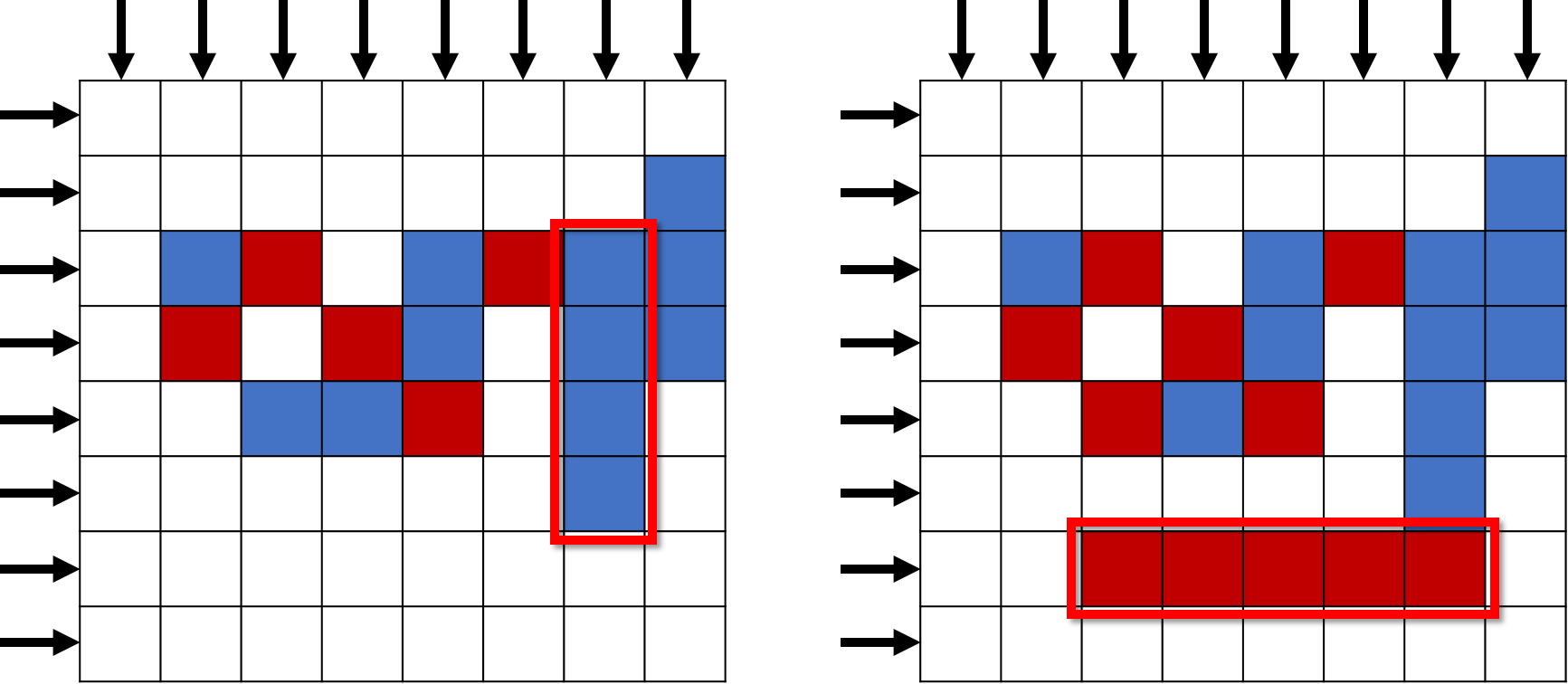
그 다음, 같은 색으로 이루어진 가장 긴 연속 부분을 구하는 것은 행과 열을 모두 확인하므로, NxN의 복잡도를 가진다. 따라서 이 부분의 시간 복잡도는 O(N^2)이다. 따라서 각 인접한 칸을 모두 교환해 보면서 최대 연속길이를 구하기 위해서는 O(N^4)의 시간 복잡도를 가지게 된다.

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int check(vector<string> &a) { // 가장 긴 연속 부분 행or열을 찾는 함수 
    int n = a.size();
    int ans = 1;
    for (int i=0; i<n; i++) { // 전체를 탐색 
        int cnt = 1;
        for (int j=1; j<n; j++) { // 각 행에서 가장 긴 연속 부분을 찾음 
            if (a[i][j] == a[i][j-1]) {
                cnt += 1;
            } else {
                cnt = 1;
            }
            if (ans < cnt) ans = cnt;
        }
        cnt = 1;
        for (int j=1; j<n; j++) { // 각 열에서 가장 긴 연속 부분을 찾음 
            if (a[j][i] == a[j-1][i]) {
                cnt += 1;
            } else {
                cnt = 1;
            }
            if (ans < cnt) ans = cnt;
        }
    }
    return ans;
}
int main() {
    int n;
    cin >> n;
    vector<string> a(n);
    for (int i=0; i<n; i++) {
        cin >> a[i];
    }
    int ans = 0;
    for (int i=0; i<n; i++) {
        for (int j=0; j<n; j++) {
            if (j+1 < n) {
                swap(a[i][j], a[i][j+1]); // 가로에 인접한 사탕을 교환했다가 
                int temp = check(a); // 가장 긴 인접 길이를 찾고 
                if (ans < temp) ans = temp;
                swap(a[i][j], a[i][j+1]); // 다시 돌려놓음 
            }
            if (i+1 < n) {
                swap(a[i][j], a[i+1][j]); // 세로에 인접한 사탕을 교환했다가 
                int temp = check(a); // 가장 긴 인접 길이를 찾고 
                if (ans < temp) ans = temp;
                swap(a[i][j], a[i+1][j]); // 다시 돌려놓음 
            }
        }
    }
    cout << ans << '\n';
    return 0;
}