
스택(Stack) 자료구조
스택은 흔히 프링글스에 비유가 된다. 프링글스 통 안에 감자칩이 쌓여있지만 우리는 가장 위에 있는 감자칩부터 꺼내는 수 밖에 없다. 즉, 마지막으로 넣은 것이 (맨위에 있으므로) 가장 먼저 나오는 Last In First Out(LIFO) 구조이다.
스택은 한쪽 끝에서만 자료를 넣고 뺄 수 있는 자료구조이다.
스택으로 할 수 있는 가장 기본적인 연산은 스택 맨 위에 값을 넣고(PUSH), 스택 맨 위의 값을 꺼내고(POP), 스택 맨위의 값을 확인하는(PEEK) 것이다. 스택 자료구조를 구현하기 위한 보편적인 ADT는 다음과 같다.
void StackInit(Stack * pstack);- 스택의 초기화를 진행한다.
- 스택 생성 후 가장 먼저 호출되어야 하는 함수이다.
bool IsEmpty(Stack * pstack);- 스택이 빈 경우 true를, 그렇지 않은 경우 false를 반환한다.
void Push(Stack * pstack, Data data);- 스택에 데이터를 저장한다. 매개변수 data로 전달된 값을 저장한다.
Data Pop(Stack * pstack);- 마지막에 저장된 요소를 삭제한다.
- 삭제된 데이터는 반환이 된다.
- Pop 함수의 호출을 위해서는 데이터가 하나 이상 존재 해야한다. ( IsEmpty() != true )
Data Peek(Stack *pstack);- 마지막에 저장된 요소를 반환하되 삭제하지 않는다.
- Peek함수의 호출을 위해서는 데이터가 하나 이상 존재 해야한다. ( IsEmpty() != true )
1. 스택의 구현
스택은 배열 기반으로 구현할 수도 있고 연결 리스트 기반으로 구현할 수 있다. 연결 리스트 기반에 비해 배열 기반으로 구현하는 것이 훨씬 간단하다.
배열 기반의 스택 구현
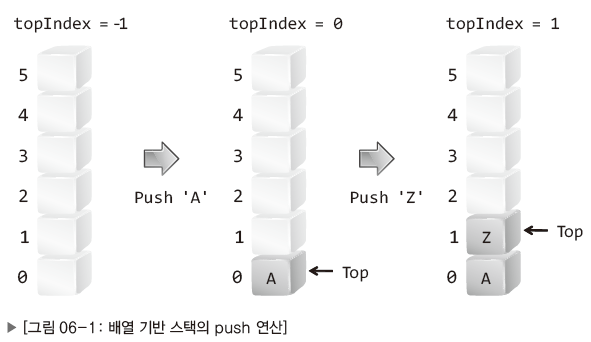
스택에서 값의 위치는 top의 위치가 결정한다. 위 그림처럼 최초의 top위치는 -1이다. 즉, -1이면 스택이 비어있다는 뜻이다. 그리고 Push('A')를 하면 A값이 스택에 저장되고 top값을 1이 증가하여 0이 된다. 한번 더 Push('Z')를 하면 top은 1이 된다. 여기에서 Pop()을 하면 top의 위치에 있던(스택의 맨 위에 있던) Z가 반환된다. 이러한 원리로 일차원 배열만으로 앞서 정의한 ADT를 그대로 구현할 수 있다.
- top은 항상 맨 위를 가리킨다.
- top은 스택의 크기와 같다.
void StackInit(Stack * pstack);- top을 -1로 초기화한다.
bool IsEmpty(Stack * pstack);- 스택이 빈 경우( top == -1 ) true를, 그렇지 않은 경우 false를 반환한다.
void Push(Stack * pstack, Data data);- top을 1만큼 증가시키고, 스택의 해당 top 인덱스에 데이터를 저장한다.
Data Pop(Stack * pstack);- IsEmpty()결과가 true이면
- 마지막에(현재 top의 위치에) 저장된 요소를 반환한다.
- top을 1만큼 감소시킨다.
Data Peek(Stack *pstack);- IsEmpty()결과가 true이면
- 마지막에(현재 top의 위치에) 저장된 요소를 반환하되 top값을 그대로 둔다.
#include <iostream>
using namespace std;
int top; // 스택의 top 인덱스
void StackInit() {
top = -1;
}
bool IsEmpty() {
if(top == -1)
return true;
else
return false;
}
void Push(int stack[], int data){
top++; // top을 증가시키고
stack[top] = data; // 그 위치에 data를 저장
}
int Pop(int stack[]) {
int idx;
if(IsEmpty()) {
printf("Stack Memory Error!");
exit(-1);
}
idx = top; // 임시변수 idx에 먼저 top값을 저장하고
top--; // top을 감소시키고
return stack[idx]; // stack에서 top의 위치에 있었던(idx에 있는) 값을 반환
}
int Peek(int stack[]) {
if(IsEmpty()) {
printf("Stack Memory Error!");
exit(-1);
}
return stack[top];
}
int main(void){
int stack[5] = {0,};
StackInit(); // Stack의 초기화
// 데이터 넣기
Push(stack, 1); Push(stack, 2); Push(stack, 3);
Push(stack, 4); Push(stack, 5); Push(stack, 6);
// 데이터 보기
cout << "Peek : " << Peek(stack) << endl;
// 데이터 꺼내기
cout << "Pop : ";
while(!IsEmpty())
cout << Pop(stack);
cout << endl;
cout << "Peek : " << Peek(stack) << endl;
return 0;
}간단하게 int형 데이터를 저장하는 배열 기반의 스택을 구현해 보았다. stack을 먼저 초기화 준 다음, Push를 통해 int형 값을 저장한다. 그리고 Peek으로 맨 위의 값을 확인해 보면 6이 출력된다. 이제 Pop연산을 스택이 비워질 때 까지 반복한 다음, 다시 Peek을 해보면 IsEmpty가 false일 것이므로 에러문이 출력되는 것을 알 수 있다.
Peek : 6
Pop : 654321
Stack Memory Error!
연결 리스트 기반의 스택 구현
스택을 연결 리스트로 구현하는 것은 연결 리스트에서 새로운 노드를 꼬리(tail)가 아닌 머리(head)에 추가하는 형태이다. 하지만 비교적으로 배열 기반으로 구현하는 것에 비해 복잡하므로, 실제 알고리즘 문제 풀이에서는 거의 사용하지 않는다.
연결 리스트 기반의 스택도 그냥 연결 리스트이다. 다만 저장된 순서의 역순으로 조회(삭제)가 가능한 연결 리스트일 뿐이다.
2. 스택을 활용한 문제풀이
실제 문제에서는 스택을 구현하여 사용하는 경우는 드물다. 대부분 기존의 라이브러리에 포함된 스택을 활용하거나, 스택의 동작원리만을 응용하여 해결한다. C++와 JAVA에서는 stack 라이브러리에 포함되어있고, Python에서는 List를 활용하면 된다. 앞 서 말한 것과 같이, 스택은 맨위의 값을 제외하고 안에 무엇이 들어있는지 볼 수 없다. 따라서 만약 문제를 풀다가 그러한 상황이 생긴다면, 그것은 스택을 사용하면 안되는 상황이다.
BOJ 10828. 스택
먼저, 문제에서 주어진 5가지 스택의 기본기능을 구현한다. 그리고 문제에서 주어진 입력의 양식에 맞추어서 main함수를 구현한다. N을 입력받고 N번만큼 반복하면서 각 명령어에 해당하는 스택연산 함수를 호출하도록 하면 해결된다.
- push X: 정수 X를 스택에 넣는 연산이다.
- pop: 스택에서 가장 위에 있는 정수를 빼고, 그 수를 출력한다. 만약 스택에 들어있는 정수가 없는 경우에는 -1을 출력한다.
- size: 스택에 들어있는 정수의 개수를 출력한다.
- empty: 스택이 비어있으면 1, 아니면 0을 출력한다.
- top: 스택의 가장 위에 있는 정수를 출력한다. 만약 스택에 들어있는 정수가 없는 경우에는 -1을 출력한다
직접 스택 구현
#include <iostream>
#include <string>
#define STACK_SIZE 10000
using namespace std;
struct Stack { // 구조체로 Stack을 정의
int data[STACK_SIZE];
int size; // top index
Stack() {
size = -1;
}
void push(int num) {
data[++size] = num; // top 인덱스를 -1로 시작했으므로 선위증가
}
bool isEmpty() {
if (size == -1) {
return true;
} else {
return false;
}
}
int pop() {
if (isEmpty()) {
return -1;
} else {
int tmp = size;
size--;
return data[tmp];
}
}
int top() { // peek
if (isEmpty()) {
return -1;
} else {
return data[size];
}
}
};
int main() {
int N; cin >> N; Stack s;
while (N--) {
string command; cin >> command;
if (command == "push") {
int num; cin >> num;
s.push(num);
} else if (command == "top") {
cout << s.top() << '\n';
} else if (command == "size") {
cout << s.size+1 << '\n';
} else if (command == "empty") {
cout << s.isEmpty() << '\n';
} else if (command == "pop") {
cout << s.pop() << '\n';
}
}
return 0;
}가장 기본적인 방법으로 구현한 코드이다. 하지만 구조체를 사용하므로 실행시간은 단순 일차원 배열에 비해 다소 느리다. 또한, 아래와 같이 C++의 stack 라이브러리를 사용할 수도 있다. 이 라이브러리에는 위에서 직접 정의한 push, pop, size, empty와 같은 함수는 기본적으로 포함되어 있다.
C++ 라이브러리 사용
#include <iostream>
#include <stack>
#include <string>
using namespace std;
int main() {
int n; cin >> n;
stack<int> s;
while (n--) {
string cmd; cin >> cmd;
if (cmd == "push") {
int num; cin >> num;
s.push(num);
} else if (cmd == "top") {
cout << (s.empty() ? -1 : s.top()) << '\n';
} else if (cmd == "size") {
cout << s.size() << '\n';
} else if (cmd == "empty") {
cout << s.empty() << '\n';
} else if (cmd == "pop") {
cout << (s.empty() ? -1 : s.top()) << '\n';
if (!s.empty()) {
s.pop();
}
}
}
return 0;
}
C 스타일의 단순배열 사용 코드
#include <stdio.h>
#include <string.h>
#define STACK_SIZE 10000
int N, top = -1, stack[STACK_SIZE];
int empty() {
if (top == -1) return 1;
else return 0;
}
void push(int x) {
stack[++top] = x;
}
int pop() {
if (empty()) return -1;
return stack[top--];
}
int size() {
return top + 1;
}
int peek() {
if (empty()) return -1;
return stack[top];
}
int main() {
int data;
char opcode[20];
scanf("%d", &N);
for (int i = 0; i < N; i++) {
scanf("%s", opcode);
if (!strcmp(opcode, "push")) {
scanf("%d", &data);
push(data);
}
else if (!strcmp(opcode, "pop")) printf("%d\n", pop());
else if (!strcmp(opcode, "size")) printf("%d\n", size());
else if (!strcmp(opcode, "top")) printf("%d\n", peek());
else if (!strcmp(opcode, "empty")) printf("%d\n", empty());
}
return 0;
}위와 같이 단순 일차원 배열로 스택을 구현하여 풀이하면 실행시간이 가장 빠르다.

