해싱(hashing)
키 값에 대한 산술적 연산에 의해 테이블의 주소를 계산하여 항목에 접근
해시 테이블(hash table)
키 값의 연산에 의해 직접 접근이 가능한 구조
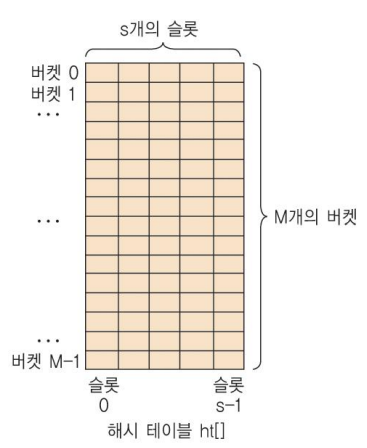
해시 테이블의 구조
- M개의 버켓(bucket)으로 구성된 테이블
- ht[0], ht[1], ..., ht[M-1]의 원소를 ㅏㄱ짐
- 하나의 버켓에 s개의 슬롯(slot) 가능
충돌(collision)
- 서로 다른 두 개의 탐색키 k1과 k2에 대하여 h(k1) = h(k2)인 경우
오버플로우(overflow)
- 충돌이 버켓에 할당된 슬롯 수보다 많이 발생하는 것
- 오버플로우 해결 방법 반드시 필요
해시 함수(hash function)
- 탐색키를 입력받아 해시 주소(hash address) 생성
- 이 해시 주소가 배열로 구현된 해시 테이블의 인덱스
좋은 해시 함수의 조건
- 충돌이 적어야 한다
- 해시함수 값이 해시테이블의 주소 영역 내에서 고르게 분포되어야 한다
- 계산이 빨라야 한다
해시 함수 종류
[ 제산 함수 (나머지 연산자 사용) ]
h(k) = k mod M
해시 테이블의 크기 M은 소수(prime number) 선택
[ 폴딩 함수 (접지 함수) ]
이동 폴딩(shift folding)
탐색 키를 여러 부분으로 나눈값들을 더하여 해시 주소를 얻음
경계 폴딩(boundary folding)
탐색키의 이웃한 부분을 거꾸로 더하여 해시 주소를 얻음
[ 중간제곱 함수 ]
탐색키를 제곱한 다음, 중간의 몇 비트를 취해서 해시 주소 생성
[ 비트추출 함수 ]
탐색키를 이진수로 간주하여 임의의 위치의 k의 개의 비트를 해시 주소로 사용
[ 숫자 분석 방법 ]
키 중에서 편중되지 않는 수들을 해시테이블의 크기에 적합하게 조합하여 사용
충돌해결책
충돌(collision)
서로 다른 키를 갖는 항목들이 같은 해시 주소를 가지는 현상
충돌이 발생하면 오버플로우 발생
오버플로우를 효과적으로 해결하는 방법 필요
오버플로우 해결책
선형조사법(linear probing)
충돌이 일어난 항목을 해시 테이블의 다른 위치에 저장
체이닝(chaining)
각 버켓에 삽입과 삭제가 용이한 연결 리스트 할당
선형조사법(linear probing)
충돌이 ht[k]에서 발생했다면,
- ht[k+1]이 비어있는지 조사
- 만약, 비어있지 않다면 ht[k+2] 조사
- 비어있는 공간이 나올 때까지 계속 조사
- 테이블의 끝에 도달하게 되면 다시 테이블의 처음부터 조사
- 조사를 시작했던 곳으로 다시 되돌아오게 되면 테이블이 가득 찬 것임
군집화(Clustering) 문제 발생
- 한번 충돌이 발생하면 그 위치에 항목들이 집중되는 현상
- 탐색 시간을 증가시킴
이차 조사법(quadratic probing)
선형조사법과 달리 이차 함수에 의해 이동 폭을 넓혀 가면서 사용
(h(k)+inc^2 mod M) for inc=0, 1, ..., M-1
- 선형 조사법에서의 문제점인 군집화 크게 완화 가능
이중해싱법(double hashing)
- 선형 조사와 이차 조사에서, 해시 함수가 같은 값이 나오면 동일한 형태로 빈 공간을 찾으므로, 같은 값이 많이 발생하는 해시 함수일 경우에는 잦은 충돌이 발생
재해싱(rehashing) 이라고도 하며, 오버플로우가 발생하면 원 해시함수와 다른 별개의 해시 함수 사용
step = C-(k mod C) -> 1에서 C사이의 값을 생성
h(k), (h(k) + step) % M, (h(k) + 2*step) % M, ...
체이닝(chaining)
오버플로우 문제를 연결 리스트로 해결
- 각 버켓에 고정된 슬롯이 할당되어 있지 ㅇ낳음
- 각 버켓에, 삽입과 삭제가 용이한 연결 리스트 할당
- 버켓 내에서는 연결 리스트 순차 탐색
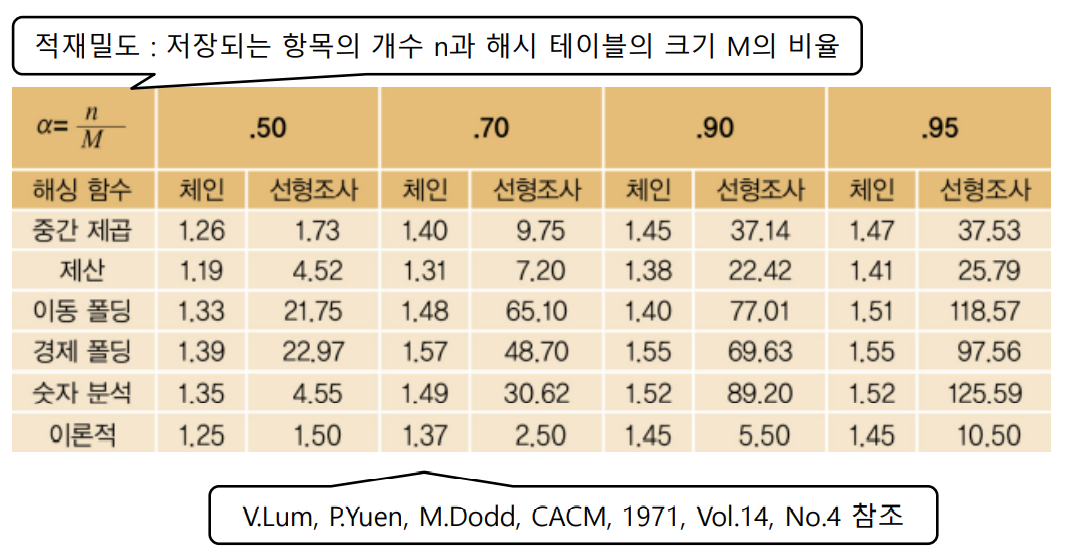
해싱의 성능분석
각 알고리즘에 따른 평균 버켓 접근 수