0. 인트로
우리는 핸드폰으로 지하철 노선 검색을 한다. 카X오 지하철 어플을 실행하면 경로 찾기 기능이 있다. 그런데 경로 찾는 방법에 최소 환승과 최단거리 두가지의 탭이 있는 것을 알 수 있다. 지하철 역을 각각의 정점(노드)라고 했을 때 지하철 노선도도 자료구조의 그래프에 해당이 된다. 정점 간 연결이 되어 있는 형태이기 때문이다. 이 포스트에서는 그래프를 이용하여 검색을 하는 알고리즘에 대하여 알아볼 것이다.
1. 그래프 검색 알고리즘: BFS와 DFS
1. BFS
BFS는 Breadth-First Search의 약자로 너비 우선 검색이라는 뜻이다. 가까운 정점부터 탐색한 다음에 더는 탐색할 정점이 없을 때, 그 다음 떨어져 있는 정점을 순서대로 방문하는 방식이다. 너비 우선 검색은 주로 두 정점 사이의 최단 경로를 찾을 때 사용된다. BFS는 코드를 작성할 때, 큐(Queue)를 응용한다. 큐 자료구조를 쓸 때와 마찬가지로 while 반복문을 이용한다.
2. DFS
DFS는 Depth-First Search의 약자이다. 다시 말해, BFS는 깊이 우선 탐색이라는 뜻이며, 다른 연결을 방문하기 전에 하나의 연결을 깊게 파고들면서 순회하는 검색 알고리즘이다. 트리에서 트리 순회가 DFS 방식이다. 깊이 우선 방식은 코드를 작성할 때, 재귀를 이용한다.
2. BFS / DFS 예제: 연결된 정점들 찾기
0. 전체적인 함수 작성
방향이 없는 간선들의 목록이 주어질 때, 연결된 정점의 컴포넌트(그룹들)가 몇 개인지 반환하는 함수를 작성하는 문제가 있다고 하자. 이 함수의 인자는 edges 뿐이다. edges에는 2차원 Array 형식이다. 그리고 각각의 요소는 시작과 도착 정점이 담겨있는 배열이다. 만약 edges가 [[0, 1], [1, 2], [3, 4]]라고 한다면, 아래 그림과 같은 그래프 형식일 것이다.
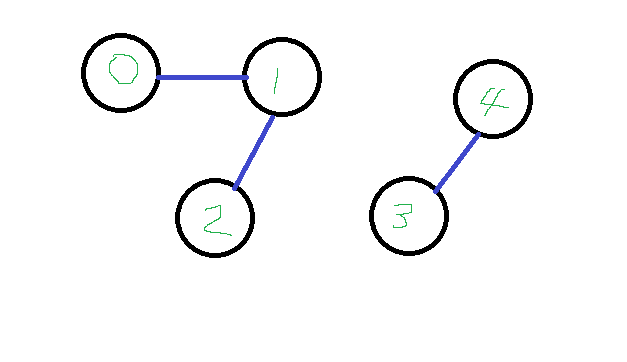
주어진 edge를 이용하여 인접 리스트를 만들어 볼 것이다. 물론 인접 행렬을 만들고 해결해도 된다. 인접 리스트를 만들기 위하여 edges 2차원 배열에서 최대값을 찾는다. 아래는 2차원 배열에서 최대값을 찾는 코드이다. 배열 고차함수 reduce를 사용하면 간단하게 해결 가능하다.
// Find the maximun of Vertices
const maxVertex = edges.reduce((a,c) => {
const bigger = Math.max(...c);
if (bigger > a) return bigger;
return a;
}, 0);그리고 인접 리스트를 생성한다.
const adjList = {};
// adjList를 만들고 maxVertex만큼 반복시켜준다.
for (let i = 0; i <= maxVertex; i++) {
adjList[i] = [];
};
// edges를 순회하면서 간선을 연결해준다.(인접 리스트이기 때문에 값을 push함)
for (let i = 0; i < edges.length; i++) {
adjList[edges[i][0]].push(edges[i][1]);
adjList[edges[i][1]].push(edges[i][0]);
}정점을 순회할 것이기 때문에 방문한 정점들을 담을 객체를 선언한다. 그리고 컴포넌트가 몇개인지 세줄 변수를 따로 선언해준다. count로 해줄 것이다. 이 상태에서 그래프에 있는 vertex를 전부 순회할 것이다. 만약에 정점을 순회하면서 순회하지 않은 정점을 만났을 때에만, BFS를 이용하여 순회해준다. 그리고 동시에 count를 세준다. 반복이 끝나면 count를 리턴해준다. 아래는 코드이다.
// 방문한 버텍스를 담을 객체를 선언합니다.
const visited = {};
// 컴포넌트가 몇 개인지 카운트할 변수를 선언합니다.
let count = 0;
// 그래프에 있는 버텍스를 전부 순회합니다.
for (let vertex = 0; vertex <= maxVertex; vertex++) {
// 만약 i 번째 버텍스를 방문하지 않았다면 bfs로 해당 버텍스와, 버텍스와 연결된(간선) 모든 버텍스를 방문합니다.
// BFS로 갈 수 있는 모든 정점들을 방문하며 visited에 담기 때문에, 방문한 버텍스는 visited에 들어 있어서 bfs를 돌지 않습니다.
// 이렇게 컴포넌트를 확인합니다.
if (!visited[vertex]) {
// 그래프와 버텍스, 방문했는지 확인할 visited를 변수에 담습니다.
bfs(adjList, vertex, visited); // bfs 이용
// dfs(adjList, vertex, visited); // dfs 이용시
// 카운트를 셉니다.
count++;
}
}
// 카운트를 반환합니다.
return count;
코드를 짜기는 했는데 문제는 bfs 함수에 대하여 정의하지 않았다는 것이 문제이다. 이대로 코드를 짠다면 'Reference Errer: bfs is not found'가 무조건 뜬다. 따라서 bfs 함수를 정의해야 한다.
1. BFS를 이용한 풀이
bfs는 앞서 말했듯이 queue를 활용한다. 그리고 queue는 반복문과 친구이다. queue를 이용한 문제풀이는 queue 배열을 선언하고, queue 배열의 크기가 0 이상일 때에만 반복시키는 것이 핵심이다. 즉, 줄 서기가 끝나면 반복은 끝내면 된다. 아래는 코드이다.
// bfs solution
function bfs(adjList, vertex, visited) {
// bfs는 가장 가까운 정점부터 탐색하기 때문에 queue를 사용합니다.
// queue에 vertex를 담습니다.
const queue = [vertex];
// 해당 버텍스를 방문했기 때문에 visited에 담아 주고, 방문했다는 표시인 true를 할당합니다.
visited[vertex] = true;
// queue의 길이가 0일 때까지 순환합니다.
while (queue.length > 0) {
// cur 변수에 정점을 할당합니다.
// queue는 선입선출이기 때문에 shift 메소드를 사용하여 버텍스를 가져옵니다.
const cur = queue.shift();
// 그래프의 cur 정점에 있는 간선들을 전부 순회합니다.
for (let i = 0; i < adjList[cur].length; i++) {
// 만약, 해당 버텍스를 방문하지 않았다면 queue에 삽입합니다.
// 방문했다는 표시로 visited에 해당 버텍스를 삽입하고 true를 할당합니다.
if (!visited[adjList[cur][i]]) {
queue.push(adjList[cur][i]);
visited[adjList[cur][i]] = true;
}
// queue에 다음으로 방문할 버텍스가 있기 때문에 while은 멈추지 않습니다.
// 만약, queue가 비어 있다면 더 이상 갈 곳이 없는 것이기 때문에 bfs 함수를 종료하고 카운트를 셉니다.
}
}
}2. DFS를 이용한 풀이
아래는 DFS를 이용한 풀이이다. DFS는 재귀와 함께 따라다닌다. 아래는 코드이다.
// dfs solution
function dfs(adjList, vertex, visited) {
// 해당 버텍스에 방문했다는 표시로 visited key에 vertex를 담고 값에 true를 할당합니다.
visited[vertex] = true;
// 해당 버텍스의 모든 간선들을 전부 순회합니다.
for (let i = 0; i < adjList[vertex].length; i++) {
// 만약 i번째 간선과 이어진 버텍스를 방문하지 않았다면
if (!visited[adjList[vertex][i]]) {
// dfs를 호출해(재귀) 방문합니다.
dfs(adjList, adjList[vertex][i], visited);
}
// 모든 방문이 종료되면 다음 버텍스를 확인합니다.
// 재귀가 종료되면(한 정점에서 이어진 모든 간선들을 확인했다면) dfs 함수를 종료하고 카운트를 셉니다.
}
}