[JavaScript] 자료구조 (4): 트리 & 이진 트리 검색

0. 인트로

드디어 기조 자료 구조 중에서 가장 어렵다고 느껴지는 트리에 대하여 설명하고자 한다. 트리 구조가 무엇인지 설명할 것이며, 특히 이진 트리도 같이 언급할 것이다.

1. 트리 구조란?

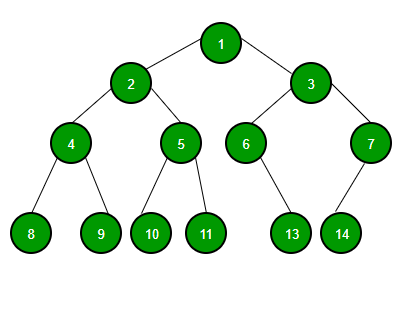
트리 구조는 맨 위의 사진과 같이 하나의 뿌리로부터 시작되어서 가지가 여러 갈래로 뻗어있는 자료 구조를 말한다. 트리 구조가 어디서 많이 봤다고 하면 착각은 아니다. 스포츠를 좋아하는 사람이라면 많이 봤을 것이라고 생각되는 토너먼트 대진표도 트리 구조이다. 아래서부터 차례로 올라가서 가장 꼭대기까지 가는 것이 토너먼트이다. 트리구조는 반대로 위의 뿌리 노드부터 시작해서 아래로 내려가는 구조다. 이쯤에서 트리 구조에서 나오는 주요 용어를 정리해보겠다.

2. 트리 용어 정리

• 노드(Node) : 트리 구조를 이루는 모든 개별 데이터

• 루트(Root) : 트리 구조의 시작점이 되는 노드

• 부모 노드(Parent node) : 두 노드가 상하관계로 연결되어 있을 때 상대적으로 루트에서 가까운 노드

• 자식 노드(Child node) : 두 노드가 상하관계로 연결되어 있을 때 상대적으로 루트에서 먼 노드

• 리프(Leaf) : 트리 구조의 끝지점이고, 자식 노드가 없는 노드

위의 사진을 기준으로 하면 1번 노드가 루트 노드가 된다. 그리고 2번과 3번 노드는 서로 형제 관계이다. 그리고 2번 노드와 4,5번 노드는 각각 부모와 자식 노드가 된다. 맨 밑의 8번 라인에 있는 노드(9, 10, 11, 13, 14번)는 리프(잎사귀) 노드라고 한다. 한편, 밑에 있는 용어들도 자주 쓰이니 따로 정리해보았다.

• 깊이: 계층이 얼마나 밑에 있는지를 나타내는 척도. 단 뿌리 노드는 깊이가 0이다.

• 레벨: 트리 구조에서 같은 깊이를 가진 노드를 묶은 것. 뿌리 노드부터 1부터 시작함.

• 높이: 리프 노드를 기준으로 해당 노드까지 떨어진 정도

• 서브 트리: 큰 트리 안에서 비슷한 트리 구조를 가진 작은 트리

위의 트리 구조를 예를 들면, 2번과 3번은 깊이와 레벨, 높이는 각각 1, 2, 2이다.

3. 이진 트리와 이진 검색 트리

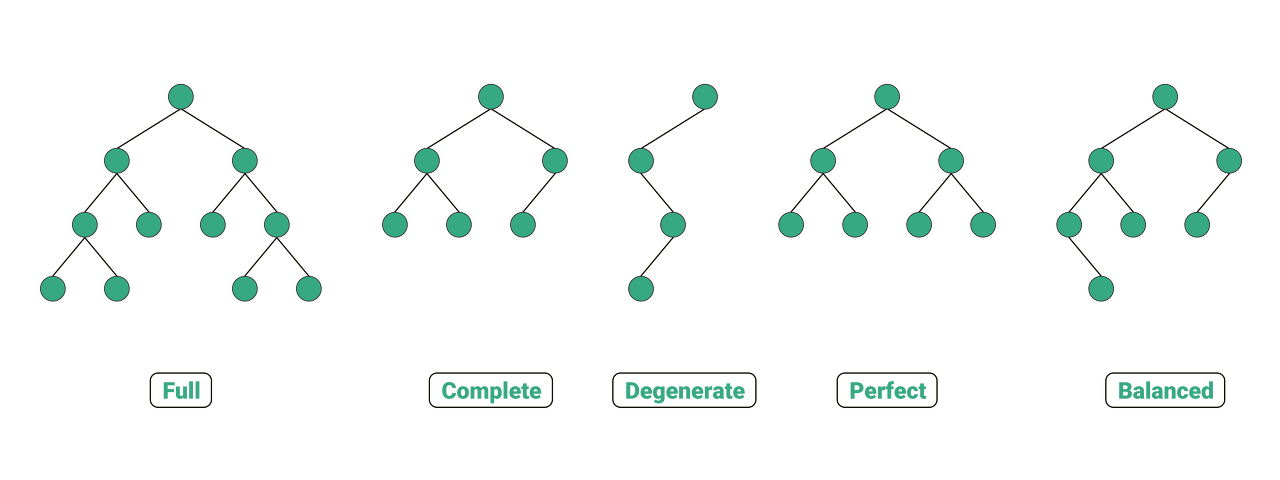
이진 트리는 트리 구조 중 특수한 경우로, 자식 노드가 두개인 트리를 뜻한다. 자식 노드가 두개이기 대문에 자식 노드는 왼쪽 or 오른쪽으로 구분할 수 있다. 한편, 이진 트리는 자료의 삽입, 삭제 방법에 따라 정 이진 트리(Full binary tree), 완전 이진 트리(Complete binary tree), 포화 이진 트리(Perfect binary tree)로 나뉜다. 아래는 예시이다.

• 정 이진 트리: 각 노드가 0 개 혹은 2 개의 자식 노드를 갖는 경우

• 완전 이진 트리: 마지막 레벨을 제외한 모든 노드가 가득 차 있어야 하고, 마지막 레벨의 노드는 전부 차 있지 않아도 되지만 왼쪽이 채워져 있는 경우

• 포화 이진 트리: 정 이진 트리이면서 완전 이진 트리인 경우. 모든 리프 노드의 레벨이 동일하고, 모든 레벨이 가득 채워져 있어야 됨.

이진 검색 트리는 이진 트리를 이용한 검색 방법을 이용할 때 쓰는 트리구조이다.
이진 탐색 트리(Binary Search Tree)는 모든 왼쪽 자식의 값이 루트나 부모보다 작고, 모든 오른쪽 자식의 값이 루트나 부모보다 큰 값을 가지는 특징이 있다. 이진 검색 트리를 쓰면 검색에 필요한 시간을 줄일 수 있다. 시간복잡도가 O(N)에서 O(log_2(N))으로 줄어들기 때문이다.
만약에 1부터 10까지 있는 숫자 배열이 있을 때 9이라는 숫자를 찾는다고 가정하자. 그냥 막무가내로 찾는다면 배열을 앞에서부터 찾는다고 가정했을 경우, 9번째가 되어서야 나온다.(만약 10을 찾는다면...) 하지만 이진 트리를 사용한다면 최대 3번이면 끝난다. 이진트리를 사용하는 검색 메소드는 이분법(방정식의 해를 범위를 반으로 줄여나가면서 푸는 알고리즘)과 유사하기 때문이다. 1에서 10까지의 배열 [1,2,3,4,5,6,7,8,9,10]이 있을 때 중간값을 구한다. 중간값은 5.5이기 때문에 5.5를 기준으로 반을 소거시킨다. 그러면 [6,7,8,9,10]의 중간값인 8을 기준으로 또 소거시킨다.(만약 찾는 값이 8이면 여기서 끝) 중간값 8을 소거시시켰으면 나머지 요소인 [9,10] 중에 찾으면 검색이 끝난다. 그냥 막무가내로 앞에서부터 찾는 것보다 문제 해결 시간이 훨씬 단축되는 것을 알 수 있다.

4. 트리 순회 알고리즘

특정 목적을 위해 트리의 모든 노드를 한 번씩 방문하는 것을 트리 순회(Tree traversal)라고 한다. 윗 문단에서 숫자 9를 찾기 위하여 중간값을 조회하고 자르고의 과정을 반복했다. 이러한 과정도 일종의 트리 순회이다. 트리 노드를 순회하는 방법은 루트 노드를 언제 거치느냐에 따라서 세 가지로 나뉜다(전위 순회, 중위 순회, 후위 순회). 트리를 순회할 때에는 항상 왼쪽이 우선이다!(이거는 큰 형님들 끼리의 약속입니다. 까라면 깝시다)

• 전위 순회: 루트에서 시작해 왼쪽의 노드들을 순차적으로 둘러본 뒤, 왼쪽의 노드 탐색이 끝나면 오른쪽 노드를 탐색을 하는 방식. 위의 트리라면, 1->2->4->8->9->5->10->11->3->6->13->7->14

• 중위 순회: 제일 왼쪽 끝에 있는 노드부터 순회하기 시작하여, 루트를 기준으로 왼쪽에 있는 노드의 순회가 끝나면 루트를 거쳐 오른쪽에 있는 노드로 이동하여 마저 탐색하는 방식. 8->4->9->2->10->5->11->1->13->6->3->14->7

• 후위 순회: 제일 왼쪽 끝에 있는 노드부터 순회하기 시작하여, 루트를 거치지 않고 오른쪽으로 이동해 순회한 뒤, 제일 마지막에 루트를 방문하는 방식. 8->9->4->10->11->5->2->13->6->14->7->3->1

5. 트리 구현하기

아래는 클래스로 트리를 구현한 것이다.

class Tree {
  constructor(value) {
		// constructor로 만든 객체는 트리의 Node가 됩니다.
    this.value = value;
    this.children = [];
  }

	// 트리의 삽입 메서드를 만듭니다.
  insertNode(value) {
		// 값이 어떤 이름으로 만들어지고 어느 위치에 붙는지 떠올리는 것이 중요합니다.
		// TODO: 트리에 붙게 될 childNode를 만들고, children에 넣어야 합니다.
    const childNode = new Tree(value);
    this.children.push(childNode);
  }

	// 트리 안에 해당 값이 포함되어 있는지 확인하는 메서드를 만듭니다.
  contains(value) {
		// TODO: 값이 포함되어 있다면 true를 반환하세요. 
    if (this.value === value) {
      return true;
    }
		// TODO: 값을 찾을 때까지 children 배열을 순회하며 childNode를 탐색하세요.
    for (let i=0;i<this.children.length;i++) {
      const childNode = this.children[i];
      if (childNode.contains(value)) {
        return true;
      }

    }
	
		// 전부 탐색했음에도 불구하고 찾지 못했다면 false를 반환합니다.
    return false;
  }
}

6. 이진 검색 트리 구현하기

class BinarySearchTree {
    //BST의 constructor를 구현합니다.
    constructor(value) {
      this.value = value;
      this.left = null;
      this.right = null;
    }
    // tree에 value를 추가합니다.
    insert(value) {
      // 인자의 value가 this.value보다 작을 경우, 왼쪽 노드에서 진행합니다.
      if (value < this.value) {
        // this.left에 아무것도 없을 경우, 새로운 자식 노드를 추가합니다.
        if (this.left === null) {
          this.left = new BinarySearchTree(value);
        }
        // this.left의 자식 노드가 있을 경우, 자식 노드에서 insert 재귀를 사용합니다.
        else {
          this.left.insert(value);
        }
      }
      // 인자의 value가 this.value보다 클 경우, 오른쪽 노드에서 진행합니다.
      else if (value > this.value) {
        // this.right에 아무것도 없을 경우, 새로운 자식 노드를 추가합니다.
        if (this.right === null) {
          this.right = new BinarySearchTree(value);
        }
        // this.left의 자식 노드가 있을 경우, 자식 노드에서 insert 재귀를 사용합니다.
        else {
          this.right.insert(value);
        }
      } else {
        // 이미 value값을 포함하고 있습니다.
      }
    }
    // tree의 value값을 탐색합니다.
    contains(value) {
      // 찾는 value값이 노드의 value와 일치한다면, true를 리턴합니다.
      if (value === this.value) {
        return true;
      }
      // 찾는 value값이 노드의 value 보다 작다면, 왼쪽에서 contains의 재귀를 진행합니다.
      if (value < this.value) {
        return !!(this.left && this.left.contains(value));
      }
      // 찾는 value값이 노드의 value 보다 크다면, 오른쪽에서 contains의 재귀를 진행합니다.
      if (value > this.value) {
        return !!(this.right && this.right.contains(value));
      }
    }
    //tree를 전위 순회 합니다.
    preorder(callback) {
      callback(this.value);
      if (this.left) {
        this.left.preorder(callback);
      }
      if (this.right) {
        this.right.preorder(callback);
      }
    }
    // tree를 중위 순회 합니다
    inorder(callback) {
      if (this.left) {
        this.left.inorder(callback);
      }
      callback(this.value);
      if (this.right) {
        this.right.inorder(callback);
      }
    }
    //tree를 후위 순회 합니다
    postorder(callback) {
      if (this.left) {
        this.left.postorder(callback);
      }
      if (this.right) {
        this.right.postorder(callback);
      }
      callback(this.value);
    }
  }