서론

• FIR(유한 임펄스 응답)
  필터의 길이가 한정적이고 설계가 쉬우며, 신호를 쉽게 처리할 수 있다. 영상처리에서는 FIR을 주로 사용한다.

• IIR(무한 임펄스 응답)
  필터의 길이가 무한하며 필터의 특성이 좋다. 하지만 설계가 어렵고, 신호를 처리하기 힘들다.

• Offset
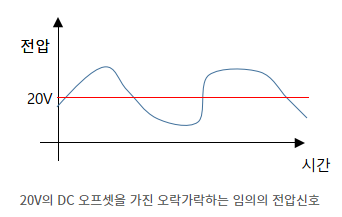
  일반적인 교류 신호는 0을 중심으로 상하 같은 전압으로 움직인다. 예를 들어 교류 신호 1V의 경우 0을 중심으로 +1V~-1V 사이를 움직인다. 만약 여기서 1V의 DC(직류)성분을 더하면 0~2V 사이를 움직이게 된다. 이와 같은 개념을 DC Offset이라고 하고 위의 예에서 DC Offset은 1이다. DC Offset을 제거하는 방법으로는 HPF를 통과시키는 방법이 있다.
  

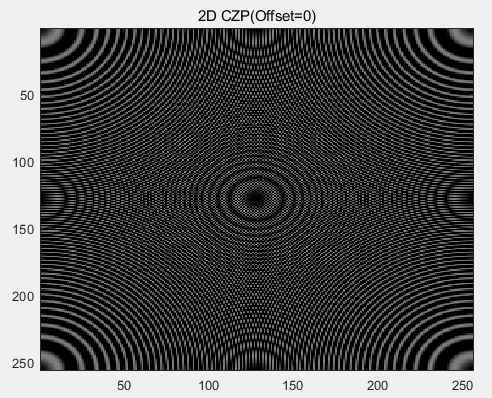
2D CZP이미지를 통해 Offset을 확인해보았다.

CZP 이미지란 변화가 높은 중심(고주파 영역)에서 각모서리(저주파 영역)을 잘 나타낸 이미지로 검증할때 유용히 사용함.

Offset = 0

Offset = 128일 경우 없는 경우에 비해 밝은 것을 확인했다.

필터의 주파수 응답과 Group Delay_LPF

2차원 LPF 또한 1차원 LPF와 동일한 개념을 가지고 있다. 아래 그림11은 1차원 필터 계수인 LPF=[1 2 1]을 가지고 X 축으로 한번 Y 축으로 한번 통과시켜 2차원의 필터 계수를 만든 것이다. 1차원 필터를 이용하여 2차원 필터를 만들 때는 X축과 Y축의 곱으로 나타내면 된다. 그림11의 필터 계수의 총 합은 1이다.

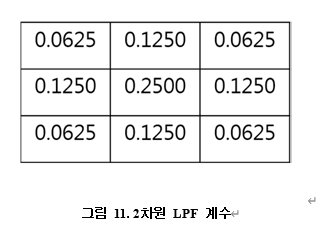
그림11의 필터계수를 이용하여 주파수 응답과 Group Delay를 2D 그래프로 나타낸 것이다. 주파수 응답을 살펴보면 1차원 LPF와 비슷한 형태를 띄고 있고, 저주파를 통과시킨다는 것을 알 수 있다. 또한 필터 계수는 총 9개이며 Group Delay는 모든 주파수에서 4인 것을 확인할 수 있다. 이는 필터를 통과하였을 때 4만큼의 지연이 발생한다는 것을 의미한다.


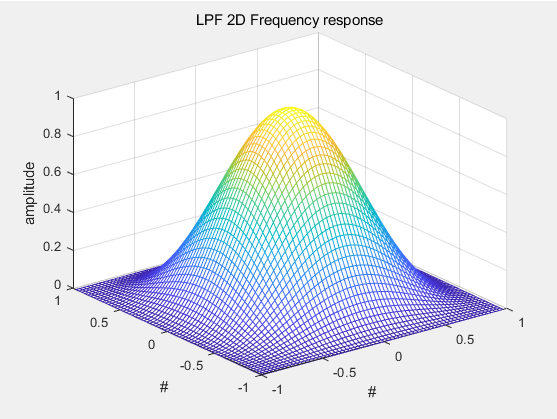
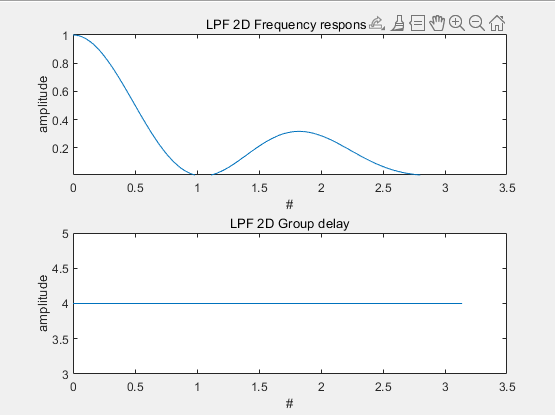
2차원 LPF의 주파수 응답 3D

2D CZP Filtering_LPF

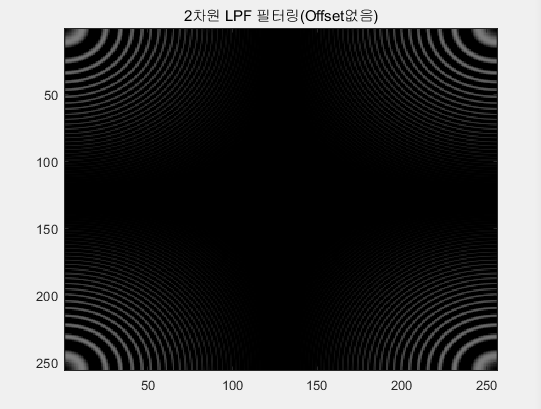
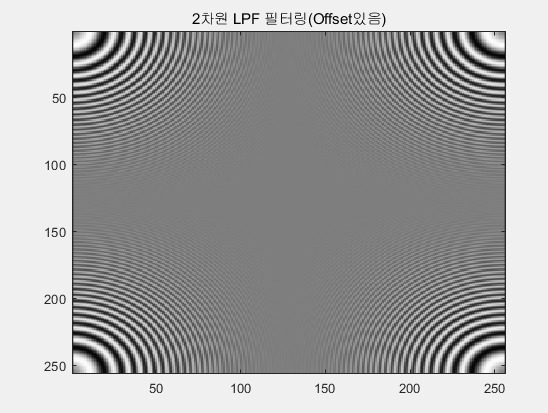
필터계수를 이용하여 Offset이 없는 경우와 있는 경우 각각의 CZP를 필터링한 것이다. 우선 Offset이 없는 경우 필터를 통과한 데이터의 범위는 필터를 통과하기전 데이터 범위와 동일하게 -128~127 사이의 값을 가진다. Offset이 있는 경우도 데이터의 범위는 변하지 않아 0~255 사이의 값을 가진다. 따라서 Offset이 없는 경우의 이미지는 여전히 어둡고 Offset이 있는 경우의 이미지는 여전히 밝은 색을 띄고 있다.

필터의 주파수 응답과 Group Delay_HPF

1차원 HPF
2차원 HPF 또한 1차원 HPF와 동일한 개념을 가지고 있다. 아래 그림 은 1차원 필터 계수인 HPF=[-1 2 -1]을 가지고 X 축으로 한번 Y 축으로 한번 통과시켜 2차원의 필터 계수를 만든 것이다. 1차원 필터를 이용하여 2차원 필터를 만들 때는 X축과 Y축의 곱으로 나타내면 된다.

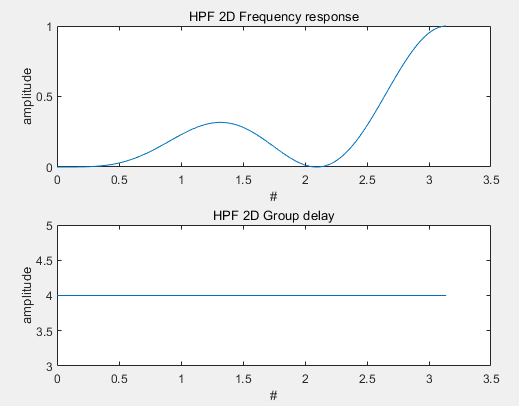
필터계수를 이용하여 주파수 응답과 Group Delay를 2D 그래프로 나타낸 것이다. 주파수 응답을 살펴보면 1차원 HPF와 비슷한 형태를 띄고 있고, 고주파를 통과시킨다는 것을 알 수 있다. 또한 위의 2차원 LPF와 동일하게 필터 계수는 총 9개이며 Group Delay 또한 모든 주파수에서 4인 것을 확인할 수 있다. 이는 필터를 통과하였을 때 4만큼의 지연이 발생한다는 것을 의미한다.

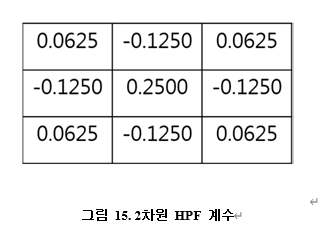
그림15의 필터 계수의 총 합은 0이므로 일정하거나 서서히 변하는 밝기 영역에서는 필터의 응답이0에 가깝다. 따라서 이 필터를 통과한 결과 영상에서는 저주파 성분의 화소를 검은색으로 출력한다. 필터 계수 중앙의 큰 양수 값과 주위의 작은 음수 값으로 구성되어 경계선이 더욱 두드러지고 경계선은 흰색에 가까운 밝은 색으로 나타난다.


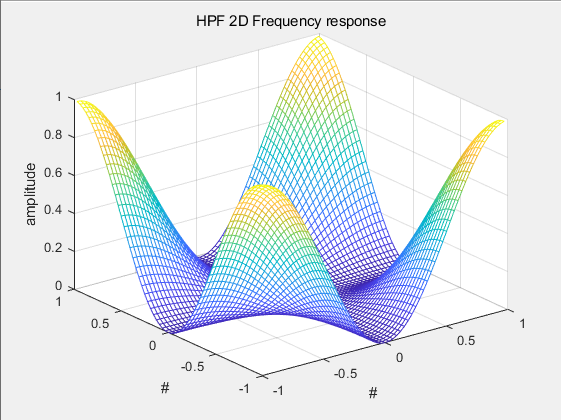
2차원 LPF의 주파수 응답 3D

2D CZP Filtering_HPF

필터계수를 이용하여 Offset이 없는 경우와 있는 경우 각각의 CZP를 필터링한 것이다. 우선 Offset이 없는 경우 필터를 통과한 데이터의 범위는 필터를 통과하기전 데이터 범위와 동일하게 -128~127 사이의 값을 가진다. Offset이 있는 경우는 필터를 통과하기전 0~225 사이의 데이터 값이 필터를 통과하고 나면 Offset 성분이 사라져 -128~127의 데이터 범위를 가지게 된다. 따라서 HPF는 DC Offset을 제거하는 기능을 가지고 있고, 이를 그림18을 통해 확인할 수 있다. 결국 Offset이 있든 없든 HPF를 통과하면 결과는 모두 Offset이 제거되어 동일하게 나온다.

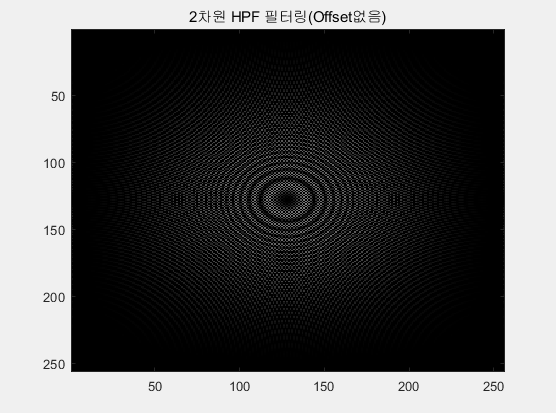
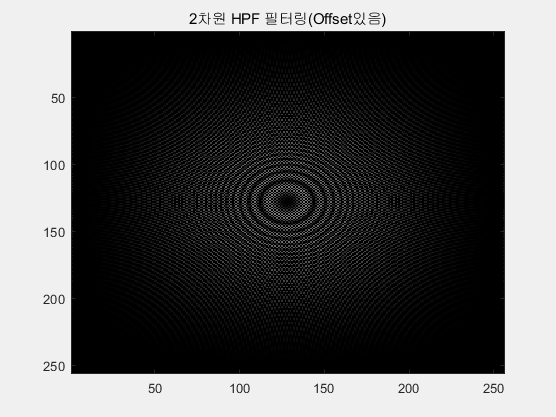
1차원 필터링

LPF 필터링 결과

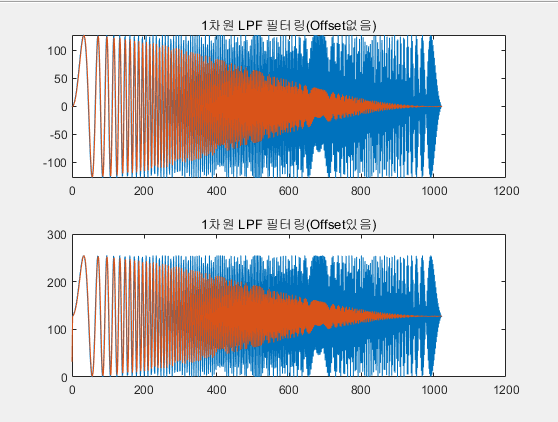
offset을 제거하지 않음

HPF 필터링 결과

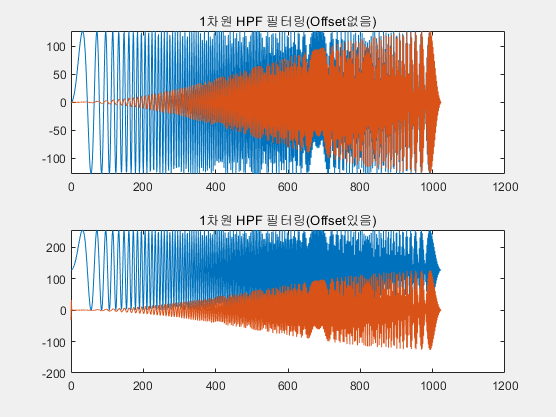
offset을 제거함