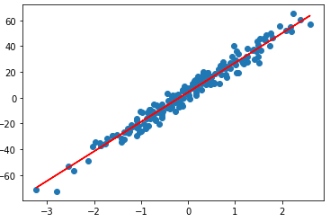
1. 손실 함수
: 학습 과정이 얼마나 잘 되고 있는지 나타내는 지표로서
낮을 수록 성능이 좋다.
손실 함수 결과에 따라 파라미터 조정하며 학습을 진행하고
미분 가능한 함수를 사용하여야 한다.
1-1. 평균절대오차(MAE)
: 오차가 커져도 MAE(손실함수)는 일정하게 증가함
즉, 이상치(Outlier)에 강건한 특성
회귀에 많이 사용됨
1-2. 평균제곱오차(MSE)
: 오차가 커질수록 MSE(손실함수)가 빠르게 증가
정답과 예측값 차이가 클 수록 더 많은 패널티 부여
가장 자주 사용하는 손실함수로서, 회귀(Regression)에 주로 사용
Q. 평균절대오차(Mean Absolute Error, MAE)는 평균제곱오차(Mean Squared Error, MSE)는 서로 어떤 공통점과 차이점이 있나요?
평균제곱오차(MSE) 와 평균절대오차(MAE) 는
둘 다 예측 값과 실제 값 사이의 차이로 오차를 계산하는 방식의 손실함수 이다.
그리고 둘 다 회귀 문제에서 사용된다.
하지만 MAE는 제곱을 사용하지 않으므로 큰 오차에 민감성이 낮다.
즉, 이상치의 영향을 상대적으로 덜 받기 때문에
일반적으로 이상치가 많은 경우에 사용될 수 있다.
반면, MSE는 제곱을 사용하므로 연속적이고 미분 가능한 손실 함수로서
이상치에 큰 영향을 받지만 최적화에 유리하다는 특성이 있다.
따라서 경사 하강법과 같은 최적화 알고리즘에서 더 쉽게 사용가능하다.
문제와 데이터의 특성에 따라 어떤 손실 함수가 적합할지는 생각해 보아야 할 문제이다.
Q. 평균절대오차(Mean Absolute Error, MAE)는 평균제곱오차(Mean Squared Error, MSE)와 비교했을 때 어떻게 이상치에 강건할 수 있나요?
MAE는 각 데이터 포인트의 오차를 절댓값으로 계산하고, 이를 평균한 값입니다.
MSE는 각 데이터 포인트의 오차를 제곱하여 계산하고, 이를 평균한 값입니다.
이상치가 있는 경우, 이상치는 실제 값과 모델의 예측 값 사이에 큰 차이를 나타냅니다. 이러한 이상치는 MSE에 큰 영향을 미칩니다. 제곱 오차는 이상치의 크기에 비례하여 크게 증가하기 때문에 MSE는 이상치에 매우 민감합니다.
즉, MAE는 오차의 크기를 제곱하지 않고 절댓값을 사용하기 때문에
이상치의 크기에 비례하지 않는다고 볼 수 있다.
이상치가 있는 경우에도 오차의 크기를 단순히 더하므로
이상치에 상대적으로 덜 영향을 받고 더 강건한 성질을 가지게 된다.
1-3. 원-핫 인코딩
: 정답 레이블만 1, 나머지는 0
범주형 변수 표현을 할 때 사용
레이블인코딩: 0,1,2, 등으로 표기
Q. 정답 클래스가 [0, 0, 1, 0] 꼴로 주어졌을 때 사용하면 좋은 손실함수는 무엇인가요?
Categorical Cross-Entropy(범주형 교차 엔트로피)는 주로 분류 문제에서 사용되는 손실(오차) 함수 중 하나입니다. 이 함수는 신경망이 예측한 확률 분포와 실제 레이블의 분포 사이의 차이를 측정하여 모델을 학습하는 데 사용됩니다.
분류 문제에서, 주어진 입력에 대해 모델은 여러 클래스 중 하나를 예측합니다. Categorical Cross-Entropy는 다음과 같은 과정으로 동작합니다:
모델이 예측한 확률 분포와 실제 레이블을 표현하는 원-핫 인코딩된 벡터 사이의 차이를 계산합니다.
이 차이를 기반으로 손실을 계산하고, 이 손실을 최소화하도록 모델을 학습시킵니다.
1-4. 교차 엔트로피 오차(CEE)
: softmax 결과와 원-핫 인코딩 사이의 출력 거리를 비교하여 오차 계산
정답은 오차가 0, 틀리면 그 차이가 클수록 오차가 무한히 커짐
이진/다중 분류에 주로 사용
이진 분류 문제에서는 교차 크로스 엔트로피(BCE) 주로 사용
2. 옵티마이저와 지표
Optimizer: 손실 함수를 기반으로 모델을 어떻게 업데이트 시킬지 결정하는 기능
SGD나 ADAM 을 많이 씀
2-1. 경사하강법
Gradient Decent: 미분과 기울기로 동작하며, 스칼라를 벡터로 미분
변화가 있는 지점에 미분값이 존재하며, 미분값이 클수록 변화량이 큼
한 스텝(learning rate)마다의 미분값에 따라 이동하는 방향을 결정하여
f(x)의 값이 변하지 않을때까지 반복한다.
2-2. 블록함수와 비블록함수
Convex Function & Non-Convex Function
: 볼록함수는 어떤 지점에서 시작하더라도 최적값(손실함수 최소로 하는 지점)에 도달 가능
비볼록함수는 시작점의 위치에 따라 다른 최적값에 도달할 수 있음
보통 비볼록함수의 경우가 많음
2-3. 안장점
Saddle Point: 기울기가 0이지만 극값이 되지 않는 점
경사하강법은 안장점에서 벗어나지 못하는 문제가 있음
2-4. 학습률
Learning Rate: 학습률이 너무 크면 발산, 너무 작으면 최저점에 도달하지 못하거나 오랜 시간 소요
2-5. 지표
Metrics: mae, acc(uracy) 를 주로 사용
Q. 경사하강법은 무슨 일을 하나요?
옵티마이저는 손실 함수를 기반으로 모델이 어떻게 업데이트되어야 하는지 결정합니다. Keras에서 여러 옵티마이저를 제공하고, 사용자는 특정 종류의 확률적 경사 하강법을 지정할 수 있습니다.
Q. 왜 경사하강법으로는 안장점(Saddle point)에서 벗어나지 못할까요?
기울기의 반대 방향으로 다음 위치를 이동해야하는데 기울기 값이 0이라 이동하지 못합니다.
Q. 학습률은 어디에 사용되고 잘못 설정한 경우 어떤 문제가 발생할 수 있나요?
경사하강법을 통해 손실함수의 반대 기울기 방향으로 업데이트 할 때 업데이트 되는 크기에 관여하며 잘못 설정한 경우 손실함수의 최저점에 도달하지 못할 수 있습니다.
3. 딥러닝 모델 학습

3-1. 데이터 생성
선형회귀(Linear Regression)를 위한 딥러닝 모델 을 만들어보도록 하겠습니다.
먼저 데이터셋을 make_regression 함수를 이용하여 입력 X와 정답 y로
샘플 갯수(n_samples) 200개,
특징 갯수(n_featrues) 1개,
바이어스(bias)는 5.0,
노이즈(noise)는 5.0,
random_state는 123 으로 하여 랜덤 시드를 지정해줍니다.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_regression
X, y = make_regression(n_samples=200, n_features=1,
bias=5.0, noise=5.0, random_state=123)
y = np.expand_dims(y, axis=1)
plt.scatter(X, y)
plt.show()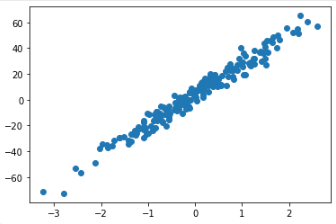
데이터는 학습용 데이터셋(x_train, y_train), 테스트용 데이터셋(x_test, y_test)으로 구분합니다.
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(X, y,
test_size=0.2,
shuffle=True,
random_state=123)
print(x_train.shape, y_train.shape)
print(x_test.shape, y_test.shape)(160, 1) (160, 1)
(40, 1) (40, 1)
3-2. 모델 생성
먼저 딥러닝을 사용하는데 필요한 라이브러리인 Tensorflow와 keras를 임포트합니다.
케라스(Keras)의 모델, 레이어, 옵티마이저, 유틸을 사용할 수 있도록
models, layers, optimizer, utils도 임포트합니다.
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import models, layers, optimizers, utils모델은 간단하게 Sequential()을 이용해 선언하고,Dense 레이어 하나를 추가해줍니다.
레이어의 유닛수는 1개이고, activation은 선형 회귀이니 'linear'로 지정하며,
input_shape은 (1,) 으로 1차원 모양으로 입력 모양을 가집니다.
최종 모델의 구조를 summary() 함수를 통해 확인해봅니다.
model = keras.Sequential()
model.add(layers.Dense(1, activation='linear', input_shape=(1,)))
model.summary()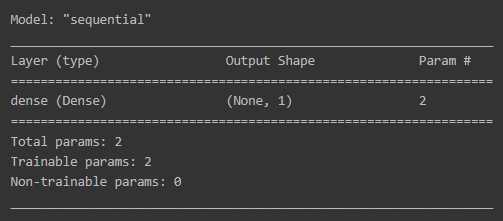
utils.plot_model(model)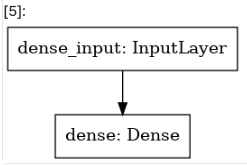
3-3. 모델 학습
딥러닝 모델의 학습 진행 방식을 결정하는 옵티마이저(optimizer)로
SGD(Stochastic Gradient Descent) 를 사용합니다.
compile() 함수를 통해서
손실 함수(loss function), 옵티마이저(optimizer), 지표(metrics)를 지정합니다.
모델의 학습에 필요한 손실 함수로 mse(Mean Square Error)를 사용하고,
옵티마이저는 정의했던 SGD를 사용합니다.
지표로는 mae(Mean Absolute Error)와 mse를 사용합니다.
이제 모델 학습을 진행하기위해 fit() 함수를 호출합니다.
학습을 위해 x_train과 y_train를 지정하고,
학습 반복 횟수(epochs)를 40으로 지정합니다.
optimizer = optimizers.SGD()
model.compile(loss='mse', optimizer=optimizer, metrics=['mae', 'mse'])
history = model.fit(x_train, y_train, epochs=40)모델이 학습하면서 각 epoch 마다 저장한 mae와 mse 지표를 차트를 통해서 확인합니다.
plt.plot(history.history['mae'])
plt.plot(history.history['mse'])
plt.xlabel('Epoch')
plt.legend(['mae', 'mse'])
plt.show();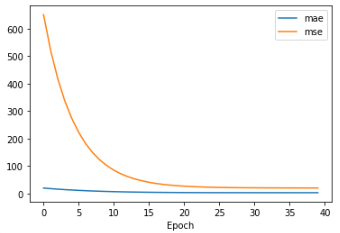
3-4. 모델 평가
이제 모델의 평가를 위해 evaluate() 함수를 이용하여 데이터셋인 x_test, y_test에 대해서 지표인 mae와 mse를 확인합니다.
model.evaluate(x_test, y_test)
3-5. 모델 예측
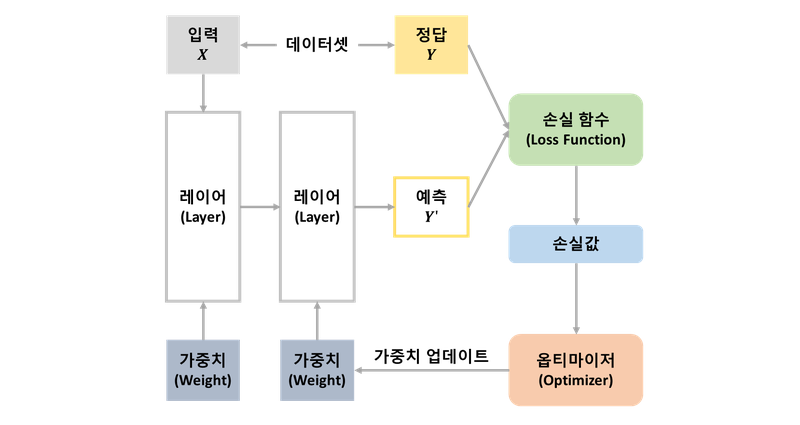
학습된 모델을 통해 입력 데이터 X에 대한 예측값을 predict()를 통해 결과로 받아옵니다.
실제 데이터의 결과값 y와 모델의 예측 결과인 result를 살펴봅니다.
result = model.predict(X)
plt.scatter(X, y)
plt.plot(X, result, 'r')
plt.show()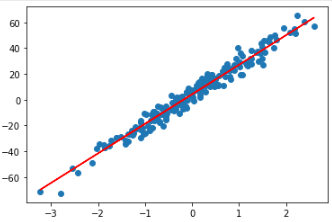
딥러닝 모델에서 사용한 레이어를 layers로 접근하여 살펴볼 수 있습니다.
여기에서는 Dense 레이어 하나만 사용된 것을 알 수 있습니다.
model.layers
모델의 0번째 레이어인 layers[0]를 가져와서 layer.name으로 레이어의 이름을 확인할 수 있습니다.
또한, get_layer() 함수를 통해 같은 이름의 레이어를 얻을 수도 있습니다.
layer = model.layers[0]
print(layer.name)
layer = model.get_layer('dense')
print(layer.name)
레이어에서 사용하는 가중치(weights)와 바이어스(biases)를
get_weights() 함수를 통해서 얻을 수 있습니다.
즉, 레이어에 있는 가중치와 바이어스를 통해 선형 회귀식을 얻을 수 있습니다.
weights, biases = layer.get_weights()
print(weights)
print(biases)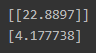
딥러닝 모델에서 학습된 가중치(weights)와 바이어스(biases)를 통해 선형회귀식을 np.array(weights * X + biases) 로 표현할 수 있습니다.
plt.scatter(X, y)
plt.plot(X, np.array(weights * X + biases), 'r')
plt.show()