[머신러닝] 10. 이미지 처리

딥러닝

딥러닝

뇌의 뉴런과 유사한 머신러닝 알고리즘
심층 신경망(DNN, Deep Neural Network)
입력층 – 은닉층 – 출력층이 있음

딥러닝의 학습 과정

순전파: 예측값 계산
손실함수: (예측값과 실제값 사이의) 오차 측정
옵티마이저(최적화): 강사 하강법 등으로 최적의 가중치를 찾아냄
역전파: (각 데이터마다) 가중치 조절

언더피팅과 오버피팅(빈번)

언더피팅은 모델이 학습 데이터를 충분히 학습하지 못한 경우를 의미합니다. 이 경우 모델은 학습 데이터에서의 성능이 낮아지고, 새로운 데이터에 대해서도 성능이 좋지 않을 수 있습니다. 이는 모델이 학습 데이터에서 보지 못한 패턴을 인식하지 못하기 때문입니다.

반면, 오버피팅은 모델이 학습 데이터를 과도하게 학습한 경우를 의미합니다. 이 경우 모델은 학습 데이터에서는 높은 성능을 보이지만, 새로운 데이터에 대해서는 성능이 좋지 않을 수 있습니다. 이는 모델이 학습 데이터에서의 잡음(noise)이나 특이한 패턴까지 학습하기 때문입니다.

언더피팅과 오버피팅 모두 모델의 성능을 저하시키므로, 적절한 모델 복잡도와 학습 데이터의 양과 질을 고려하여 이를 최소화해야 합니다. 이를 위해 교차 검증(cross-validation)이나 정규화(regularization) 등의 방법을 사용할 수 있습니다.

train loss (영상의 파란색 곡선): 학습이 진행될수록 감소 -> train dataset에 맞게 모델이 학습되고 있음

validation loss (영상의 주황색 곡선): 특정 시점 이후로 증가 -> 오버피팅

에폭(Epoch)

데이터 셋을 모두 학습한 상태 (루프 N회)

텐서플로(Tensorflow)

2015년 구글 브레인팀에 의해 공개된 머신러닝을 위한 무료 오픈 소스 라이브러리
고수준 API 지원 (keras)
자동 미분

Sequential 모델

레고블럭처럼 원하는 레이어만 불러들여서 쌓게 되면
하나의 딥러닝 모델을 만들 수 있다.

compile

딥러닝에서의 compile은 모델을 학습(fit)할 준비를 하는 단계입니다. 딥러닝 프레임워크에서 모델을 구성하고 학습 과정을 설정하는 단계 중 하나입니다. 보통은 케라스(Keras), 텐서플로우(TensorFlow) 등의 프레임워크에서 사용되는 용어입니다.

compile 단계에서는 세 가지 주요한 구성 요소를 설정합니다:

Optimizer(옵티마이저): 모델이 손실 함수를 최소화하기 위해 가중치를 업데이트하는 알고리즘입니다. 경사 하강법의 변종으로, Adam, SGD 등의 옵티마이저를 선택할 수 있습니다.

Loss(손실 함수): 모델이 학습하는 동안 사용되는 손실 함수를 지정합니다. 이 손실 함수는 모델의 예측과 실제 값 사이의 차이를 측정하며, 최소화하려는 대상입니다. 분류 문제에서는 'binary_crossentropy'나 'categorical_crossentropy'와 같은 손실 함수를 사용하고, 회귀 문제에서는 'mean_squared_error'를 주로 사용합니다.

Metrics(평가 지표): 모델의 성능을 측정하는 데 사용되는 지표를 선택합니다. 예를 들어, 분류 문제에서는 'accuracy'(정확도), 'precision'(정밀도), 'recall'(재현율) 등이 사용될 수 있습니다.

compile 단계를 통해 설정된 이러한 구성 요소는 모델이 학습을 시작할 때 사용되며, 실제로 모델이 데이터를 통해 학습할 때 이러한 설정에 따라 가중치가 업데이트되고 손실이 계산됩니다.

이미지 분류

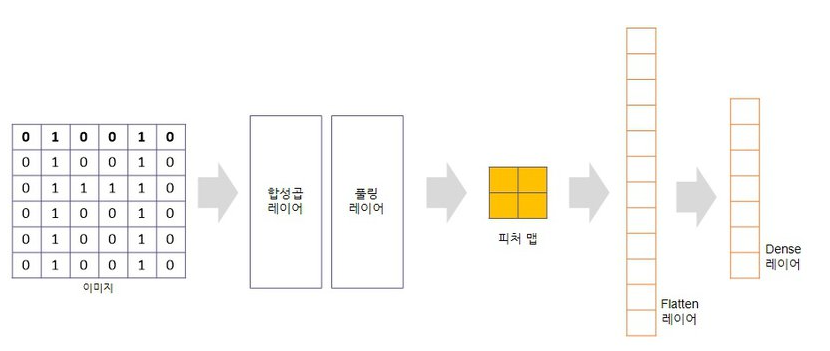
Flatten Layer

keras에서 제공하는 함수인 Flatten을 통해 다차원 배열 공간을 1차원으로 평탄화 해준다.
예 : (영상 설명 참고) 28x28 크기의 데이터를 1차원으로 평탄화 -> 길이가 784인 벡터

Dense Layer

입력과 출력을 모두 연결해 준다. 입력 뉴런이 2개, 출력 뉴런이 4개라고 할때 총 연결선은 2x4개가 된다. 각 연결선은 가중치(연결 강도)를 포함한다.

activation(활성화 함수)

softmax : 확률 값 출력, 가장 높은 확률 값을 가지는 클래스 선택
ReLU : x가 0보다 작으면 0을 출력하고, x가 0보다 크면 x값을 출력한다.

optimizer(최적화 알고리즘)

손실함수(Loss Function)를 최소화 하면서 학습하는 방법
optimizer 자세히 알아보기
Loss Function 자세히 알아보기

1. mnist 데이터

손으로 쓴 숫자, 흑백 , 28x28픽셀

# 라이브러리 불러오기
import tensorflow as tf
import matplotlib.pyplot as plt

# version
tf.__version__

# 데이터셋 불러오기
mnist = tf.keras.datasets.mnist
(X_train, y_train), (X_test, y_test) = mnist.load_data()

# 데이터 크기
X_train.shape, y_train.shape, X_test.shape, y_test.shape

# 데이터 확인
import numpy as np
np.set_printoptions(linewidth=120)
print(X_train[0])

# 데이터 확인(이미지)
plt.imshow(X_train[0])

# label 확인
y_train[0]

# 모델 (sequential 3개를 쌓아서 모델을 만듦)
from tensorflow.keras.layers import Flatten, Dense
from tensorflow.keras.models import Sequential

model = Sequential([
                    Flatten(input_shape=(28, 28)),		# 2 -> 1차원 데이터로 변환
                    Dense(256, activation='relu'),		# 완전연결 레이어 뉴런이 256
                    Dense(10, activation='softmax')		# 합이 1인 확률값으로 나오게 됨, 그 중 가장 큰 값을 선택하게 됨
])


# 모델 요약  (28 * 28 = 784)
model.summary()

# (모델 만든 후) 컴파일 : 3가지를 설정해야 함
model.compile(optimizer='adam',
              loss='sparse_categorical_crossentropy',		# loss는 분류
              metrics=['accuracy'])

# 학습
history = model.fit(X_train, y_train, epochs=5) 


# 결과를 보면 60000 데이터 중에 1875개만 학습되는 것을 볼 수 있음
# 딥러닝의 기본 배치 사이즈는 32, 따라서 60000//32 = 1875
# 에폭 진행될수록 loss는 떨어지고, accuracy는 높아지는 것을 확인할 수 있음

# 학습 정확도 (epoch에 따른 accuracy 변화)
plt.plot(history.history['accuracy'], label='acc')
plt.xlabel('epochs')
plt.ylabel('accuracy')
plt.legend()

# loss
plt.plot(history.history['loss'], label='loss')
plt.xlabel('epochs')
plt.ylabel('loss')
plt.legend()

fashion-mnist 데이터

10개 클래스, 그레이, 28x28픽셀

# 라이브러리 불러오기
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

# 데이터 불러오기 
mnist = tf.keras.datasets.fashion_mnist
(X_train, y_train), (X_test, y_test) = mnist.load_data()

# 정규화(0~1 사이)
X_train, X_test = X_train / 255.0, X_test / 255.0


# 데이터 확인(이미지) 
plt.imshow(X_train[0])
y_train[0]


# 위 결과가 숫자로 나왔기 때문에 label 확인
classes = [
    "T-shirt/top", "Trouser", "Pullover", "Dress", "Coat", 
    "Sandal", "Shirt", "Sneaker", "Bag", "Ankle boot",
]

print(classes[y_train[0]])


# 데이터 확인(이미지, 레이블)
print(classes[y_train[1]])
plt.imshow(X_train[1])


# 모델 (Dense는 완전연결(선이 뉴런), Dropout은 랜덤생략하여 과적합 방지함) 
from tensorflow.keras.layers import Flatten, Dense, Dropout
from tensorflow.keras.models import Sequential

model = Sequential([
                    Flatten(input_shape=(28, 28)),
                    Dense(128, activation='relu'),
                    Dropout(0.2),    # Dense 레이어에서 연결의 20% 생략
                    Dense(10, activation='softmax')
])


# 컴파일 : 3가지만 하면 됨
model.compile(optimizer='adam',
              loss='sparse_categorical_crossentropy',  # 숫자가 아닌 원핫인코딩의 경우에는 sparse 없이 적어주기
              metrics=['accuracy'])

# 학습

# 방법1 : 데이터의 20%를 자동으로 validation data로 지정
# history = model.fit(X_train, y_train, validation_split=0.2, epochs=5)

# 방법2 : 특정 dataset을 validation data로 사용
history = model.fit(X_train, y_train, validation_data=(X_test, y_test), epochs=10)


# 학습 정확도
plt.plot(history.history['accuracy'], label='acc')
plt.plot(history.history['val_accuracy'], label='val')
plt.xlabel('epochs')
plt.ylabel('accuracy')
plt.legend()

plt.plot(history.history['loss'], label='train')
plt.plot(history.history['val_loss'], label='val')
plt.xlabel('epochs')
plt.ylabel('loss')
plt.legend()


# 예측
pred = model.predict(X_test)
pred[1]
np.argmax(pred[1])				# 가장 높은/큰 값 찾기

# 예측한 label 
classes[np.argmax(pred[1])]

# 실제 label
classes[y_test[1]]

# 이미지 확인
plt.imshow(X_test[1])

CNN을 활용한 이미지 분류

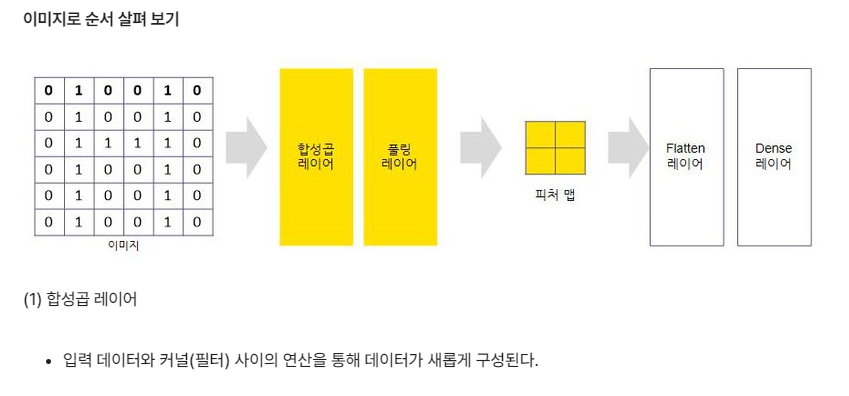
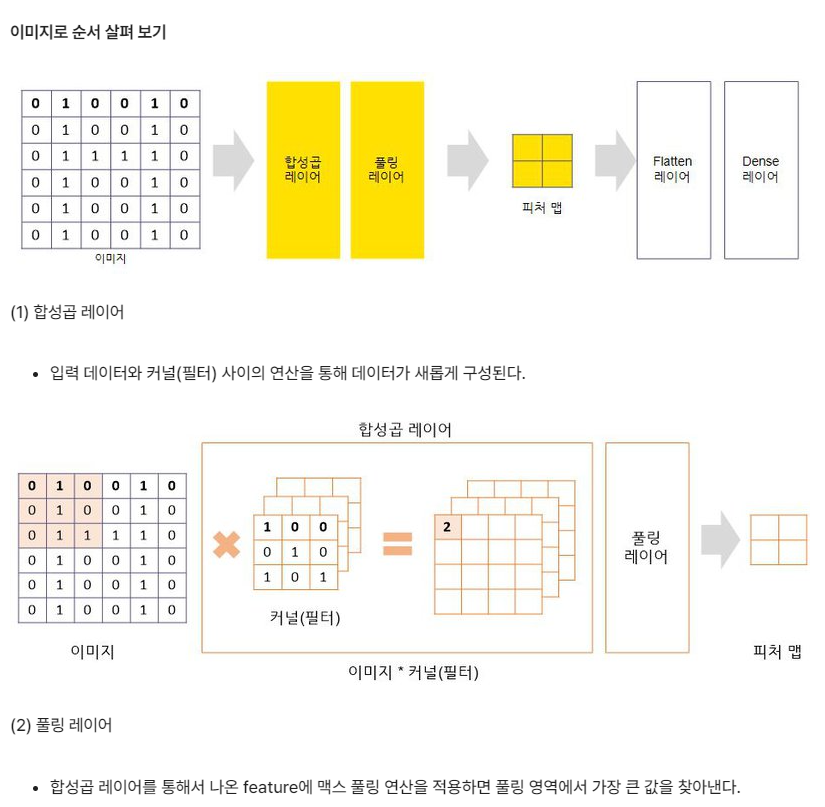
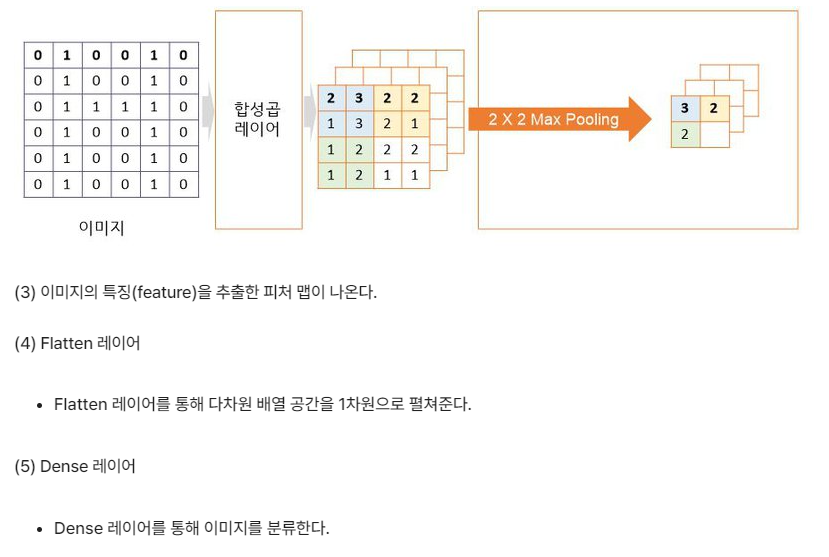
CNN(합성곱 신경망 )

시각적 영상을 분석하는 데 사용되는 다층의 피드-포워드적인 인공신경망의 한 종류
합성곱층(Convolution layer)과 풀링층(Pooling layer)으로 구성

# 라이브러리 불러오기
import tensorflow as tf
import matplotlib.pyplot as plt
from tensorflow.keras.layers import Flatten, Dense, Dropout, Conv2D, MaxPooling2D
from tensorflow.keras.models import Sequential

# 데이터 불러오기 
mnist = tf.keras.datasets.fashion_mnist
(X_train, y_train), (X_test, y_test) = mnist.load_data()

# shape 변경
X_train = X_train.reshape((60000, 28, 28, 1))
X_test = X_test.reshape((10000, 28, 28, 1))

# 정규화(0~1 사이)
X_train, X_test = X_train / 255.0, X_test / 255.0

# 모델
model = Sequential([
                    Conv2D(32, (3, 3), activation='relu', input_shape=(28, 28, 1)),
                    MaxPooling2D((2, 2)),
                    Conv2D(64, (3, 3), activation='relu'),
                    MaxPooling2D((2, 2)),
                    Conv2D(64, (3, 3), activation='relu'),
                    MaxPooling2D((2, 2)),
                    Flatten(),
                    Dense(64, activation='relu'),
                    Dense(10, activation='softmax')
])

# 컴파일
model.compile(optimizer='adam',
              loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])
              
model.summary()


# 학습
# (CPU 환경에서 10분 이상 소요될 수 있습니다. 시간이 너무 오래 걸리는 경우 epoch 수를 줄여보세요)

history = model.fit(X_train, y_train, validation_data=(X_test, y_test), epochs=10)

              
# 학습 정확도
plt.plot(history.history['accuracy'], label='acc')
plt.plot(history.history['val_accuracy'], label='val')
plt.xlabel('epochs')
plt.ylabel('accuracy')
plt.legend()

# loss
plt.plot(history.history['loss'], label='train')
plt.plot(history.history['val_loss'], label='val')
plt.xlabel('epochs')
plt.ylabel('loss')
plt.legend()