로지스틱 회귀 (LogisticRegression)

ppippi·2023년 7월 12일

Machine Learning(ML) 기초 및 응용

목록 보기

11/11

이전 포스팅에서 경사하강법을 설명한 이유는 로지스틱 회귀 (LogisticRegression)에서 경사하강법을 사용하기 때문이다.

로지스틱 회귀 (LogisticRegression)

로지스틱 회귀 (LogisticRegression) = 시그모이드 함수(sigmoid function)

선형회귀는 알고리즘을 이용한 이진 분류 모델이다.
이 모델은 주어진 데이터를 기반으로 샘플이 특정 클래스에 속할 확률을 추정하는 것이 목표이다.
**확률 추정**
로지스틱 회귀에서는 입력된 특성(Feature)에 가중치 합을 계산한 값(선형 회귀)을 로지스틱 함수에 적용하여 확률을 계산한다.
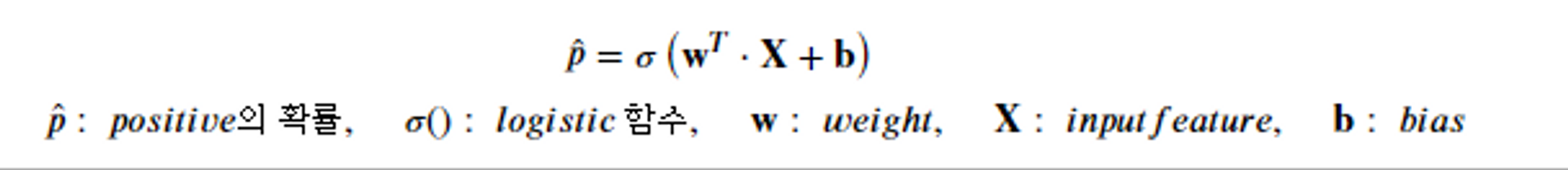
**로지스틱 함수**

로지스틱 함수는 0과 1 사이의 실수를 반환하는 시그모이드 함수로 알려져 있다.

0과 1사이의 실수를 반환
S 자 형태의 결과를 내는 시그모이드 함수(sigmoid function)는 입력값을 0과 1 사이로 압축하여 확률로 해석할 수 있게 한다.

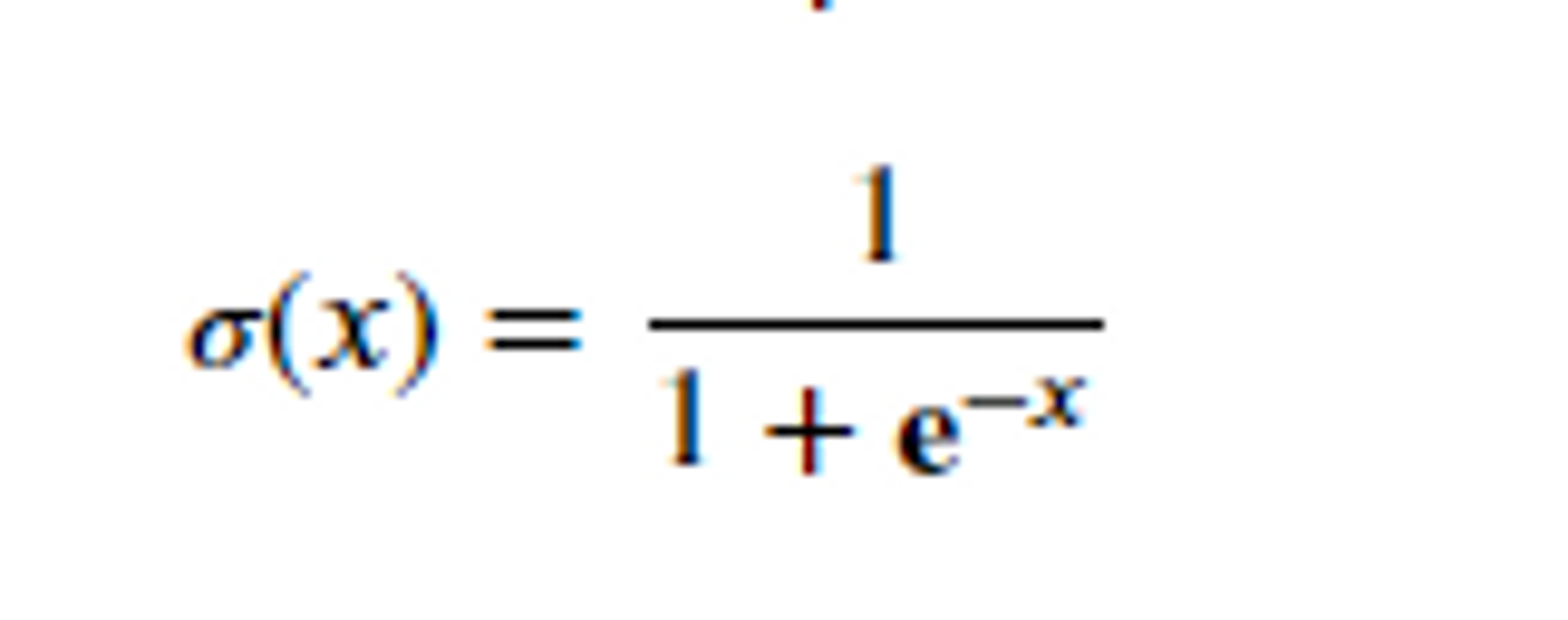
샘플 x가 양성에 속할 확률

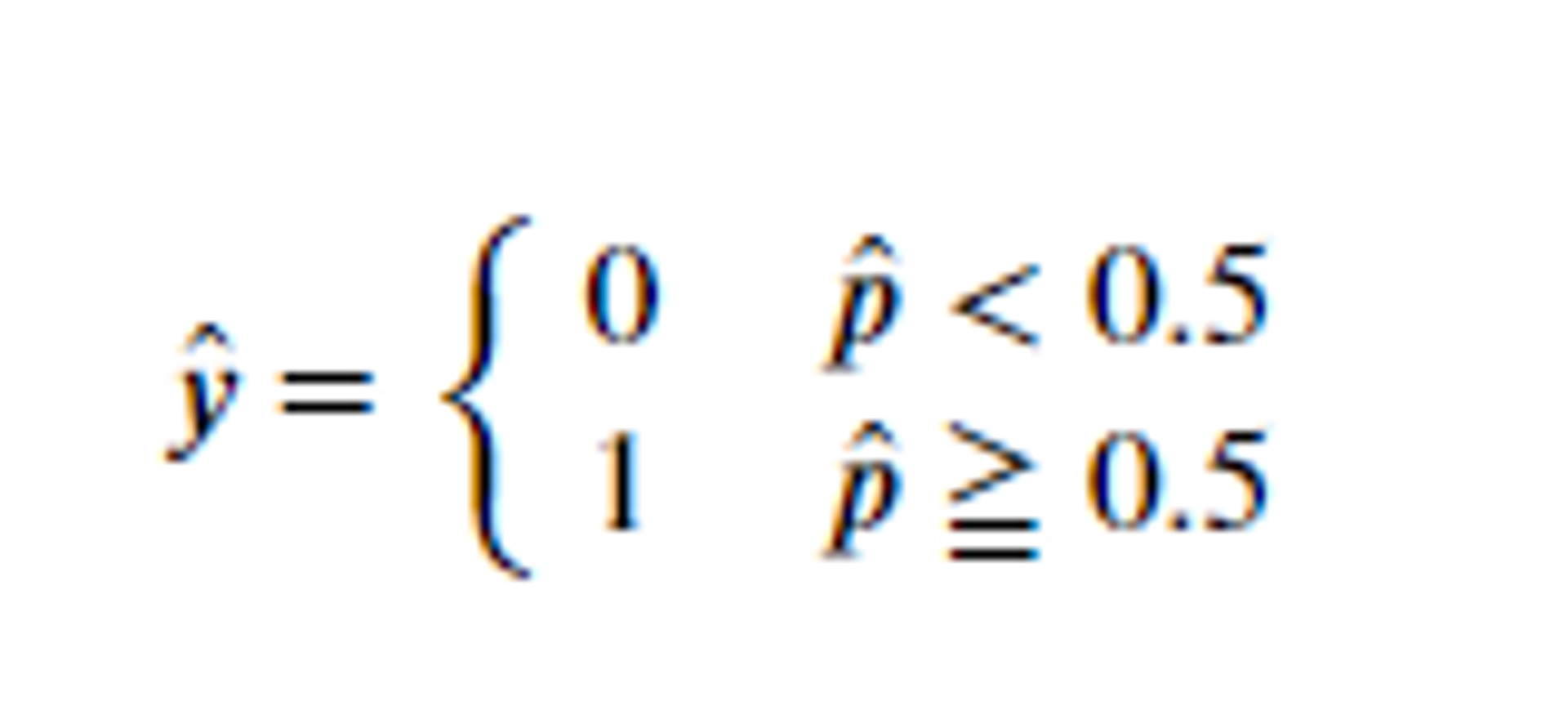
<예제를 통해 살펴보자>

import matplotlib.pyplot as plt
import numpy as np

def logistic_func(X):
    return 1 / (1 + np.exp(-X))

X = np.linspace(-10, 10, 1000)  # x 값을 생성합니다
y = logistic_func(X)

print("y의 최소값:", np.min(y))
print("y의 최대값:", np.max(y))

plt.figure(figsize=(13, 6))
plt.plot(X, y, color='b', linewidth=2)
plt.axhline(y=0.5, color='r', linestyle=':')  # 양성과 음성의 기준선인 0.5를 빨간색 점선으로 표시합니다
plt.ylim(-0.15, 1.15)
plt.yticks(np.arange(-0.1, 1.2, 0.1))

# 축 조작
ax = plt.gca()
ax.spines['left'].set_position("center")
ax.spines['bottom'].set_position(("data", 0.0))
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)

plt.show()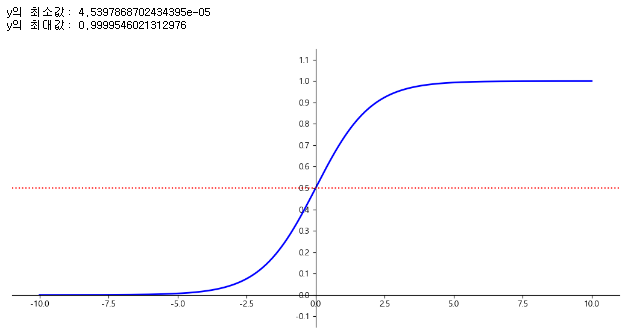

LogisticRegression의 손실 함수(Loss Function)

그냥 분류에서 사용하는 손실함수라고 생각하면된다.
다시한번 설명하자면
손실 함수는 모델이 예측한 정답의 확률에 대해 log를 취해 손실 값을 구하는 방식으로, 일반적인 분류에서 사용되는 손실 함수이다.
로지스틱 회귀에서는 샘플이 양성 클래스에 속할 확률을 계산하며, 손실 함수를 사용하여 학습한다.

로지스틱 회귀에서 사용하는 손실함수
- Log loss
  - 로그 손실은 이진 분류에서 사용
  - 모델이 예측한 정답의 확률에 대해 log를 취해 손실값(오차)을 구한다.
    
    why?
    
    단순히 뺐더니 오차 범위가 작게 나오더라
    그래서 log를 사용해서 정답에 대해 추정한 확률을 넣어 오차범위를 크게 해주려고이다.
  - 수식화
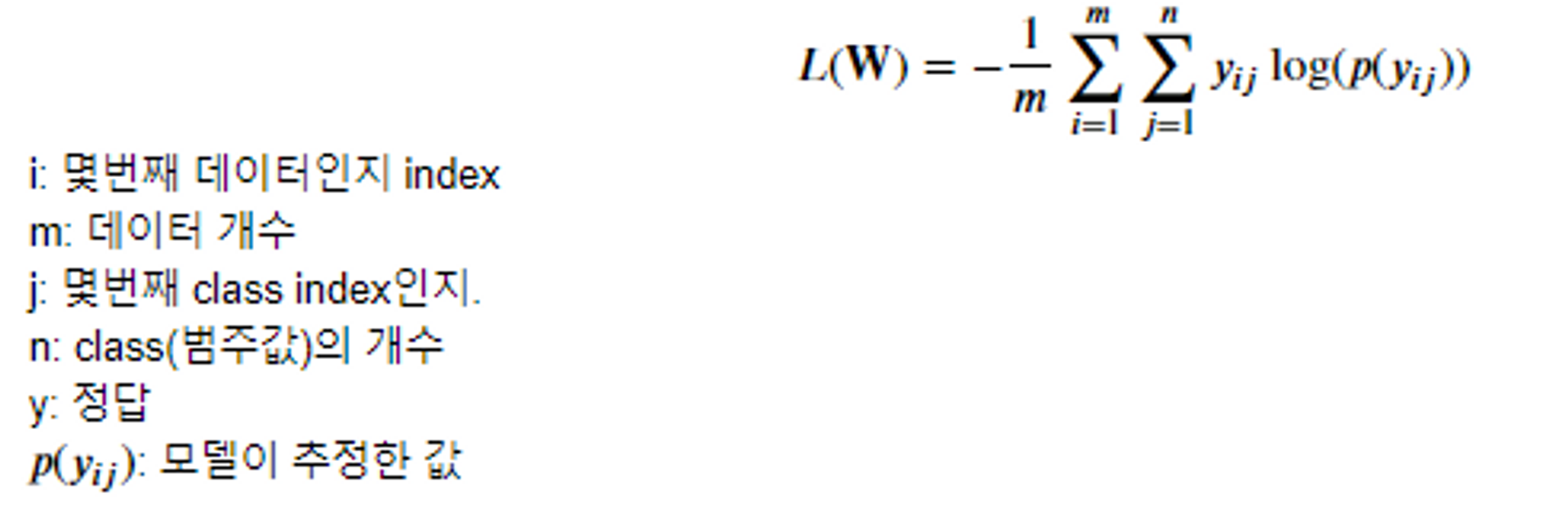
- Cross Entropy
  - 다중 분류에서는 Cross Entropy 손실을 사용
  - 다중분류에 대한 log loss 공식

0log(0.1) + 1log(0.7) + 0log(0.1) + 0log(0.1) => log(0.7)

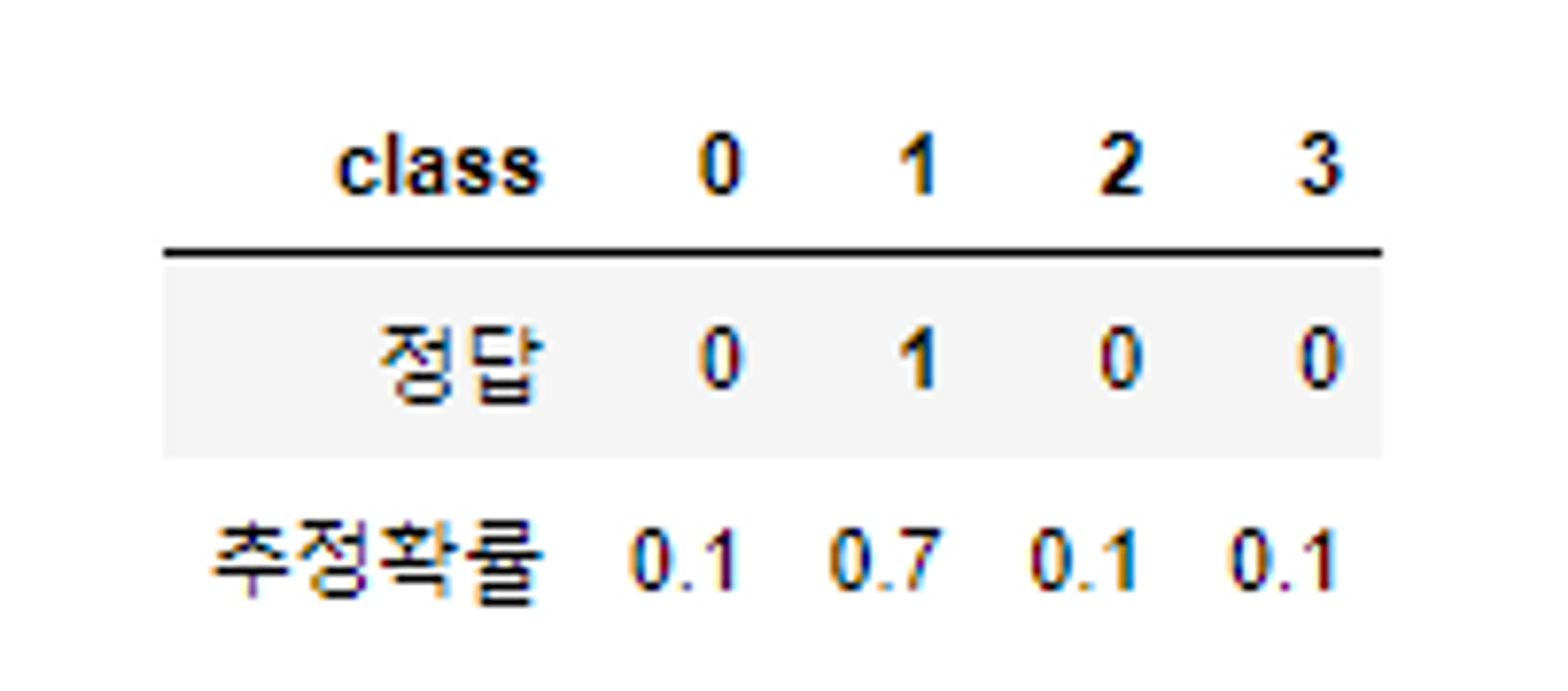
다중분류에 대해서는 cross 방식을 사용하겠다.
- Binary Cross Entropy
- 이진분류 추론 결과에 대한 cross entropy 계산
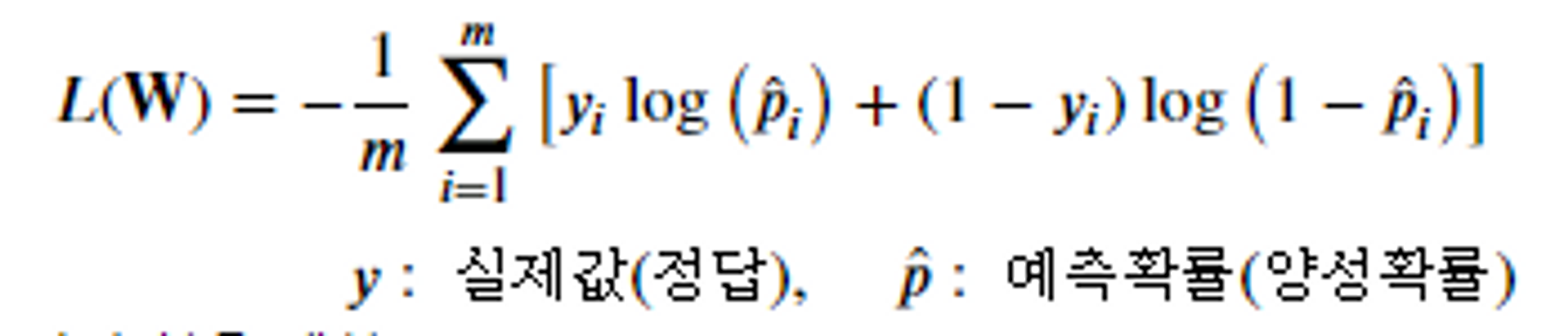
- y(실제값) 이 1인 경우 $y_{i}\log{\left(\hat{p}_i\right)}$ 이 손실을 계산
- y가 0인 경우 $\left( 1 - y_i \right) \log{\left( 1 - \hat{p}_i \right)}$ 이 손실을 계산

LogisticRegression 주요 하이퍼파라미터
- penalty: 과적합을 줄이기 위한 규제방식으로 규제 방식을 결정
  - 'l1', 'l2'(기본값), 'elasticnet', 'none' ⇒ elasticnet: 'l1', 'l2'합친 것.
  - • C: 규제강도(기본값 1) - 작을 수록 규제가 강하다(단순). - 역순이다. => 규제 강도를 조절
  - max_iter(기본값 100) : 경사하강법 반복횟수 설정

<예제로 살펴보자>

import numpy as np
import matplotlib.pyplot as plt

print(1.0 - 0.00000000000000000000000001)

# 모델이 추정한 정답 확률
print("완벽 정답:", np.log(1.0))
print("완벽 틀린:", -np.log(0.00000000000000000000000001))

X = np.linspace(0.0000000000000001, 1, 1000)
y = -np.log(X)

plt.plot(X, y)
plt.grid(True)
plt.show()

print("0.51의 로그 손실:", -np.log(0.51))
print("0.7의 로그 손실:", -np.log(0.7))
print("0.99의 로그 손실:", -np.log(0.99))

print("0.49의 로그 손실:", -np.log(0.49))
print("0.00000000000000000000000000001의 로그 손실:", -np.log(0.00000000000000000000000000001))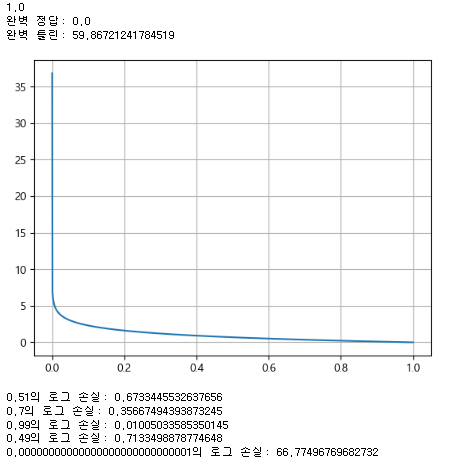

<마무리>

로지스틱 회귀는 이러한 손실 함수를 최소화하는 방향으로 모델 파라미터를 업데이트하여 학습합니다. 이를 통해 입력 데이터에 대한 예측 성능을 향상시킬 수 있습니다.

최적화

최적화
모델이 예측한 결과와 실제 값 사이의 차이인 오차를 가장 작게 만드는 파라미터를 찾는 과정
손실 함수, 비용 함수, 목적 함수, 오차 함수
- 손실 함수, 비용 함수, 목적 함수, 오차 함수는 모델의 예측 값과 실제 값의 차이를 계산하는 함수이다.
최적화의 목적
- 손실 함수의 반환 값을 최소화하는 파라미터를 찾는 것이다.
LogisticRegression에서는 분류 문제이므로 크로스 엔트로피나 로그 손실 함수를 손실 함수로 사용한다.
LogisticRegression의 최적화 과정에서는 경사 하강법을 사용하여 최소 값을 찾는다.
경사 하강법은 손실 함수의 기울기를 계산하여 기울기가 0이 될 때까지 파라미터를 업데이트합니다.
로지스틱 회귀의 주요 하이퍼파라미터
- penalty: 과적합을 줄이기 위한 규제 방식을 선택합니다. 'l1', 'l2', 'elasticnet', 'none' 등이 있습니다.
- C: 규제 강도를 조절하는 매개변수입니다. 작을 수록 규제가 강합니다.
- max_iter: 경사 하강법의 반복 횟수를 설정합니다.

<예제를 살펴보자>

from dataset import get_breast_cancer_dataset
from sklearn.linear_model import LogisticRegression
from metrics import print_metrics_classification
from sklearn.model_selection import GridSearchCV
import pandas as pd

# 데이터셋 로드
(X_train, X_test, y_train, y_test), feature_names = get_breast_cancer_dataset(scaling=True)

# LogisticRegression 모델 초기화 및 학습
lr = LogisticRegression(random_state=0)
lr.fit(X_train, y_train)

# 학습된 모델의 계수와 절편 출력
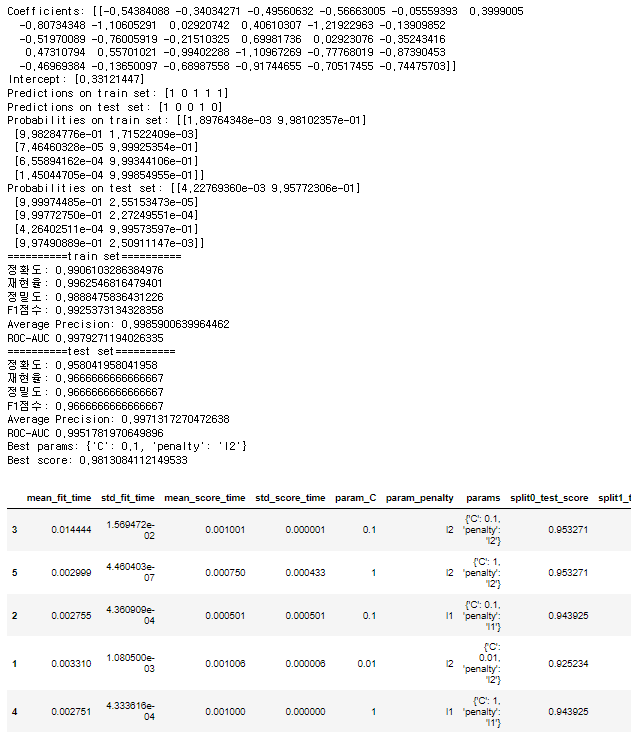
print("Coefficients:", lr.coef_)
print("Intercept:", lr.intercept_)

# 학습 데이터와 테스트 데이터에 대한 예측 수행
pred_train = lr.predict(X_train)
pred_test = lr.predict(X_test)
print("Predictions on train set:", pred_train[:5])
print("Predictions on test set:", pred_test[:5])

# 학습 데이터와 테스트 데이터에 대한 예측 확률 계산
proba_train = lr.predict_proba(X_train)
proba_test = lr.predict_proba(X_test)
print("Probabilities on train set:", proba_train[:5])
print("Probabilities on test set:", proba_test[:5])

# 학습 데이터와 테스트 데이터에 대한 성능 메트릭 출력
print_metrics_classification(y_train, pred_train, proba_train[:, 1], "train set")
print_metrics_classification(y_test, pred_test, proba_test[:, 1], "test set")

# 그리드 서치를 사용한 최적의 하이퍼파라미터 탐색
params = {
    'penalty': ['l1', 'l2'],  # L1: Lasso, L2: Ridge, None: Linear Regression
    'C': [0.01, 0.1, 1, 5, 10],  # 작을수록 강한 규제(overfitting 방지)
}
# solver: 최적화 알고리즘 (liblinear로 설정)
gs = GridSearchCV(LogisticRegression(random_state=0, solver='liblinear'),
                  params,
                  scoring='accuracy',
                  cv=4,
                  n_jobs=-1)
gs.fit(X_train, y_train)

# 최적의 하이퍼파라미터와 최고 점수 출력
print("Best params:", gs.best_params_)
print("Best score:", gs.best_score_)

# 그리드 서치 결과를 데이터프레임으로 변환하여 상위 5개 출력
result = pd.DataFrame(gs.cv_results_)
result.sort_values('rank_test_score').head()

ppippi

이전 포스트

로지스틱 회귀 (LogisticRegression)

Machine Learning(ML) 기초 및 응용

로지스틱 회귀 (LogisticRegression)

LogisticRegression의 손실 함수(Loss Function)

최적화

최적화-경사하강법

0개의 댓글