최적화 - 경사하강법

• 선형회귀 알고리즘을 이용한 이진 분류 모델이다,

• 최적화 (Optimize)
  • 모델의 성능을 높여주는 것. → 그러기 위해서는 파라미터를 찾아야한다. 즉, 모델이 예측한 결과와 정답간의 차이(오차)를 가장 적게 만드는 Parameter를 찾는 과정을 최적화라고 한다.
  • 함수 f(w) 의 값을 최소화(또는 최대화) 하는 변수 w(파라미터)를 찾는 것.
    
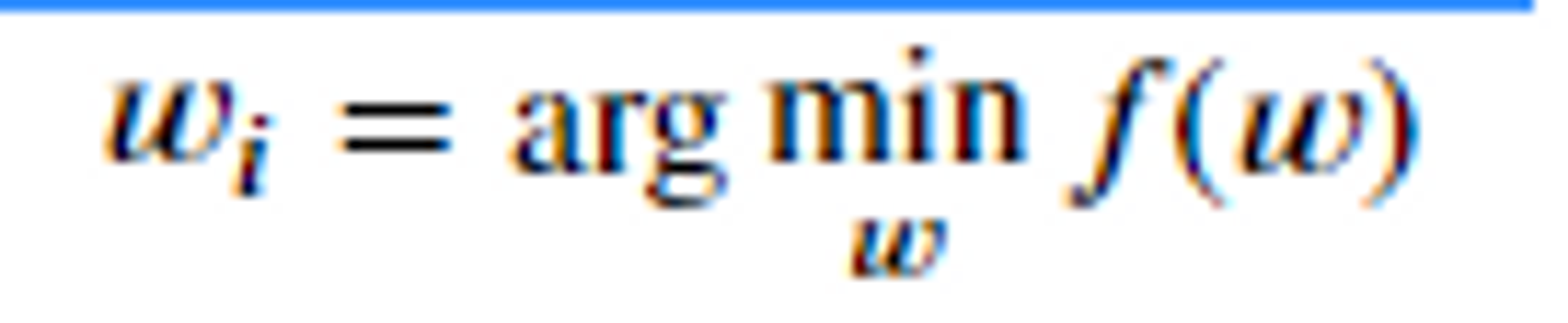
    ⇒ arg의 값(매개변수)을 w로 전달했을때 가장 작은 최소값이 나오는 것을 찾는 것이다.
    ⇒ f(w): 손실함수
    ⇒ 손실함수에 어떤 w(파라미터)를 전달 했을때 손실이 가장 적을까를 찾는 것을 최적화라고 한다.

---

손실함수(Loss Function), 비용함수(Cost Function), 목적함수(Object Function), 오차함수(Error Function)

• 다 같은 함수인데 어떤 관점에서 보는지에 따라 부르는게 다를 뿐 모두 모델의 예측한 값과 실제값 사이에 얼마나 차이가 나는지 오차를 계산하는 함수이다.

• 학습할 때 사용(모델이 파라미터를 찾을 때)

• 평가함수(최종적으로 모델의 성능이 어떤지 판정하는 함수) 와 손실함수(학습하는 도중 얼마나 오차가 났는지 계산하는 함수)는 다르다.

• 해결하려는 문제에 맞춰 Loss 함수를 기반으로 정의한다.

  • Classification(분류)의 경우 cross entropy를 사용
  • Regression(회귀)의 경우 MSE(Mean Squared Error)를 사용

• 최적화 문제를 해결하는 방법(fit할때 해줌)

• Loss 함수 최적화 함수를 찾기

  • Loss를 최소화하는 weight들을 찾는 함수(공식)을 찾는다.
  • Feature와 sample 수가 많아 질 수록 학습하는데 계산량이 많아진다. → 자원도 많이쓰고, 시간도 오래걸린다.
  • 최적화 함수가 없는 Loss함수도 있다.

• 경사하강법 (Gradient Descent)

• 최적화는 Loss를 줄이는 것인데 loss함수는 한번에 loss를 줄이는 것인데 경사하강법은 하나씩 줄여가면서 loss를 줄여가는 것이다. → 즉,값을 조금씩 조금씩 조정해나가면서 최소값을 찾는다는 것이다.

딥러닝 모델들에는 최적화방법이 없어 딥러닝 모델들은 경사하강법을 사용한다.

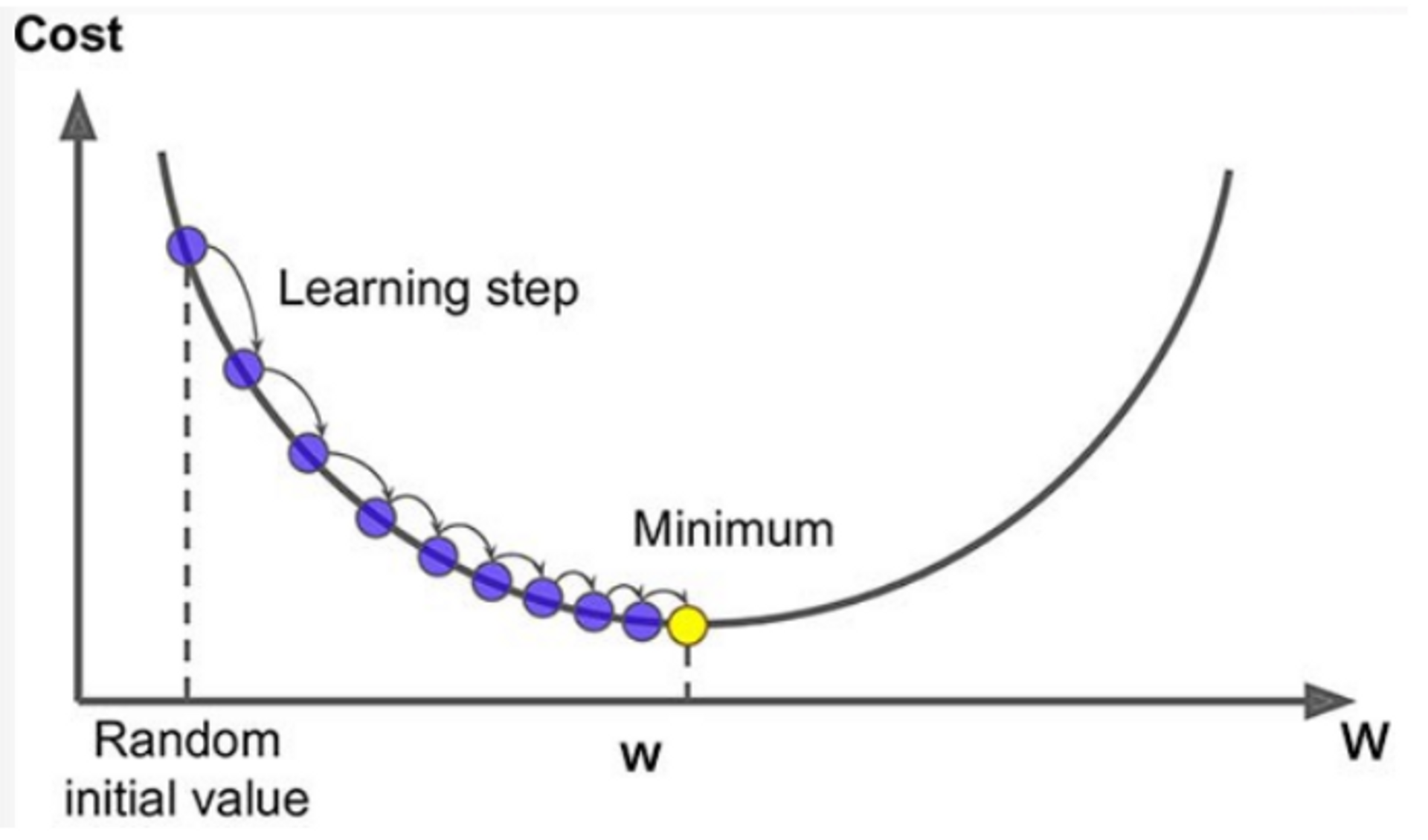
• w(파라미터)에 따라서 오차(cost)는 계속 바뀌는 것이라는 것을 알 수 있다.
• 우리가 찾는 것은 노란색 즉, Minimum이다.
• 오차가 작아지는 방향을 찾아야한다. 초기 파라미터를 잡고 초기w(파라미터)보다 작은 값을 넣어보거나 큰값을 넣어보면서 오차가 작아지는 방향을 찾는다.
• 파라미터 벡터 𝑊에 대해 손실함수의 현재 gradient(경사,기울기)를 계산한다.
  • gradient가 감소하는 방향으로 벡터𝑊를 조정한다.
  • gradient가 0이 될때 까지 반복한다.

즉

• 손실함수를 최소화하는 파라미터를 찾기위해 반복해서 조정해 나간다.
  이때
  • gradient(기울기)가 양수이면 loss와 weight가 비례관계란 의미이므로 loss를 더 작게 하려면 weight가 작아져야 한다. ( / )
  • gradient가 음수이면 loss와 weight가 반비례관계란 의미이므로 loss를 더 작게 하려면 weight가 커져야 한다. ( \ )

• 다양한 종류의 문제에서 최적의 해법을 찾을 수 있는 일반적인 최적화 알고리즘
• 최적화에서는 변화율을 알아야하므로 미분을 사용할 수 밖에없다.
• why? 미분을 이용하면 함수의 변화율을 구할 수 있으며, 이는 함수가 어떻게 변하는지, 어느 지점에서 가장 급격하게 증가하거나 감소하는지 등을 알 수 있게 해주기 때문이다.
  
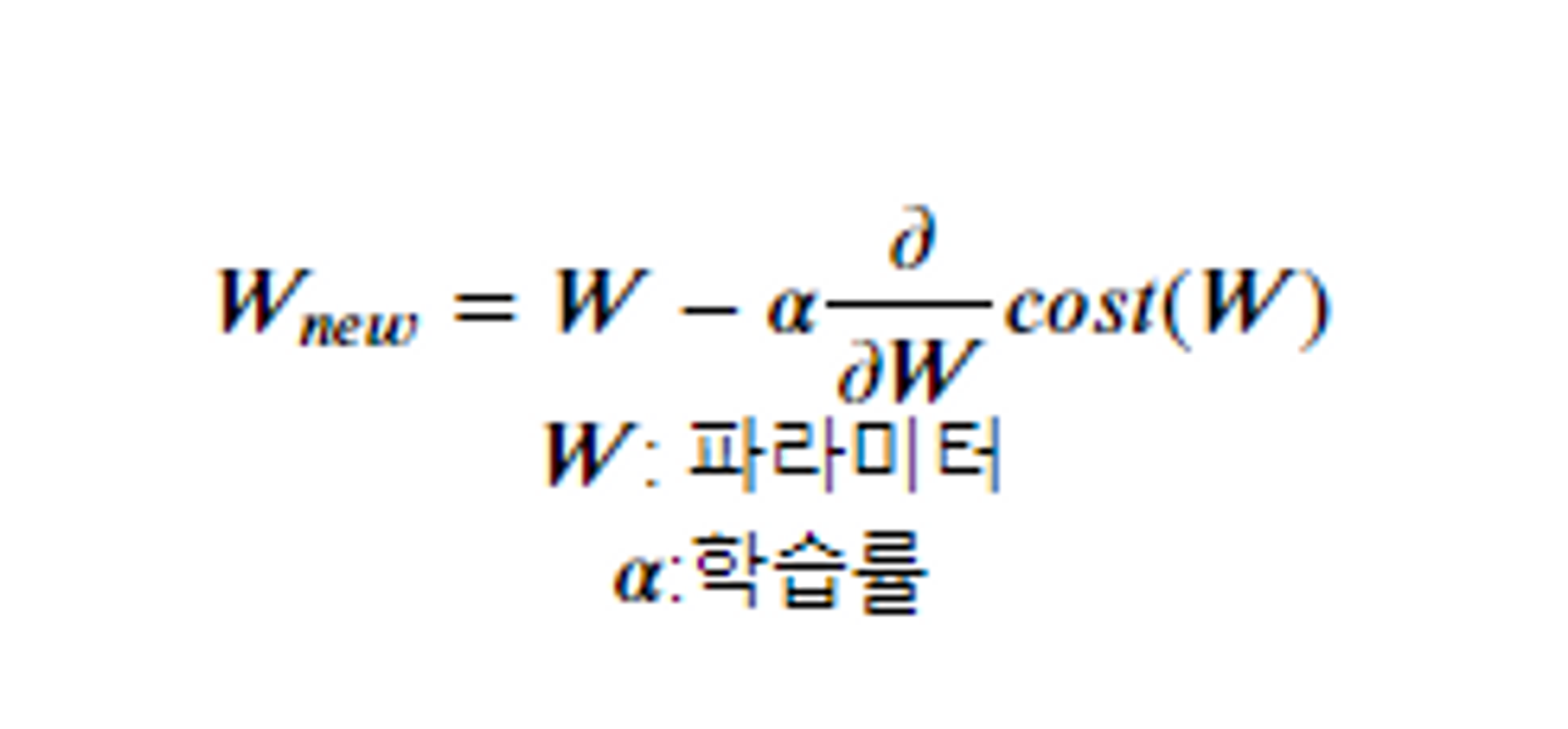
• 현재w값 - a*미분한값
• 미분한 값: 방향을 잡고 최소의 w값 찾기
• a: 학습률 우리가지정해줘야한다. 미분값을 그대로 사용하지 않고 좀 조정해서 사용한다. 기울기에 따라 이동할 step의 크기를 지정해준다.
  • 학습률을 너무 작게 잡으면 최소값에 수렴하기 위해 많은 반복을 진행해야해 시간이 오래걸린다.
  • 학습률을 너무 크게 잡으면 왔다 갔다 하다가 오히려 더 큰 값으로 발산하여 최소값에 수렴하지 못하게 된다.

⇒ 최적의 w가 된것은 기울기가 0이 된 것으로 알 수 있다.

<예제로 확인해 보자>

import numpy as np

def loss(weight):
    return (weight - 1) ** 2 + 2

def derived_loss(weight):
    return 2 * (weight - 1)

np.random.seed(0)

learning_rate = 0.4
max_iter = 100
weight = np.random.randint(-2, 3)
weight_list = [weight]
iter_cnt = 0

while True:
    if derived_loss(weight) == 0 or iter_cnt == max_iter:
        break
    weight = weight - learning_rate * derived_loss(weight)
    weight_list.append(weight)
    iter_cnt += 1

print("Iteration Count:", iter_cnt)
print("Final Weight:", weight)
print("Loss at Final Weight:", loss(weight))
print("Weight History:", weight_list)

=> 초기 파라미터 weight를 랜덤하게 설정하고, 주어진 손실 함수 loss와 그에 해당하는 미분 함수 derived_loss를 사용하여 경사하강법을 수행합니다. 최대 반복 횟수 max_iter와 학습률 learning_rate도 설정합니다.

=> 새로운 weight를 계산하고 업데이트하는 과정을 반복 (반복은 다음 조건 중 하나를 만족할 때까지 수행)
=> 미분값이 0이 되는 경우 또는 최대 반복 횟수에 도달한 경우 반복이 종료된다.