DNN (Deep Neural Network)
-
신경망 구성요소
- 노드/뉴런은 유닛이라고도 할 수 있다.
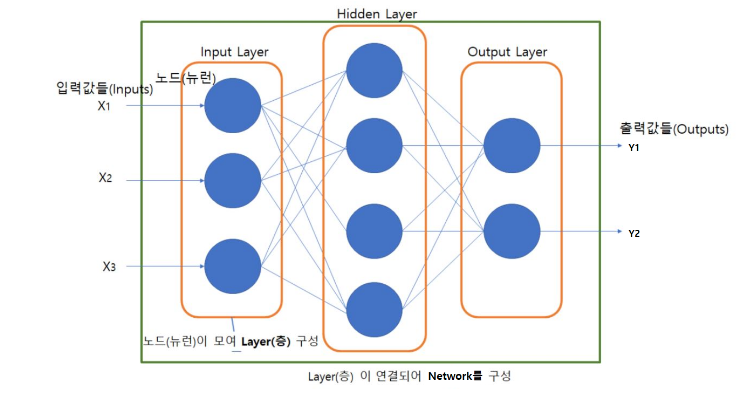
- 노드/뉴런은 유닛이라고도 할 수 있다.
-
활성 함수 (Activation Function)
-
활성화 함수(Activation function)은 인공 신경망에서 뉴런의 출력을 결정하는 함수이다.
-
신경망의 각 층에서 입력 값을 받아 출력 값을 계산할 때 활성화 함수를 적용하여 비선형성을 도입하고 다양한 형태의 함수 근사를 가능하게 한다.
-
활성함수(Activation Function)의 종류
- Sigmoid (logistic function)
수식: 𝜎(𝑥) = 1 / (1 + 𝑒^(-𝑥))
입력 범위: 0과 1 사이로 제한
=> Binary classification(이진 분류)를 위한 네트워크의 Output layer(출력층)의 활성함수로 사용 - Hyperbolic tangent function
수식: 𝑡𝑎𝑛ℎ(𝑥) = (𝑒^𝑥 - 𝑒^(-𝑥)) / (𝑒^𝑥 + 𝑒^(-𝑥))
출력 범위: -1과 1 사이
=> Output이 0을 중심으로 분포하므로 sigmoid보다 학습에 효율적 - ReLU(Rectified Linear Unit)
수식: 𝑅𝑒𝐿𝑈(𝑥) = 𝑚𝑎𝑥(0, 𝑥)
=> 입력이 0보다 작을 때는 0을 출력하고, 0보다 큰 값은 그대로 출력
=> 0이하의 값(z <= 0)들에 대해 뉴런이 죽는 단점이 있다. (Dying ReLU)
[Dying ReLU 문제점 보안]
=Leaky ReLU=
수식: 𝐿𝑒𝑎𝑘𝑦𝑅𝑒𝐿𝑈(𝑥)=𝑚𝑎𝑥(𝛼𝑥,𝑥)
𝛼(alpha)의 범위: 0< 𝛼 < 1
=> 음수 z를 0으로 반환하지 않고 alpah (0 ~ 1 사이 실수)를 곱해 반환- Softmax function
수식: 𝑆𝑜𝑓𝑡𝑚𝑎𝑥(𝑥𝑖) = 𝑒^(𝑥𝑖) / (∑𝑒^(𝑥𝑗)), 𝑖 = 1, 2, ..., 𝑛
=> Multi-class classification(다중 분류)를 위한 네트워크의 Output layer(출력층)의 활성함수로 주로 사용
- Sigmoid (logistic function)
-
위의 활성함수 중 알맞은 활성함수를 선택 후 만약 입력층이 1개 이고 히든층이 3개일 경우 3번의 활성함수를 하게되고 3개의 확률의 총합은 1이 된다.
<코드로 살펴보자>
# 데이터 생성
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(0)
def func(x):
return 3*x**2 + 2 + np.random.rand(*x.shape)*3
# (개수, 1) # randn(): 평균-0, 표준편차-1 (표준정규분포)를 따르는 난수 생성.
X = np.random.randn(100, 1) # (개수,1(Feature개수))
y = func(X)
plt.scatter(X, y)
plt.show()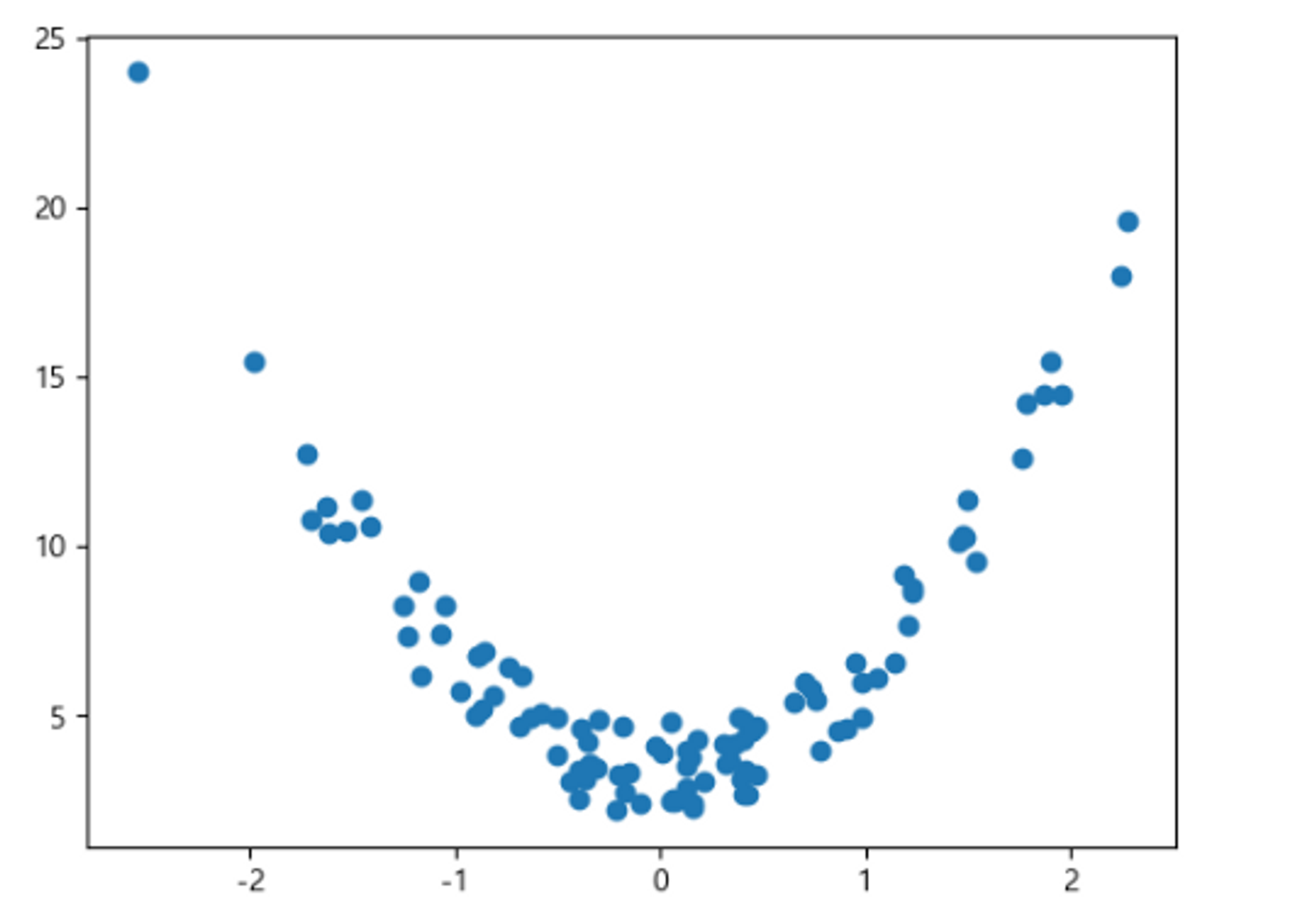
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
# activation 함수를 사용하지 않은 모델
# 빈 모델 생성.
model1 = keras.Sequential()
# 모델에 Layer들 추가
# input_shape=(1, )는 입력데이터의 형태로 (1, )은 하나의 숫자를 입력으로 받는 형태를 나타낸다.
# 따라서 model1.add(layers.InputLayer(input_shape=(1, )))는 하나의 숫자를 입력으로 받는 입력층을 모델에 추가하는 것을 의미한다.
# 첫번째 층을 만드는 것.
model1.add(layers.InputLayer(input_shape=(1, )))
# Hidden Layer
# Unit을 10개로 지정
model1.add(layers.Dense(10))
# Output Layer
# 추론값이 1개이므로 unit을 1개로 지정.
model1.add(layers.Dense(1))
# 모델 컴파일
model1.compile(optimizer='adam', loss='mse')
# 모델 학습
# 200번 학습시킬 것이다.
model1.fit(X, y, epochs=200) ⇒ loss: 줄어든 것을 확인할 수 있다.
⇒ loss: 줄어든 것을 확인할 수 있다.
손실함수(Loss function, 비용함수)
- 손실 함수는 실제값(ground truth)과 모델의 예측값 사이의 차이를 측정하여 모델의 오차를 정량화한다.
다양한 문제 유형에 따라 다른 손실 함수가 사용될 수 있다.
- 손실함수 종류
Classification (분류)
log loss 사용 => 𝑙𝑜𝑔(모델이출력한정답에대한확률)
- Binary classification (이진 분류)
- 이진 분류 문제에서 사용되는 손실 함수로, 실제값과 예측값 사이의 차이를 로그 함수를 사용하여 계산
수식: 𝐿𝑜𝑠𝑠(𝑦̂ (𝑖),𝑦(𝑖))=−𝑦(𝑖)𝑙𝑜𝑔(𝑦̂ (𝑖))−(1−𝑦(𝑖))𝑙𝑜𝑔(1−𝑦̂ (𝑖))
𝑦(𝑖): 실제 값(Ground Truth)
𝑦̂ (𝑖): 예측확률
- Multi-class classification (다중 클래스 분류)
- 두 개 이상의 클래스를 분류하는 것 (여러개 중 하나)
- categorical_crossentropy를 loss function으로 사용
수식: 𝐿𝑜𝑠𝑠(𝑦̂ (𝑖)𝑐,𝑦(𝑖))=−∑𝑐=1𝐶𝑦(𝑖)𝑐𝑙𝑜𝑔(𝑦̂ (𝑖)𝑐)
𝑦(𝑖): 실제 값(Ground Truth)
𝑦̂ (𝑖)𝑐: class별 예측확률
- Regression (회귀)
- 연속형 값을 예측한다.
- Mean squared error를 loss function으로 사용
수식: 𝐿𝑜𝑠𝑠(𝑦̂ (𝑖),𝑦(𝑖))=1/2(𝑦̂ (𝑖)−𝑦(𝑖))2
𝑦(𝑖): 실제 값(Ground Truth)
𝑦̂ (𝑖): 예측 값
<정리>
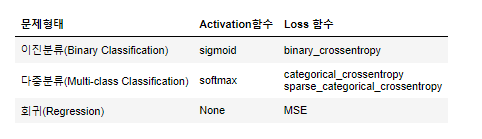
Optimizer (최적화 방법)
-
Training 시 Loss function이 출력하는 값을 줄이기 위해 파라미터(weight, bias)를 update 과정을 최적화(Optimization) 이라고 한다.
-
Training시 모델 네트워크의 parameter를 데이터에 맞춰 최적화 하는 알고리즘이다.
최적화의 종류
- Gradient Decent(경사하강법)
- 최적화를 위해 파라미터들에 대한 Loss function의 Gradient값을 구해 Gradient의 반대 방향으로 일정크기 만큼 파라미터들을 업데이트 하는 것
수식 𝑊𝑛𝑒𝑤=𝑊−𝛼(∂/∂𝑊)𝐿𝑜𝑠𝑠(𝑊)
𝑊:파라미터
𝛼:학습률
- 오차 역전파(Back Propagation)
- 딥러닝 학습시 파라미터를 최적화 할 때 추론한 역방향으로 loss를 전달하여 단계적으로 파라미터들을 업데이트한는 방법이다.
- 출력에서 입력방향으로 계산하여 역전파(Back propagation)라고 하는 것이다.
오차 역전파를 이해하기위해서는 계산 그래프를 이해하여야 한다.
- 계산 그래프 (Computational Graph)
- 복잡한 계산 과정을 자료구조의 하나인 그래프로 표현
- 그래프는 노드(Node)와 엣지(Edge)로 구성
노드: 연산을 정의
엣지: 데이터가 흘러가는 방향 - 계산 그래프 절차 및 특장점
- 계산 시작에서 계산 결과 방향으로 순서대로 계산: 순전파(Forward propagation)
- 계산 결과에서 계산 시작 역방향으로 계산: 역전파(Back propagation)
- 각 노드의 계산은 자신과 관계된 정보(입력 값들)만 가지고 계산한 뒤 그 결과를 다음으로 출력
=> 딥러닝에서 역전파를 이용해 각 가중치 업데이트를 위한 미분(기울기) 계산을 효율적으로 할 수 있으며, 중간 계산결과를 보관할 수 있다.
" 우리가 지금까지 계산 한것들은 모두 합성함수 인것을 알 수 있겠는가? "
특히 최적화에서는 합성함수를 이용하여 미분을 적용하는데
적용되는 풀이과정을 살펴보자.
합성함수의 미분
-
합성함수: 여러 함수로 구성된 함수
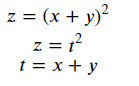
-
연쇄 법칙(Chain Rule)
- 합성함수의 미분은 합성함수를 구성하는 각 함수의 미분의 곱으로 나타낼 수 있다.
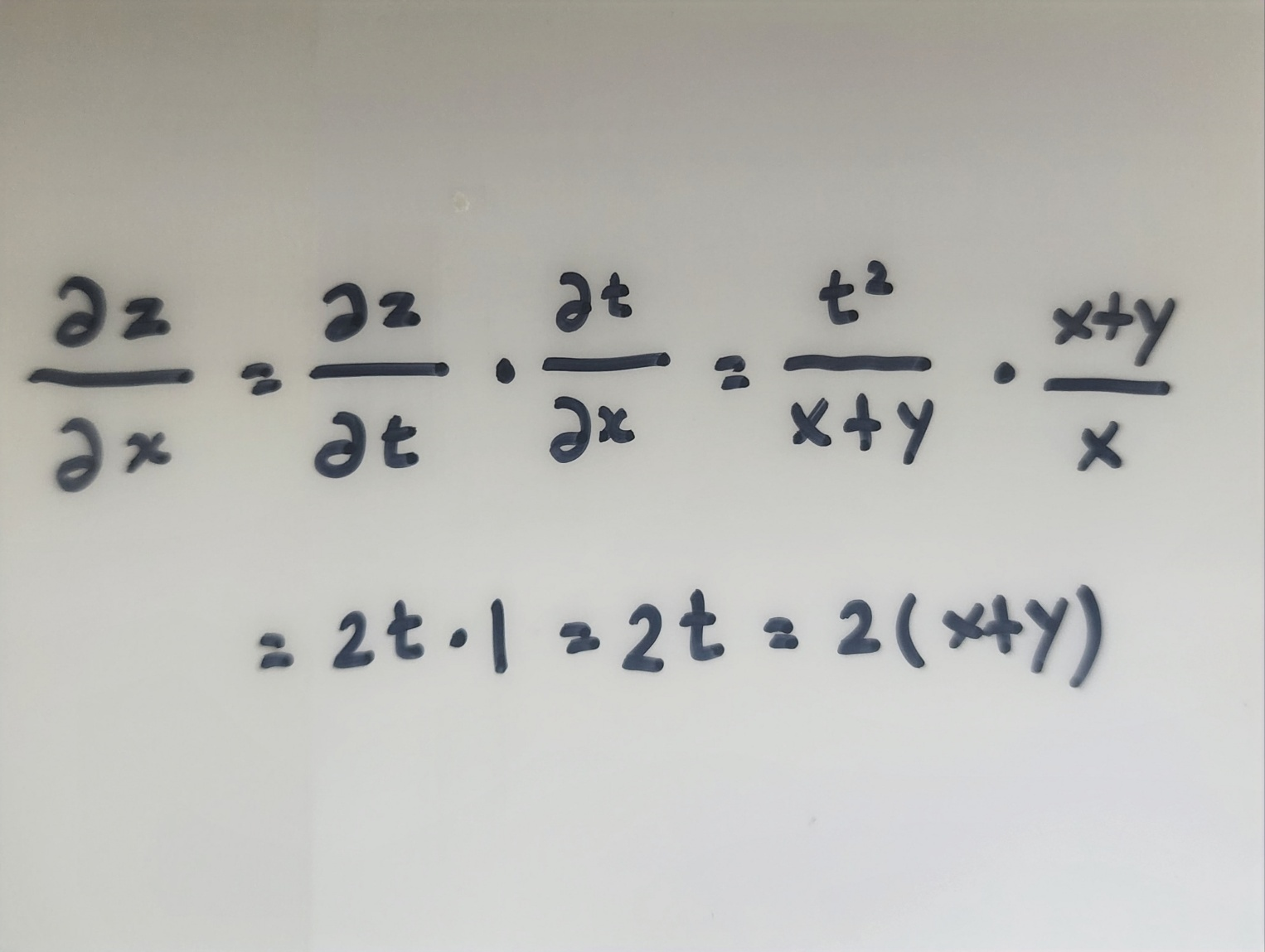
- 합성함수의 미분은 합성함수를 구성하는 각 함수의 미분의 곱으로 나타낼 수 있다.
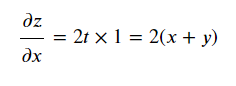
<오차 역전파 정리>
- 가중치와 편향 초기화:
- 가중치: 𝑤1, 𝑤2, 𝑤3
- 편향: 𝑏1, 𝑏2, 𝑏3
- 순전파 (Forward Propagation):
- 은닉층의 첫 번째 뉴런 값:
- 입력: 𝑥
- 활성화 함수: 𝑎1 = 𝜎(𝑤1 * 𝑥 + 𝑏1)
- 은닉층의 두 번째 뉴런 값:
- 입력: 𝑥
- 활성화 함수: 𝑎2 = 𝜎(𝑤2 * 𝑥 + 𝑏2)
- 출력층의 뉴런 값:
- 입력: 𝑎1, 𝑎2
- 활성화 함수: 𝑦̂ = 𝜎(𝑤3 𝑎1 + 𝑤4 𝑎2 + 𝑏3)
- 은닉층의 첫 번째 뉴런 값:
- 손실 함수 계산:
- 평균 제곱 오차: 𝐿 = (𝑦̂ - 𝑦)²
여기서 이제 본격적으로 오차 역전파를 이용방법을 알아보자.
- 오차 역전파 (Backpropagation):
- 출력층 오차:
- ∂𝐿/∂𝑦̂ = 2(𝑦̂ - 𝑦)
- 출력층 가중치와 편향의 업데이트:
- ∂𝐿/∂𝑤3 = ∂𝐿/∂𝑦̂ * 𝑎1
- ∂𝐿/∂𝑤4 = ∂𝐿/∂𝑦̂ * 𝑎2
- ∂𝐿/∂𝑏3 = ∂𝐿/∂𝑦̂
- 은닉층 오차:
- ∂𝐿/∂𝑎1 = (∂𝐿/∂𝑦̂ 𝑤3) 𝜎'(𝑤1 * 𝑥 + 𝑏1)
- ∂𝐿/∂𝑎2 = (∂𝐿/∂𝑦̂ 𝑤4) 𝜎'(𝑤2 * 𝑥 + 𝑏2)
- 은닉층 가중치와 편향의 업데이트:
- ∂𝐿/∂𝑤1 = ∂𝐿/∂𝑎1 * 𝑥
- ∂𝐿/∂𝑤2 = ∂𝐿/∂𝑎2 * 𝑥
- ∂𝐿/∂𝑏1 = ∂𝐿/∂𝑎1
- ∂𝐿/∂𝑏2 = ∂𝐿/∂𝑎2
- 출력층 오차:
- 경사하강법을 사용하여 가중치와 편향 업데이트:
- 𝑤1 = 𝑤1 - 𝛼 * ∂𝐿/∂𝑤1
- 𝑤2 = 𝑤2 - 𝛼 * ∂𝐿/∂𝑤2
- 𝑤3 = 𝑤3 - 𝛼 * ∂𝐿/∂𝑤3
- 𝑤4 = 𝑤4 - 𝛼 * ∂𝐿/∂𝑤4
- 𝑏1 = 𝑏1 - 𝛼 * ∂𝐿/∂𝑏1
- 𝑏2 = 𝑏2 - 𝛼 * ∂𝐿/∂𝑏2
- 𝑏3 = 𝑏3 - 𝛼 * ∂𝐿/∂𝑏3
<정리>
[경사하강법과 오차 역전파의 차이점]
졍사하강법은 순전파로 입력에서 출력으로 향하며 가중치믈 업데이트 한다.
but
오차 역전파는 순전파에서 부터 손실함수까지 계산 후 -> 오차 역전파를 적용하여 출력층 오차 -> 출력층 가중치와 편향 업데이트 -> 은닉층 가중치와 편향 업데이트 -> 경사하강법을 이용한 가중치와 편향업데이트처럼 역으로 계산하여 가중치뿐만이니라 편향(bias)까지 업데이트한다.