
디지털 신호 처리 연구의 기반이 되는 선수과목, '신호및시스템' 내용을 복습하기 위해 쓴 글입니다. 내용에 오류가 있을 시, 조언 및 지적해주시면 감사하겠습니다.
Classification of signals
1. Continuous time & Discrete time ✅
2. Real & Imaginary ✅
3. Periodic & NonPeriodic ✅
4. Even & Odd
5. Energy & Power
6. Deterministic & Random
🧡 Continuous time & Discrete time
Continuous time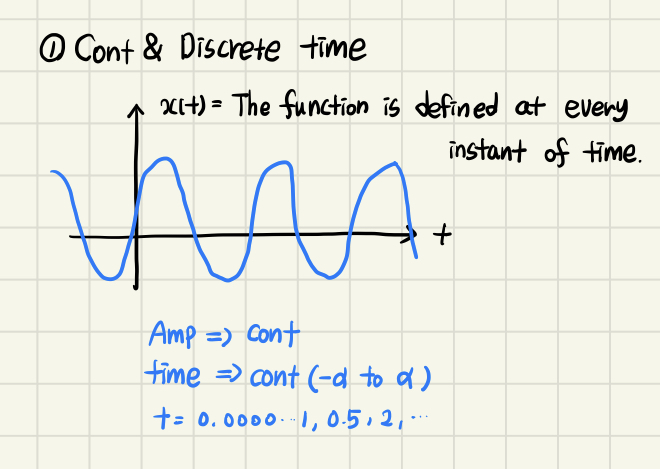
- 모든 시간 t에 대해 함수가 정의된다.
Discrete time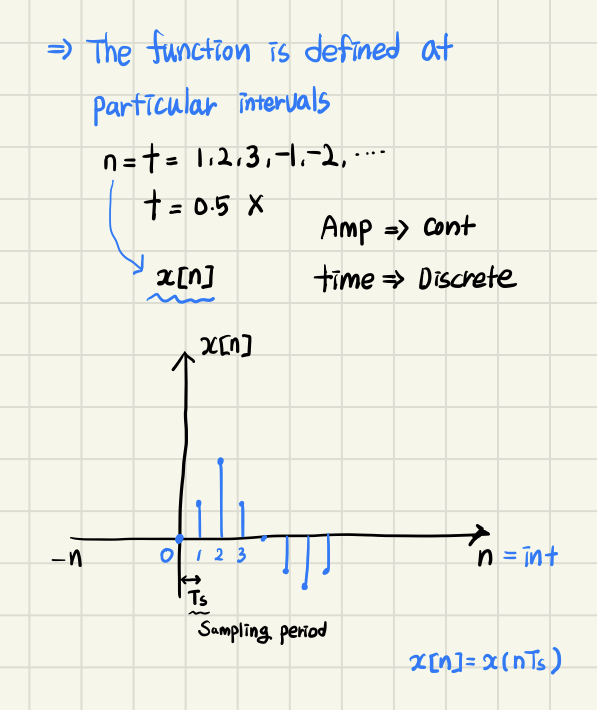
- 특정 시간 t에 대해 일정한 간격으로 함수가 정의된다.
🧡 Real & Imaginary
- 일 때, ➡️ Real Signal
- 일 때, ➡️ Odd Signal
- Real Signal이라면 허수부가 0이 되어야하고 Imaginary Signal이라면 실수부가 0이 되어야 한다.
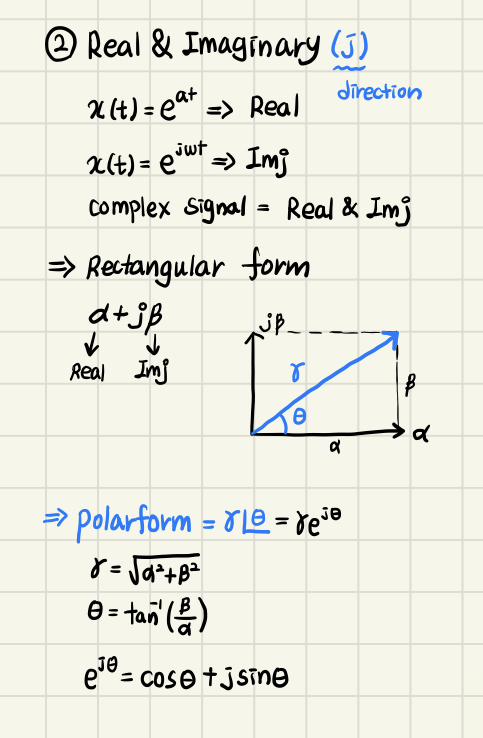
- Complex Signal은 실수부와 허수부를 모두 가지고 있는 신호이다.
- 공식을 통해 를 유도할 수 있다.
🧡 Periodic and Aperiodic(AP) signal
- Periodic Signal: 주기성을 가지고 있는 신호
- Aperiodic(AP) Signal: 주기성을 가지고 있지 않고 패턴화 되지 않는 신호
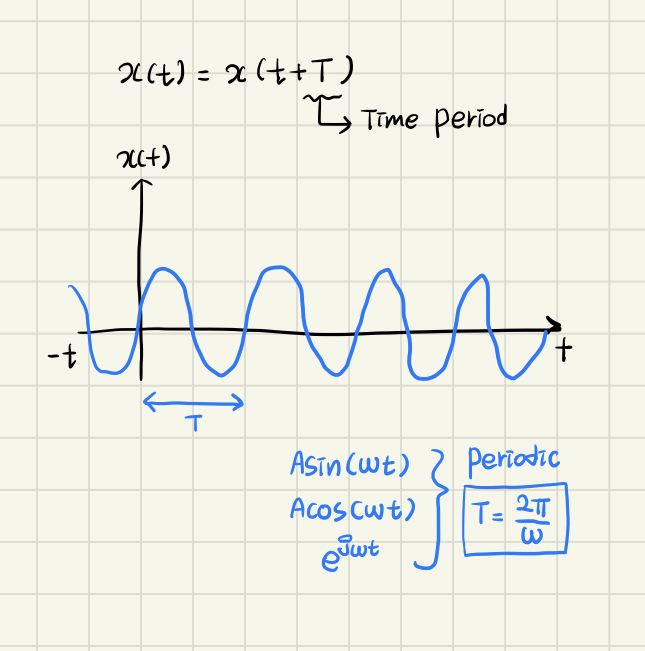
-
T는 Time Period를 의미하며

-
➡️ 2개 이상의 함수들로 이루어진 신호의 주기를 구해보자!
- 각 함수별 시간 주기를 구한다.
- 을 각 주기로 나눈다. 이때 유리수(rational number)로 나타낼 수 있으면 는 periodic 함수이다.
- 과정 2에서 구한 값에 을 곱한 값이 이 된다.

-
과정 2의 결과가 유리수()이므로 Periodic signal이다.

-
과정 2의 결과가 무리수()이므로 Aperiodic signal이다.
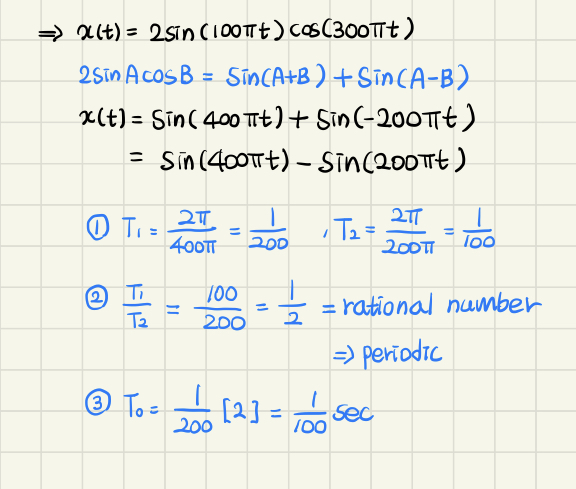
-
과정 2에서 분모의 최소공배수가 2이므로 과정 3에서 값에 2가 곱해진다.
Periodity of Discrete time signals
- Discrete time의 경우 m은 N을 정수로 변환하는데 필요한 최소 정수값, N은 time period 안에 존재하는 샘플들의 개수를 의미한다.

- 의 값이 유리수(rational number)라면 신호가 periodic한 성질을 갖는다고 할 수 있으며 m과 N의 추정값을 구할 수 있다.

- 식의 결과값이 무리수이므로 AP 신호이다.
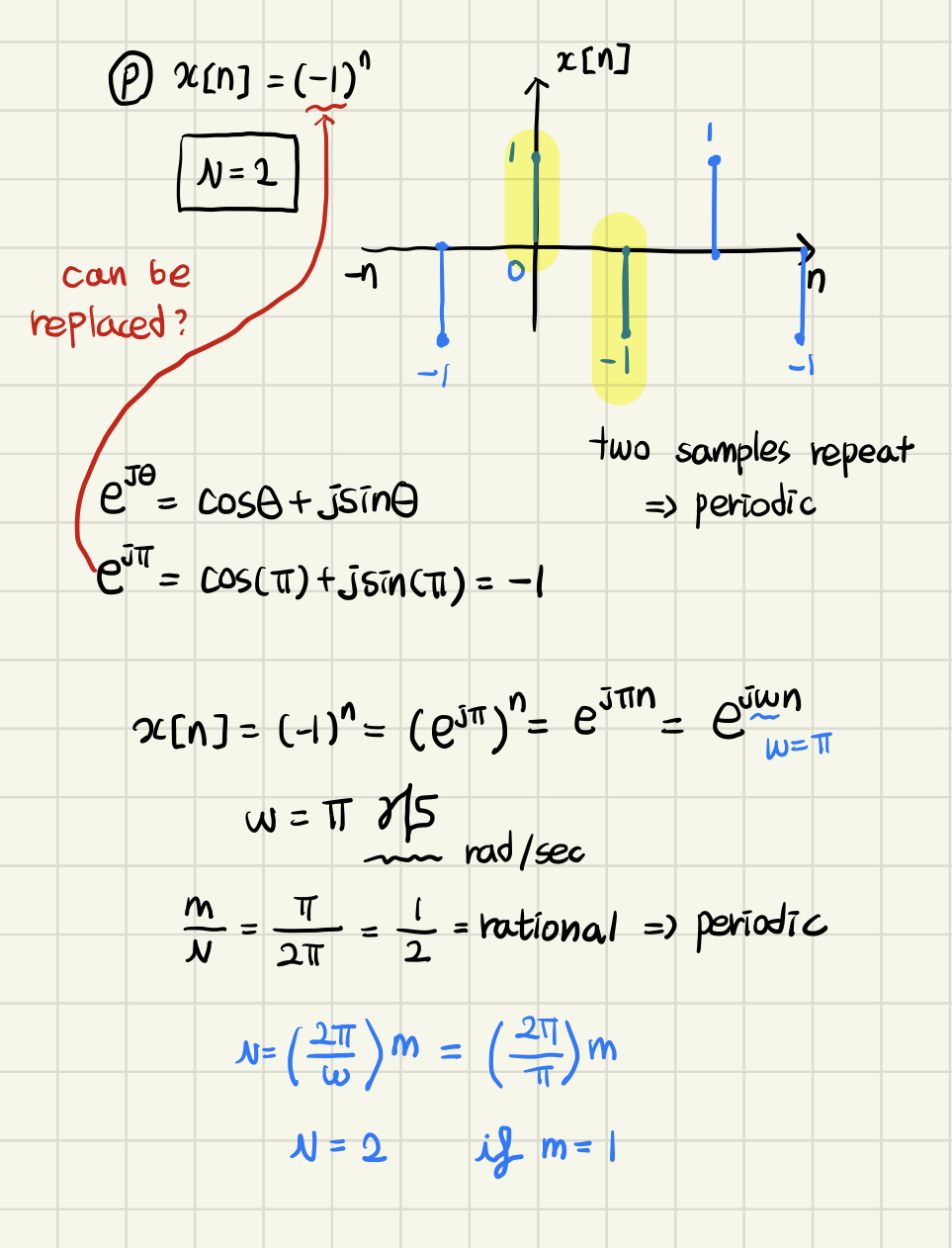
- ➡️ 을 로 바꿀 수 있다.
- ➡️ 는 로 바꿀 수 있다.
- 로 유리수가 나오므로 이 신호는 Periodic하다.
