신호의 분류(2)

디지털 신호 처리 연구의 기반이 되는 선수과목, '신호및시스템' 내용을 복습하기 위해 쓴 글입니다. 내용에 오류가 있을 시, 조언 및 지적해주시면 감사하겠습니다.

Classification of signals

1. Continuous time & Discrete time ✅
2. Real & Imaginary ✅
3. Periodic & NonPeriodic ✅
4. Even & Odd ✅
5. Energy & Power ✅
6. Deterministic & Random ✅

---

🧡 Even and Odd signals

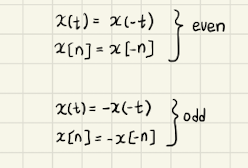
• $x(t)=x(-t)$ 부호가 같다면 even signal 이다.
• $x(t)=-x(-t)$ 부호가 다르다면 odd signal 이다.

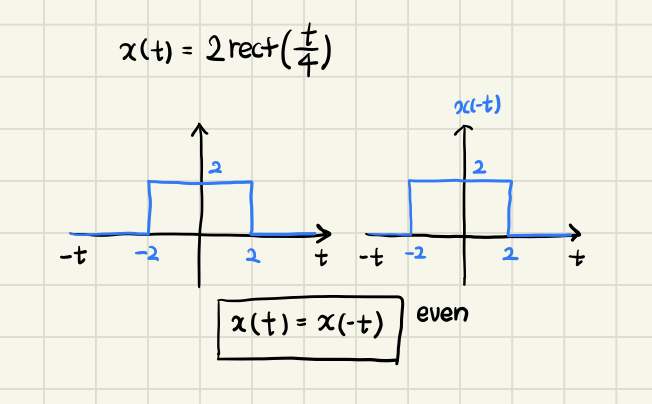
• $x(t)=2rect(\frac{t}{4})$의 경우, 세로 축을 기준으로 folding 하면 기존의 함수식과 동일한 것을 확인할 수 있다. ➡️ $x(t)=x(-t)$ ➡️ even signal

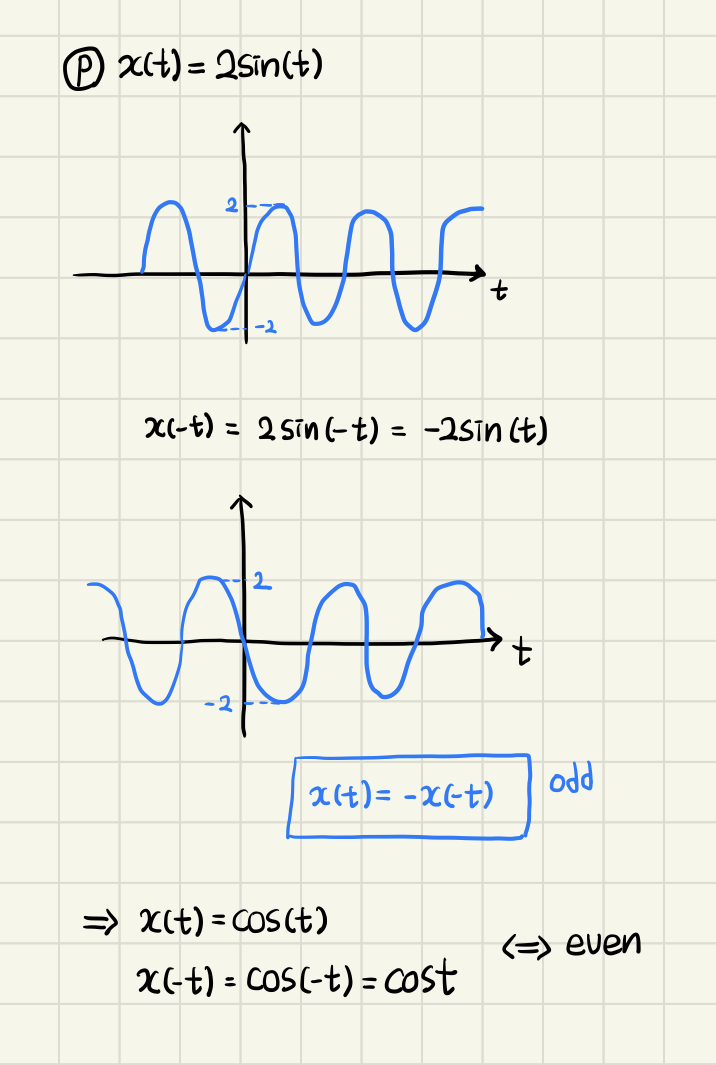
• $x(t)=2sin(t)$의 경우, 세로 축과 가로 축(t축)을 기준으로 folding 하면 기존의 함수식과 동일한 것을 확인할 수 있다. ➡️ $x(t)=-x(-t)$ ➡️ odd signal
• $x(t)=cos(t)$의 경우, 가로 축(t축)을 기준으로 folding 하면 기존의 함수식과 동일한 것을 확인할 수 있다. ➡️ $x(t)=x(-t)$ ➡️ even signal

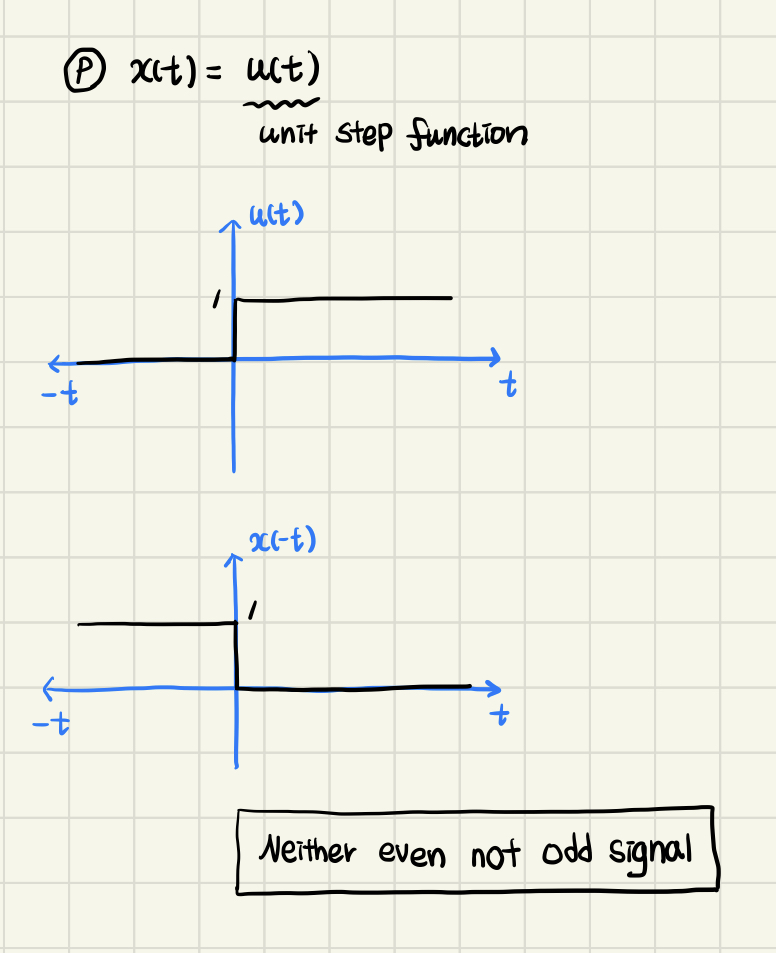
• 위와 같은 unit step function인 $u(t)$는 even signal도 아니고 odd signal도 아니다.

Problems on Even and Odd signal

$x(t)=x_{e}(t)+x_{o}(t)$
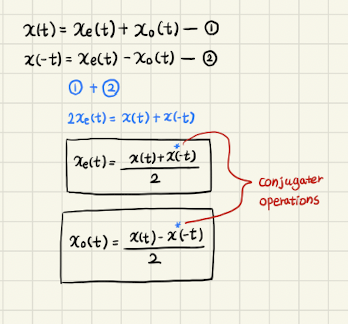
$x(-t)=x_{e}(t)-x_{o}(t)$ 을 가정해보자.

두 식을 더하면, $2x_{e}(t)=x(t)+x(-t)$ 란 식이 나온다.
위 식은 even, odd signal에 따라 다음과 같이 분리 될 수 있다.

• $x_{e}(t)=\frac{x(t)+x^*(-t)}{2}$
• $x_{o}(t)=\frac{x(t)-x^*(-t)}{2}$

+) * 는 conjugate operation을 나타낸다. conjugate에는 '짝으로 결합한'이라는 뜻으로, a+bi와 a-bi가 '짝으로 결합해' 있는 것을 예시로 볼 수 있다.

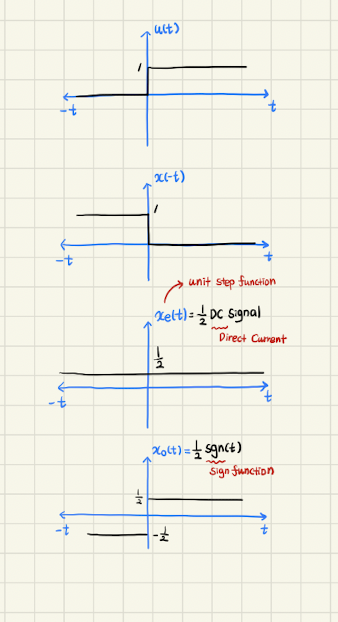위 그래프에서 첫 번째 두 번째 식은 even, odd signal을 나타내고 있지 않다. 3번째 식은 even signal을, 4번째 식은 odd signal을 각각 나타내고 있는 것을 확인할 수 있다.

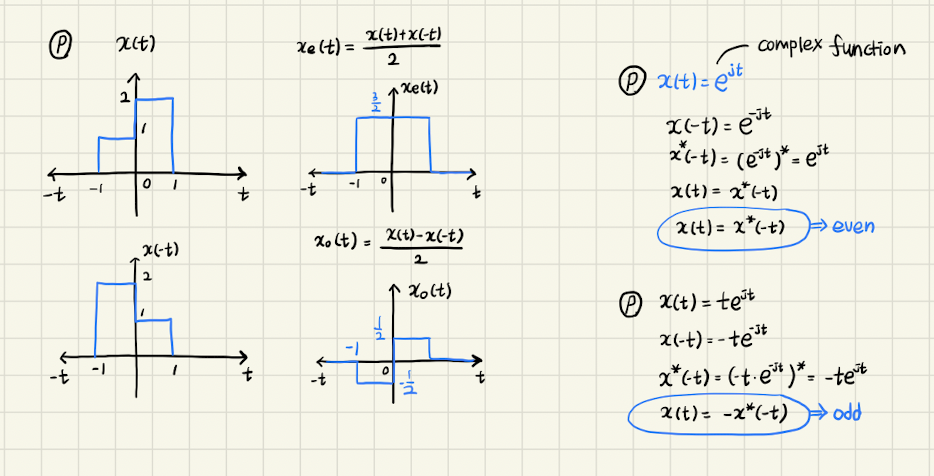
• $x(t)=e^{jt}$의 경우, $x(t)=x^*(-t)$이므로 even signal이다.
• $x(t)=te^{jt}$의 경우, $x(t)=-x^*(-t)$이므로 odd signal이다.

🧡 Energy and Power signal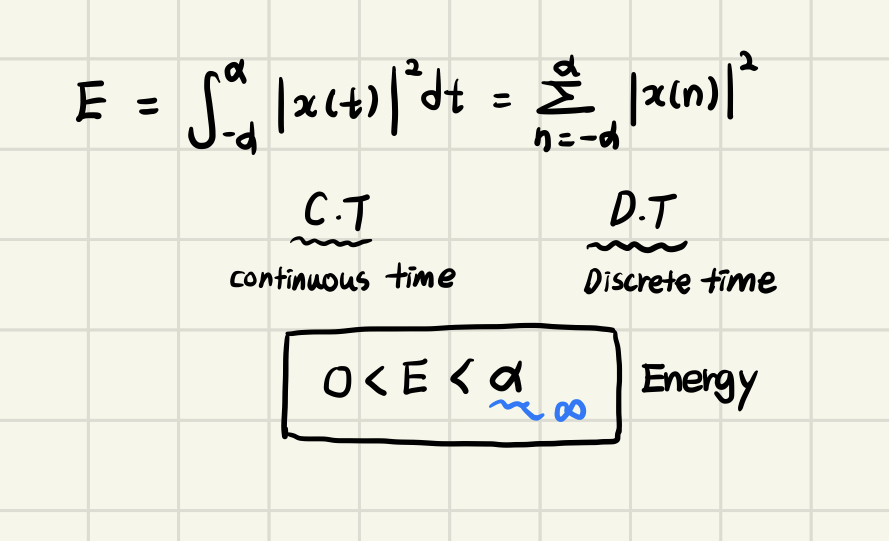

에너지 값은 위와 같은 식으로 나타낼 수 있다. ($\alpha=\infty$)
에너지는 0 < E < $\alpha$ 조건식을 만족해야 한다.

• Continous time ➡️ $\int_{-\alpha}^{\alpha}|{x(t)|^2dt}$
• Discrete time ➡️ $\sum_{n=-\alpha}^{\alpha}|{x(n)|^2}$

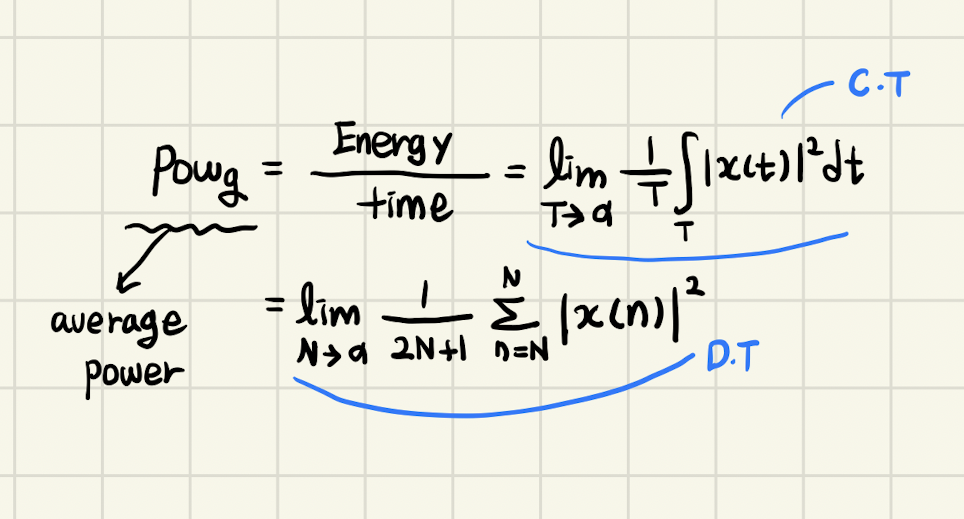Power의 평균값은 $\frac{Energy}{Time}$ 을 통해 구할 수 있다.

• Continous time ➡️ $\lim_{T \to \alpha}\frac{1}{T}\int_{T}|{x(t)|^2dt}$
• Discrete time ➡️ $\lim_{N \to \alpha}\frac{1}{2N+1}\sum_{n=N}^{N}|{x(n)|^2}$

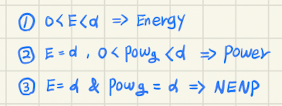
• 0 < E < $\alpha$ 이면 Energy signal이다.
• E = $\alpha$ 이고 0 < $Pow_{g}$ < $\alpha$ 이면, Power signal이다. (power signal의 energy는 $\alpha$ 이다.)
• E = $\alpha$ 이고 $Pow_{g}$ 도 $\alpha$ 라면, energy도 아니고 power signal도 아니다.

Problems on Energy and Power signal

위 식의 결과값이 $E=\frac{1}{2a}$로 이 값은 $\alpha(=\infty)$보다 작으므로 위 함수식은 Energy signal을 나타낸다.

위 식의 결과값이 $E=\alpha$, $Pow_{g}$ < $\alpha$를 만족하므로 위 함수식은 Power Signal을 나타낸다.

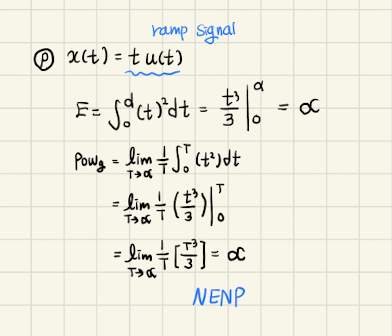위 식의 결과값이 $E=\alpha$, $Pow_{g}=\alpha$를 만족하므로 위 함수식은 Engergy Singal도 아니고 Power Signal도 아니다.

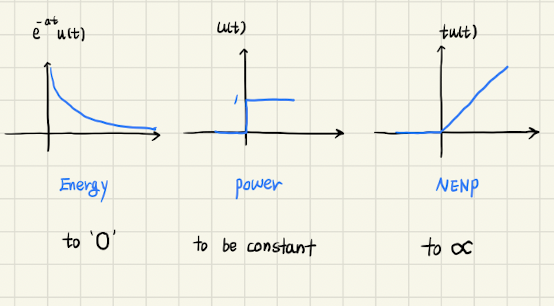순서대로 위 문제들의 나타낸 그래프이다.

• Energy Signal은 0을 향해 나아간다.
• Power Signal은 0이 아닌 특정 값으로 일정(constant)하게 나아간다.
• NENP(Engergy도 Power Signal도 아님)는 무한대를 향해 나아간다.

Problems on discrete time signal

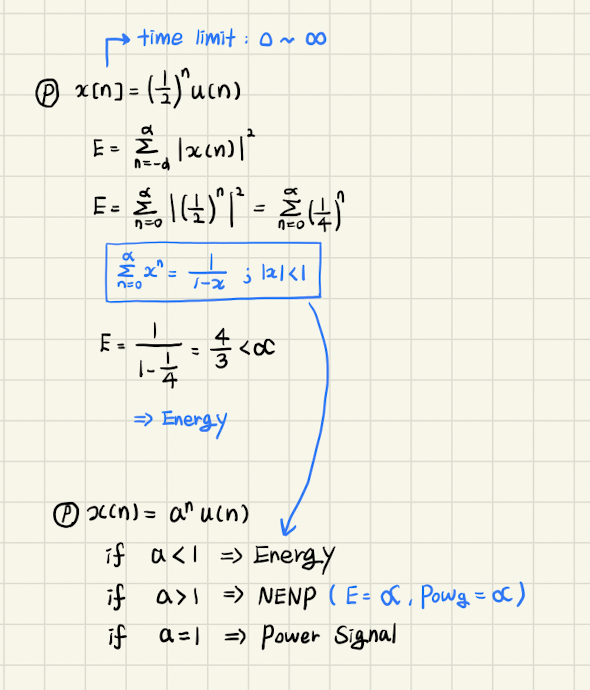무한 등비 급수 공식을 이용하여 위 식이 나타내는 신호가 무엇인지를 알 수 있다.

무한등비 급수 공식 : $\sum_{n=0}^{\alpha}{x^n}=\frac{1}{1-x}; |x|<1$

$x(n)=a^n u(n)$ 을 가정해보자.

• $a<1$ 이면, Energy Signal이다. (0 < E < $\alpha$)
• $a>1$ 이면, NENP 이다. ($E=\alpha$, $Pow_{g}=\alpha$)
• $a=1$ 이면, Power Signal이다. ($E=\alpha$, 0 < $Pow_{g}$ < $\alpha$)

🧡 Deterministic and Random signal

• 'Deterministic'이란 의미는 식으로 정립이 가능하고 이를 통해 예측 가능하다는 뜻이다.

random signal은 예측 불가능하며 식으로 나타낼 수 없다. 신호는 다음과 같이 분류할 수 있다.