대수적으로 문제를 풀기 어려울 때나 상황이 잘 이해가 안 될 때 기하학적인 직관을 가지고 생각하면 생각보다 쉽게 이해가 되는 경우가 많다. 불행히도 차원이 높아지면 우리가 생각한 직관이 뒷통수를 때리기도 한다.
상자에 공을 넣었는데 공이 상자보다 커졌어요...
또 이상한 말을 하는 거 같지만, 재밌는 상상을 해보면 재밌는 결과가 나온다. 변의 길이가 1cm인 정사각형을 생각하자.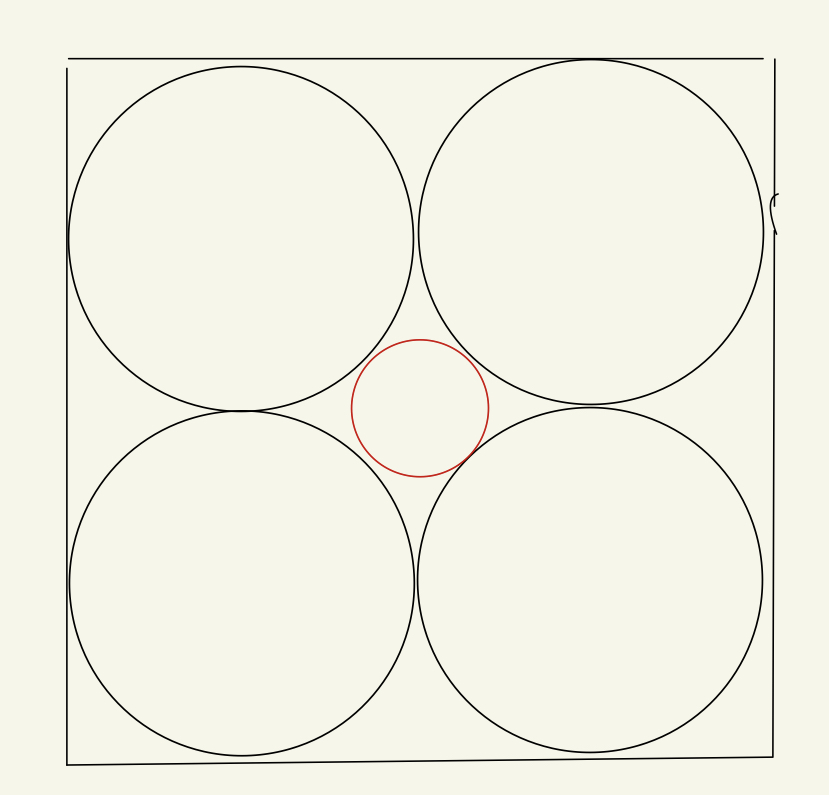
(조금 여백이 있어 불편하기 하지만....)
무슨 그림이냐면 사각형의 네 귀퉁이마다 흰 공을 넣고 가운데 비는 곳에 빨간 공을 넣은 것이다.
이때 생각하고자 하는 것은 빨간 공의 지름이다. 여러가지 방법으로 구할 수 있겠지만 가장 쉽다고 생각하는 방법은 아래와 같다.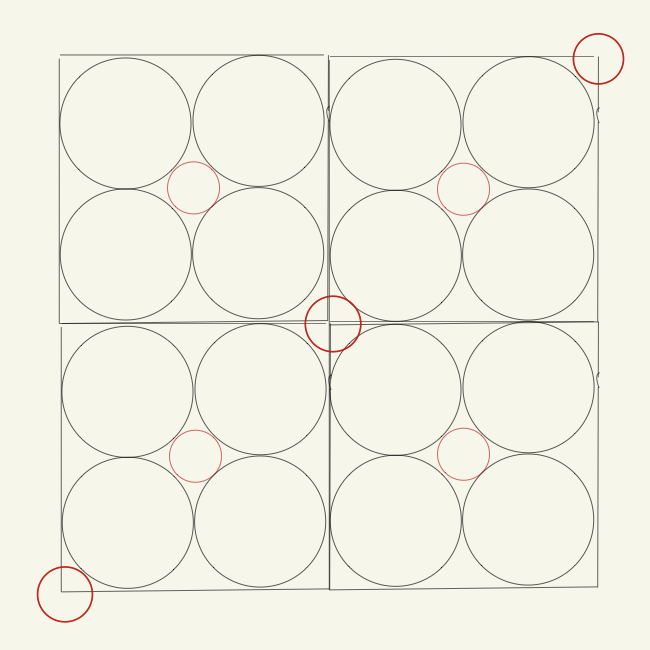
이러면 한 정사각형의 대각선 길이는 빨간 공 두 개와 흰 공 두 개의 지름 합이 된다.
당연히 빨간 공의 지름은 상자보다 작다. 우리의 직관과 잘 부합한다.
차원을 높이면?
차원을 높여보자. 그러면 유감스럽게 구를 그려야 하는데...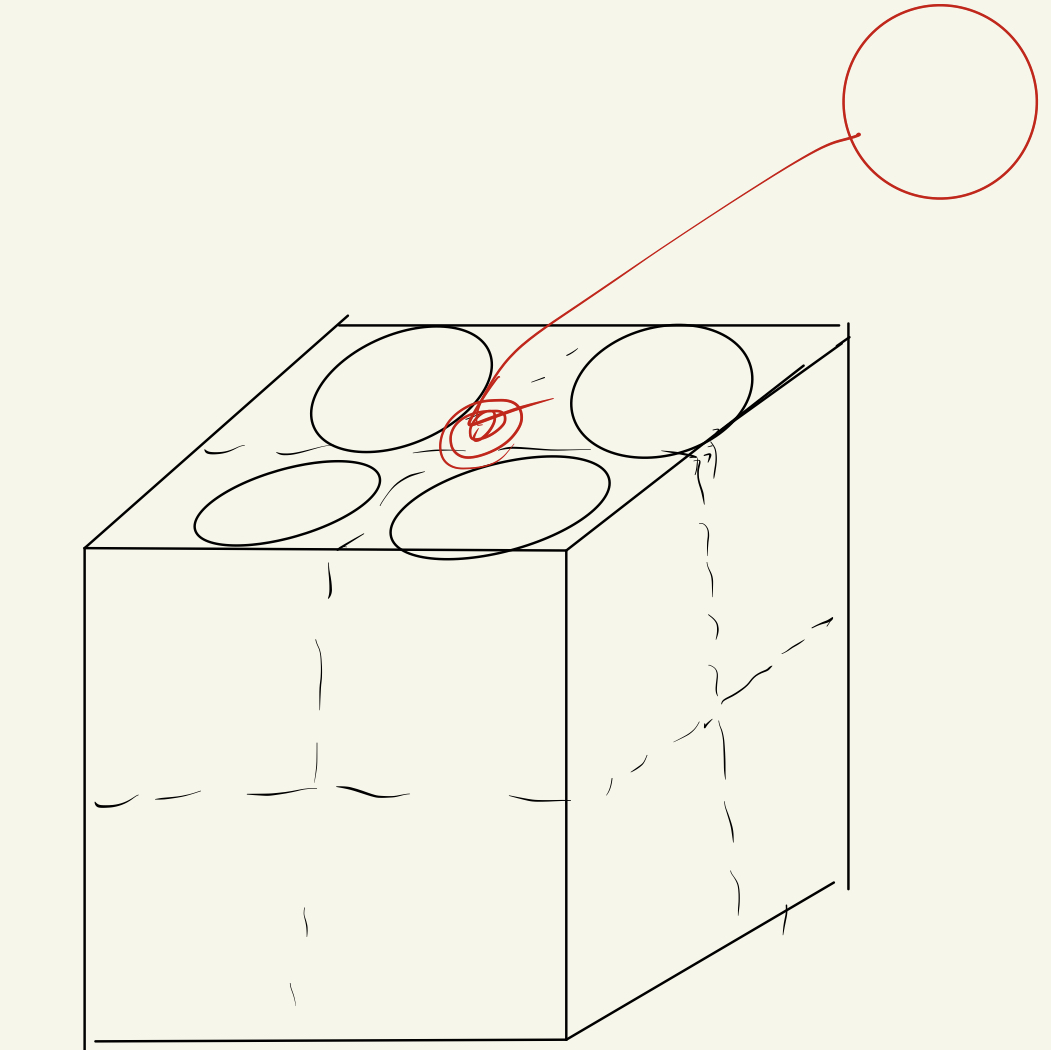
음 이게 뭔 그림이냐면... 저 점선으로 된 정육면체에 흰 공이 하나씩 들어있다고 생각하면 된다. 그 사이에 빈 공간에 빨간 공이 들어가는 모양이다. 1차원 그림을 2층으로 확장 시켰다 생각하면 편할 듯 하다.
이제 빨간 공의 지름이 아까보다 커졌다!
미미하지만 계속 차원을 높이다 보면 커질 것 같다는 생각이 든다.
이를 4차원, 5차원, 6차원.....m차원으로 계속 확장하면 어떻게 될까? 그림은.... 그만 그리자. 아마 그림 보는 것보다 머리로 생각하는 것이 더 도움 될 법도 하다.
결론
이를 m차원으로 확장하면 m차원 상자를 가로지르는 빗변의 길이는 피타고라스 정리에 의해 모든 변 제곱합의 루트를 씌운 게 된다. 피타고라스 정리 확장이라 생각하면 조금 쉬울 수 있다(제곱항이 두 개에서 3,4,5개....로 추가)
이제 m차원에 대한 위 공식의 일반 해를 구하면 다음과 같다:
9차원 이상으로 상자를 키우면 지름이 상자의 길이 이상 되는 것을 볼 수 있다. 따라서 정말 굳이 코끼리를 냉장고에 넣고 싶으면 적당한 크기의 냉장고를 골라 차원을 높여주면 되겠다.
마무리
이렇게 고차원에서 우리의 직관이 틀릴 수 있다는 것을 예시를 통해 확인했다. 이런 말장난 같은 것이 사실은 머신러닝과 딥러닝에 연관이 되어 있다. XOR 문제를 차원을 높임으로써 해결하기도 하며 GAN의 성능을 안정시키고자 Mixup을 하기도 한다. 이 과정에서 고차원을 다룰 때 우리의 직관과 달라 문제가 발생하기도 한다. 이 문제와 관련된 내용을 최대한 빨리 포스팅하는 게 목표다.
여담
시각화 잘하고 싶어서 manim을 공부해볼까 했는데 너무 귀찮다. 내가 심심할 때 포스팅하는 정도인데 그정도의 시각화를 구디..? 싶긴 하다..
선형대수 시리즈 포스팅하고 싶은데 아직 공부가 덜 되서 좀 많이 늦어질 듯하다(사실 텍스가 제일 귀찮음).
