소개
최근 'SKT FLY AI'에서 공부하며 순전파와 역전파에 대해 강의를 들으며 갑자기 '순전파 역전파를 전개해본적이 있던가?' 라는 생각이 들어 계산해보려 하니 간단한 레이어 조차 계산하지 못하였습니다.
그래서 경사하강법을 이해하고 순전파와 역전파를 구현하여 학습까지 진행하는 과정을 기록하고자 하고, 누군가에게 도움이 됐으면 하여 글을 작성해봅니다.
이번 글은 간단한 이론에 대해 얘기하고 구현에 관한 자세한 내용에 대해서는 다음 글에서 언급하겠습니다.
잘못된 내용이 있다면 얘기해주세요!
코드 구현 깃허브 : MyTorch
경사하강법이란?
경사하강법 : 딥러닝에서 사용하는 학습 알고리즘으로 목표로 하는 값과의 차이(손실 함수로 정의)를 최소화 하는 방향으로 특정 값(파라미터)의 값을 조정하는 방법
그렇다면 어떻게 차이를 최소화 하는 방향으로 값을 조정할까?
경사하강법의 핵심은 기울기에 있습니다.
기울기란?
기울기 : 특정 변수에 대한 함수 값의 변화량입니다.
도함수(Deviative), 편미분(Partial Deviative), 그래디언트(Gradient)라고도 합니다. (단, 상황에따라 사용되는 단어는 다음과 같이 달라집니다.)
- 도함수(Deviative) : 변수가 하나인 단일 변수 함수에 대해서 변수의 변화량에 따른 대한 함수의 변화량 입니다.
- 편미분(Partial Deviative) : 변수가 여러개인 다중 변수 함수에 대해서 하나의 변수의 변화량에 따른 함수의 변화량을 의미합니다.
- 그래디언트(Gradient) : 변수가 여러개인 다중 변수 함수에 대해서 각 변수의 변화량에 따른 함수의 변화량 집합(벡터)을 의미합니다.( 함수 내부의 각 변수에 대한 편미분 집합 )
조정 방법
가령, 어떤 함수의 기울기가 2라면 그 순간 함수의 값은 2만큼 커지고 있으며 -2라면 그 순간 함수의 값은 -2만큼 작아진다는 것을 의미합니다.
인공지능을 학습하기 위해서는 최소점으로 가야한다고 했으니 기울기가 양수라면 현재 값이 커지고 있으니 값이 작아지도록 반대 방향으로 가도록 해야합니다.
그래서 경사 하강법은 이 기울기의 반대(-)방향으로 향하도록 하여 최소화 하는 방향으로 값을 조정합니다.
이에 대한 식은 다음과 같습니다.
여기서 는 변화시키고자 변수의 값에 의한 Loss의 변화량을 의미합니다.
기울기 값을 통해 를 갱신하는 과정이며 (학습률)을 의미합니다. (학습률에 대한 설명은 아래에서 진행하겠습니다.)
경사하강법 시각화
아래와 같이 단일 변수 함수를 정의하고 점 에서 시작하여 최적점 으로 간다고 해봅시다.
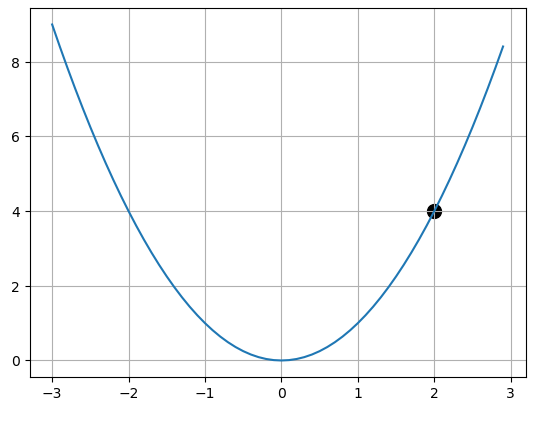
점 를 으로 이동시키기 위해서 저희는 값을 조정해야합니다.
조정하기 위해 알아야 할 값 는 로 정의 됩니다.
그럼 에 대한 기울기를 알아야 하므로 함수 를 에 대해 미분을 진행합니다.
이를 통해 점 에서의 기울기는 임을 알 수 있습니다.
이를 이용해 경사하강법 수식에 적용하면 다음과 같습니다. (이때 )
이렇게 는 새로 갱신되어 가 됩니다.
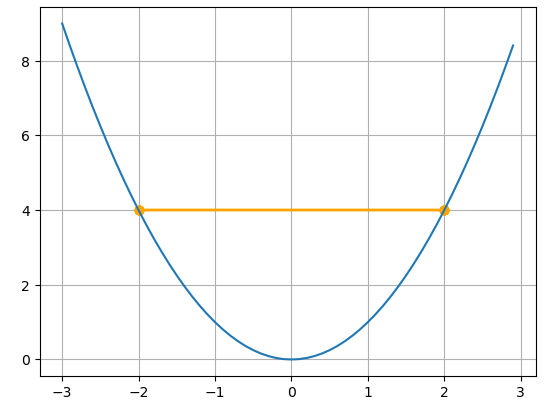
일 때에도 새로 갱신하면 인데 이러면 최적점으로 안가잖아?
특수 케이스이긴 하지만 이런 문제를 해결할 수 있도록 하는 것이 바로 학습률 입니다.
※(3,9) 에서도 가중치를 변화 시켜보시길 바랍니다.
학습률(Learning Rate)
학습률 : 기울기의 크기를 조절하여 최적점에 도달할 수 있도록 하는 사람이 직접 설정해야하는 하이퍼 파라미터
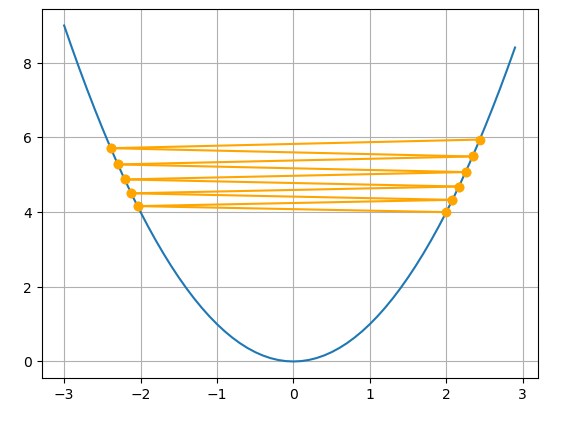
10번의 갱신(Step)과정을 통해 각 학습률에 따른 변화를 보이면 다음과 같습니다.
- 학습률이 큰 경우() : 이 경우에는 최적값으로 수렴하지 못하고 오히려 값이 커지는 방향으로 학습이 진행되는 것을 확인할 수 있습니다.
- 학습률이 작은 경우() : 이 경우에는 최적값으로 수렴하기까지 오래 걸리며 더 많은 학습을 진행해야합니다.
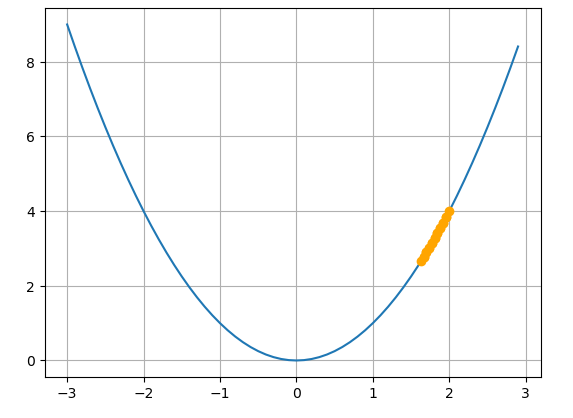
- 학습률이 적정한 경우() : 10번의 갱신만으로도 최적점에 가까워지는 모습을 확인할 수 있습니다.
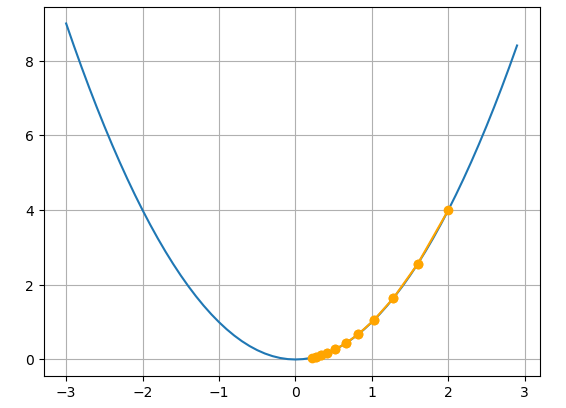
- 학습률이 최적인 경우() : 이런 경우가 발생할 가능성은 매우 희박하지만 한번의 갱신만으로도 최적점으로 향하는 것을 확인할 수 있으며 학습률의 중요성을 보여준다고 생각합니다.
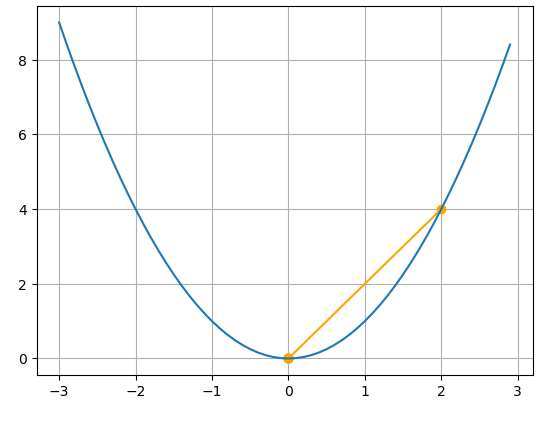
위처럼 학습률의 영향으로 인해 학습의 횟수가 달라지므로 적절한 학습률을 찾는 것은 시간적, 자원적으로 중요한 요인이 됩니다.
※위 실험에서 사용한 학습률은 일반적인 경우보다 큰 학습률입니다. 대부분 0.001 이하의 학습률을 사용하며 최적의 학습률은 실험적으로 알아내야합니다.
딥러닝에서의 경사하강법
지금까지의 내용은 경사하강법의 원리를 이해할 수 있도록 간단한 단일 변수 함수 을 예시로 드는 내용이었습니다.
딥러닝에서 대부분의 함수는 다중 변수 함수로 이루어져 있습니다.
각각 변수(가중치)를 갱신하기 위해서는 각 변수의 변화량이 함수의 변화량에 미치는 영향을 계산해야 합니다.
그래서 딥러닝에서는 편미분을 사용합니다.
편미분은 간단히 말해 목표로 하는 변수를 제외한 모든 변수를 모두 상수 취급하여 미분하는 과정입니다.
함수 설정
딥러닝에서 가장 일반적인 함수 식은 다음과 같습니다.
주의하셔아 할 점은 위 식에서 학습시킬 파라미터는 가 아닌 가중치 와 입니다. (이 부분에서 헷갈리시면 나중에 힘드실 겁니다.)
와 는 각각 1로 초기화 해주어 로 설정하겠습니다.
이후 함수 를 학습시키기 위한 데이터를 다음과 같이 준비하겠습니다.
-
입력 :
-
출력 : ()
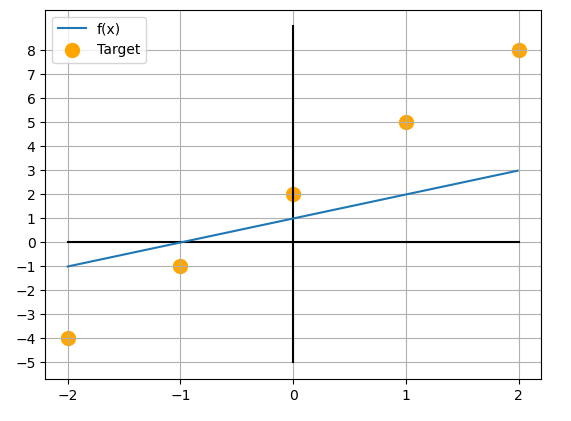
미분함수 정의
기울기를 구하기 전 학습을 하기 위해 손실함수를 다음과 같이 설정하겠습니다.
위 함수에서 는 이며 는 실제 값입니다.
따라서 최종적으로 최소화 시켜야 할 함수는 다음과 같습니다.
위에서 말했듯 얼핏 보면 위 식을 최소화 시키기 위해 를 변화시켜야할 것 같지만,
로 고정되어 있는 상수와 같기 때문에 와 를 학습시켜야 합니다.
이를 정리하면 아래와 같습니다.
를 최소화 시키기 위해서 와 값을 변화 시켜야 하기 때문에 최종적으로 편미분을 통해 와 를 구하면 다음과 같습니다.
경사하강법 적용하기
지금까지 기울기를 구하는 과정을 거쳤다면 이제는 기울기를 이용해 경사하강법으로 가중치를 갱신하는 과정을 보이겠습니다.
경사하강법을 이용해 가중치를 갱신하는 식은 다음과 같습니다.
가중치 갱신
학습률은 로 설정하여 경사 하강법을 적용하면 다음과 같습니다.
데이터 중 한 쌍()을 가져와 경사하강법을 적용하여 가중치를 갱신하면 다음과 같습니다.
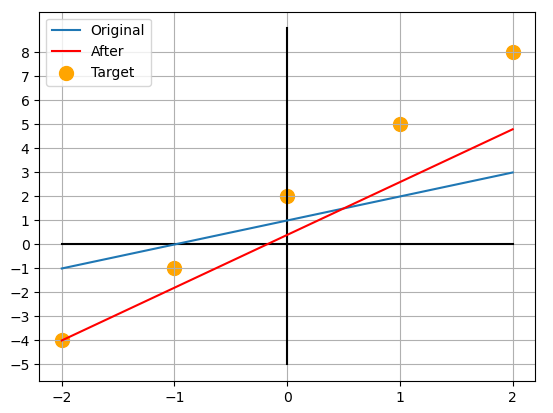
다시 한 번 데이터 중 한 쌍()을 가져와 경사하강법을 적용하여 가중치를 갱신하면 다음과 같습니다.
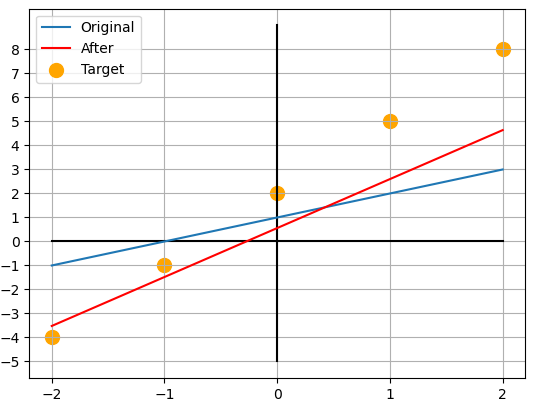
이 과정을 의 모든 값에 대해 두번 정도만 반복해준다면 가 되어 와 가까워지게 됩니다.
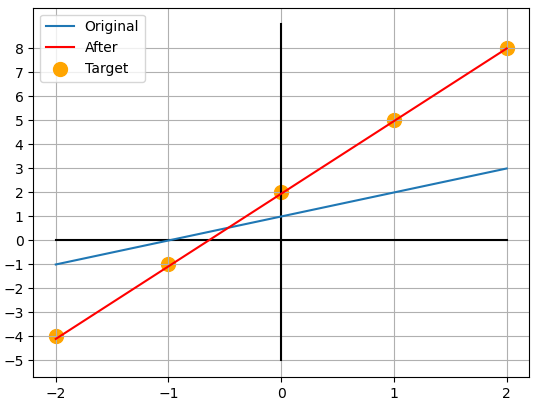
import numpy as np
import matplotlib.pyplot as plt
w=1
b=1
X = np.array([-2,-1,0,1,2])
Y = np.array([-4,-1,2,5,8])
def f(x):
return w*x+b
original = f(X)
lr = 0.1
epochs = 2
for i in range(epochs):
for j in range(len(X)):
plt.plot([-2,2],[0,0],color='black')
plt.plot([0,0],[9,-5],color='black')
plt.grid()
plt.xticks(np.arange(-2,3,1))
plt.yticks(np.arange(-5,9,1))
# 원본 그래프
plt.plot(X,original,label='Original')
x = X[j]
y = Y[j]
print("적용 전 :",w,b)
# Loss 값 구하기
loss = ((w*x+b)-y)**2
# 기울기 값 구하기
gradw = 2*x**2*w+2*b*x - 2*x*y
gradb = 2*w*x + 2*b - 2*y
# 경사 하강법 적용
w = w-lr*gradw
b = b-lr*gradb
print("기울기",gradw,gradb)
print("Loss :",loss)
print("적용 후 :",w,b)
plt.plot(X,f(X),label='After',color='r')
plt.scatter(X,Y,s=100,label='Target',color='orange')
plt.legend()
plt.show()
print()마무리
이번 글은 경사하강법에 대해서 설명을 드렸습니다.
아직은 복잡한 예시는 설명드리지 않았지만 실제로는 더 복잡한 구조와 더 많은 파라미터에 대한 연산을 가지고 있습니다.
이러한 이유로 위와 같이 함수의 미분 함수를 미리 정의하는 방식으로 경사하강법을 구현할 경우 새로운 함수를 추가할 때 많은 복잡함이 발생될 수 있는 문제점이 있습니다.
다음 글에서는 이런 복잡함을 줄일 수 있는 순전파, 역전파에 대해서 설명하도록 하겠습니다.
