소개
이전 글에서는 전체 함수와 그에 대한 미분 함수를 미리 정의 하여 각 가중치에 대한 함수의 기울기를 구하여 경사하강법을 적용하였습니다.
하지만 실제 함수는 생각보다 복잡하기 때문에 미분함수를 미리 정의하기는 어렵습니다.
이번 글에서는 위 문제점을 해결해 나아가는 과정을 설명하고 이후 순전파와 역전파에 대한 개념 설명 후 간단한 하도록 하겠습니다.
'미분함수 정의' 방법의 문제점
이전 글에서처럼 미분함수를 미리 정의 하여 각 가중치에 대한 함수의 기울기를 구하는 경우 다음과 같은 문제점이 발생합니다.
-
모델 구조 변경의 어려움 :
함수(레이어) 로 구성된 모델에 대해 새로운 함수(레이어) 를 추가하여 구조의 모델을 만든다고 할 때, 모든 가중치에 대한 미분함수 ,를 새로 정의해야합니다. -
ReLU 함수같은 함수 구현의 어려움 :
ReLU 함수의 수식은 다음과 같이 정의 됩니다.만약 복잡한 구조를 가진 함수 중간에 ReLU 함수를 넣게 된다면 ReLU 함수의 입력 값을 기록하며 이에 맞게 최종 미분 함수를 선택하도록 알고리즘을 작성해야 합니다.
'미분 공식 활용' 방법을 통한 해결
위의 문제를 간단히 미분 공식을 통해 해결할 수 있습니다.
여기서 는 0에 매우 가까운 수라고 할 때 다음과 같이 코드로 구현할 수 있습니다.
편미분 예시 코드
구하고자 하는 변수의 값만 변화시키는 방식
def diff(func,input1,input2):
ret = (func(*input1)-func(*input2))/1e-10
return ret
def f(x,y):
return x**2-2*y
eps = 1e-10
print(
diff(f,[2+eps,0],[2,0]),
diff(f,[0,2+eps],[0,2])
)
# 4.000000330961484 -2.000000165480742
def custom_relu(x):
if x>0: return 2*x
else : return 0
print(
diff(custom_relu,[1+eps],[1]),
diff(custom_relu,[-1+eps],[-1])
)
# 2.000000165480742 0.0함수를 새로 만들더라도 변수에 대한 정보만 알고 있다면 간단하게 편미분이 가능한 모습을 볼 수 있습니다.
합성함수
def composite_function(x,y):
return custom_relu(f(x,y))
print( #Custom ReLU 함수의 입력이 양수가 되는 경우
diff(composite_function,[3+eps,2],[3,2]),
diff(composite_function,[3,2+eps],[3,2])
)
# 12.000000992884452 -4.000000330961484
print( #Custom ReLU 함수의 입력이 음수가 되는 경우
diff(composite_function,[1+eps,2],[1,2]),
diff(composite_function,[1,2+eps],[1,2])
)
# 0.0 0.0두 함수를 합성하더라도 새로운 미분함수를 정의할 필요 없이 기울기값을 구할 수 있습니다.
새로운 '함수의 중복 실행' 문제점
위의 두 문제를 해결했지만 여기서 또 다른 문제점이 발생합니다.
함수의 중복 실행
합성함수 에서 각 변수 에 대한 함성함수 기울기를 구하기 위해서 함수와 함수 를 중복해서 실행하게 됩니다.
만약 전체 함수가 복잡해지고 연산이 많아질 경우에 이런 문제점은 연산속도에 악영향을 줍니다.
이를 해결하기 위해 연쇄법칙(Chain Rule)을 활용한 순전파와 역전파가 등장합니다.
연쇄법칙(Chain Rule)
연쇄법칙 : 합성함수에 대한 미분방법 중 하나로 합성 함수의 미분값은 합성함수를 구성하는 각 함수의 목표 변수에 대한 함수의 편미분값의 곱으로 표현할 수 있다.
※ 자세한 정의는 나무위키를 참고해주세요
아래와 같이 간단한 합성함수를 정의하고 에 대한 편미분을 다음처럼 표현할 수 있습니다.('단일 변수 함수'의 연쇄법칙)
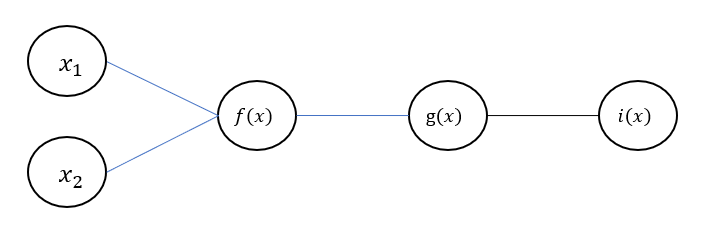
연쇄법칙은 위 과정을 다음과 같이 간단하게 여러 곱으로 표현할 수 있습니다.
위와는 달리 아래와 같이 중간에 여러 노드로 나뉘는 경우가 있을 수도 있습니다.
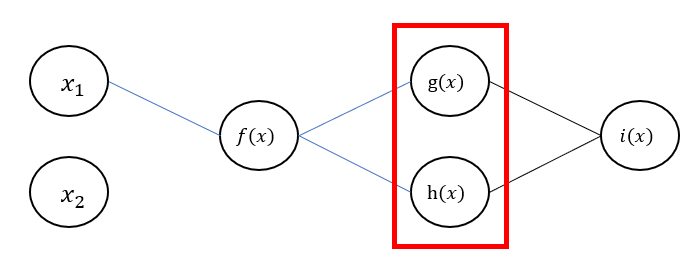
이 경우에도 에 대한 편미분을 간단하게 다음과 같이 표현할 수 있습니다.('다중 변수 함수'의 연쇄법칙)
응용 문제
위의 내용을 기반으로 을 한 번 수식으로 작성해보세요.
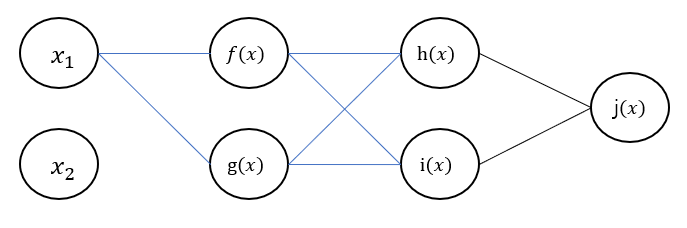
힌트
답
'함수의 중복 실행' 문제 해결
연쇄법칙이 왜 '함수의 중복 실행' 문제점을 해결할 수 있는지에 대해 설명하겠습니다.
합성함수 에 대해 와 에 대한 편미분을 연쇄법칙을 이용해 표현하면 다음과 같습니다.
이 과정에서 와 는 중복되는 값이기에 한 번만 구하면 됩니다.
이때 함수를 실행할 필요가 없기 때문에 '함수의 중복 실행'문제를 해결할 수 있습니다.
이러한 연쇄법칙을 활용해 순전파와 역전파가 이루어집니다.
순전파와 역전파
딥러닝에서 모델을 학습 하는 과정에서 순전파와 역전파는 필수입니다.
순전파 과정에서는 각 레이어에서의 그래디언트를 계산하고 저장합니다.
역전파 과정에서는 그래디언트를 이용하며 연쇄법칙을 통해 각 가중치에 대한 편미분 값을 구합니다.
순전파(Foward Propagation)
순전파 : 주어진 입력에 대해 설계한 구조에 맞게 함수들을 실행하여 결과값을 얻고 그래디언트를 계산해 저장하는 단계
가령 다음과 같이 레이어를 정의하고 설명을 진행하겠습니다.
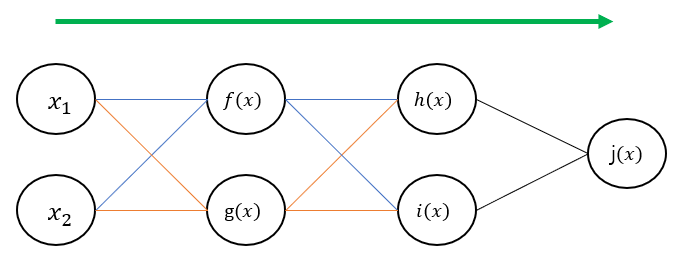
각각 함수의 그래디언트를 구하면 다음과 같습니다.
순전파 과정에서는 이 그래디언트들이 저장되며
함수 의 그래디언트를 구하는 코드는 다음과 같습니다.
def forward(func,vars):
inputs = list(vars.values())
out = func(*inputs)
grad = {}
for i,k in enumerate(vars.keys()):
inputs[i] = inputs[i]+eps
grad[k] = (func(*inputs)-out)/eps
inputs[i] = inputs[i]-eps
return out,grad
def f(w1,w2,b1,x1,x2):
return w1*x1+w2*x2+b1
eps = 1e-10
vars = {'w1':2,'w2':3,'b1':4,'x1':5,'x2':6}
forward(f,vars)
# (32,
# {'w1': 5.000018177270249,
# 'w2': 5.999964969305438,
# 'b1': 1.000017846308765,
# 'x1': 2.00003569261753,
# 'x2': 2.999982484652719})역전파(Back Propagation)
역전파 : 연쇄법칙을 활용해 기존에 구한 그래디언트를 역방향으로 곱하여 각 가중치에 대한 편미분값을 얻어내는 과정
역전파는 그냥 연쇄 법칙이라고 보시면 됩니다.
※ 연산 관점에서 역방향으로 연쇄법칙을 적용하는 방식이 더 효율적이기 때문에 역전파라고 하는 거 같습니다.
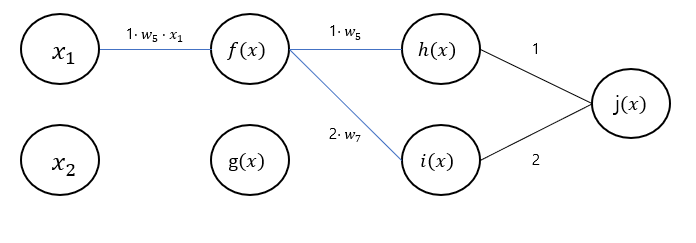
먼저 을 구하기 위해 필요한 간선들만 남기면 다음과 같습니다.
주의하실 점은 은 에만 연결되는 가중치이기 때문에 는 고려하지 않아도 됩니다.
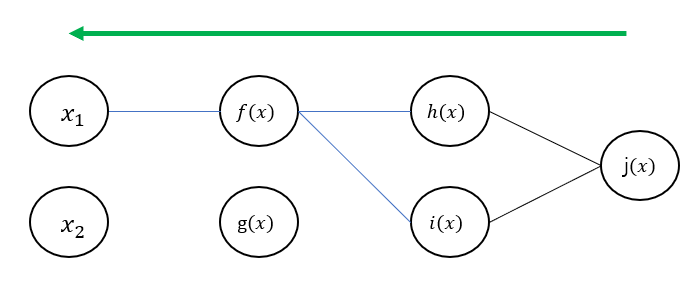
이 구조를 통해 역전파의 과정을 설명드리면 다음과 같습니다.
※ 그림의 원들을 모두 노드라고 하겠습니다.
- 노드의 그래디언트()를 연결된 변수들()에 넘겨준다.
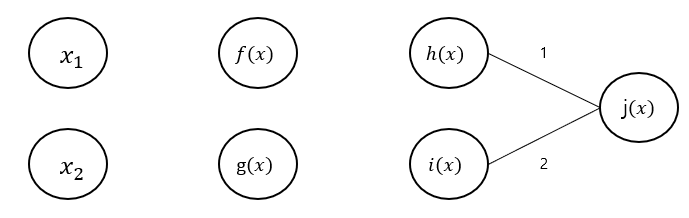
-
노드에서 다음과 같이 연산을 진행한다.
- 노드 : 노드에서 받은 그래디언트 을 현재 노드 의 그래디언트 ()에 곱하여 연결된 변수들()에 넘겨준다.
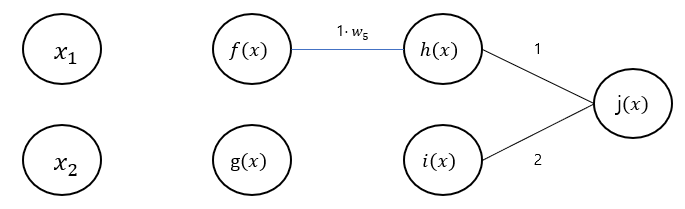
- 노드 : 노드에서 받은 그래디언트 를 현재 노드 의 그래디언트 ()에 곱하여 연결된 변수들()에 넘겨준다.
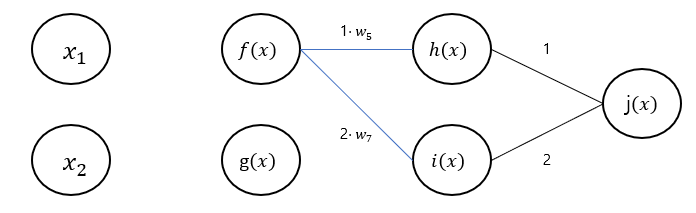
-
노드에서 다음과 같이 연산을 진행한다.
- 노드에서 받은 그래디언트 을 현재 노드 의 그래디언트 ()에 곱하여 연결된 변수들()에 넘겨준다.
- 노드에서 받은 그래디언트 을 현재 노드 의 그래디언트 ()에 곱하여 연결된 변수들()에 넘겨준다.
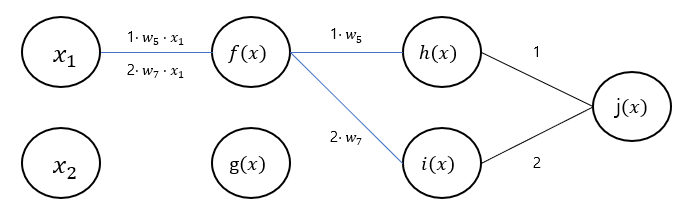
-
가중치 에서는 노드에서 받은 그래디언트들을 합하여 저장한다.
이 과정에서 가중치 뿐 아니라 위 그림과 연결된 가중치 의 그래디언트도 계산되었습니다.
비교를 위해 합성함수 를 에 대해 편미분하면 다음과 같습니다.
이를 통해 역전파의 값이 동일한 것을 확인할 수 있습니다.
다른 그래디언트들도 계산해 보시길 바랍니다.
※역전파 코드를 작성하기 위해서는 순전파까지 작성해야 하므로 다음 절에서 다루겠습니다.
순전파 역전파 코드
이번 절에서는 간단하게 순전파 역전파를 구현해보겠습니다.
- 먼저 레이어에서 다룰 변수들을 먼저 설정해주겠습니다.
variables = {
'w1':1,'w2':2,'w3':3,'w4':4,'w5':5,'w6':6,'w7':7,'w8':8,
'b1':9,'b2':10,'b3':11,'b4':12,
'x1':13,'x2':14
}- 이어서 레이어에서 사용할 함수를 선언해줍니다.
def weight_sum(w1,w2,b1,x1,x2):
return w1*x1+w2*x2+b1
def summation(x1,x2):
return x1+2*x2- 이전 절에서 정의한 함수들과 동일하게 레이어들을 작성합니다.
layers = {
'f':{ # 레이어 이름
'func':weight_sum, # 사용할 함수
'inputs':['w1','w2','b1','x1','x2'], # 함수에 들어갈 입력
},
'g':{
'func':weight_sum,
'inputs':['w3','w4','b2','x1','x2'],
},
'h':{
'func':weight_sum,
'inputs':['w5','w6','b3','f','g'],
},
'i':{
'func':weight_sum,
'inputs':['w7','w8','b4','f','g'],
},
'j':{
'func':summation,
'inputs':['h','i'],
}
}- layers와 variables를 이용한 순전파 코드를 작성합니다.
forward_grads={}
def forward(name,eps=1e-10):
inputs = [variables[k] for k in layers[name]['inputs']] # 선택한 레이어의 입력 값을 variables에서 가져옴
out = layers[name]['func'](*inputs) # 레이어 실행
grad = {}
for i,k in enumerate(layers[name]['inputs']):
# 모든 변수에 대해서 목표로 하는 변수의 값만 값만 조절하여 편미분
inputs[i] = inputs[i]+eps
grad[k] = (layers[name]['func'](*inputs)-out)/eps
inputs[i] = inputs[i]-eps
variables[name] = out # 변수에 레이어 출력값 저장
forward_grads[name] = grad # 순전파 그래디언트 저장
return out- 전체 레이어에 대해 순전파를 진행합니다.
for name in layers.keys():
out = forward(name)
print(name,variables[name])
forward_grads- 역전파를 진행합니다.
backward_grads = {}
def backward(name,grad=1):
for i,k in enumerate(layers[name]['inputs']): #모든 레이어의 입력(이전노드)에 대해서 역전파 실행
if layers.get(k) is not None: # 레이어인 경우
backward(k,grad*forward_grads[name][k])
else : # 가중치인 경우
if backward_grads.get(k) is not None:
# 역전파된 기록이 있다면 더해주기
backward_grads[k] = backward_grads[k] + grad*forward_grads[name][k]
else :
# 역전파된 기록이 없다면 새로 선언
backward_grads[k] = grad*forward_grads[name][k]
backward('j') # 마지막 레이어에 대해 역전파를 진행.- 역전파가 잘 진행됐는지 확인합니다.
print(backward_grads['w1'])
print(variables['w5']*variables['x1']+2*variables['w7']*variables['x1'])
# 247.1311126871836
# 247학습 코드
def weight_sum(w1,w2,b1,x1,x2):
return w1*x1+w2*x2+b1
def summation(x1,x2):
return x1+2*x2
def mse(pred,true):
return (pred-true)**2
layers = {
# ... 이전코드와 동일
'loss':{
'func':mse,
'inputs':['j','y1'],
}
}
def forward(name,eps=1e-10):
# ... 이전 코드와 동일
return out
def backward(name,grad=1):
# ... 이전 코드와 동일
def update(params,lr=1e-3): # 가중치 업데이트 코드
for p in params:
variables[p] = variables[p]-lr*backward_grads[p]
variables = { # 변수들 정보 저장
# ... 이전 코드와 동일
}
params = [ # 학습될 파라미터 정보 저장
'w1','w2','w3','w4','w5','w6','w7','w8',
'b1','b2','b3','b4',
]
epochs=100
losses = []
forward_grads={}
for i in range(epochs):
loss = []
for j in range(100):
backward_grads = {} # backward 정보 삭제
variables['x1'],variables['x2'],variables['y1'] = j/100,j/100,j/100
for name in layers.keys(): # forward
out = forward(name)
backward('loss')
update(params)
loss.append(out)
losses.append(sum(loss)/100)
print(variables) # 변수들 값 확인
# 학습이 잘 됐는지 확인
variables['x1'],variables['x2'] = 1000,1000
for name in layers.keys(): # forward
out = forward(name)
print(variables['j'])
# 999.987289779996
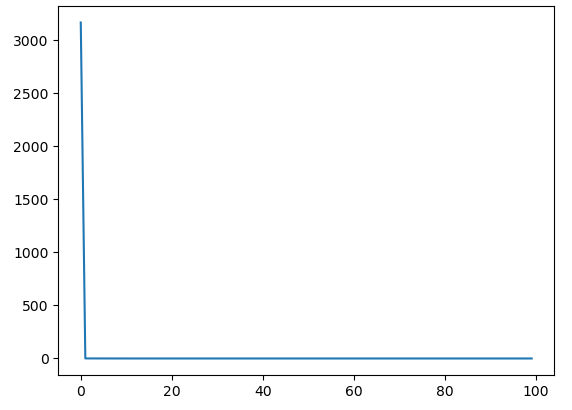
import matplotlib.pyplot as plt
plt.plot(losses)
plt.show()
마무리
'미분함수 정의' 방법의 문제점을 '미분 공식 활용' 방법의 문제점을 연쇄법칙을 통해 해결하는 과정을 보이며 순전파와 역전파에 대해서 설명 드렸습니다.
그러나 '미분공식과 연쇄법칙을 활용하는 방식' 에도 문제가 있습니다.
각 함수의 그래디언트를 구하기 위해서 모든 변수에 한번씩 변화를 주어 편미분 값을 계산하는 방식을 사용했습니다.
이 과정에서 변수의 개수만큼 함수를 여러번 실행해야하는 단점이 있습니다.
이 문제뿐만이 아니라 모델 구조를 새로 만들 때 입력 정보, 변수 정보, 함수 등 새로 명시해주어야 할 정보가 많은 문제점이 있습니다.
다음 글에서는 이런 문제점을 해결하기 위해 클래스 구조를 활용하여 구현하는 방식에 대해 글을 적으려고 합니다.
