[PyTorch] 가중치 고정

김태훈·2024년 5월 6일

Deep Learning PyTorch 실험

소개

인공지능 모델의 레이어의 가중치를 고정(Freeze 혹은 Lock) 하고자 할 때 자료를 찾아보면 requires_grad, no_grad(), detach() 등 여러가지 방법을 사용합니다.

셋의 차이점을 검색하면 차이점에 대해 얘기를 하지만 뭔가 확 와닿지는 않았습니다.

어떨 때, 무엇을, 왜 써야하는가?

가중치 고정, Grad 계산하지 않음, Graph... 등 여러 이유가 있음에도 설명이 모호한 경우가 많았습니다.

그래서 이를 명확히 정리하고자 하여 이 글을 작성합니다.

글을 읽기 전 아래의 글을 먼저 이해하고 오시는 것을 추천합니다.(양은 좀 많지만 이해하는데 도움이 될 수 있습니다.)

[딥러닝] 경사하강법 구현부터 학습까지 시리즈 : 경사하강법은 무엇이고 어떻게 모델을 학습시키는지에 대한 글
[PyTorch] AutoGrad란 무엇인가? 시리즈 : PyTorch에서는 순전파와 역전파를 어떻게 하는가에 대한 글

가중치 고정이란?

실험을 진행하기 위해 PyTorch나 Tensorflow 같은 딥러닝 프레임워크를 쓰면서 학습을 진행하다보면 특정 가중치를 학습에 참여하지 못하게 하고 싶은 경우가 많습니다.

대표적으로 사전학습된(Pre-Trained) 모델을 수정하고 미세조정(Fine-Tuning)하는 과정처럼 기존의 가중치가 이미 충분한 역할(특징 추출, 특징 합성 등)을 한다고 판단할 때입니다.

다음의 과정을 통해 가중치 고정을 간단하게 보이겠습니다.

다음과 같은 수식이 있다고 해봅시다.

x+2 = 3

1차적으로 계산을 통해 $x=1$ 임을 확신할 수 있습니다.

두번째 수식이 다음과 같이 주어진다고 하면

x+y=4

우리는 기존의 $x$ 를 바꾸지 않고 $y=3$ 인 것을 알 수 있습니다.

이를 인공지능 모델에 비유하면 다음과 같습니다.

$x$ 는 기존에 하나의 가중치로 이루어진 모델이며, $x=1$ 임을 알아가는 과정은 사전학습 과정이고, $x+y$ 는 두개의 가중치로 이루어진 수정된 모델 구조이고, $x=1$ 로 고정하여 미세조정하여 $y=3$ 인 것을 알아가는 과정

즉, 가중치 고정이란 인공지능을 학습하는 과정에서 특정 가중치가 정답에 가깝다고 판단하는 경우 학습과정에 인위적으로 개입하여 가중치가 업데이트 되지 않도록하는 것이라고 할 수 있습니다.

물론, 실제로 거대하고 복잡한 구조를 가진 모델 속에 있는 각 가중치들이 제대로 된 역할을 알기는 쉽지 않습니다.

그저 실험적으로 '1~4번째 레이어는 충분한 특징에 대해서 학습했구나' 정도만 알 수 있습니다.

그렇기 때문에 인공지능 모델의 성능을 향상시키고자 하는 경우 가중치 고정은 조심히 다루어야 합니다.

가중치 고정 장점

그렇다면 장점은 무엇이 있을까요?

사실 가중치 고정이라는 이론만으로는 장점을 찾아내기가 어렵습니다.

위에서 말한 것과 유사하게 변수를 줄여나가는 것도 장점이라고 하면 장점일 수도 있지만 변수가 수백만가지가 된다면 이 또한 의미가 없게 됩니다.

그러나 컴퓨팅 연산으로 접근을 하게된다면 연산량의 장점이 있습니다.

간단하게 보게 된다면, 100만개의 변수들을 업데이트 해야하는 경우에 절반을 고정하면 그중 절반의 연산만 하게 됩니다.

또한 경사하강법에서 가중치를 업데이트 하기 위한 Gradient 계산을 하지 않음으로써 연산량을 그만큼 줄일 수 있게 됩니다.

PyTorch Autograd

우선 PyTorch의 AutoGrad에 대해 간단하게 설명하고 넘어가겠습니다.

PyTorch는 기본적으로 연산에서 각 변수의 기울기를 자동으로 계산하도록 해주는 AutoGrad를 가지고 있습니다.

특정 연산의 정보와 연산에 사용한 변수들에 대한 정보를 연산 그래프(Computational Graph)로 저장하고 있습니다.

이렇게 순전파 과정에서 연산 그래프에 대한 정보를 가지고 있기 때문에 알 수 있고 이를 기반으로 역전파가 가능하게 됩니다.

연산 그래프 (Computational Graph)

그렇다면 연산 그래프가 무엇인지에 대해 이해해보겠습니다.

연산 그래프라고 해서 어떤 복잡한 자료구조가 사용된다고 생각하실 수도 있지만 그렇지 않습니다.

아래처럼 간단하게 연산 과정을 표처럼 표현한다고 보시면 됩니다.

※ PyTorch Autograd Explained - In-depth Tutorial에 과정이 정말 잘 설명되어 있습니다.

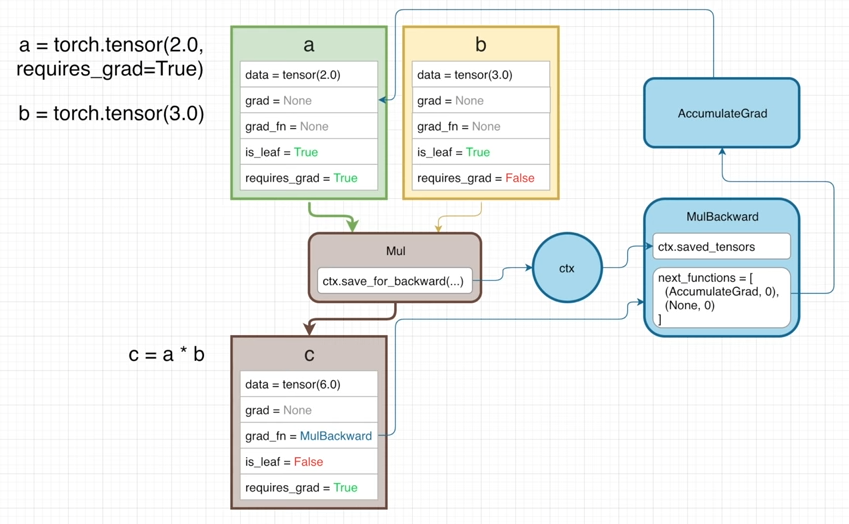
위 표는 $c = a \times b$ 에 대한 연산을 연산 그래프로 표현한 것입니다.

그럼 PyTorch에서는 이 연산 그래프를 어떻게 구성하는 것일까?

PyTorch에서는 연산 그래프에 대한 정보를 grad_fn을 통해 저장하고 있습니다.

grad_fn은 특정 Tensor가 생성될때 사용된 연산(사진 속 MulBackward)에 대한 정보와 입력(사진 속 ctx.saved_tensor)에 대한 정보가 담겨있습니다.

즉, 이전 노드(입력)에 대한 정보와 연산 정보를 가지고 있으므로 연산 그래프를 구성할 수 있게되고 그래프를 따라 역전파를 할 수 있게 됩니다.

가중치 고정 방법

PyTorch에서는 가중치 고정 방법은 여러가지가 있습니다.

대표적으로 no_grad(), requires_grad, detach(), Optimizer에 변수 등록 등이 있습니다.

이 네가지의 특징을 설명하면서 각각이 어떻게 작동하는지 보여드리겠습니다.

경사하강법

우선 가중치 고정 방법에 대해서 설명드리기 전 간단하게 경사하강법의 작동 원리를 설명 드리겠습니다.

경사하강법은 크게 3단계로 나뉘어 작동합니다.

순전파(Forward Propagation) 단계 : 각 레이어에서의 연산을 진행하며 연산에 대한 정보를 저장합니다.(연산 그래프 정의)
역전파(Back Propagation) 단계 : 저장된 연산정보를 통해 Gradient를 계산하여 역으로 전파하여 출력에 대한 각 가중치의 미분값을 계산합니다.
가중치 갱신(Weight Update) 단계 : 계산된 Gradient 값을 통해 각 가중치의 값을 갱신합니다.

가중치 고정은 각 단계 중 일부를 제어하면서 가중치를 고정합니다.

PyTorch에서 각 단계는 다음과 같이 구현됩니다.

import torch
import torch.nn as nn

# 함수 정의
def f(x):
    return x**2

# 파라미터 정의 
x = nn.Parameter(torch.rand(1))

# 옵티마이저 정의 : x라는 변수를 lr만큼 학습하겠다는 의미를 가집니다.
optimizer = torch.optim.SGD(params=[x],lr=0.1)

# 기존의 기울기 정보 초기화
optimizer.zero_grad()

# 순전파 : 주어진 함수(모델)에 맞게 연산을 진행함과 동시에 각 변수의 Gradient를 얻어냅니다.
out = f(x)

# 역전파 : 순전파를 통해 얻어낸 Gradient를 연쇄법칙을 이용해 각 파라미터의 기울기 값을 얻어냅니다.
out.backward()

# 갱신 : 선언할 때 입력받은 params의 기울기에 맞게 값을 변경합니다.
optimizer.step()

이제 위에서 언급한 각 방법이 어떤 단계를 어떻게 제어하는지 알아가면서 각각의 장단점을 확인해보겠습니다.

requires_grad

우선 requires_grad의 값을 변경하는 방식은 가장 흔히 사용되는 방식입니다.

특정 Tensor a의 requires_grad를 True로 설정하게 되면 이를 이용한 연산의 결과 Tensor에 대해서 requires_grad를 True로 설정하게 되며, requires_grad가 True이므로 grad_fn도 지정되게 됩니다.

즉, 특정 Tensor a와 연관된 모든 연산은 연산 그래프에 포함되게 됩니다.(연산 그래프의 예시 그림 참조)

그렇다면 여러 입력을 받는 연산(Add, Sub, Mul, Div 등)으로 인해 생긴 Tensor의 requires_grad는 어떻게 정해질까?

두 Tensor 중 하나라도 requires_grad가 True인 경우 결과 Tensor의 requires_grad는 True가 됩니다. (or 연산)

그렇다면 $c=a \times b$ 와 같은 연산을 할 때 각각의 requires_grad가 True, False면 역전파 과정에서 Tensor b에도 기울기가 저장되는 거 아니야?

물론 입력 Tensor a의 requires_grad가 True이기 때문에 결과 Tensor c의 requires_grad는 True로 grad_fn에는 MulBackward가 지정이 되긴 합니다.

하지만 grad_fn에서는 특정 입력의 requires_grad가 False인 경우에는 해당 노드에 대해서 Gradient를 전달하지 않습니다.

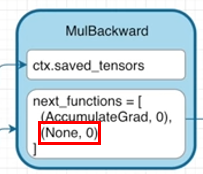
※ 여기서 next_functions 는 특정 입력에 어떻게 Gradient를 전달할지에 대한 정보가 담겨있습니다. (None이면 전달 하지 않음)

이렇기 때문에 역전파 단계에서 전달되는 Gradient가 없으므로 Tensor b의 grad는 None이 될 것이며 이 때문에 가중치 갱신 단계에서도 Tensor b의 가중치가 업데이트 되지 않습니다.

requires_grad의 값을 변경하는 과정은 순전파 단계부터 제어를 하여 가중치를 고정하는 방식입니다.

또한 특정 연산에 대해 입력 Tensor들의 requires_grad가 모두 False로 두게 된다면 다음과 같은 장점이 있습니다.

메모리 사용량 감소 : Gradient의 흐름이 필요가 없으므로 연산에 대한 정보, 입력에 대한 정보를 저장할 필요가 없어지게 됨
역전파 연산량 감소 : requires_grad가 False가 되고 grad_fn이 지정되지 않으면서 Gradient를 전달하지 못하게 되면서 불필요한 역전파가 사라지고 이에 따라 연산량이 감소하게 됩니다.

torch.no_grad()

no_grad() 방식은 다음과 같이 with문과 함께 사용됩니다.

with torch.no_grad():
	out = linear(x)
    out = activation(out)
    ...

requires_grad 여부에 관계 없이 해당 with 문 안에서의 모든 연산에 대해서 requires_grad를 False라고 간주하고 연산하게 됩니다.

$c= a \times b$ 에 대한 결과를 보이기 위해 다음과 같은 예시 코드를 작성할 수 있습니다.

import torch

a = torch.tensor([1.], requires_grad=True)
b = torch.tensor([1.], requires_grad=True)

with torch.no_grad():
    c = a*b

d = a*b

print(c.grad_fn, c.requires_grad)
#> None False
print(d.grad_fn, d.requires_grad)
#> <MulBackward0 object at 0x0000018998D6AD60> True

Tensor a, b 모두 requires_grad를 False로 간주하기 때문에 그 결과로 생성되는 Tensor는 requires_grad는 False이며 grad_fn은 None이 되게 됩니다.

위 방식이 이전 방식에 비해 좋은 점은 간단하고 쉽게 Gradient의 흐름을 제어할 수는 있지만 모델이 복잡해지는 경우 Tensor a, b에 의도치 않게 Gradient를 흐르게 하여 가중치가 고정되지 않을 수 있습니다.(Tensor d에 역전파가 되는 경우)

detach()

requires_grad 방식과 torch.no_grad 방식은 연산을 진행하는 과정에서 연산 그래프를 제어하게 됩니다.

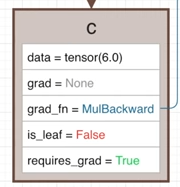
즉, Tensor a, b의 연산 중에 결과 Tenscor c의 requires_grad와 grad_fn이 정해집니다.

그러나 detach는 연산이 완료되고 난 후의 시점에서 연산그래프를 제어합니다.

아래의 코드를 통해 살펴보면 다음과 같습니다.

import torch

a = torch.tensor([1.], requires_grad=True)
b = torch.tensor([1.], requires_grad=True)

c = a*b

print(c.grad_fn, c.requires_grad)
#> <MulBackward0 object at 0x00000189A63B7DF0> True

d = c.detach()

print(c.grad_fn, c.requires_grad)
#><MulBackward0 object at 0x00000189A63B7DF0> True
print(d.grad_fn, d.requires_grad)
#>None False

물론 replace 연산이 아니기 때문에 Tensor c에 바로 적용되지는 않지만 이전의 방식들과는 달리 c가 생성된 이후에 detach()를 적용하여 연산그래프에서 제외시킵니다.(replace 연산으로 하려면 detach_() 사용)

위 방식은 no_grad 방식과 유사한 특징을 가지고 있지만, 이전 방식들과는 달리 연산 후에 연산 그래프에서 제외하는 방식이기 때문에 연산량과 메모리에 대한 장점이 사라지게 됩니다.

Optimizer에 변수 등록

이전까지의 방법들은 순전파 과정에서 연산그래프를 제어하여 Gradient의 흐름을 제어하여 가중치를 고정하였습니다.

Optimizer에 변수를 등록하는 방식은 가중치 갱신 과정에서 변수들의 정보를 제어하여 가중치를 고정하는 방식입니다.

PyTorch에서 Optimizer의 역할은 계산된 Gradient를 기반으로 가중치를 갱신하는 역할을 하게 됩니다.

기존의 학습 코드를 다시 가져와서 살펴보며 설명하겠습니다.

import torch
import torch.nn as nn

# 함수 정의
def f(x):
    return x**2

# 파라미터 정의 
x = nn.Parameter(torch.rand(1))

# 옵티마이저 정의 : x라는 변수를 lr만큼 학습하겠다는 의미를 가집니다.
optimizer = torch.optim.SGD(params=[x],lr=0.1)

# 기존의 기울기 정보 초기화
optimizer.zero_grad()

# 순전파 : 주어진 함수(모델)에 맞게 연산을 진행함과 동시에 각 변수의 Gradient를 얻어냅니다.
out = f(x)

# 역전파 : 순전파를 통해 얻어낸 Gradient를 연쇄법칙을 이용해 각 파라미터의 기울기 값을 얻어냅니다.
out.backward()

# 갱신 : 선언할 때 입력받은 params의 기울기에 맞게 값을 변경합니다.
optimizer.step()

보시는 것처럼 Optimizer는 선언됨과 동시에 params 변수에 학습시키고자하는 파라미터에 대한 정보를 받습니다.

zero_grad()는 params 변수에 있는 파라미터들에 지금까지 저장된 Gradient 값을 0으로 초기화 하는 역할을 하고, step()은 지금까지 저장된 Gradient 값을 기반으로 파라미터 값을 변경하게 됩니다.

즉, params로 주어지지 않은 변수에 대해서는 가중치를 갱신하지 않게됩니다.

가령 Tensor a, b가 있다고 할 때 Optimizer의 params에 a에 대한 정보만 제공하는 경우를 살펴보겠습니다.

import torch

a = torch.tensor([1.], requires_grad=True)
b = torch.tensor([1.], requires_grad=True)

optimizer = torch.optim.SGD(params=[a],lr=0.1)

optimizer.zero_grad()

c = a * b

print(a.data, a.grad, a.grad_fn, a.requires_grad)
#> tensor([1.]) None None True
print(b.data, b.grad, b.grad_fn, b.requires_grad)
#> tensor([1.]) None None True
print(c.data, c.grad, c.grad_fn, c.requires_grad)
#> tensor([1.]) None <MulBackward0 object at 0x00000252C7D07190> True

c.backward()

print(a.data, a.grad, a.grad_fn, a.requires_grad)
#> tensor([1.]) tensor([1.]) None True
print(b.data, b.grad, b.grad_fn, b.requires_grad)
#> tensor([1.]) tensor([1.]) None True
print(c.data, c.grad, c.grad_fn, c.requires_grad)
#> tensor([1.]) None <MulBackward0 object at 0x00000252C7D07B80> True

optimizer.step()

print(a.data, a.grad, a.grad_fn, a.requires_grad)
#> tensor([0.9000]) tensor([1.]) None True
print(b.data, b.grad, b.grad_fn, b.requires_grad)
#> tensor([1.]) tensor([1.]) None True
print(c.data, c.grad, c.grad_fn, c.requires_grad)
#> tensor([1.]) None <MulBackward0 object at 0x00000252C7D07FD0> True

※ optimizer.zero_grad()를 해야하는 이유는 step() 이후의 결과를 확인해보면 Tensor a, b의 grad가 유지되는 것을 확인할 수 있으며 다음 backward()를 실행한다면 새로운 Gradient가 grad에 계속 축적되게 됩니다.

우선 결과부터 살펴본다면 Tensor a의 값은 1.0 에서 0.9000으로 변경이 되었지만 Tensor b의 값은 1.0에서 변하지 않은 것을 확인할 수 있습니다.

분명 Tensor a, b 모두 requires_grad가 True이고 c.backward() 이후에 정상적으로 Gradient가 역전파 되었는데 왜 갱신이 되지 않았지?

그 이유는 Optimizer의 params 변수에 Tensor b를 입력하지 않았기 때문에 Optimizer는 Tensor a의 값만 변경하게 됩니다.

즉, Tensor b의 requires_grad를 False로 둔 결과와 동일하게 나오게 됩니다.

하지만 requires_grad가 모두 True로 되어 있기 때문에 불필요한 연산그래프가 발생하게 되며 이 때문에 requires_grad 방식에 비해 연산량, 메모리 사용량 감소의 장점이 사라질 수 있습니다.

※ step() 과정에서 파라미터 수가 줄어듦에 따라 연산량 감소하는 효과는 있지만 크게 감소하지는 않음

마무리

이번 글에서는 가중치 고정을 위한 주요 방법 4가지와 그 원리에 대해서 설명하였습니다.

4가지 방법 모두 다른 특성을 가지고 있어 구조를 설계하는 과정에서 적절한 방법을 사용하면 될 거 같습니다.

저는 안전하게 고정하고자 하는 파라미터의 requires_grad를 False로 시켜두고 Optimizer의 params에 제외시키는 방식을 사용하고 있습니다.

다시 한 번 글에서 보여드린 예시코드를 기반으로 모델을 더 깊고 복잡하게 쌓으면서 중간중간 결과도 확인하시면서 익숙해지시면 나중에 Fine-Tuning처럼 가중치를 고정해야할 때 쉽게 하실 수 있으실 겁니다.

김태훈

👋 인공지능을 통해 다음 세대가 더 나은 삶을 살도록

이전 포스트

[PyTorch] AutoGrad란 무엇인가? (2)

다음 포스트