배경
딥러닝에서 ResNet, MobileNet 등 여러 모델에서 Bottleneck 구조를 사용합니다.
왜 Bottleneck 구조를 사용할까?
위에 대한 질문에서 Bottleneck은 다음과 같은 역할을 한다고 생각합니다.
-
채널을 줄이며 이후 이어질 레이어에 대한 연산량 감소
-
비선형성 증가(추가된 레이어에 비선형 함수가 추가되는 경우)
-
좁아진 채널에 의한 중요한 특징 추출
-
중복을 줄인 효율적인 특징 추출
1번과 2번은 너무도 잘 알려진 사실이고 쉽게 이해할 수 있지만 3번과 4번은 자주 들어본 말은 아닐 것입니다.
이번 글은 이 3번과 4번을 시각화 할 수 있도록 PyTorch를 통해 간단한 실험을 할 예정입니다.
근거
3번 4번에 대한 생각을 가진 근거는 다음과 같습니다.
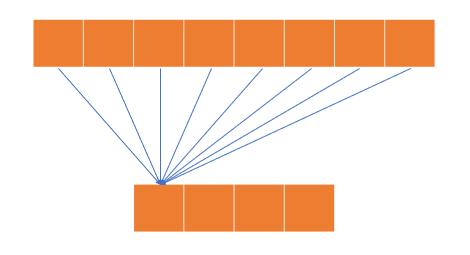
위와 같은 레이어 이외의 다른 레이어는 없다고 가정합니다.
처음에는 8개의 특징들이 있지만 이 특징들을 4개의 특징으로 압축해야하고 몇몇 특징들을 적게 가져오거나 버려야 하기 때문에 정보의 손실이 발생합니다.
모델은 주어진 데이터에 맞는 최적의 값으로 각 가중치를 학습시켜 특징들을 추출할 것입니다.
즉, 정보를 버릴 수 밖에 없는 상황이라면 모델은 주어진 데이터를 잘 설명할 수 있는 특징(최적의 특징)들만 최대한 남기려고 할 것입니다.
이러한 근거로 3번에 대한 생각으로 이어졌습니다.
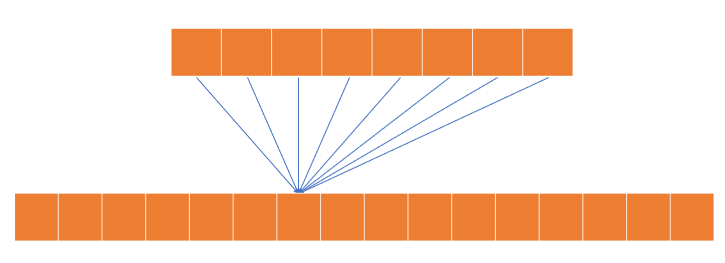
반대로 위와 같이 채널의 수가 많아지는 상황이라고 한다면 기존의 특징들을 조합해 더 많은 특징을 추출할 수 있게 됩니다.
채널의 수가 많아지면 더 많은 특징을 추출할 수 있어서 좋을 수는 있으나 연산량이나 메모리 관점에서 비효율적일 수 있습니다.
특히 블록 내의 두 특징이 가중치가 비슷한 경우가 발생할 수 있고 이를 중복된 특징이라고 합니다.
중복된 특징이 많아진다는 것은 결국 비효율적으로 특징을 추출했다는 것이라고 생각합니다.
이러한 근거로 4번에 대한 생각으로 이어졌습니다.
실험 환경
3번 4번 내용에 대한 간단한 실험을 할 예정입니다.
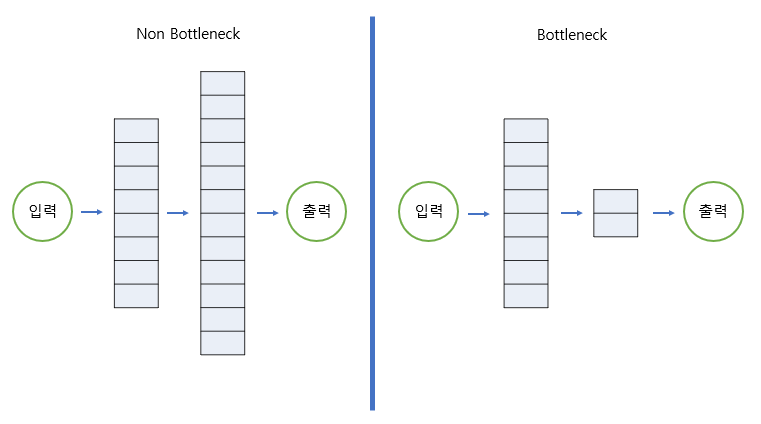
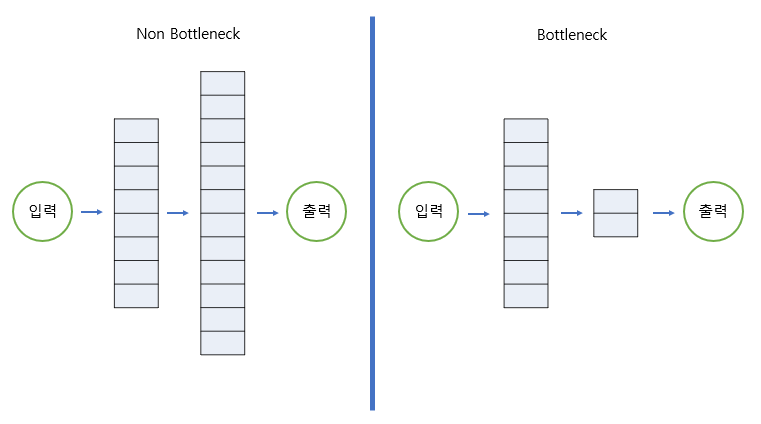
실험을 할 모델 구조는 다음과 같습니다.
간단한 숫자를 입력으로 하여 그대로 출력하도록 하는 매우 간단한 모델입니다.
모델 학습에 대한 데이터와 Hyper Paramater는 다음과 같습니다.
- 입력 데이터 : [0, 99] 범위의 정수
- 출력 데이터 : [0, 99] 범위의 정수
- Optimizer : Adam
- Lerning Rate : 1e-3
- Epoch : 100
- Loss : Mean Square Error
실험 과정은 다음과 같습니다.
-
초기 모델의 각 레이어(입력,레이어1,레이어2,출력)의 채널 수를(1,32,32,1)로 지정 하고 위의 설정으로 학습합니다.
-
레이어 1에 대한 변경 없이 레이어 2의 채널 수를 각각 8(Bottleneck)와 128(Non Bottleneck)으로 설정하여 주어진 설정으로 다시 학습합니다.
-
레이어 2에서 서로다른 두 가중치의 차이를 구하여 차이가 제일 작은 두개의 가중치를 출력한다.
-
3의 결과를 통해 중복된 가중치를 확인함과 동시에 최종 성능에 큰 차이가 있는지 확인한다.
실험코드
1. 모델 초기화, 데이터 초기화
# 라이브러리
import torch
import torch.nn as nn
import numpy as np
import random
# 데이터 초기화
sz = 100
input = torch.tensor(list(range(sz)),dtype=torch.float32).reshape(sz,1)
output = torch.tensor(list(range(sz)),dtype=torch.float32).reshape(sz,1)
original_channels = 32
# 모델 작성
class mymodel(nn.Module):
def __init__(self):
super(mymodel,self).__init__()
self.linear = nn.Linear(1,original_channels)
self.linear2 = nn.Linear(original_channels,original_channels)
self.out = nn.Linear(original_channels,1)
def forward(self,x):
out1 = self.linear(x)
out2 = self.linear2(out1)
out3 = self.out(out2)
return out1,out2,out3
2. 모델 학습 함수 작성
def train(epoch,bottleneck):
#Linear2 파라미터 초기화 Randomness 제거
model.linear2 = nn.Linear(original_channels,bottleneck)
model.out = nn.Linear(bottleneck,1)
optim = torch.optim.Adam(model.parameters(),1e-3)
for i in range(epoch):
optim.zero_grad()
out1,out2,out3 = model(input)
criterion = nn.MSELoss()
loss = criterion(out3,output)
loss.backward()
optim.step()
#마지막 학습 전 loss 출력
print(loss)
with torch.no_grad():
#비슷한 가중치 찾아내서 출력
min = 1000000
mini = 0
minj = 0
for i in range(bottleneck):
for j in range(i+1,bottleneck):
sub = torch.sum(torch.abs(model.linear2.weight[i]-model.linear2.weight[j]))/original_channels
if (sub<=min):
mini=i
minj=j
min = sub
print(model.linear2.weight[mini])
print(model.linear2.weight[minj])
print(min)3. 실험 진행 코드
compare_channel_list = [original_channels//4,original_channels,original_channels*4]
epoch = 100
for bottleneck in compare_channel_list:
#각 실험별 Seed 고정
seed = 10000
deterministic = True
random.seed(seed)
np.random.seed(seed)
torch.manual_seed(seed)
torch.cuda.manual_seed_all(seed)
if deterministic:
torch.backends.cudnn.deterministic = True
torch.backends.cudnn.benchmark = False
# 모델 선언
model = mymodel()
# Unfreeze
for i in model.parameters():
i.requires_grad=True
model = mymodel()
# Bottleneck 학습
print(f"\nBottleneck : {bottleneck}")
train(epoch,bottleneck=bottleneck)
print()결과
모든 코드 실행시 출력은 아래에 나와있습니다.
최종적인 결론은 다음과 같습니다.
-
본 실험 그대로 할 경우 Loss의 차이는 크게 없는 것으로 보이며 비슷한 두 가중치의 유사도가 Bottleneck > Original > Non Bottleneck임을 확인할 수 있습니다.
-
데이터가 적고 간단하기에 약간의 Hyper Paramater 변화에도 성능에 큰 차이를 일으킨다는 점이 있습니다.
-
여러 Hyper Paramater로 실험하더라도 유사도에 대한 결과는 항상 비슷하게 나왔습니다.
Original
Bottleneck : 32
tensor(0.0327, grad_fn=<MseLossBackward0>)
tensor([-0.1005, -0.0892, 0.0406, 0.1634, -0.0930, -0.0646, -0.0296, 0.0730,
0.0956, -0.0660, 0.0227, -0.1237, -0.0440, -0.0545, -0.1033, -0.0948,
-0.0555, -0.0421, 0.0174, 0.0411, -0.0317, -0.1123, -0.0312, -0.0024,
0.0306, 0.0440, -0.1417, 0.0863, -0.1388, 0.0147, 0.0610, 0.1370],
requires_grad=True)
tensor([ 0.0328, 0.0493, -0.1636, -0.0456, -0.0965, -0.0486, -0.0233, 0.0164,
0.0632, -0.0133, 0.1040, -0.0665, -0.0449, -0.1542, -0.0833, 0.1915,
-0.0613, 0.1244, -0.0450, 0.0476, -0.1852, -0.1056, 0.1859, -0.0685,
-0.1257, 0.0430, -0.0490, 0.0883, -0.0847, -0.0327, 0.0477, 0.0384],
requires_grad=True)
tensor(0.0796)Bottleneck
Bottleneck : 8
tensor(0.0354, grad_fn=<MseLossBackward0>)
tensor([-0.0092, -0.0476, -0.0979, 0.0840, 0.0314, 0.0732, -0.0192, -0.0119,
0.1228, 0.1942, 0.1335, 0.1377, 0.0784, -0.0794, -0.1055, 0.0812,
0.2063, -0.0891, 0.0041, 0.1664, 0.0559, 0.0270, -0.1117, -0.1162,
0.0452, -0.0664, 0.0555, 0.0897, -0.1405, 0.1602, 0.1077, -0.2005],
requires_grad=True)
tensor([ 0.0025, 0.1422, 0.1027, 0.0229, -0.0285, 0.1808, -0.1276, 0.0699,
0.1532, 0.1905, -0.0721, 0.1933, -0.1822, 0.0881, -0.1045, 0.0837,
0.0391, -0.0030, 0.0688, -0.0794, -0.0162, 0.0293, -0.1803, -0.1033,
-0.2029, -0.0846, 0.1163, -0.0197, -0.1709, 0.1865, 0.0993, -0.1084],
requires_grad=True)
tensor(0.0894)
Non Bottleneck
Bottleneck : 128
tensor(0.0337, grad_fn=<MseLossBackward0>)
tensor([ 0.0780, -0.1490, -0.1028, -0.0582, 0.0137, 0.1581, 0.0408, -0.1516,
0.0989, 0.1572, -0.0914, -0.0469, 0.1070, 0.1179, -0.0554, -0.1081,
0.0397, -0.0492, -0.0518, -0.0335, 0.0180, 0.0886, -0.0080, 0.0429,
0.0058, 0.0606, 0.0514, -0.1043, 0.1415, -0.1502, -0.1582, -0.0168],
requires_grad=True)
tensor([ 0.1208, -0.0554, -0.1297, -0.0882, -0.0025, 0.1689, -0.0483, -0.1753,
0.0915, -0.0550, -0.0595, -0.1108, -0.0713, 0.1125, -0.0311, -0.1130,
-0.0325, -0.0082, -0.0183, -0.1631, 0.0311, 0.0136, 0.1174, -0.0964,
0.0824, 0.1570, 0.0624, -0.1177, 0.1512, -0.1024, 0.1574, -0.0709],
requires_grad=True)
tensor(0.0661)참고