🧠 데이터 구조와 처리: 컴퓨터가 데이터를 '잘' 쓰는 법

📍 왜 '데이터 구조'를 알아야 할까?

컴퓨터 구조를 공부하면서 자연스럽게 자주 등장하는 주제가 있습니다. 바로 '메모리'.

3장에서는 DRAM, 플래시, 디스크 드라이브의 접근 속도 차이를, 5장에서는 캐시 메모리에 데이터가 있는지 여부가 얼마나 성능에 큰 차이를 내는지에 대해 배웠죠.

참고 자료 : 캐시 메모리 성능

캐시 메모리의 존재 여부는 프로그램 성능에 지대한 영향을 미칩니다. 캐시 히트(cache hit)와 캐시 미스(cache miss)의 차이는 메모리 접근 속도에서 큰 차이를 만들어냅니다.

캐시 계층별 접근 시간 예시

다음은 일반적인 캐시 계층 구조에서 각 계층의 접근 시간과 캐시 미스 발생 시의 지연 시간을 나타낸 표입니다

계층	접근 시간 (ns)	캐시 미스 발생 시 추가 지연 시간 (ns)
L1 캐시	1	5 (L2 접근 시간)
L2 캐시	5	10 (L3 접근 시간)
L3 캐시	10	50 (메인 메모리 접근 시간)
메인 메모리	50	-

예를 들어, L1 캐시에서 데이터가 존재하면 1ns 만에 접근이 가능하지만, 캐시 미스가 발생하여 메인 메모리까지 접근해야 한다면 총 66ns(1 + 5 + 10 + 50)의 시간이 소요됩니다.

평균 메모리 접근 시간(AMAT)

평균 메모리 접근 시간은 다음과 같이 계산됩니다:

AMAT = 캐시 히트 시간 + (캐시 미스율 × 캐시 미스 패널티)

예를 들어, L1 캐시의 히트 시간이 1ns이고, 미스율이 10%, 미스 패널티가 50ns라면:

AMAT = 1 + (0.1 × 50) = 6ns

이러한 계산을 통해 캐시의 효율성을 평가하고, 시스템의 전반적인 성능을 예측할 수 있습니다.

캐시 미스의 영향

캐시 미스는 프로그램의 실행 속도를 현저히 저하시킬 수 있습니다. 따라서, 캐시 미스를 최소화하기 위한 전략이 중요합니다. 이러한 전략에는 데이터 지역성(locality of reference)을 고려한 알고리즘 설계, 적절한 캐시 크기 및 계층 구조 설정 등이 포함됩니다.

더 자세한 내용은 Wikipedia의 캐시 계층 구조에서 확인하실 수 있습니다.

이처럼 하드웨어가 빠른 컴퓨팅을 위해 끊임없이 최적화를 고민하고 있는 것처럼, 소프트웨어도 데이터를 어떻게 '잘' 저장하고, 불러오고, 수정하고, 없앨지 고민해야 합니다.

그래서 이 장에서는 바로 그 핵심! 데이터 구조를 이야기합니다.

즉, 데이터를 조직화하는 표준적인 방법을 살펴봅니다!

데이터 구조 중 상당수는 여러 유형의 메모리를 더 효율적으로 사용하기 위해 존재합니다. 어떤 연산을 더 빨리 작동하게 개선하려면 공간/시간 트레이드 오프가 발생하는 경우가 자주 있어요.

컴퓨터 하드웨어가 아니라 프로그래밍 언어가 고수준 데이터 구조를 지원한다는 사실을
알아둡시다.

1. 참조 지역성: '가까운 것'을 좋아하는 컴퓨터의 습성

지역성을 보기 전 기억장치들, 그림을 알면 좋은 것들

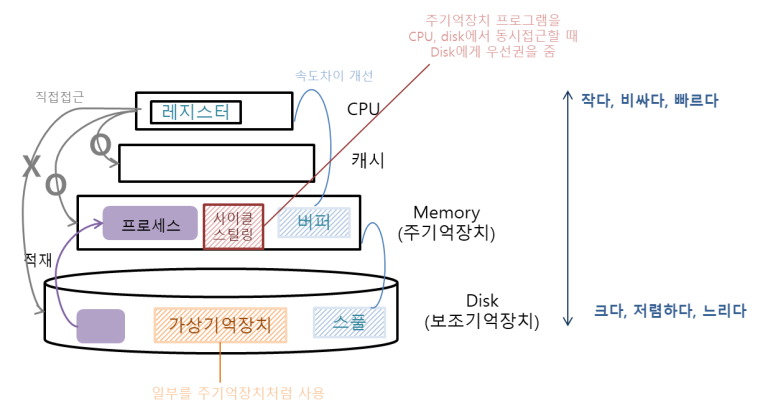
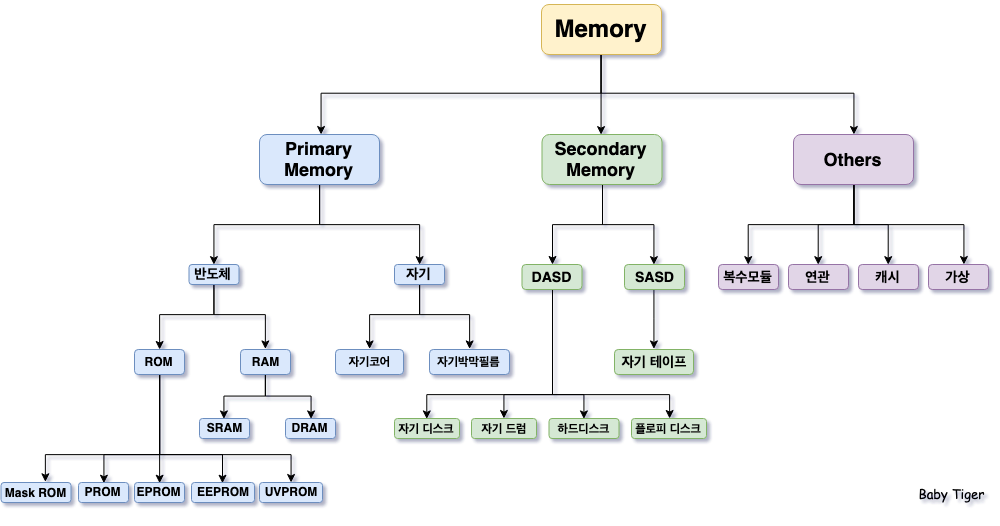
메모리 구조

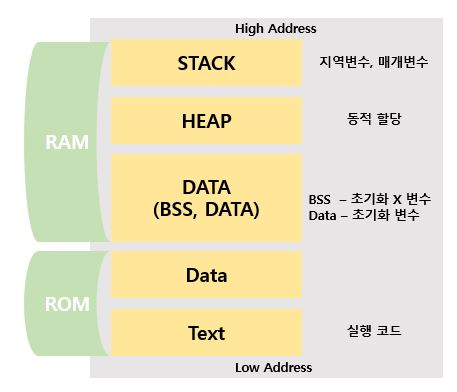
지역성이란?

컴퓨터에서 메모리에 접근하는 방식은 절대 무작위가 아닙니다. 오히려 컴퓨터는 우리가 생각하는 것보다 꽤나 예측 가능한 행동을 하곤 하죠. 이 예측 가능한 패턴을 정리한 개념이 바로 참조 지역성(Reference Locality)입니다.

🔎 왜 메모리 계층 구조는 "가성비"가 좋은 걸까?

현대 컴퓨터는 빠르고 비싼 메모리(L1 캐시)부터 느리지만 저렴하고 용량이 큰 저장소(SSD/HDD)까지 다양한 메모리 계층 구조를 사용합니다.
그런데, 이렇게 작은 용량의 캐시를 두는 것만으로도 체감 성능이 확 좋아진다면?
그 비밀은 바로 소프트웨어와 프로그래밍 습관에서 비롯되는 지역성(Locality) 덕분입니다

1️⃣ 참조 지역성의 핵심 정의

“필요한 데이터는 가까이에 있다. 방금 쓴 데이터는 또 쓴다.”
바로 이 말이 참조 지역성(Locality of Reference)을 설명하는 핵심 문장입니다.

컴퓨터는 특정 데이터를 한 번 참조한 후, 짧은 시간 안에 다시 참조하거나, 그 데이터 근처의 메모리를 참조할 가능성이 높다는 원칙에 따라 동작합니다.

컴퓨터는 필요한 데이터를 메모리에서 서로 가까운 곳에 두면 더 빠르게 접근할 수 있습니다. 이를 "참조 지역성(locality of reference)"이라고 합니다.

예를 들어볼게요.

냉장고를 생각해봅시다. 자주 꺼내 먹는 김치나 달걀은 문 쪽에 두는 게 편하겠죠? 자주 먹는 것들을 가까이 두는 것, 이게 바로 참조 지역성입니다.

컴퓨터 과학에서 참조 지역성(Reference Locality; 지역성의 원리)은 프로세서가 짧은 시간 동안 반복적으로 동일한 메모리 위치 집합에 액세스하는 것입니다.

참고 : https://velog.io/@seony-dev/%ED%94%84%EB%A1%9C%EA%B7%B8%EB%9E%98%EB%B0%8D-07.-%EB%A9%94%EB%AA%A8%EB%A6%AC-%EC%A7%80%EC%97%AD%EC%84%B1Locality-of-reference

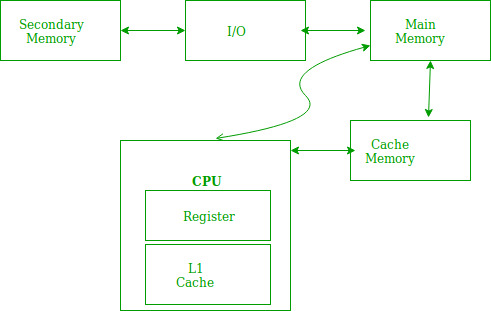
지역성은 컴퓨터 시스템에서 발생하는 예측 가능한 동작 유형이에요. 참조 지역성이 강한 시스템은 성능 최적화를 위해 캐싱, 메모리 프리페칭, 고급 분기 예측기 등의 기술을 활용합니다.

CPU가 메모리에 접근할 때의 주된 경향을 바탕으로 만들어진 원리이자, 캐시 메모리가 메모리로부터 가져올 데이터를 결정하는데에 쓰이는 원칙입니다.

🔍 참조 지역성의 종류

1) 시간적 지역성 (Temporal Locality)

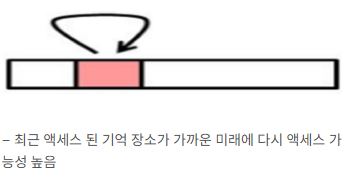
• “방금 사용한 데이터를 또 사용할 확률이 높다”
• CPU는 최근에 접근했던 메모리 공간에 다시 접근하려는 경향이 있음
• 예시: 반복문 내에서 같은 변수 참조하기 (for 루프의 i)
• 예시2 : 서브 루틴, 공통 변수, LRU

CPU가 변수에 값을 저장하고 나면 언제든 변수에 다시 접근이 가능한데, 변수는 일반적으로 한 번만 사용되지 않고 여러 번 사용되며 변수는 메모리 공간에 저장되므로 이는 CPU가 최근에 접근한 변수가 저장된 메모리 공간을 여러 번 다시 접근할 수 있음을 의미

2) 공간적 지역성 (Spatial Locality)

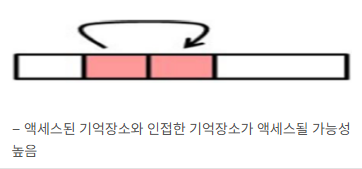
• “한 번 사용된 데이터 근처에 있는 데이터를 사용할 확률이 높다”
• 예시: 배열을 순차적으로 탐색할 때 인접한 메모리 접근
• CPU가 실행하려는 프로그램은 보통 관련 데이터들끼리 한 군데에 모여 있기 때문에 프로그램 실행 시 그 프로그램과 관련된 공간을 집중적으로 접근하게 됨

3) 분기 지역성 (Branch Locality)

• “조건문 혹은 루프 내에서 특정 분기문을 자주 타는 경우”
• 예시: if 문 안에 있는 특정 분기만 반복적으로 실행되는 경우

4) 등거리 지역성 (Equidistant Locality)

• “일정한 간격으로 데이터에 접근하는 경우”
• 예시: for (int i = 0; i < n; i += 3)처럼 일정한 스텝으로 배열 접근

💡 왜 이런 지역성이 생길까?

프로그래머의 습관 때문입니다.

• 대부분의 프로그램은 함수를 호출하면 그 안에서 같은 변수들을 계속 사용합니다.
  → 시간 지역성
• 배열이나 리스트는 순차적으로 탐색하는 경우가 많습니다.
  → 공간 지역성
• 조건문과 반복문이 자주 사용되며, 코드 실행 흐름도 반복되죠.
  → 시간 + 공간 지역성 동시 만족

💡 왜 이 개념이 중요할까?

✅ 캐시 성능 향상

“캐시가 데이터를 미리 준비할 수 있는 이유!”

• CPU는 L1 → L2 → L3 → 메인 메모리 순으로 메모리에 접근합니다.
• 최근에 참조된 데이터 혹은 그 주변 데이터를 미리 캐시해놓으면 빠른 연산이 가능하죠.
• 지역성이 높을수록 캐시 적중률(Cache Hit Rate)이 높아지고, 이는 곧 프로그램 성능 향상으로 이어집니다.

메모리 단계	접근 속도(ns)	비고
레지스터	1	가장 빠름
L1 캐시	2~4	매우 빠름
L2 캐시	10~20	빠름
L3 캐시	30~60	보통
DRAM(메인 메모리)	100~200	느림
SSD/HDD	100,000~10,000,000	매우 느림

※ 위 표는 참고용이며, CPU와 시스템 아키텍처에 따라 다릅니다.

✅ 메모리 계층 최적화

• 하드웨어는 이 지역성을 활용하기 위해 여러 가지 계층 구조를 만듭니다.
• 대표적인 예시: 캐시, TLB(Translation Lookaside Buffer), 프리페치(Prefetch), 분기 예측기 등

✅ 소프트웨어 최적화에도 활용

• 데이터 구조 설계, 배열 순회 방식, 함수 호출 순서 조정 등
• 예: 배열 순회 시 행 우선(row-major)으로 데이터를 배치하면 캐시 적중률이 높아짐

🔧 어떻게 활용할 수 있을까?

1. 소프트웨어 측면 최적화

• 데이터를 배열이나 구조체에 인접하게 배치
• 최근에 접근한 데이터를 우선 사용하도록 루프 구조 설계
• 배열을 행 순서로 순회하도록 구현 (C언어 등은 row-major 방식)

2. 하드웨어 측면 활용

• 계층적 메모리 설계: 레지스터 - 캐시 - 메인 메모리 - SSD/HDD
• 캐시 라인(prefetch line)에 한 번에 여러 바이트를 불러오는 이유도 공간 지역성 때문
• 분기 예측기: 분기 지역성을 활용하여 잘 쓰는 루트를 빠르게 실행

📦 예시로 보는 참조 지역성

1. 시간적 지역성 예시

for (int i = 0; i < 1000; i++) {
    sum += array[i];
}

• array[i]는 바로 다음 루프에서 다시 참조되므로 시간적 지역성이 발생합니다.

2. 공간적 지역성 예시

for (int i = 0; i < 1000; i++) {
    process(array[i]); // 인접한 메모리 접근
}

• array[i], array[i+1], array[i+2]는 물리적으로 인접하므로 캐시로 묶어서 불러올 수 있음

📘 부가적으로 알면 좋은 개념들

✔️ 캐시 오염(Cache Pollution)

• 참조 지역성이 약한 데이터를 캐시에 자주 넣으면 쓸데없는 데이터로 캐시가 채워져 성능 저하 발생

✔️ 캐시 우회(Cache Bypass)

• 캐시가 낭비되지 않도록, 지역성이 낮은 데이터는 아예 캐시에 넣지 않는 방식도 존재 (DMA, non-temporal memory access)

✔️ 메모리 정렬(Alignment)

• 구조체의 각 필드를 잘 정렬해서 메모리 낭비를 줄이고, 캐시 적중률을 높이는 기법

⚙️ 지역성에 최적화된 캐시 메모리

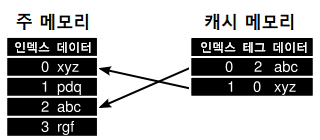
동적 CPU 메모리 캐시 그림 출처 : https://chelseashin.tistory.com/43

작은 캐시 메모리가 놀라운 성능 향상을 제공하는 이유는, 바로 이 지역성 원칙에 최적화되어 있기 때문입니다.

예를 들어,

• 최근에 사용한 데이터를 다시 쓰는 시간 지역성 덕분에 캐시에 있는 데이터를 재활용할 수 있고,
• 공간 지역성 덕분에 캐시 라인 하나만 불러와도 근처 데이터까지 같이 사용할 수 있게 됩니다.

✅ Locality 활용 사례 정리

구분	사례	설명	지역성 유형
1. Cache Memory	LRU (Least Recently Used)	- 캐시 교체 알고리즘 구현 - 참조 시간 기준 교체 블록 선정 - 가장 오랫동안 미사용 블록 교체	시간적, 공간적
	선인출 (Pre-Fetch)	- 캐시 인출 알고리즘 구현 - 향후 필요 예측 정보를 미리 캐시로 인출하여 배치	시간적, 공간적
2. Virtual Memory	워킹셋 (Working Set)	- Thrashing 해결 기법 - 특정 시간 실행 프로그램의 최근 참조 페이지 집합 구성	시간적
3. Network	CDN (Content Delivery Network)	- 콘텐츠를 효율적으로 전달하기 위해 여러 노드에 데이터를 분산 저장 - 사용자와 가까운 서버에서 콘텐츠 제공	공간적

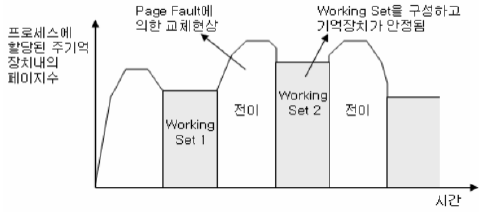
• working set

• CDN

🧭 LRU Cache 스케줄링 알고리즘

🔄 LRU (Least Recently Used) 알고리즘이란?

“가장 오랫동안 사용되지 않은 데이터를 캐시에서 제거하자.”

왜 필요할까?

캐시의 공간은 한정되어 있으므로, 새로운 데이터를 가져오려면 기존 데이터를 버려야 합니다. 그때 무작위로 버릴 순 없으니, 가장 덜 쓴 데이터를 제거하는 것이 합리적이겠죠.

예시:

• 최근에 접근한 데이터: A, B, C
• 새로운 데이터 D가 들어와야 할 때 캐시가 꽉 차 있다면?
  → 가장 오래된 A를 제거하고 D를 넣습니다.

장점:

• 시간 지역성을 기반으로 하여, 실제 사용 패턴에 잘 맞음
• CPU 캐시, 웹 브라우저 캐시 등 다양한 곳에서 활용됨

단점:

• LRU를 정확히 구현하려면 최근 사용 시점을 추적해야 하므로 오버헤드 발생 가능
• 하드웨어에서는 비트 플래그, 시간 스탬프 등을 자주 사용

📦 Cache Block Size란?

📏 블록 사이즈란?

• 캐시는 메모리를 바이트 단위가 아닌 "블록 단위"로 가져옵니다.
• 이 블록 하나에 담긴 데이터의 크기를 캐시 블록 크기(Cache Block Size)라고 합니다.

📈 블록 사이즈를 키우면?

장점	단점
공간 지역성 활용 ↑ (근처 데이터도 한꺼번에 가져옴)	블록이 너무 크면 캐시 낭비 증가 (필요 없는 데이터까지 로드)
적은 횟수로 캐시 적중 가능	캐시 블록 수 감소 → 충돌 가능성 증가

적절한 블록 크기를 설정하는 것이 매우 중요합니다!

읽어보기 좋은 글

• 메모리 계층 구조

기본 데이터 타입: 컴퓨터가 이해하는 '재료의 단위'

모든 데이터는 어떤 '형태'를 가지고 있어야 컴퓨터가 이해할 수 있어요. 이게 바로 데이터 타입입니다.

📦 데이터 타입이 중요한 이유

• 크기(size): 몇 비트로 구성되었는가? (int, char, float 등)
• 해석(interpretation): 부호가 있는 정수인가? 실수인가? 포인터인가?

예시: C 언어에서 자주 보는 데이터 타입들

• char : 1바이트 문자
• int : 보통 4바이트 정수
• float : 4바이트 실수
• double : 8바이트 실수
• void* : 주소를 담는 포인터

🧠 참고: 포인터(pointer)는 주소를 저장하는 변수로, '저기에 있는 값을 가져와'라고 말하는 역할을 합니다. 집 주소 같은 개념이죠!

💡 포인터 vs 참조

• 포인터는 주소를 직접 저장하고 조작합니다.
• 참조(reference)는 좀 더 안전한 개념으로, 포인터의 위험성을 줄이기 위해 등장했어요.

의문 : 자바스크립트는 타입이 없습니다. 그럼 과연 자바스크립트는 어떤식의 크기를 저장할지 어떻게 아는 걸까요? 그리고 그거 외의 프로그래밍은??

💬 모든 데이터는 결국 '비트 덩어리'

컴퓨터 입장에서 보면, 우리가 무엇이라 부르든 결국 모든 데이터는 0과 1의 조합, 즉 비트 스트림입니다.
그런데 이 0과 1을 '어떻게 해석하느냐'에 따라 정수가 될 수도 있고, 문자가 될 수도 있고, 이미지가 될 수도 있죠.

📦 데이터 타입은 왜 필요한가?

컴퓨터는 메모리에 저장된 이진수를 보면서 혼잣말로 이렇게 묻습니다:

"얘를 어떻게 읽어야 해?"

• 10000001 → 이게 부호 있는 정수? 부호 없는 정수? 문자? 실수?
• 따라서, 데이터를 올바르게 해석하려면 그 '형식(타입)'이 꼭 필요한 거예요.

🧮 C처럼 '타입이 명확한' 언어의 경우

C, C++, Java 등은 정적 타입 언어라고 불립니다. 컴파일할 때부터 각 변수의 타입이 명확하게 정해집니다.

int a = 42;
float b = 3.14;
char c = 'A';

이 말은, 컴파일러가 이미 변수의 크기(size)와 용도(interpretation)를 알고 있다는 뜻입니다.

• int: 4바이트로, 부호 있는 정수로 해석
• float: 4바이트지만, IEEE 754 방식의 실수로 해석
• char: 1바이트, ASCII 문자 코드로 해석

따라서 메모리 공간도 딱딱 정해진 크기와 방식으로 할당되죠.

🌈 자바스크립트처럼 '타입이 명확하지 않은' 언어는?

자바스크립트, 파이썬 등은 동적 타입 언어입니다. 즉, 변수에 타입을 지정하지 않고 값이 들어오는 순간 타입을 추론합니다.

let a = 42;      // number
a = "hello";     // string

그럼 자바스크립트는 "지금 a가 몇 바이트냐?"를 어떻게 알까요?

💡 답: 내부적으로 타입 + 값이 함께 저장되기 때문입니다. 이를 태깅(tagging) 기법이라고 불러요.

📌 예: JavaScript 내부 구조 (V8 엔진 기반)

let a = 3;

이 변수는 실제로 다음과 같은 형태로 저장됩니다:

[타입: Number][값: 3]

즉, 값을 저장할 때 '이건 number야', '이건 object야' 같은 메타 정보를 같이 붙여 저장하는 구조입니다.
값을 꺼낼 때도 자바스크립트 엔진은 먼저 타입 태그를 보고, 그에 따라 값의 크기나 해석 방식을 판단하죠.

하지만 내부적으로는 각 값의 타입과 크기를 관리해야 하므로, V8 엔진은 다양한 최적화 기법을 사용합니다.

자바스크립트에서 숫자 타입은 모두 IEEE 754 표준의 64비트 부동소수점 숫자(double)로 표현됩니다. V8 엔진은 메모리 효율성을 위해 최적화를 적용합니다.

V8 엔진은 태깅(tagging) 기법을 사용하여 값의 타입 정보를 함께 장니다.예를 들어, 포인터의 하위 비트를 사용하여 해당 값이 Smi인지, HeapNumber인지, 객체인지 등을 구분니다. 이를 통해 런타임에 빠르게 타입을 판별하고 적절한 처리를 할 수 있습니다

🔹 Smi (Small Integer)

• 작은 정수(예: 31비트 정수)는 힙에 할당하지 않고, 태그된 포인터(tagged pointer)로 직접 저장됩다.
• 이러한 값은 Smi(Small Integer)로 불리며, 메모리 공간을 절약하고 접근 속도를 높입니다.

🔹 HeapNumber

• Smi로 표현할 수 없는 숫자(예: 부동소수점 숫자, 큰 정수)는 HeapNumber 객체로 힙에 저장니다.
• 이 객체는 64비트 double 값을 포함하며, 추가적인 메타데이터를 가지고 있니다.

📦 자바스크립트에서의 메모리 크기비교

언어	정수 타입	메모리 크기	메모리 관리 방식
C	int	4바이트	고정 크기, 명시적 타입
Java	int	4바이트	고정 크기, 명시적 타입
JS	number	8바이트 (double)	동적 크기, 런타임 타입추론

자바스크립트는 변수 선언 시 타입을 명시하지 않기 때문에, 런타임에 값의 타입과 크기를 결정합니다.

이로 인해 메모리 사용이 유연하지만, 정적 타입 언어에 비해 메모리 오버헤드가 발생할 수 있습니다.

자바스크립트는 모든 숫자를 64비트 double로 표현하지만, V8 엔진은 작은 정수를 Smi로 최적화하여 메모리 효율성 높입니다.

📚 다른 언어들은 어떻게 할까?

언어	타입 지정 방식	크기 결정 시점	예시
C/C++	정적 타입	컴파일 타임	int a = 5;
Java	정적 타입 + 런타임 체크	컴파일 타임 + 런타임	int a = 5;
Python	동적 타입	런타임	a = 5
JavaScript	동적 타입	런타임	let a = 5
Rust	정적 타입	컴파일 타임 (엄격)	let a: i32 = 5;
Go	정적 타입 (자동 추론 가능)	컴파일 타임	var a = 5

🤔 요약해보면

• 정적 타입 언어는 컴파일러가 타입을 알고, 그에 따라 크기와 해석을 정함
• 동적 타입 언어는 런타임에 타입을 결정하며, 내부적으로는 태그 정보와 함께 저장
• 컴퓨터는 항상 비트를 1차원 메모리 공간에 저장하고, 데이터 타입을 통해 해석함

🏢 아파트에 비유한 배열과 메모리 이야기

1) 배열은 왜 아파트와 닮았을까?

프로그래밍 언어에서 데이터를 다루기 위해 사용하는 배열(array)은 마치 아파트와도 같습니다.

• 배열은 하나의 건물(기저 주소)을 중심으로
• 그 안에 같은 구조를 가진 집들(원소, element)이 차례로 줄지어 있는 형태입니다.
• 각 집에는 고유한 호수(index)가 있고, 이걸 통해 데이터를 구분합니다.

예를 들어, C언어에서 16비트 크기의 값을 저장하는 배열이라면
한 "집"은 2바이트이고, 10개의 집이 줄지어 있는 하나의 동(1차원 배열)처럼 볼 수 있죠.

2) 배열 속 메모리 구조 – 기저 주소와 오프셋

배열의 각 원소는 기저 주소(base address)를 기준으로 떨어져 있는 거리를 오프셋(offset)으로 계산합니다.

• 원소0의 주소가 100이면,
• 16비트(=2바이트) 크기일 때 원소1의 주소는 100 + 2 = 102가 됩니다.

즉, index × 데이터 타입의 크기 = 해당 원소의 오프셋

3) 배열은 못생긴 1차원 아파트? 다차원 배열로 확장!

1차원 배열은 층이 하나이고 집이 쭉 늘어선 못생긴 아파트 같지만,
현실 세계처럼 층과 동을 가진 2차원, 3차원, n차원 아파트 구조도 가능합니다.

배열 차원	아파트 비유
1차원	1개의 층에 집이 나란히 있는 복도형 아파트
2차원	층마다 여러 집이 있는 일반 아파트
3차원	여러 동이 있는 아파트 단지
4차원	단지 내 복합건물까지 포함한 메가타운 느낌

4) 배열 순회에도 "전단지 돌리기 요령"이 있다?

아래와 같은 2차원 배열(4층 × 3호)이 있다고 해볼게요.

이 배열을 순회하며 값을 처리한다는 건, 각 집에 전단지를 넣는 것과 같습니다.
그런데 순회 방식에 따라 성능이 크게 달라질 수 있어요.

▣ 순회 방법 두 가지

1. 열 우선(column major)
   → 0층 0호 → 1층 0호 → 2층 0호 … → 다시 0층 1호 → 1층 1호 …
2. 행 우선(row major)
   → 0층 0호 → 0층 1호 → 0층 2호 → 그다음 1층으로 이동

대부분의 언어(C, Python 등)는 행 우선(row major) 방식으로 배열을 메모리에 저장합니다.
이 방식은 참조 지역성(locality of reference)에 더 유리하죠.

5) 참조 지역성과 배열 순회의 관계

컴퓨터는 데이터를 읽을 때 가까운 메모리 위치를 더 빨리 읽습니다.
그래서 다음과 같은 원리가 적용돼요:

• 행 우선 순회는 인접한 메모리 공간에 있는 데이터를 계속 접근하게 되므로 캐시 효율이 높음
• 열 우선 순회는 메모리상으로 더 멀리 떨어진 데이터를 자주 접근하므로 캐시 효율이 떨어짐

6) 배열 접근과 보안 문제

배열 인덱스 범위를 벗어나는 접근은 심각한 버그와 보안 취약점을 일으킬 수 있습니다.

예:

int arr[10];  // 0~9까지 인덱스
arr[10] = 42; // 배열 바깥의 메모리에 접근 (20번째 바이트부터!)

• 파스칼, 자바처럼 인덱스를 자동으로 검사해주는 언어는 이런 접근을 막아줍니다.
• C, C++처럼 인덱스를 검사하지 않는 언어에서는 개발자가 직접 조심해야 합니다.

이처럼 프로그래밍 시에는 항상 배열의 길이와 인덱스 범위를 정확히 지키는 습관이 중요합니다.

7) 근데 그거 알아요? 메모리는 1차원이래(속닥속닥)

어? 근데 우리 2차원 배열도 처리했잖아?? 읭 그럼 그거는 뭔데

배열은 2차원 배열, 3차원 배열과 같이 다차원 배열을 사용할 수 있어요.

하지만 컴퓨터 메모리의 구조는 1차원이므로 2차원, 3차원 배열도 실제로는 1차원 공간에 저장합니다. 다시 말해 배열은 차원과는 무관하게 메모리에 연속 할당됩니다!

컴퓨터는 2차원 배열도 1차원으로 봅니다. 우리가 보는 것과 컴퓨터가 처리하는 방식은 다르죠

📌 우리는 '2차원 배열'을 이렇게 봅니다

우리가 코드를 작성할 때 이런 식으로 2차원 배열을 선언하곤 하죠:

int arr[2][2];

이 배열은 마치 2층짜리 아파트에 각 층마다 두 개의 집이 있는 구조처럼 보입니다.

arr[0][0]   arr[0][1]  
arr[1][0]   arr[1][1]

이처럼 행(Row)과 열(Column) 이 있는 구조는 인간에게 직관적입니다. 하지만!

📌 컴퓨터는 '물리적 1차원 공간'에 배열을 저장합니다

컴퓨터가 데이터를 저장하는 메모리 공간은 물리적으로 1차원입니다. 다시 말해, 줄줄이 일렬로 이어진 공간에 값을 순서대로 넣습니다. 이건 메모리가 RAM이든 캐시든 다 마찬가지예요.

2차원 배열 arr[2][2]의 경우에도 실제 메모리에는 다음과 같은 순서로 저장됩니다:

&arr[0][0] → &arr[0][1] → &arr[1][0] → &arr[1][1]

즉, 행 단위로 순서대로 저장(row-major order) 됩니다.

🔍 실험으로 확인해보자!

다음은 실제로 주소를 출력해서 메모리에서 어떻게 저장되는지 확인하는 코드예요:

int arr[2][2], i, j;
for(i = 0; i < 2; i++){
    for(j = 0; j < 2; j++){
        printf("%p\n", &arr[i][j]);
    }
}

📎 결과 예시:

008FFE50
008FFE54
008FFE58
008FFE5C

주소가 4씩 증가하고 있다는 사실에 주목하세요. int는 4바이트이기 때문에 다음 원소는 이전 원소보다 4바이트 뒤에 저장되는 것이지요.

이 결과는 바로 2차원 배열도 메모리에선 1차원처럼 연속된 공간에 저장된다는 걸 증명해줍니다.

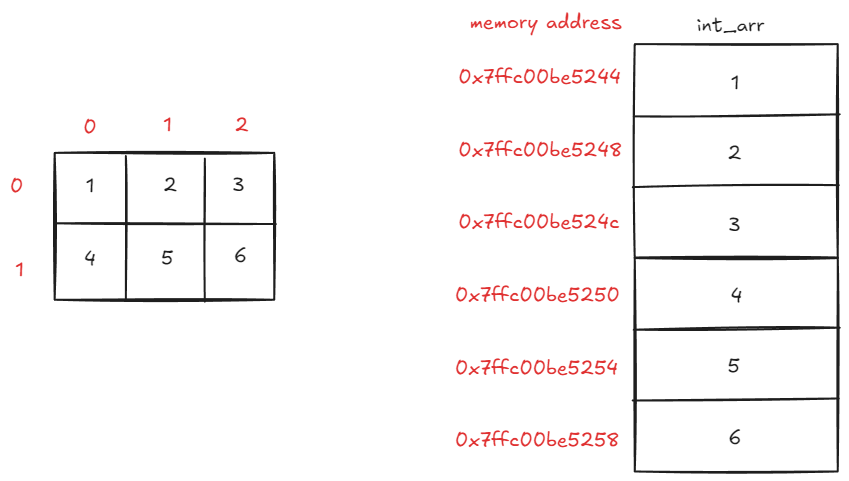
왼쪽은 2차원 배열을 사람이 이해하기 쉽도록 2차원으로 표현한 것이고, 오른쪽은 실제 메모리에 2차원 배열이 저장된 상태를 표현한 것입니다. 실제 메모리에는 1차원 공간에 연속적으로 저장합니다.

출처 : https://gideokkim.github.io/algorithm%20theory/array/

📌 3) 배열을 다룰 때 꼭 기억해야 할 점

구분	설명
2차원 배열 선언	int arr[2][2];와 같이 사용
메모리 저장 순서	실제로는 arr[0][0] → arr[0][1] → arr[1][0] → arr[1][1] 순
주소 확인 방법	&arr[i][j]로 각 원소의 주소 확인
메모리는 1차원	CPU는 메모리를 1차원 공간으로 취급
반복문 처리 순서	이 구조를 반영해서 for(i){ for(j){ ... }} 순으로 접근하면 효율적

🧩 기억해둘 개념들

• %p : C 언어에서 주소를 출력할 때 사용하는 포맷
• &연산자 : 변수의 주소를 가져오는 연산자
• Row-Major Order : 행 단위로 메모리에 배열을 저장하는 방식 (C언어 기본)
• Column-Major Order : 열 단위로 저장하는 방식 (Fortran 같은 언어에서 사용)

🤔 왜 이걸 알아야 할까요?

• 캐시 효율 향상
  → 연속된 메모리에 접근하면 CPU 캐시가 효율적으로 작동합니다.
  → 참조 지역성(Locality of Reference) 이라는 개념과도 연결됩니다.

• 성능 최적화
  → 메모리 접근 패턴에 따라 프로그램 성능이 달라집니다.
  → 배열을 ‘행 우선’으로 순회할 때 성능이 더 좋아지는 이유!

Memory Layout of C programming

출처 : https://blog.naver.com/newbongman/223457943042

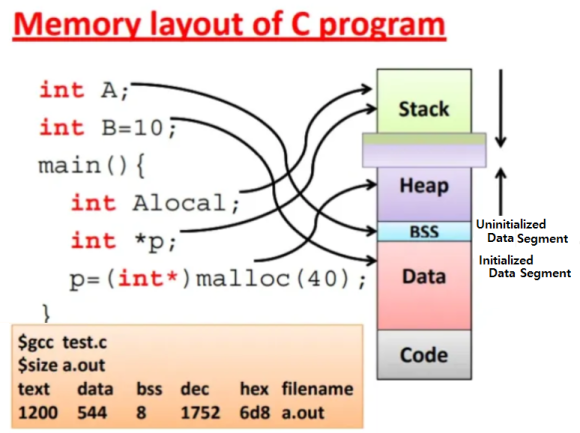
메모리라고 지칭하는 것

여기서 잠깐 우리는 가상메모리, 캐시메모리, 주기억장치 등 여러가지를 배웠어요."컴퓨터 메모리의 구조는 1차원"이라고 말할 때, 일반적으로 어떤 메모리를 말할까요?

이 '메모리'는 일반적으로 'RAM(주기억장치)'를 말합니다.

💡 1차원이라는 메모리 구조

메모리 종류	일반적으로 말하는 "1차원 주소 공간"에 해당?	설명
RAM (주기억장치)	✅ 맞아요!	프로그램이 실행되는 동안 데이터를 읽고 쓰는 실질적인 작업 공간입니다. 주소가 순차적으로 1차원처럼 배치되어 있어요.
레지스터	❌ 아니에요	CPU 내부의 소규모 저장 공간입니다. 주소 공간이라는 개념보다는 직접 명시된 이름으로 접근해요.
캐시 메모리	⭕ 어느 정도는	구조는 1차원일 수 있지만, CPU가 RAM보다 빠르게 접근하기 위한 중간 저장소입니다. 보통 주소보다는 태그 기반으로 데이터 위치를 관리합니다.
ROM	❌ 아니에요	읽기 전용 메모리로, 주소 공간 개념은 있지만 고정된 펌웨어만 읽습니다.
HDD / SSD (보조기억장치)	❌ 아니에요	주소 공간 개념이 파일 시스템에 가깝고, 메모리처럼 1차원적으로 직접 접근하는 방식은 아닙니다.

컴퓨터 구조에서 “1차원 메모리 주소 공간”이라는 표현은 보통 RAM (주기억장치)을 의미합니다.

• 주소는 0번부터 시작해서 0x0000, 0x0001, 0x0002… 이런 식으로 순차적으로 증가하며
• 이 주소를 통해 CPU가 데이터를 읽고 씁니다.
• 우리가 배열을 선언하면, 이 배열은 RAM 안의 연속된 주소 공간에 저장돼요.

🔍 비유로 이해하면?

• RAM은 단순한 창고입니다. 창고에는 1번 칸, 2번 칸, 3번 칸처럼 주소가 쭉 늘어서 있어요.
• 배열은 이 창고 안의 연속된 칸을 쓰는 것이고, CPU는 주소(칸 번호)를 통해 그 내용을 꺼내죠.
• 레지스터는 창고 밖에서 바로 옆에 붙은 도구함,
  캐시는 창고에서 자주 쓰는 물건만 따로 빼놓은 선반,
  HDD는 창고 옆에 있는 외부 창고쯤으로 보면 됩니다.

📌 그럼 가상 메모리는 1차원인가요?

결론부터 말하면, '가상 메모리 주소 공간 자체는 1차원적 구조입니다.'
즉, 논리적으로는 0번지부터 시작하는 긴 일렬의 주소들로 구성되어 있어요.

하지만...

💡 이 1차원 주소가 실제로 물리 메모리에 저장될 때는 '비연속적'일 수도 있습니다.

✅ 가상 메모리는 프로세스마다 갖는 '논리적인 주소 공간'입니다.

• 프로세스 입장에서 보면 "내 메모리 공간"은 마치 0번지부터 쭉~ 이어진 큰 연속 공간이에요.
• 그래서 배열도 0, 1, 2, 3 이렇게 인덱스를 부여하고 순차적으로 접근합니다.

  즉, 프로그래밍 관점에서 보면 1차원 메모리 구조입니다.

🔍 그런데 실제 물리 메모리에서는?

가상 메모리는 페이지 단위로 나뉘어서 → 물리 메모리의 아무 곳이나 매핑돼요!

• 예를 들어, 가상 주소 0x0000~0x0FFF는 물리 주소 0x9C00~0x9FFF와 연결될 수 있어요.
• 즉, 가상 주소는 연속적이지만, 물리 주소는 불연속적일 수 있습니다.

🧠 이 매핑을 담당하는 게 바로 페이지 테이블(Page Table)이고,
이를 통해 OS는 주소 변환을 해줍니다.

✏️ 비유로 이해하기

가상 메모리를 아파트 평면도라고 해봅시다.

• 가상 메모리: "0호, 1호, 2호, 3호..." 순서대로 평면도에 있음
• 물리 메모리: 실제 건물은 그 순서대로 짓지 않았음 (0호 다음이 꼭 1호 아니고, 여기저기 흩어져 있음)
• 페이지 테이블은 “평면도에 있는 방 → 실제 위치”를 연결해주는 네비게이션입니다.

8) 메모리 지역성을 잘 활용하는 법

2차원 배열을 생각해봅시다.

🧾 전단지를 돌리려면, 한 층을 먼저 다 돌리고 올라가는 게 효율적이겠죠? 바로 이게 메모리 지역성을 잘 활용하는 방법입니다.

행 우선(row major) 저장 방식

인덱스	메모리 주소 기준 상대 위치
(0,0)	0
(0,1)	1
(0,2)	2
(1,0)	3
(1,1)	4

이처럼 열보다 행을 먼저 바꾸는 방식이 지역성이 좋기 때문에 일반적으로 더 효율적입니다.

배열 인덱스 오류: 경계 체크가 없으면?

예를 들어 C 언어에서는 배열 범위를 벗어나도 오류가 발생하지 않을 수 있습니다. 아래 코드를 보세요:

int arr[5];
arr[10] = 42; // 위험한 코드!

이렇게 하면 프로그램이 다른 메모리를 침범해서, 예기치 않은 동작이나 보안 취약점을 만들 수 있어요.

🧠 파스칼이나 자바는 배열 경계를 체크하지만, C/C++은 성능을 위해 하지 않아요. 그래서 여러분이 직접 조심해야 합니다.

🧠 비트 하나로 8명을 관리하는 법? – 비트맵(bitmap)의 세계

📌 1) 왜 비트맵이 필요할까?

여러분이 산타클로스라고 생각해보세요. 🎅 전 세계의 착한 아이들과 나쁜 아이들을 구분하고 싶어요. 그럼 사람마다 착함(true) 혹은 나쁨(false)만 표시하면 되겠죠? 이럴 때 1비트만 있으면 충분합니다!

그런데 일반적으로 사용하는 char 타입은 8비트예요. 아이 한 명에 char 하나를 쓰면 1명이 8비트를 통째로 차지하게 되죠. 너무 아깝잖아요?

그래서 등장한 게 비트맵(Bitmap) 입니다.
즉, 비트 단위로 배열을 구성해서 저장 공간을 아껴 쓰는 기법이에요.

🧱 2) 비트맵 구조 – 바이트 안에 8개의 상태를 넣자!

예를 들어 35명의 상태를 추적하고 싶다면, 몇 개의 바이트가 필요할까요?

📏 35비트 ÷ 8비트 = 4.375 → 5개의 바이트로 충분합니다!

이렇게 각 바이트가 8개의 사람 정보를 저장할 수 있으니,
5개의 바이트 = 40비트로 충분하죠.

Byte 0: Bit 0 ~ 7
Byte 1: Bit 8 ~ 15
Byte 2: Bit 16 ~ 23
Byte 3: Bit 24 ~ 31
Byte 4: Bit 32 ~ 34 (나머지 여유 있음)

🔧 3) 비트를 조작하는 네 가지 방법

이제 비트를 설정, 해제, 확인하려면 어떻게 해야 할까요?

🛠 비트 연산 요약:

동작	연산 방식
비트 켜기 (1로 만들기)	`bitmap[i]
비트 끄기 (0으로 만들기)	bitmap[i] &= ~mask;
비트가 1인지 검사	(bitmap[i] & mask) != 0
비트가 0인지 검사	(bitmap[i] & mask) == 0

🧮 4) 비트 마스크는 이렇게 만들어져요

예: 17번째 비트를 조작하고 싶다면?

1) 먼저, 17 / 8 = 2 → 3번째 바이트에 존재
2) 마스크 만들기

• 17 & 0x07 = 1
• 1 << 1 = 00000010 → 마스크 완성!

즉, 17번째 비트를 조작하려면 3번째 바이트에서 00000010을 활용하면 됩니다.

🧵 5) 자원 할당 문제에도 유용한 비트맵

예를 들어 운영체제에서 파일 디스크 블록을 관리한다거나,
메모리 블록이 사용 중인지 아닌지를 추적할 때도 비트맵을 씁니다.

✅ 0이면 사용 가능
❌ 1이면 사용 중

이걸 검사해서 “어느 비트가 0이지?”를 빠르게 찾을 수 있습니다.

📌 이때는 unsigned long long 같이 큰 타입을 써서 64비트를 한 번에 처리하면 훨씬 효율적이에요!

6) 🎨 팔레트를 사용하는 비트맵(Bitmap) 영상이란?

우리가 일반적으로 아는 비트맵 이미지는 픽셀마다 직접 RGB 색상 값을 저장하죠.
하지만 1비트, 4비트, 8비트 비트맵은 픽셀마다 색 자체가 아닌 ‘색의 번호(인덱스)’를 저장해요.

✍️ 비유해서 설명하면?

• 색상 테이블(Palette)은 물감 팔레트 같은 거예요.
• 픽셀은 물감 색을 지정하는 번호만 가지고 있어요.
• 그림 그릴 때, "2번 물감 써줘!"라고만 말하는 셈이에요.

🧠 동작 원리

1️⃣ 색상 테이블(Palette)

typedef struct tagRGBQuad {
	BYTE rgbBlue;
	BYTE rgbGreen;
	BYTE rgbRed;
	BYTE rgbReserved; // 항상 0
}

• 색 하나를 4바이트(R, G, B, reserved)로 표현
• 예: (255, 0, 0, 0) → 빨강

2️⃣ 인덱스로 색을 지정

• 픽셀 값 = 팔레트 색상의 인덱스
• 인덱스를 통해 팔레트 테이블을 조회해서 진짜 색을 꺼내요.

🖼️ 예시

예를 들어, 픽셀 데이터에 254라는 숫자가 있으면
→ 팔레트의 254번째 칸에서 RGB 색상 R=178, G=75, B=62 값을 가져오는 거예요.

🧮 비트 수에 따른 색상 표현력

비트 수	표현 가능한 색 수	팔레트 크기(색상 수 × 4바이트)
1비트	2가지 (흑백 등)	2 × 4 = 8 bytes
4비트	16가지	16 × 4 = 64 bytes
8비트	256가지	256 × 4 = 1024 bytes

💡 색상이 다양해질수록 메모리 공간도 더 필요해요.

📌 왜 팔레트를 쓰나요?

• 장점

  • 적은 비트로 색 표현 → 메모리 절약
  • 동일한 색을 여러 픽셀이 공유할 수 있음
  • 특히 예전 PC에서 저용량 이미지에 적합

• 단점

  • 색상 표현의 한계 (최대 256색)
  • 이미지 품질 제한 (그라데이션 표현 어려움)

🖥️ 실제 저장 구조

이미지 2개를 보면 이해가 돼요:

1. 색상 테이블 + 인덱스 매핑 구조

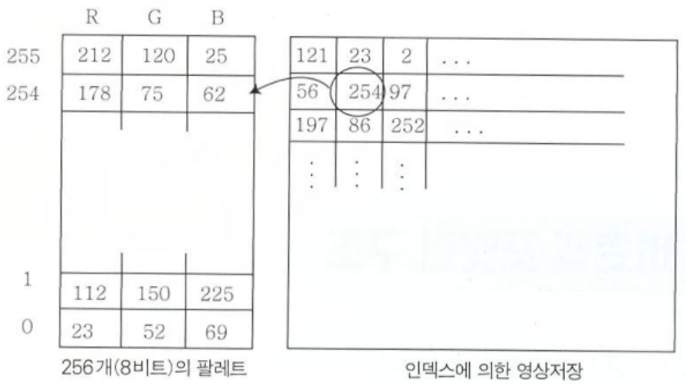
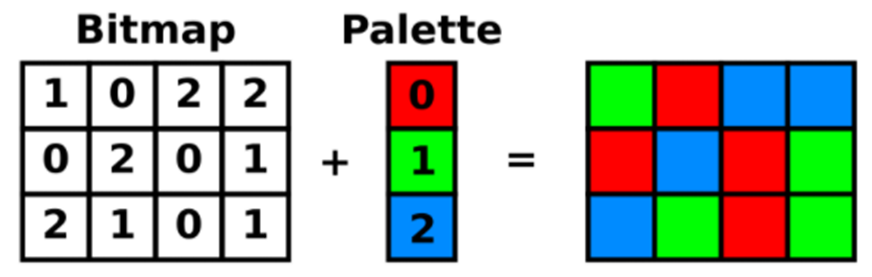
2. 팔레트 인덱스를 통한 컬러 매핑

🧵 문자열을 저장하는 컴퓨터의 방식 – C 언어의 이야기

📌 "Cheese"라는 말을 컴퓨터가 어떻게 저장할까?

우리는 “치즈”라는 말을 보면 6개의 문자로 된 단어라는 걸 쉽게 알 수 있죠.
그런데 컴퓨터는 문자 하나하나를 바이트 단위로 저장하고, 또 이 문자열의 끝이 어딘지를 알아야 출력이나 연산을 제대로 할 수 있습니다.

그럼, 어떻게 해야 컴퓨터가 문자열의 "끝"을 알 수 있을까요?

1️⃣ 문자열의 끝을 저장하는 두 가지 방식

🅰️ 방법 1: 길이를 먼저 저장한다

• 첫 번째 바이트에 “길이 정보”를 저장합니다.
• 예: "Cheese"라는 단어가 있으면, 6을 맨 앞에 저장하고, 그 뒤에 C, h, e, e, s, e가 오게 하죠.

[6][C][h][e][e][s][e]

단점은?

• 길이를 저장하는 바이트 수에 제한이 있어요. 1바이트면 최대 255글자밖에 못 저장해요.
• 만약 1000자 넘는 글자가 필요하면 길이 표현을 위해 2~4바이트를 써야 하니까, 그만큼 낭비가 생기죠.
• 또 길이 바이트는 메모리 정렬(Alignment)을 고려해서 넣어야 하므로, 구현이 까다로워요.

🅱️ 방법 2: 끝에 '0'을 넣는다 (C 언어 방식)

C 언어는 훨씬 단순한 방법을 택했습니다.
바로 문자열이 끝났다는 것을 나타내는 특수한 문자인 NUL 문자 (0)를 맨 끝에 추가하는 방식이에요!

예:

[C][h][e][e][s][e][\0]  ← \0은 NUL (값이 0인 문자)

이런 방식 덕분에 문자열의 길이를 미리 몰라도, 컴퓨터는 NUL 문자를 만날 때까지 하나씩 읽으면서 문자를 처리할 수 있어요.

2️⃣ 왜 하필 'NUL(0)'일까?

• 대부분의 컴퓨터는 "값이 0인지 아닌지"를 한 번의 비교 연산으로 아주 빠르게 할 수 있어요.
• 그래서 "문자열 끝이 0이야" 라고 정해두면 성능에도 유리하죠.
• 다른 문자를 끝 표시로 사용하면, 그걸 하나하나 읽어서 비교해야 하니까 훨씬 느려져요.

✅ 장점과 단점

항목	설명
✅ 장점	- 구조가 단순해요 (길이 저장 안 해도 됨) - 문자열 출력이 빠름 (끝까지 읽으면 됨)
⚠️ 단점	- 문자열 길이를 계산하려면 전부 스캔해야 함 - 중간에 \0 문자를 포함할 수 없음

3️⃣ 예시 코드

#include <stdio.h>

int main() {
    char str[] = "Cheese";
    printf("%s\n", str);  // Cheese 출력됨
}

• 실제 메모리 구조는 아래처럼 생겼을 거예요:

주소	값 (아스키)
0x00	C (67)
0x01	h (104)
0x02	e (101)
0x03	e (101)
0x04	s (115)
0x05	e (101)
0x06	\0 (0)

🔍 부가 개념: 문자열 vs 배열

• 문자열은 끝에 \0이 있는 문자 배열입니다.
• 즉, "Hello"는 [H][e][l][l][o][\0]와 같고,
• char arr[6] = {'H', 'e', 'l', 'l', 'o', '\0'} 도 같은 결과를 가져옵니다.

📌 자바스크립트나 파이썬은 왜 이런 걸 신경 안 쓸까?

자바스크립트, 파이썬 같은 고수준 언어에서는 문자열을 직접 메모리에 저장하는 방식까지 신경 쓰지 않아도 되기 때문이에요.

• 이들 언어는 내부적으로 문자열 객체에 길이 정보 + 문자들을 구조체처럼 갖고 있습니다.
• 문자열 길이는 항상 추적되고 있고, 끝을 굳이 0으로 표시하지 않아도 되죠.

📦데이터 구조와 처리 – 스위트룸부터 픽셀까지

1. 구조체란 무엇인가요? – 호텔 스위트룸의 비유

여러분, 간단한 짐을 잠깐 보관하려면 그냥 사물함 하나면 되겠죠.
하지만 좀 더 멋진 숙소, 예를 들면 호텔 스위트룸을 원할 수도 있어요.

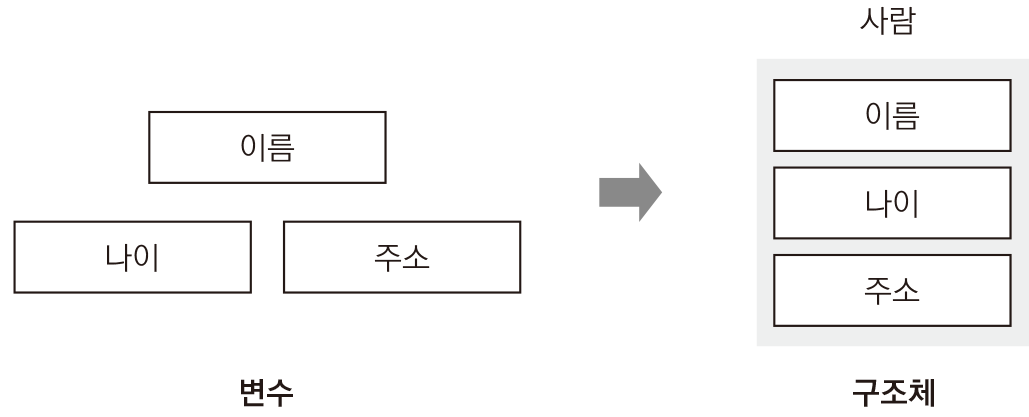
구조체(Structure)는 바로 그런 스위트룸 같은 공간입니다.

• 단순 변수: 작은 사물함 → 한 개의 값만 저장
• 구조체: 스위트룸 → 여러 방(=멤버)을 가진 하나의 공간

즉, 구조체는 우리가 여러 데이터를 함께 묶어 하나의 타입처럼 사용하는 방법이에요.
스위트룸의 각 방은 구조체의 멤버(member)라고 보면 됩니다.

2. 📅 일정관리 프로그램을 만든다면?

예를 들어, 일정관리 앱을 만든다고 해볼게요.

• 각 이벤트마다 시작 시각, 종료 시각이 필요하겠죠?
• 각각은 ‘월, 일, 시, 분, 초’ 정보로 구성될 수 있어요.

#include <stdio.h>

struct datetime {
    unsigned char hours;    // 1 byte
    unsigned char minutes;  // 1 byte
    unsigned char seconds;  // 1 byte
    unsigned short year;    // 2 byte
    unsigned char month;    // 1 byte
    unsigned char day;      // 1 byte
};

int main() {
    struct datetime dt = {10, 30, 45, 2024, 4, 16};
    unsigned char *ptr = (unsigned char*)&dt;

    for (int i = 0; i < sizeof(dt); i++) {
        printf("Byte %2d: 0x%02X\n", i, ptr[i]);
    }

    return 0;
}

이렇게 하면, 날짜와 시간을 하나의 타입으로 깔끔하게 묶을 수 있습니다.

구조체를 사용하면 코드를 훨씬 읽기 쉽게 만들 수 있어요.

관련하여 구조체의 실제 덤프 분석

필드	타입	크기(Byte)
hours	unsigned char	1
minutes	unsigned char	1
seconds	unsigned char	1
패딩	(자동 삽입)	1
year	unsigned short	2
month	unsigned char	1
day	unsigned char	1
합계		8 byte

🔎 메모리 덤프 출력 예시

만약 dt = {10, 30, 45, 2024, 4, 16} 라면, 아래처럼 나옵니다:

Byte  0: 0x0A   // hours = 10
Byte  1: 0x1E   // minutes = 30
Byte  2: 0x2D   // seconds = 45
Byte  3: 0x00   // padding (자동 정렬용, 비어있는 공간)
Byte  4: 0xE8   // year = 2024 (0x07E8) → little endian 하위 바이트
Byte  5: 0x07   // year 상위 바이트
Byte  6: 0x04   // month = 4
Byte  7: 0x10   // day = 16

✨ 주의할 점: unsigned short인 year는 리틀 엔디안 시스템에서 하위 바이트가 먼저 저장됩니다.

💡 왜 padding이 들어갔을까?

unsigned short year는 2바이트 정렬 기준(2-byte aligned)을 따라야 하므로,
그 전에 오는 unsigned char 3개 이후, 1바이트를 비워 정렬 위치(4번지부터)를 맞춥니다.

이러한 정렬은 메모리 접근 성능 향상을 위해 대부분의 컴파일러가 자동으로 처리해줍니다.

🧰 컴파일러가 padding 넣는 이유 요약

목적	설명
정렬(alignment)	CPU가 2/4/8 바이트 단위로 정렬된 데이터에 접근할 때 훨씬 빠릅니다.
성능 향상	정렬되지 않으면 CPU가 여러 번 메모리에 접근해야 함
구조체 크기 보정	필드 간 정렬을 위해 중간에 공간을 비워둠 (padding)

📦 정리: 구조체 메모리 덤프 한눈에 보기

위치 (Byte)	내용	값	설명
0	hours	0x0A	10
1	minutes	0x1E	30
2	seconds	0x2D	45
3	padding	0x00	정렬용 공간
4	year (LSB)	0xE8	2024의 하위 바이트
5	year (MSB)	0x07	2024의 상위 바이트
6	month	0x04	4
7	day	0x10	16

3) 🍬 편의 문법(Syntactic Sugar)이란?

영국의 컴퓨터 과학자 피터 란딘(Peter Landin)은
프로그래밍을 더 '달콤하게' 만들어주는 문법들을 편의 문법(Syntactic Sugar)이라고 불렀어요.

예를 들어,

• a = a + 1 → a += 1 → a++
• 배열의 모음 → 구조체 배열로 대체

사용하지 않아도 되지만, 사용하면 훨씬 더 명확하고 편리한 코드가 됩니다.

4) 🧠 메모리는 생각보다 까다롭다 – 정렬(Padding) 개념

하나 더 짚고 넘어갈 게 있어요. 구조체를 선언하면,
우리가 쓴 순서대로 메모리에 바로 붙여서 들어가는 건 아닙니다.

왜냐고요?

컴퓨터는 정렬된 메모리를 훨씬 빠르게 처리할 수 있기 때문이에요.

예시: 구조체 메모리 배치 (32비트 기준)

멤버	크기(Byte)
hours	1
minutes	1
seconds	1
패딩	1
year	2
month	1
day	1

총 8바이트로 정렬됩니다. (원래는 7바이트만 써도 됨)

이런 정렬 덕분에 CPU는 더 빠르게 구조체 데이터를 가져올 수 있어요.

5)⌛ 구조체 + 문자열의 조합

struct event_entry {
  struct datetime start;
  struct datetime end;
  char event_name[16];
};

하나의 이벤트를 표현하기 위해
시간 정보 두 개(start, end)와 이벤트 이름 문자열을 함께 담고 있어요.

이제 event_entry 구조체 배열을 만들면?
바로 달력이 되는 거죠!

6) 🧨 공용체(Union)란? – 한 공간을 여러 시선으로 보기

이번에는 조금 다르게,
하나의 메모리를 여러 관점으로 나눠 쓰는 방식도 있어요.

이걸 공용체(union) 라고 합니다.

🧫 공용체 vs 구조체

특징	구조체(struct)	공용체(union)
메모리 사용	각 멤버가 독립된 공간	모든 멤버가 같은 공간 공유
대표 사례	달력 이벤트 구조체	픽셀 데이터 (색 표현 등)

예시: 픽셀 색상 표현 공용체

union pixel {
  unsigned long color; // 전체 픽셀 값 (32bit)
  struct {
    unsigned char red;
    unsigned char green;
    unsigned char blue;
    unsigned char alpha;
  } components;
};

이렇게 하면 pixel.color = 0x12345678 으로 설정하면

• red = 0x12
• green = 0x34
• blue = 0x56
• alpha = 0x78

동일한 공간을 전체 색상값 또는 RGBA 컴포넌트 각각으로 접근할 수 있어요!

7) ⏳ 실제 시간 표현은 어떻게?

현대 시스템에서는 시간을 구조체보다 간단하게 표현하기도 해요.
예를 들어 Unix Time을 기준으로,

1970년 1월 1일 0시 0분 0초부터 몇 초가 흘렀는지 32비트 정수로 표현합니다.

unsigned int timestamp;  // 예: 1649904000 (2022-04-15)

많은 시스템이 2038년 문제를 해결하기 위해 64비트 확장을 사용 중이에요.

✨ 요약

개념	설명
구조체	여러 멤버를 하나의 타입으로 묶는 고급 데이터 구조
편의 문법	필수는 아니지만 사용하면 코드를 읽기 쉽고 간결하게 만듦
패딩	메모리 정렬을 위해 자동 삽입되는 빈 공간
공용체	동일한 메모리를 다양한 방식으로 해석 가능
유닉스 타임	1970년부터의 초 단위 시간 표현 (epoch)

복합 데이터 타입 구조체에 대한 의문

의문 : 구조체 변수를 한 번에 묶는다고 했는데 함수로 묶어도 되는거 아닌가요?

✅ 구조체와 함수, 언제 어떻게 묶을까?

1) 구조체는 데이터(변수)를 묶는 것

struct Point {
    int x;
    int y;
};

• x, y처럼 서로 관련된 데이터를 하나의 묶음으로 관리할 수 있도록 도와주는 게 구조체입니다.
• 예를 들어, x=10, y=20이라는 점(Point)을 표현할 때 매번 따로 변수로 넘기기보다 struct Point p = {10, 20};처럼 묶어서 관리하는 게 훨씬 편하죠.

2) 함수는 행동(로직)을 묶는 것

void printPoint(struct Point p) {
    printf("(%d, %d)", p.x, p.y);
}

• 함수는 "무엇을 한다"는 동작을 묶는 것입니다.
• print, 계산, 판단 등 어떤 동작을 하나로 모아두는 방식이죠.
• 물론 함수 안에서 구조체를 인자로 받아 사용할 수는 있지만, 함수가 데이터를 묶는 역할은 하지 않습니다.

"구조체는 함께 다녀야 하는 짐(데이터)을 캐리어에 담는 것"
반면에,
"함수는 이 짐을 들고 어디론가 이동하는 로직"이라고 할 수 있어요.

그럼에도 함수를 변수로 묶는 것은?

다만 "함수로 변수를 묶는다"는 표현은 정확히 말하면 "함수 안에 지역 변수들을 함께 사용한다"는 의미로 해석될 수 있어요. 구조체처럼 변수들을 정의 자체로 묶는 건 아니지만, 함수 내부에서 함께 사용하는 형태로 변수들을 "묶어 쓴다"는 관점에서 예시를 보여드릴게요.

✅ 함수 안에서 변수를 함께 묶어 사용하는 예시

#include <stdio.h>

void calculateRectangle() {
    int width = 5;
    int height = 3;

    int area = width * height;
    int perimeter = 2 * (width + height);

    printf("넓이: %d\n", area);
    printf("둘레: %d\n", perimeter);
}

• width, height, area, perimeter는 모두 '사각형'이라는 맥락에서 관련된 변수들입니다.
• 이들을 하나의 함수로 묶어서 계산과 출력을 동시에 수행하죠.

🆚 구조체를 사용한 버전

같은 맥락을 구조체로 묶는다면 이렇게 됩니다:

#include <stdio.h>

struct Rectangle {
    int width;
    int height;
};

void printRectangleInfo(struct Rectangle r) {
    int area = r.width * r.height;
    int perimeter = 2 * (r.width + r.height);

    printf("넓이: %d\n", area);
    printf("둘레: %d\n", perimeter);
}

• Rectangle이라는 구조체로 관련 데이터(width, height)를 정의하고,
• printRectangleInfo()라는 함수로 이 구조체를 인자로 받아 동작을 정의합니다.

방식	설명	장점	한계
함수 내부에 변수 묶기	calculateRectangle()처럼 함수 안에서 변수들 함께 사용	간단한 계산이나 로직 처리에 유용	변수 재사용이나 데이터 전달이 어렵다
구조체로 변수 묶기	struct Rectangle을 정의하여 관련 데이터 하나로 표현	재사용성 높고 다양한 함수에 전달 가능	초기 학습 시 복잡하게 느껴질 수 있음

함수 안에서도 관련된 변수들을 함께 "논리적으로 묶어" 사용할 수는 있지만,
진짜 물리적으로 묶고 재사용하고 싶다면 → 구조체를 사용하는 것이 더 좋습니다.

의문 : 구조체 말고 변수를 다양한 복합 데이터를 넣고 싶다면 map도 객체를 넣는 거니 어쩌면 맞지 않나요?

네, 맞습니다. 구조체가 아닌 방식으로 여러 종류의 데이터를 하나로 묶고 싶다면, Map, Object, Dictionary 같은 컬렉션 기반 자료구조도 충분히 좋은 대안이 될 수 있습니다.
다만 언어마다 그 사용 방식과 의미는 조금씩 다르니, 아래에서 차근차근 비교해볼게요!

✅ 구조체 vs Map/Object/Dictionary

구분	구조체 (C 언어 기준)	Map / Object / Dictionary
개념	정해진 필드 이름으로 구성된 데이터 묶음	키-값 쌍(key-value) 형태의 유연한 데이터 묶음
선언 방식	컴파일 타임에 필드 고정	런타임에 키를 동적으로 추가 가능
데이터 타입	각 필드의 타입이 명확함	값마다 타입이 다를 수 있음 (특히 JS/Python)
예시 언어	C, C++, Rust 등	JavaScript, Python, Java 등
장점	타입 안정성, 성능 좋음	유연성, 확장성 좋음
단점	동적 키 추가 불가, 고정적 구조	타입 불안정, 오타에 취약함

🌰 예시로 비교해볼게요!

1) 구조체 – 정적인 구조

struct Student {
    char name[20];
    int age;
};

• name, age라는 고정된 필드가 존재
• 컴파일 타임에 구조가 정해져 있어서 빠름

2) 자바스크립트의 객체 – 동적인 구조

const student = {
  name: "Alice",
  age: 20,
  grade: "A+"
};

• 필드가 자유롭게 추가될 수 있고,
• student.hobby = "reading"처럼 나중에 넣는 것도 가능!

3) 파이썬의 딕셔너리 – 완전 유연

student = {
    "name": "Alice",
    "age": 20,
    "grade": "A+"
}
student["hobby"] = "reading"

• 키와 값을 자유롭게 추가 가능
• 다만 "age" → "agge" 오타 나면 디버깅 어려움

🔍 그렇다면 어떤 상황에서 Map/Object가 구조체를 대체할 수 있을까?

✅ Map/Object가 좋은 상황

• 데이터 필드가 자주 바뀌는 경우
• 어떤 필드가 들어올지 정해지지 않은 외부 데이터 (ex. JSON 응답)를 처리할 때
• 빠르게 프로토타입을 만들거나, 가볍게 테스트할 때

✅ 구조체가 좋은 상황

• 데이터 타입이 정해져 있고, 구조가 안정적일 때
• 성능이 중요한 경우 (임베디드, C)

💡 비유로 쉽게 설명하면?

구조체	정해진 서랍장이 있는 서랍 (항상 같은 위치에 같은 물건)
Map/Object	자유롭게 라벨 붙여가며 물건 넣는 큰 박스 (유연하지만 정리 필요)

✅ 정리

Map/Object도 객체를 "동적으로" 구성하는 도구이며, 구조체처럼 "데이터를 묶는 역할"을 수행할 수 있습니다.
단, 목적이 다르기 때문에 안정성과 명확함을 원하면 구조체, 유연성을 원하면 Map/Object를 선택하는 것이 좋습니다.

연결리스트는 이전 자료구조에서 많이 공부해서 스킵

동적 메모리 할당

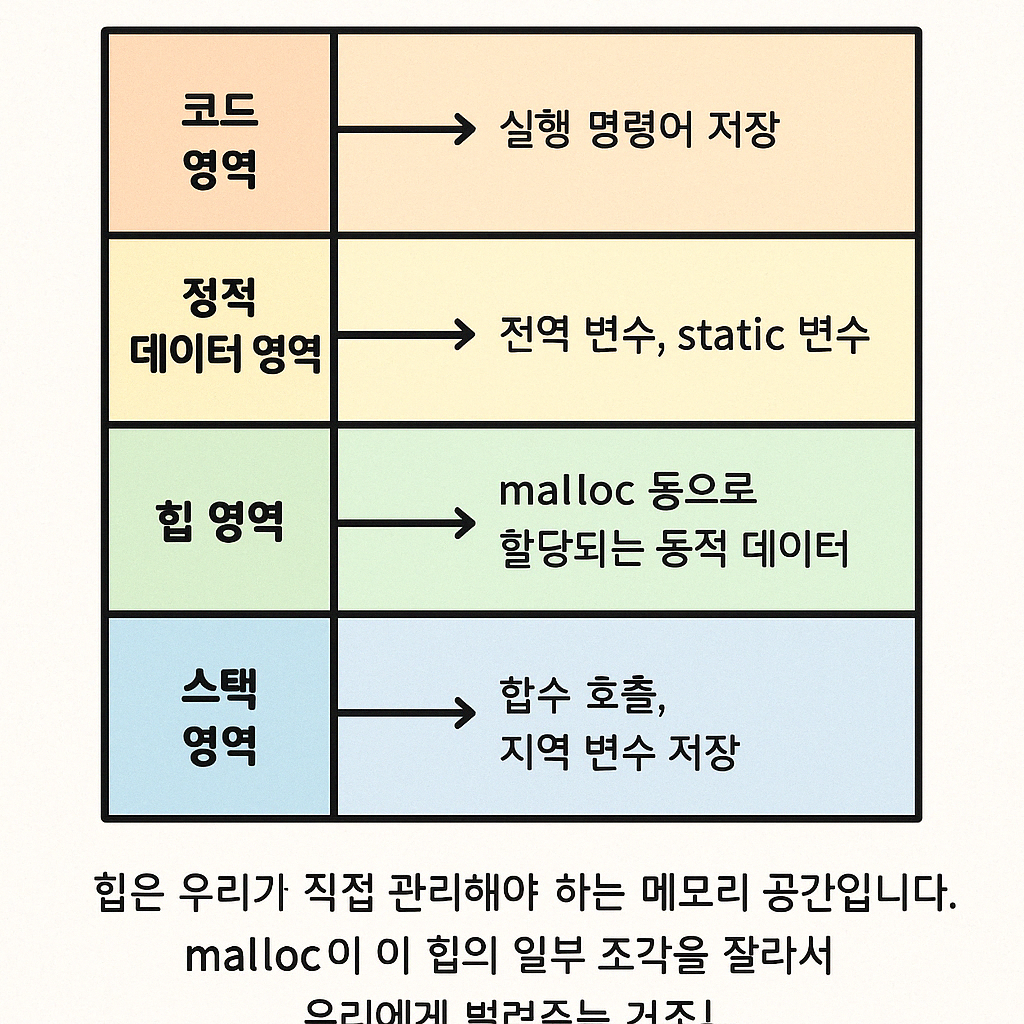
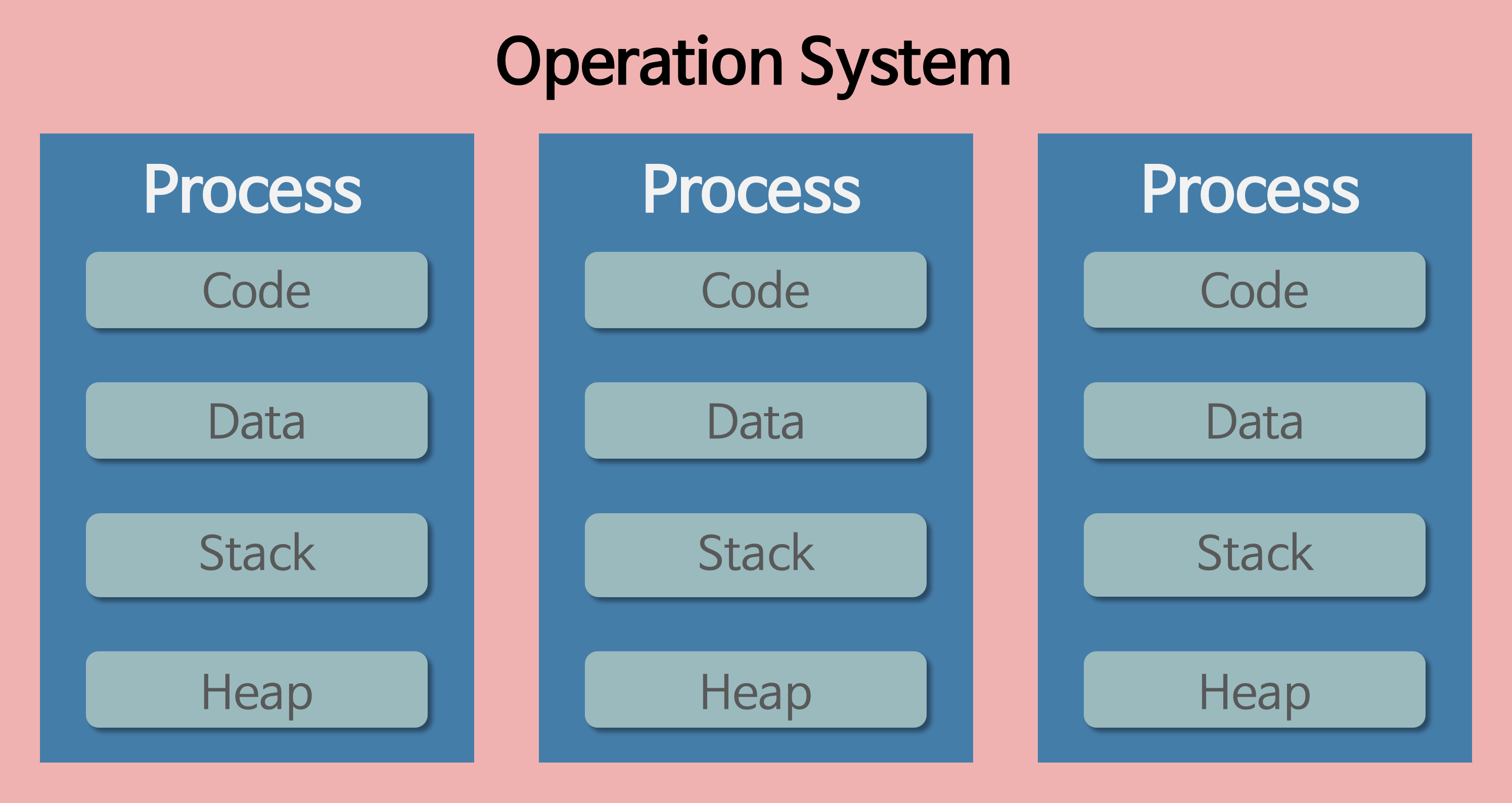
우리가 방금 본 코드 영역, 정적 데이터 영역, 힙, 스택은 사실 전부 하나의 프로세스 메모리 공간 내부에 포함되어 있는 구성 요소들이에요.

✅ “쟤네는 어디 메모리에 들어가 있어?”의 정답:

→ 프로세스가 운영체제로부터 할당받은 가상 메모리 공간 안에 들어 있어요.

📌 좀 더 구체적으로 정리하면?

1. 운영체제는 프로세스를 만들 때, 가상 주소 공간을 하나 통째로 할당해줍니다.
   예: 0x00000000 ~ 0xFFFFFFFF (32비트 기준, 4GB)

2. 이 가상 메모리 공간 안에 영역별로 구분해서 다음처럼 배치해요:

   메모리 영역	주요 내용
   코드 영역 (text segment)	컴파일된 명령어 (CPU가 실행할 코드)
   정적 데이터 영역 (data segment)	전역 변수, static 변수
   힙 영역 (heap)	동적 메모리 (malloc 등)
   스택 영역 (stack)	함수 호출 시 생성되는 지역 변수, 리턴 주소 등

3. 이 모든 구조는 하나의 프로세스 안에서 일어나는 일이고, 모두 가상 주소 기반으로 구성되어 있어요.

💡 잠깐! 그럼 진짜 메모리는 언제 쓰이나요?

• CPU가 실행하려면 실제 물리 메모리(RAM)를 써야 하니까,
  → 이 가상 메모리 주소들을 MMU(메모리 관리 유닛)가 물리 주소로 변환해줘요.

• 즉, 우리는 프로그래머 입장에서 가상 주소로만 편하게 생각하면 되고,
  운영체제와 하드웨어가 그걸 실제 RAM에 맞춰 매핑해서 동작하게 해주는 거예요.

🧠 요약

질문	답변
코드/힙/스택/데이터 영역은 어디 들어 있음?	프로세스의 가상 메모리 공간 안에 배치됨
실제 물리 메모리에선?	MMU가 가상 주소를 물리 주소로 매핑해서 RAM에 실제로 저장하고 실행함

여러 프로세스가 같은 코드 쓰면 메모리를 어떻게 아껴요?

현대 운영체제의 핵심 효율 기술 중 하나가 바로 이거예요:

✨ 여러 프로세스가 같은 프로그램을 실행해도, 메모리를 아끼는 방법
→ 바로 "코드 공유" 기법입니다.

예를 들어, 여러분이 메모장에서 3개의 파일을 각각 실행한다고 생각해보세요.
→ 사실 이건 같은 메모장 프로그램을 3개 띄운 것이에요.
→ 근데 그럼 메모리에 메모장 코드가 3번이나 올라가야 할까요?

❌ 그렇게 하면 메모리 낭비가 너무 심하죠.
✅ 그래서 운영체제는 코드 영역은 공유하고, 데이터는 분리해줘요.

🔍 운영체제의 절약 기술: 코드 공유 (text segment sharing)

✔️ 공유하는 것

• 코드 영역 (text segment)
  → 바이너리 실행파일로부터 읽은 명령어 부분은 변하지 않음 (read-only)
  → 그래서 여러 프로세스끼리 공유 가능함!

❌ 공유하지 않는 것

• 힙 영역, 스택 영역, 정적 데이터 영역
  → 각각의 프로세스마다 독립적으로 할당됨
  → 왜냐하면 변수 값이나 함수 호출 스택은 프로세스마다 다르니까!

📦 예시: 메모장 3개 실행 시 메모리 구성

메모리 영역	메모장 A	메모장 B	메모장 C
코드 영역 (text)	🟨공유	🟨공유	🟨공유
데이터 영역	🟦개별	🟦개별	🟦개별
힙	🟩개별	🟩개별	🟩개별
스택	🟥개별	🟥개별	🟥개별

💡 운영체제는 어떻게 공유하냐고요?

메모리 매핑 기술인 page table과 MMU 덕분이에요!

1. 운영체제는 실행파일(.exe, ELF 등)의 코드 부분을 메모리에 올릴 때
   → 이 코드 영역을 read-only로 표시하고
   → 여러 프로세스가 같은 물리 메모리 페이지를 가리키도록 설정합니다.

2. 각 프로세스의 페이지 테이블에
   → 동일한 물리 주소를 가상 주소에 매핑해서
   → 마치 자기 것처럼 보이지만 사실은 공유하는 것이죠.

🧠 요약 정리

항목	설명
코드 영역 공유 이유	코드(명령어)는 읽기 전용이라 바뀌지 않음
어떻게 공유함?	페이지 테이블을 조작해서 같은 물리 페이지 가리킴
데이터는?	각자 다른 주소 공간을 가짐 (독립적 사용 필요)
효과	메모리 절약 + 실행 속도 향상 (파일 캐싱 덕분에 빠르게 시작 가능)

✅ 비슷한 사례

• 웹브라우저 여러 탭도 공유된 코드 + 독립된 데이터 방식
• 리눅스의 fork()도 처음에는 코드 + 데이터 전부 공유,
  → 이후 데이터가 바뀌면 그때 복사 (Copy-on-Write)

🧠 포인터의 저주와 가비지 컬렉션의 등장 – 메모리를 둘러싼 이야기

1) 💣 포인터는 강력하지만, 매우 위험합니다

C나 C++ 같은 언어를 배우다 보면, 개발자들이 처음 마주하는 메모리의 어두운 세계가 있습니다.
바로 포인터(pointer)입니다.

포인터는 간단히 말하면 “이 변수는 어디에 있습니다”라고 알려주는 주소값입니다.
하지만 문제는, 이 주소도 단순한 숫자라는 점입니다.
모든 숫자가 실제로 존재하는 메모리 주소는 아니기 때문에 주의가 필요합니다.

그렇다면 포인터를 잘못 사용하면 어떤 일이 발생할까요?

🚫 존재하지 않는 메모리에 접근할 경우
→ 프로그램이 강제 종료됩니다.

🚫 CPU의 정렬 조건에 맞지 않는 주소에 접근할 경우
→ 예외가 발생하게 됩니다.

또한 포인터로 메모리를 할당한 뒤에는 반드시 free()를 호출하여 해제해야 합니다.
이 과정을 잊거나 잘못 처리하면 다음과 같은 문제가 발생할 수 있습니다:

• 메모리 누수 (메모리가 회수되지 않고 쌓임)
• 이중 해제 (같은 메모리를 두 번 해제함)
• 해제된 메모리를 참조하는 댕글링 포인터(dangling pointer)

이러한 문제들은 모두 치명적인 오류로 이어질 수 있습니다.

2) 🧹 그래서 등장한 자동 청소 시스템 – 가비지 컬렉션

프로그래머들이 포인터 실수로 어려움을 겪던 시절,
존 매카시(John McCarthy)라는 컴퓨터 과학자가 등장했습니다.

1959년, 그는 LISP라는 언어를 만들면서 메모리 해제를 자동으로 처리하는
가비지 컬렉션(Garbage Collection) 개념을 처음으로 제안하였습니다.

“더 이상 사용하지 않는 메모리는 시스템이 자동으로 정리하자.”
– 존 매카시, 1959년

이로 인해 프로그래머는 free()를 호출하지 않아도 되었고,
보다 안전하게 동적 메모리를 사용할 수 있게 되었습니다.

3) 📦 자바는 포인터 대신 ‘참조’를 사용합니다

자바, 자바스크립트, 파이썬 등 가비지 컬렉션을 사용하는 언어들은
new 연산자를 통해 메모리를 할당하고,
런타임이 자동으로 메모리를 해제해줍니다.

이때 포인터 대신 참조(reference)라는 개념을 사용합니다.
참조는 포인터와 유사한 기능을 하지만,
실제 메모리 주소는 노출되지 않으며
보다 안전하게 객체를 다룰 수 있도록 해줍니다.

4) 🧠 가비지 컬렉션은 어떻게 작동할까요?

가비지 컬렉션의 핵심은 어떤 메모리가 더 이상 사용되지 않는지를 판단하는 것입니다.
대표적인 방식은 다음과 같습니다:

1) 참조 카운팅 (Reference Counting)

• 객체를 참조하는 변수의 개수를 추적합니다.
• 참조 수가 0이 되면 해당 메모리는 해제됩니다.

2) 루트 집합(root set) 기반 추적

• 전역 변수나 스택에 존재하는 변수들을 루트(root)로 설정합니다.
• 이 루트에서 접근 가능한 모든 객체를 탐색하고,
  도달할 수 없는 객체들은 불필요한 메모리로 판단하여 해제합니다.

5) 🤔 하지만 가비지 컬렉션에도 단점이 존재합니다

가비지 컬렉션은 매우 편리한 기능이지만, 다음과 같은 단점도 함께 존재합니다:

항목	설명
❌ 실행 시점 제어 불가	가비지 컬렉션이 언제 실행될지 프로그래머가 제어할 수 없습니다.
❌ 실행 타이밍 문제	중요한 작업 도중에 실행되면 성능 저하가 발생할 수 있습니다.
❌ 불필요한 참조	사용이 끝난 객체가 변수에 참조되어 있으면 GC가 해제하지 못합니다.
❌ 디버깅의 어려움	어떤 객체가 왜 메모리에 남아 있는지 추적하기 어렵습니다.

이로 인해 가비지 컬렉션이 프로그램의 성능을 예측하기 어렵게 만들거나,
메모리 누수를 일으키는 새로운 원인이 되기도 합니다.

구분	포인터 기반 언어 (C/C++)	가비지 컬렉션 언어 (Java 등)
메모리 해제 방식	직접 free() 호출	자동 추적 및 해제
장점	성능 제어가 가능함	메모리 관리가 쉬움
단점	실수로 인한 오류 위험	제어 불가, 성능 예측 어려움
사용 키워드	malloc, free	new, 가비지 컬렉터

메모리 관리는 개발자의 숙명과도 같습니다.

포인터처럼 직접 제어할 수 있는 방식은 정교하지만 위험하고,
가비지 컬렉션처럼 자동화된 방식은 안전하지만 예측이 어려울 수 있습니다.

c언어와 같이 메모리 누수 때문에 생겨난 것이 자바, 그리고 게임 쪽에서는 러스트 입니다.

하지만 가비지 컬렉션을 하게 되면, 메모리를 직접 제어하기는 어렵습니다.

상황과 목적에 따라, 가장 적절한 메모리 관리 방식을 선택하는 것이 중요합니다.

🧹 도시에 쓰레기가 쌓이면 무슨 일이 생길까?

– 가비지 컬렉션(GC)과 JVM 메모리 구조 이야기

1) 🧼 GC는 메모리의 환경미화원이다

여러분도 길을 걷다가 쓰레기가 쌓여 있는 걸 본 적 있으시죠?
그 쓰레기들을 아무도 치우지 않는다면 어떨까요?
당장은 괜찮아 보여도, 시간이 지나면 걷는 것조차 힘들어질지도 몰라요.

이처럼 프로그램이 사용하는 메모리, 특히 힙(Heap)이라는 공간도 마찬가지입니다.
더 이상 사용되지 않는 객체들이 마치 쓰레기처럼 남아 있게 되면
결국 새로운 객체를 위한 공간이 부족해지고, 이때 Out Of Memory Error(OOME)가 발생합니다.

이 쓰레기들을 치우고 메모리 공간을 확보해주는 존재,
그것이 바로 GC(Garbage Collector)입니다.

2) ☕ JVM은 Java 프로그램의 요리사다

JVM, 즉 Java Virtual Machine은 자바 코드를 실행하는 가상의 조리도구입니다.
이 시스템 덕분에 자바는 운영체제(OS)에 종속되지 않고 어느 환경에서나 실행될 수 있어요.

🍳 예를 들어보면?

• 우리는 a1.java, a2.java 같은 Java 소스코드를 작성합니다.
• 이 코드는 컴파일러에 의해 바이트코드(.class 파일)로 바뀌죠.
• 그리고 이 바이트코드를 JVM이 읽고 실행합니다.
  (이때 JVM 안의 인터프리터나 JIT 컴파일러가 작동합니다.)
• Java 인터프리터에 전달된 코드가 실행하기에 적합한 상태인지 확인하는 검증(게이트키퍼)를 거칩니다.
• Java인터프리터를 손상시킬 염려 없이 JVM에서 실행됩니다.

요리 레시피(Java 코드)를 본사에서 작성해 전국 지점에 배포하고,
각 지점의 요리사(JVM)가 자기 주방 환경(OS)에 맞게 요리하는 것과 같습니다.

각 점포의 환경에 영향을 받지 않는다와 같습니다.

그렇다면 컴파일은 어떻게 될까요?

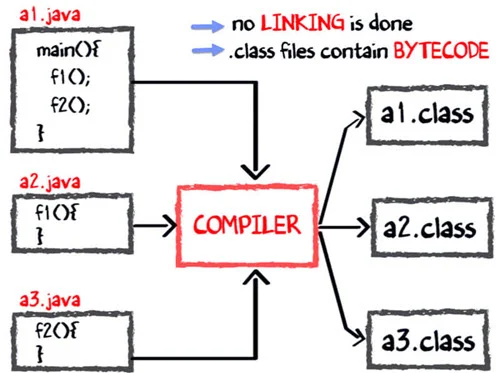
• main 메소드는 a1.java 파일에 저장됩니다.
• 마찬가지로 f1과 f2는 각각 a2.java와 a3.java에 저장합니다.
• 컴파일러는 3개의 파일을 컴파일하여 ByteCode로 구성된 3개의 .class 확장자를 가진 파일을 생성합니다.

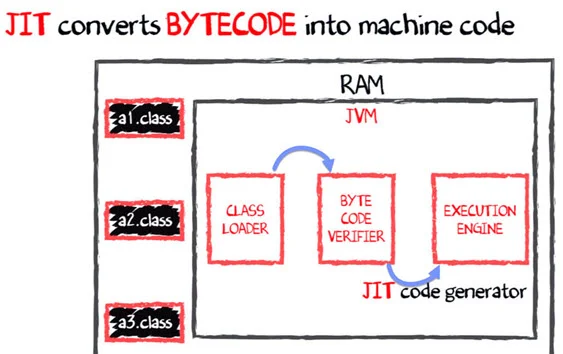
• 이후 RAM에 상주하는 JVM은 클래스 로더를 사용하여 클래스 파일을 RAM으로 가져옵니다.(이때 위에서 설명한 ByteCode Verifier를 거치죠)
• 마지막으로 실행 엔진은 JIT컴파일러 통해 바이트 코드를 네이티브 코드로 변환합니다.

3) 🏗 JVM 아키텍처 구조 한눈에 보기

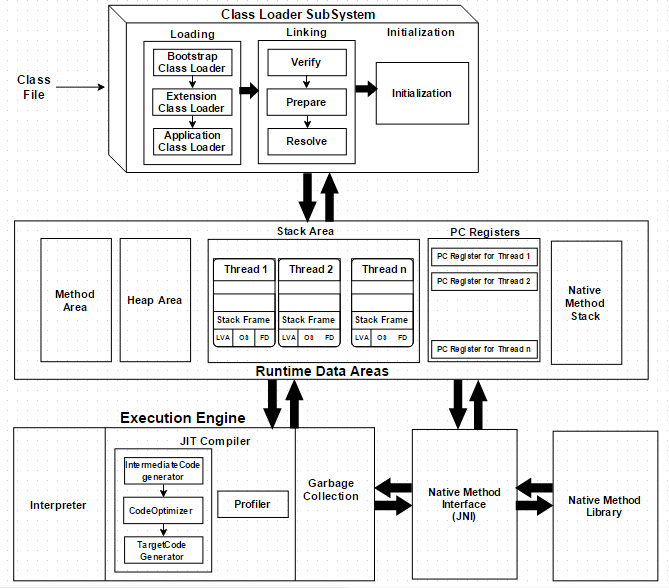
JVM은 크게 3가지 하위 시스템으로 구성돼 있습니다.

구성 요소	설명
Class Loader	Java의 클래스를 런타임에 동적으로 불러옴
Runtime Data Area	코드 실행 중 사용하는 모든 데이터 저장 공간
Execution Engine	바이트코드를 실제 명령어로 변환하고 실행함

Runtime Data Area는 다시 이렇게 나뉘어요:

영역	설명
Method Area	클래스-level 정보와 static 변수 저장
Heap Area	모든 객체, 인스턴스 변수, 배열 저장
Stack Area	각 스레드의 지역변수, 매개변수 저장 (스택 프레임 단위)
PC Register	현재 실행 중인 명령어 위치 저장
Native Method Stack	JVM 외부의 네이티브 코드 정보 저장

4) 🧠 Heap vs Stack – 메모리 구조를 구분하자

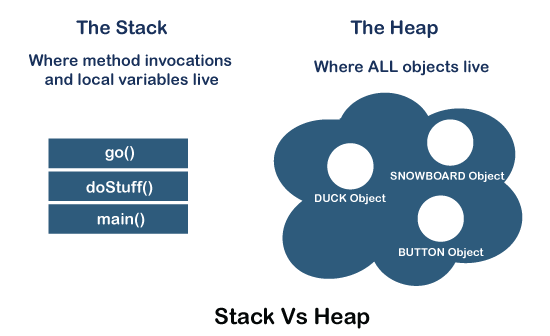
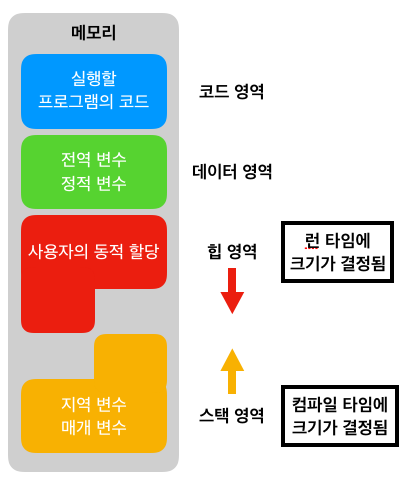
🔹 Stack Memory (스택 메모리)

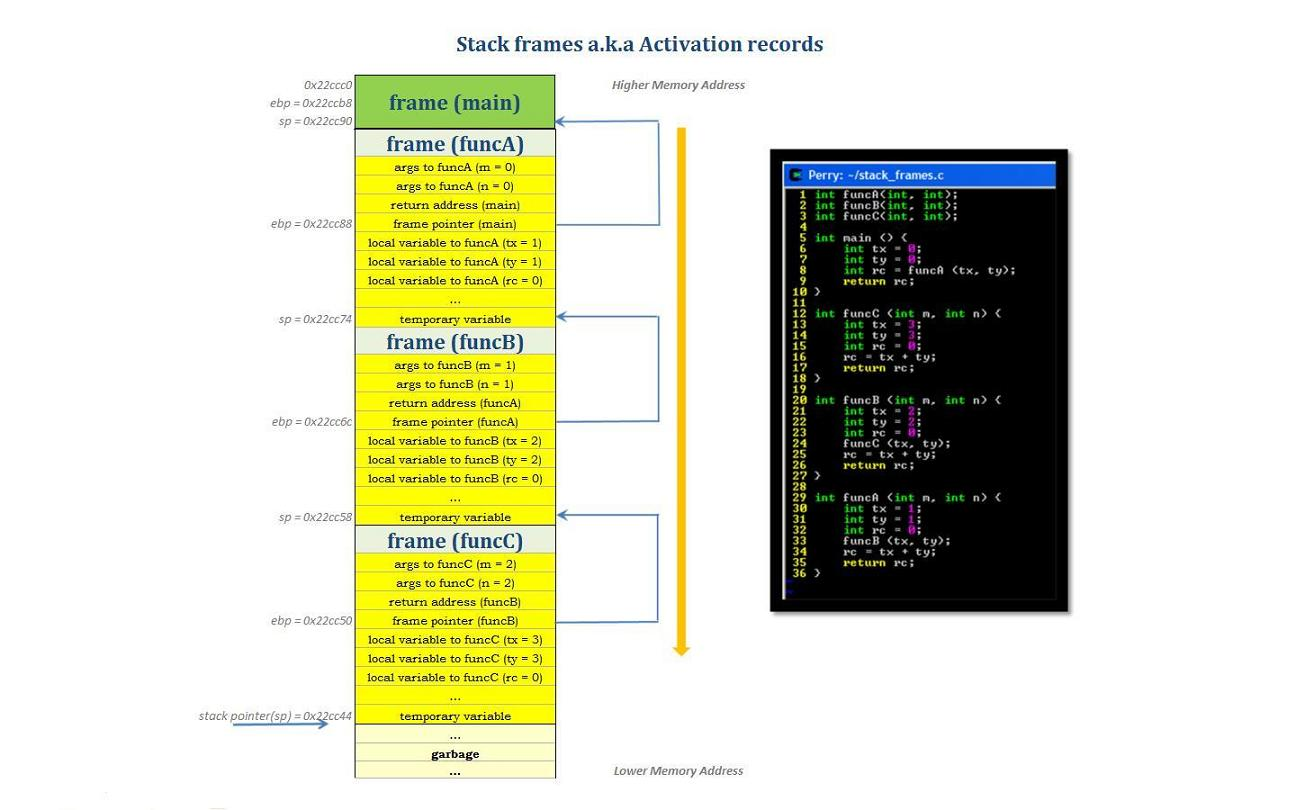
• 각 스레드마다 개별적으로 할당
• 메서드 호출 시 생성되는 매개변수, 지역변수, 반환 주소가 저장됨
• 후입선출(LIFO) 방식으로 작동
• 너무 많이 쌓이면 StackOverflowError 발생

🎬 1. 스레드가 생기면 따라오는 '무대' — 스택

프로그램에서 스레드는 각각 독립적인 흐름을 의미합니다. 마치 연극에서 배우 한 명 한 명이 각자의 대사를 가지고 움직이는 것처럼요.

그리고 이 스레드가 무대 위에 올라서면, 자신만의 무대를 하나 만들어 갖게 됩니다. 바로 스택 메모리(stack memory)입니다.
이 스택 메모리는 컴퓨터의 RAM(주기억장치)에서 각 스레드마다 따로 할당되며, 스레드가 생성될 때 함께 만들어집니다.

즉, 하나의 프로그램 안에 여러 스레드가 있다면, 각각 자신만의 스택 공간을 가지고 있는 셈입니다.
이 덕분에 서로의 무대를 침범하지 않으니, 스레드로부터 안전(thread-safe)하다고 말할 수 있어요.

🎭 2. 함수가 등장할 때마다 생기는 '스택 프레임'

이제 무대 위에서 함수 하나가 호출된다고 상상해볼게요.
그러면 이 함수가 매개변수(parameter), 지역 변수(local variable), 그리고 반환 주소(return address)라는 짐을 들고 무대에 올라옵니다.

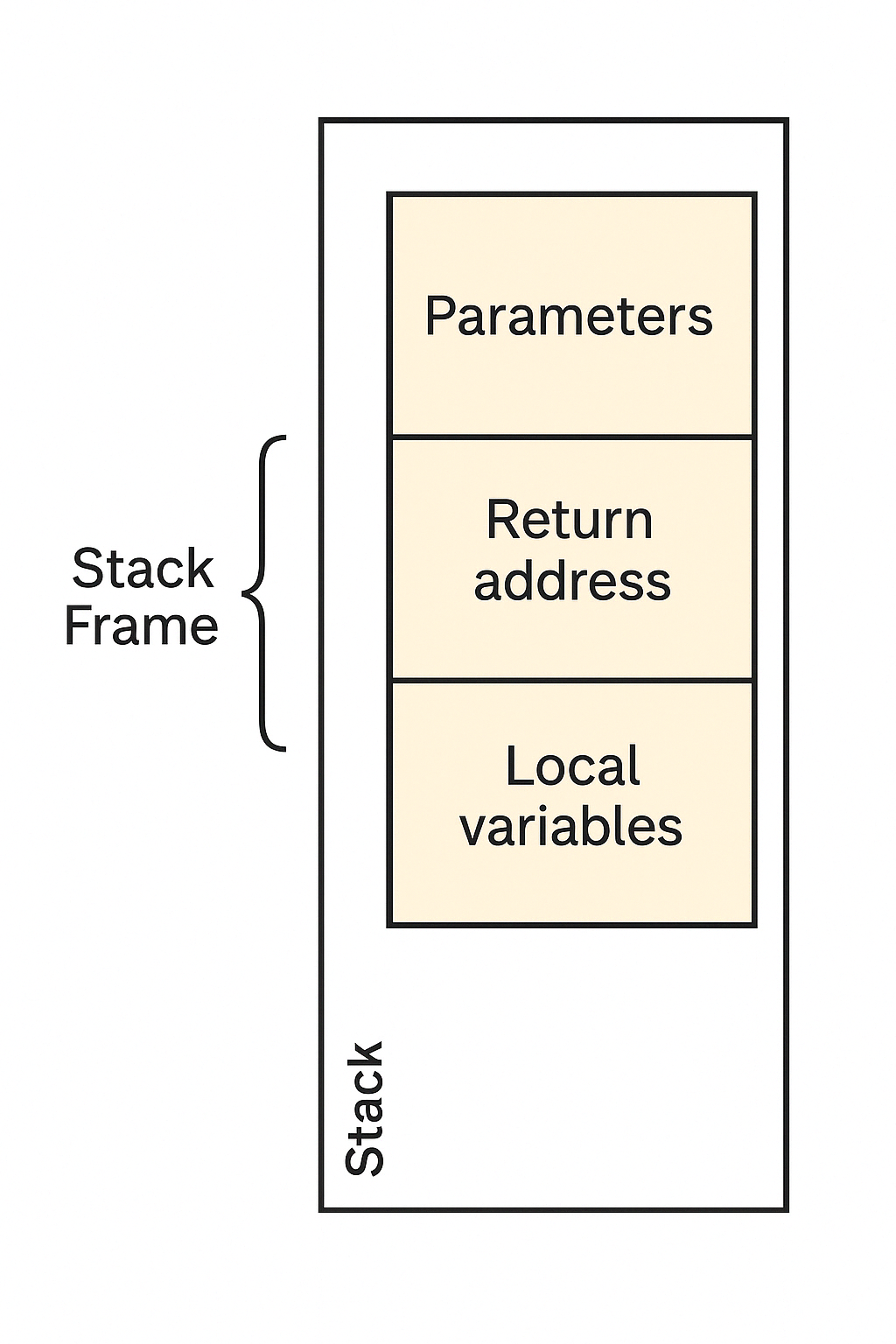
이 짐들은 스택 위에 순서대로 차곡차곡 쌓입니다.
바로 이때 만들어지는 한 덩어리의 공간을 "스택 프레임(Stack Frame)"이라고 부릅니다.

함수 하나가 호출될 때마다 새로운 스택 프레임이 만들어지고,
함수 실행이 끝나면 해당 프레임은 사라집니다.
이렇게 함수 호출의 흐름에 따라 위로 쌓였다가, 끝나면 아래로 사라지는 구조가 바로 "후입선출(LIFO, Last-In-First-Out)"입니다.

📦 3. 스택의 용량은 무한하지 않아요

하지만 이 스택도 무한정 넓은 공간은 아니에요.
정해진 메모리 범위 내에서만 동작하므로, 만약 너무 깊게 함수를 재귀호출하거나, 과도하게 지역 변수를 사용하면 어떻게 될까요?

바로 StackOverflowError라는 오류가 발생하게 됩니다.

이는 우리가 잘 아는 웹사이트 Stack Overflow와는 무관하지만, 이름만큼은 기억하기 좋죠. 😄
이 오류는 스택이라는 무대 위에 더 이상 공간이 없어 배우들이 설 자리를 잃었을 때 발생합니다.

📘 마무리 이야기

스택 메모리는 함수가 호출될 때마다 짧게 등장하는 무대이자, 그 흐름을 가장 가까이서 지켜보는 관객과도 같습니다.
이 무대는 작지만 아주 중요한 역할을 하고 있죠. 함수 하나하나가 연극의 한 장면이라면, 스택 메모리는 그 장면이 자연스럽게 이어지도록 해주는 무대 뒤의 기술팀인 셈입니다.

✅ 스택은 깔끔하고 예측 가능해요!
매번 함수 호출 → 스택 프레임 생성 → 반환되면 자동 해제

🔸 Heap Memory (힙 메모리)

• JVM 시작 시 생성되며 프로그램 전반에 걸쳐 사용
• 객체와 클래스 정보 저장
• GC가 자동으로 정리해줌
• 비동기적으로 작동하므로 스레드 안전성 확보 필요
• 공간 부족 시 OutOfMemoryError 발생

스택이 마치 함수들이 짐을 싸들고 잠깐 머무는 작은 무대라면, 오늘 이야기할 힙 메모리(Heap Memory)는 객체들이 오랫동안 살아가는 공간입니다.

🏡 1. 힙 메모리는 언제 생기고, 누가 쓰나요?

자바 애플리케이션이 실행될 때, JVM이 프로그램을 실행하기 위해 여러 공간을 준비하는데요, 그 중 하나가 바로 이 힙 메모리입니다.

• 힙 메모리는 JVM이 처음 시작될 때 생성되며,
• 프로그램이 종료될 때까지 계속 사용됩니다.

이 공간은 주로 객체(instance)들이 살아가는 곳이에요.
여러분이 new 키워드를 사용해 객체를 생성하면, 그 객체는 바로 힙에 저장됩니다.

그리고 이 객체에 대한 참조(reference)만 스택 메모리에 잠깐 적혀 있게 되죠.
즉, 객체는 힙에 살고, 그 주소는 스택에 남겨진다고 생각하시면 됩니다.

🧭 2. 스택처럼 질서정연하진 않지만...

스택은 후입선출(LIFO) 방식으로 정리정돈이 잘 되어 있는 반면, 힙 메모리는 그런 규칙이 없습니다.
필요한 만큼, 빈 곳이 있으면 어디든지 메모리를 할당합니다. 그래서 ‘Heap’이라는 이름답게, 마치 마당에 물건을 아무데나 쌓아놓은 듯한 구조라고 표현되기도 해요.

하지만 걱정하지 마세요. 자바는 메모리를 잘 관리할 수 있는 시스템을 제공합니다.

🧹 3. 쓰레기 치우는 도우미, GC

객체들이 살다 보면, 더 이상 사용되지 않는 친구들도 생깁니다.
예를 들어, 지역 함수 안에서만 쓰였던 객체는 함수가 끝나면 필요 없어지겠죠?

자바에서는 이런 사용되지 않는 객체들을 자동으로 찾아서 정리해주는 청소부, 즉 GC(Garbage Collector)가 존재합니다.

개발자가 직접 delete 같은 걸 하지 않아도 되기 때문에, 메모리 누수나 오류를 줄일 수 있어요.
단, GC가 작동하는 시점은 예측할 수 없고, 정리할 때는 프로그램 성능에 잠깐 영향을 줄 수도 있습니다.

🔒 4. 스레드에는 안전하지 않아요

스택 메모리는 각 스레드에 독립적으로 존재하기 때문에 서로 간섭이 없습니다.
하지만 힙은 모든 스레드가 공유하는 공간이에요. 그래서 두 개 이상의 스레드가 동시에 힙에 있는 데이터를 수정하려고 하면 문제가 발생할 수 있습니다.

이런 경우를 동기화(synchronization)라고 부르며, synchronized 키워드나 락(lock) 같은 도구를 사용해 데이터 충돌을 방지해야 합니다.

❗ 5. 주의할 점 – 메모리가 꽉 차면?

GC가 있어도, 사용할 수 있는 메모리 공간은 한정되어 있습니다.
객체를 너무 많이 만들거나, 필요 없는 객체를 계속 참조하고 있다면 어떻게 될까요?

바로 OutOfMemoryError가 발생합니다.
말 그대로, 더 이상 저장할 공간이 없다는 뜻이죠.

이런 문제를 피하려면, 사용하지 않는 객체의 참조를 null로 바꾸거나, 컬렉션 객체를 잘 관리해주는 것이 중요합니다.

💡 마무리 이야기

힙 메모리는 마치 객체들의 장기 숙소 같다고 볼 수 있습니다.
객체들이 자유롭게 이곳에 머물 수 있도록, 자바는 GC라는 청소부도 고용하고, 적절한 동기화로 질서도 잡아주죠.

하지만 이 공간 역시 한정된 리소스이기 때문에, 개발자의 올바른 설계와 메모리 관리 습관이 무엇보다 중요합니다.

객체들이 편안하게 잘 지낼 수 있도록, 우리는 좋은 집주인이 되어야 합니다 😊

✅ 힙은 자유롭지만 관리가 필요해요.
객체 생성은 쉽지만, 삭제는 GC의 몫입니다.

5) 🧼 GC는 언제, 어떻게 쓰레기를 치울까?

GC는 힙 메모리 안의 사용되지 않는 객체들을 감지해 자동으로 제거합니다.
다만, GC가 언제 작동할지 명확하게 제어할 수는 없고,
System.gc()로 요청할 수는 있지만, 실행 여부는 JVM이 판단합니다.

GC를 구성하는 여러 알고리즘들(Mark & Sweep, G1, CMS 등)은
뒤에서 더 깊게 다룰 수 있어요. 기본적으로는 다음 흐름을 기억해두세요:

객체 생성 → 참조 해제 → GC 감지 → 정리

항목	Stack Memory	Heap Memory
저장 대상	매개변수, 지역변수	객체, 배열
관리 주체	자동으로 스택 프레임 생성/소멸	GC에 의해 자동 관리
스레드 안전성	스레드별 분리 → 안전함	동기화 필요
오류 예시	StackOverflowError	OutOfMemoryError

• 출처 : JVM과 GC 그리고 GC튜닝 연습까지

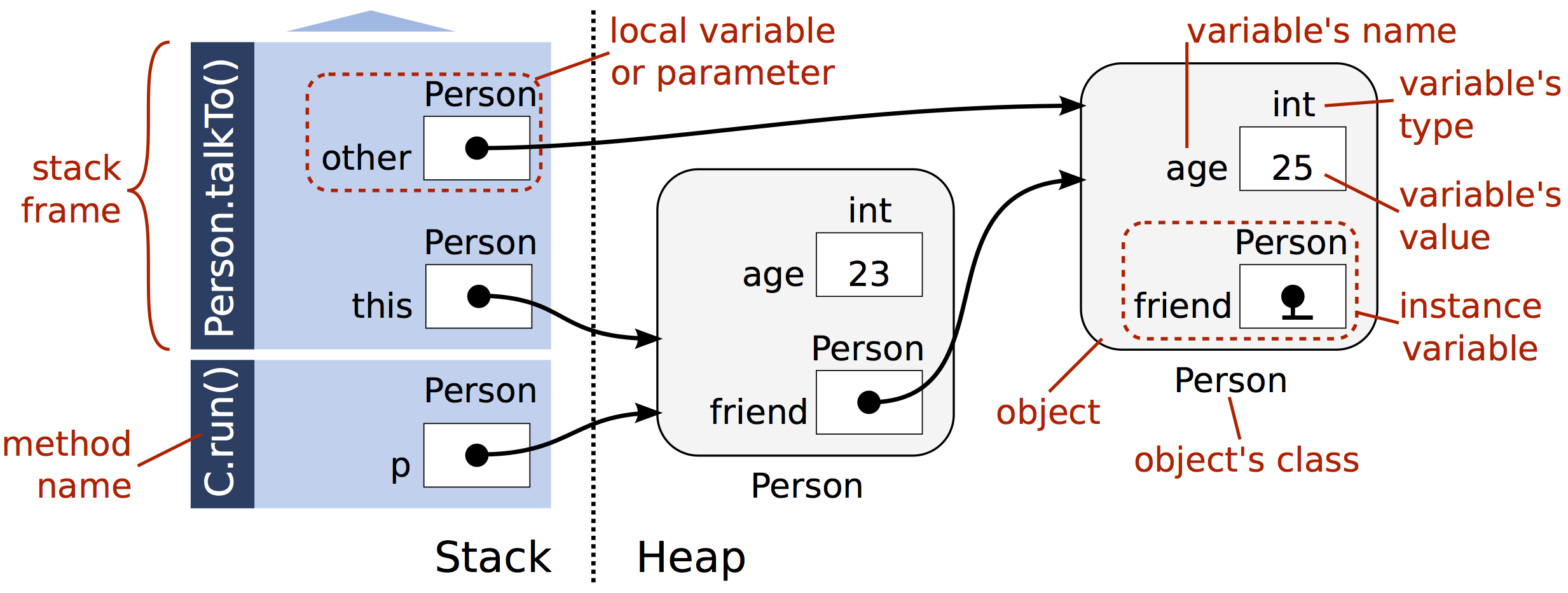
6) JVM이 만든 두 도시: Stack vs Heap

프로그램이 실행되면, JVM은 두 개의 도시를 만듭니다.
하나는 Stack, 짧고 강렬한 함수들이 잠시 머무는 곳.
다른 하나는 Heap, 객체들이 비교적 오래 살아가는 넓은 땅입니다.

이 중에서 오늘은 Heap Memory를 중심으로, 객체들의 탄생과 소멸, 그리고 그들을 정리하는 GC(Garbage Collector)의 여정을 따라가 보려 합니다.

Heap Memory 내부: 세대 구분이 있는 세계

👶 Young Generation (젊은 세대)

새로 태어난 객체는 무조건 이곳, Eden이라는 공간에 도착합니다.
하지만 이곳은 공간이 협소해서 곧 꽉 차버리죠.

• Eden이 가득 차면? Minor GC(또는 Scavenge GC)가 동작합니다.
• 사용되지 않는 객체는 즉시 삭제, 살아남은 객체는 S1(Survivor Space)로 이동합니다.
• 다음 GC 때는 S1 → S2로, 다시 그 다음에는 S2 → S1로… 공간을 번갈아 사용합니다.
• 이 과정을 여러 번 버틴 객체는 “어이, 오래 살았으니 이사 가세요~”라는 말을 듣고 Old Generation으로 이동하게 됩니다.

💡 JVM 옵션으로 Young 영역의 비율도 조절할 수 있어요.
예: -XX:SurvivorRatio=6 → Eden : S1 : S2 = 6 : 1 : 1

👴 Old Generation (구 세대)

Young Generation에서 살아남은 객체들이 이사 온 공간입니다.

• 이곳에선 Major GC가 발생하고,
• 전체 Heap 중 많은 비율을 차지하며,
• GC가 발생하면 정말 오래 멈추는 경우도 생깁니다.

참고: Young + Old 모두 정리하는 GC는 Full GC라고 합니다.

🧾 Metaspace (구 PermGen)

자바 8 이전에는 PermGen이라는 공간이 있었는데, 이는 클래스 메타데이터를 Heap 안에 저장하던 영역이었습니다.
하지만 자바 8부터는 이걸 Heap 밖으로 꺼내서 OS가 관리하도록 바꿨습니다.
이 공간을 Metaspace라고 합니다. Heap은 JVM에서 관리합니다.

🧽 JVM 속 작은 마을의 이사 이야기 — 객체의 생존과 GC 순환 과정

JVM 안에는 객체들이 태어나서 자라고, 이사를 가고, 사라지는 작은 마을이 있습니다.
이 마을에는 Eden, Survivor(S0/S1), Old Generation이라는 동네들이 존재하죠.
이제 막 태어난 객체가 어떻게 이 마을을 이리저리 옮겨 다니는지를 하나씩 따라가 볼까요?

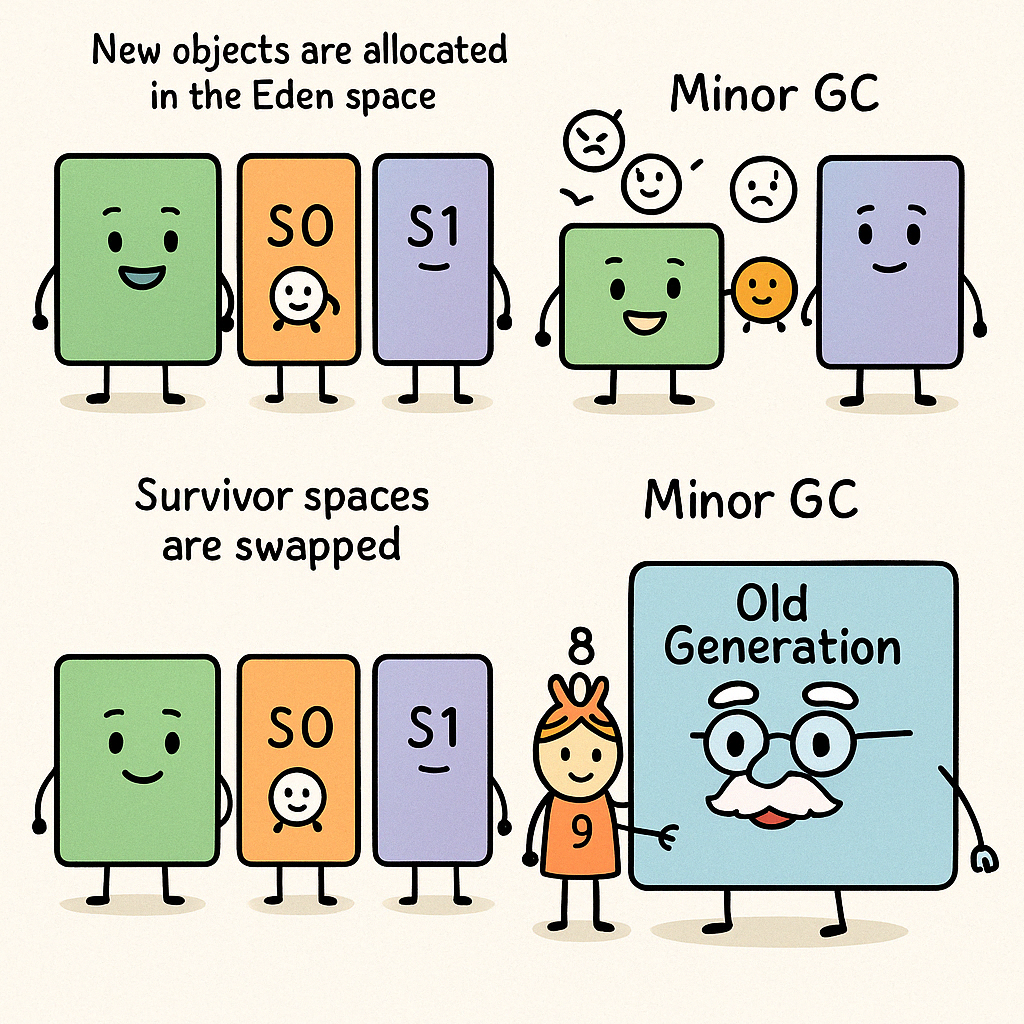
🌱 1단계: 객체는 Eden에 태어난다

모든 새 객체는 무조건 Eden이라는 구역에 태어납니다.
Eden은 Young Generation 안의 한 공간으로, 젊고 새로운 객체들이 살기 좋은 동네예요.

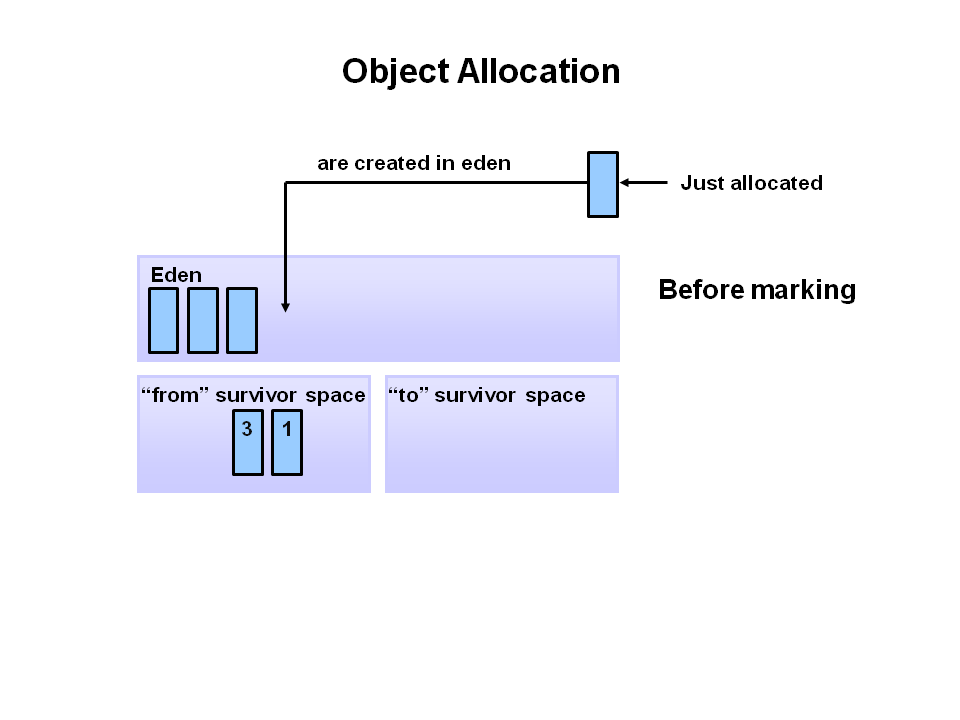
하지만 이 동네는 좁기 때문에, 곧 가득 차게 됩니다.

🔄 2단계: Eden이 꽉 차면 Minor GC가 등장한다

Eden에 공간이 없어지면, 청소부 GC가 등장합니다.
이 GC를 우리는 Minor GC라고 부릅니다.

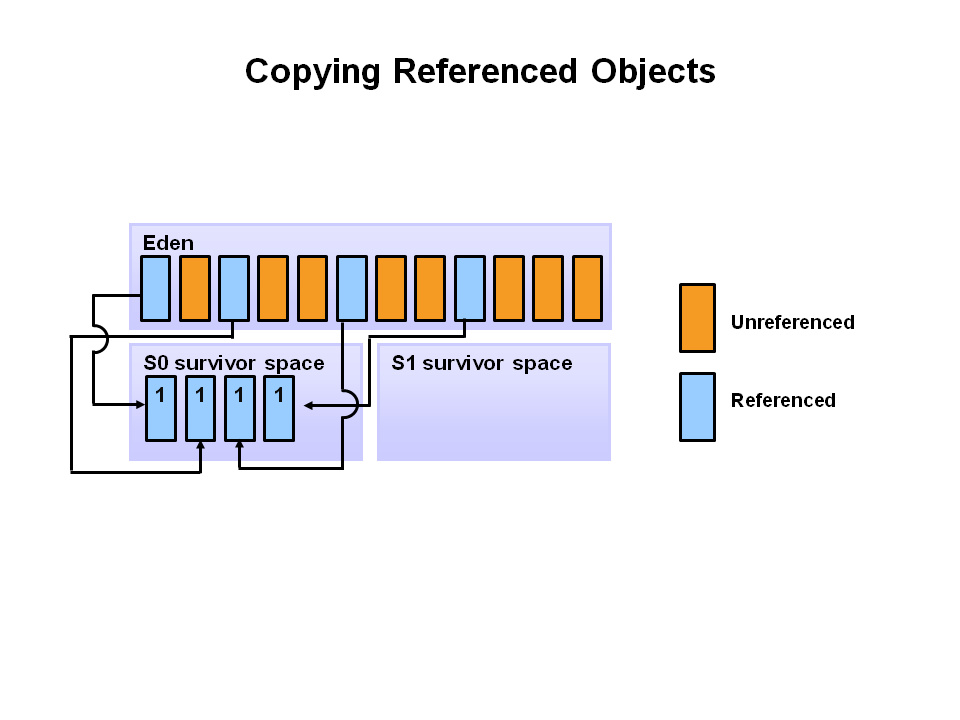
• 참조되지 않는 객체들은 “이제 필요 없어졌어”라는 판정을 받고 삭제됩니다.
• 살아남은 객체들은 잠시 머무는 임시 거처인 Survivor 공간 S0(Survivor 0)으로 이사하게 됩니다.

Eden은 완전히 비워지고, S0에 생존자만 남게 되죠.

🔁 3단계: 다음 GC 때 S1으로 이동

이후 또다시 Eden에 새 객체들이 태어나고, 시간이 흐르면 Eden은 또 가득 찹니다.
그리고 다시 Minor GC가 작동하게 되죠.

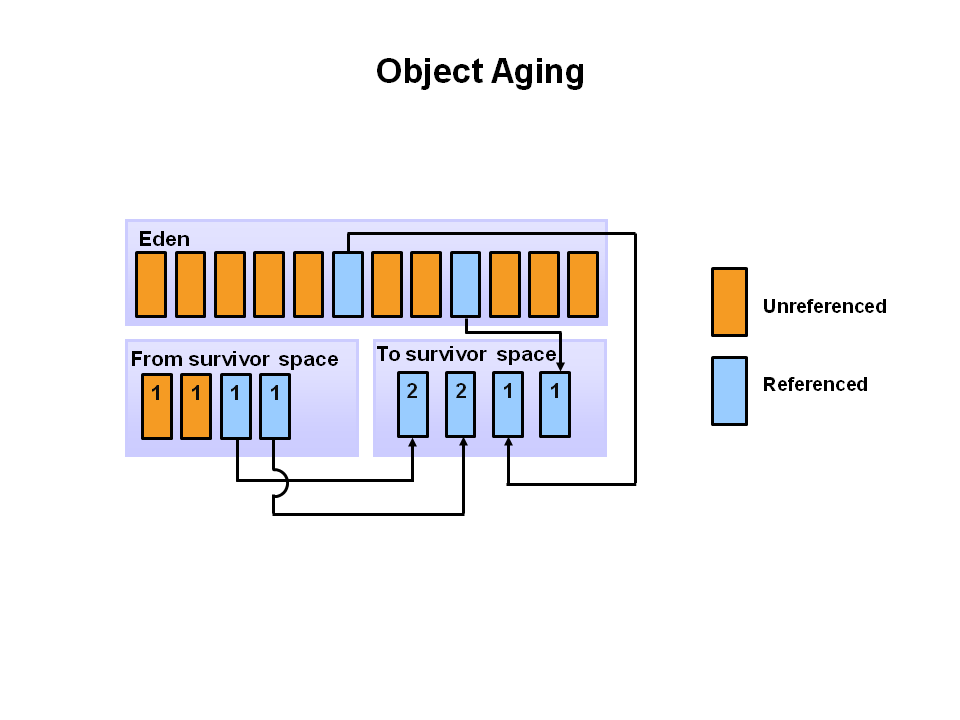
• 새로 태어난 객체 중 살아남은 애들은 이번엔 S1(Survivor 1)으로 이사합니다.
• 이전 S0에 있던 객체들도 나이를 한 살 더 먹고, 같이 S1으로 이사하게 됩니다.

이때 S0와 Eden은 비워지고 삭제됩니다.
S1에는 두 번의 GC를 살아남은 객체들이 모여있습니다.

🔁 4단계: GC는 계속되고 공간은 번갈아 사용된다

이후 Minor GC가 반복되면,
S1 → S0로, 다시 S0 → S1로 번갈아가며 객체들이 이동하게 됩니다.

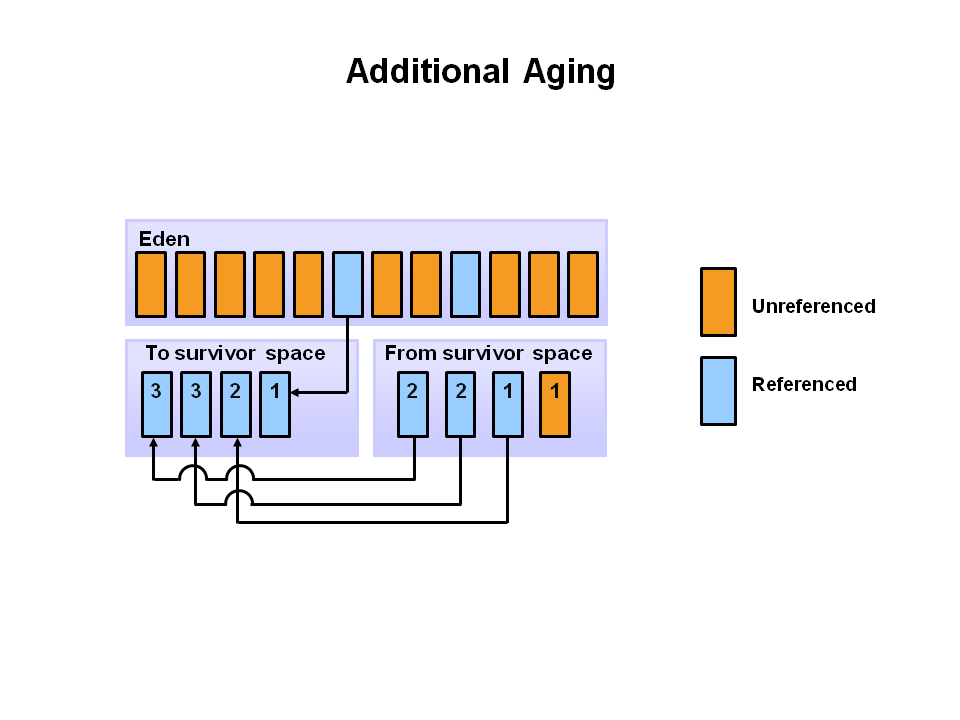
매번 살아남은 객체들만 다른 쪽 Survivor 공간으로 이동하며,
사용된 Survivor 공간과 Eden은 삭제됩니다.

🧓 5단계: 오래 살아남은 객체는 Old로 이사

Survivor 공간을 여러 번(보통 8번) 넘나들면서 생존한 객체는, 이제 이 마을의 장기 거주자가 되었다는 뜻입니다.
이제는 Young Generation이 아니라, 좀 더 넓고 오래 머물 수 있는 Old Generation으로 이사하게 됩니다.

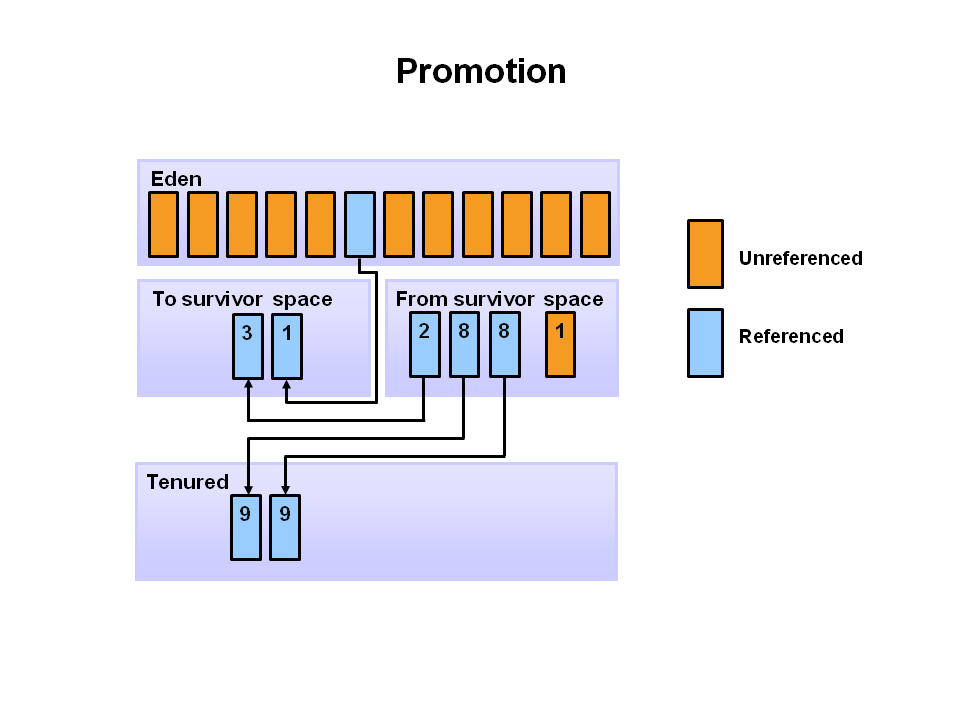
이러한 객체를 JVM에서는 “Promotion 됐다”고 표현해요.

이 임계값은 JVM에 따라 다르지만 기본적으로 8살이 되면 이사를 갑니다.

🧼 6단계: Old Generation에서 Major GC 발생

Old Generation에 있는 객체들은 잘 지워지지 않습니다.
그러다 보니 공간이 점점 차게 되고,
이때 등장하는 것이 바로 Major GC입니다.

• 이 GC는 Young보다 훨씬 무겁고, 오래 멈춥니다.
• 오래 살아남은 객체들도 이때 비로소 정리되고,
• 메모리는 다시 사용 가능해집니다.

🔁 전체 순환 요약

단계	공간	내용
1	Eden	새 객체 생성
2	Minor GC	Eden이 가득 차면, 생존자는 S0으로, 나머지는 삭제
3	Minor GC 반복	Eden → S1, S0도 함께 S1로 이사. S0 & Eden 삭제
4	계속 반복	S0 ⇄ S1 번갈아가며 생존자 이동
5	Promotion	일정 생존 횟수 초과 시 Old Generation으로 이사
6	Major GC	Old Generation이 꽉 차면 오래된 객체를 정리

🧠 마무리 정리

이처럼 JVM의 객체는 단순히 생기고 없어지는 것이 아니라,
나이에 따라 이사하고, 살아남으면 더 넓은 집으로 옮겨갑니다.
이 흐름을 이해하면, GC 튜닝이나 성능 이슈를 해결할 때 매우 유용합니다!

GC는 단순한 기술이 아니라, JVM이 ‘어떤 객체를 오래 살릴지, 어떻게 빨리 치울지’를 고민한 결과물이에요 😊

GC Alogorithm

✅ Reference Counting (참조 카운트)

• 객체가 몇 개의 참조를 받고 있는지를 세어 저장합니다.
• 참조 수가 0이 되면 “더 이상 이 객체는 필요 없어요!” 라고 판단해 삭제합니다.

✔ 빠르지만 순환 참조는 못 지워요 → Memory Leak 위험

✅ Mark and Sweep

1. Mark 단계: 살아있는 객체에 표시를 합니다.
2. Sweep 단계: 표시되지 않은 객체는 메모리에서 제거합니다.

✔ 순환참조도 OK
❌ 메모리 단편화 발생 → 파편처럼 빈 공간이 남아요

✅ Mark-Sweep-Compact

• 위 방식에서 살아남은 객체들을 앞으로 당겨서 정리합니다.
• 이 과정이 바로 Compaction입니다.

✔ 단편화 해결
❌ 이동 + 참조 업데이트 비용 발생 → GC 일시중지 시간 증가

✅ Copying

• 메모리를 절반으로 나눠 사용합니다.
• 살아남은 객체를 다른 쪽 공간으로 복사(Copy)한 뒤, 남은 공간은 통째로 비웁니다.

✔ 단순한 구조
❌ 힙의 절반만 사용 → 공간 낭비, 복사 오버헤드 있음

✅ Generational GC (현대 GC 구조)

Weak Generational Hypothesis에 기반한 전략입니다:

• 대부분 객체는 오래 살지 않으며
• 오래된 객체가 젊은 객체를 참조할 일도 드뭅니다.

그래서 Young, Old 세대로 나누어 GC를 효율적으로 수행합니다.
→ 우리가 위에서 본 Eden, S1, S2, Old는 이 전략에 딱 맞춰 구성된 거예요!

GC 수집기들 – JVM의 청소팀

☕ Java 7 & 8 – Parallel GC

• 여러 스레드가 동시에 GC를 수행합니다.
• 옵션: -XX:+UseParallelGC
• Old 영역도 함께 관리하려면: -XX:+UseParallelOldGC

🧠 Java 9 ~ 11 – G1 GC

• Heap을 고정 세대가 아닌 동일 크기의 Region으로 나눕니다.
• Garbage가 많은 Region부터 청소 → 그래서 이름이 Garbage First (G1)

단계:
1. Initial Mark (STW)
2. Root Region Scan
3. Concurrent Mark
4. Remark (STW)
5. Cleanup (STW)
6. Copy

✔ 대용량 Heap에 적합, Stop-the-world 최소화
❌ 압축 시 일시 중지 발생 가능

⚡ Java 15~Now – ZGC (1ms 미만 STW 목표)

• 동시성 기반 GC, 대부분의 작업을 애플리케이션과 함께 수행합니다.
• 메모리 재배치도 STW 없이 진행!
• Load barriers와 Colored pointers라는 기술로 포인터 추적도 동시성 있게!

✔ 1ms 미만의 정해진 STW 시간
✔ 큰 Heap에서도 효율적
✔ 세대형(G1처럼 Young/Old 구분) 기능까지 추가됨 (Generational ZGC)

📌 요약 표 – JVM GC 정리

구분	영역	GC 유형	주요 특징
Eden	Young	Minor GC	새 객체 생성, 가장 자주 GC
S1/S2	Young	Minor GC	살아남은 객체 임시 이동 공간
Old	Old	Major GC	오래된 객체, 압축 정리
Metaspace	Native	-	클래스 메타 저장, JVM 외 관리
Full GC	전체	Full	Minor + Major 동시 수행
ZGC	전체	Concurrent	고성능, 짧은 일시 중지, Generational 포함

JVM에서의 메모리 관리는 마치 청소가 철저한 아파트 단지와도 같습니다.
객체는 새 집에 입주하고, 일정 시간 살다가, 안 쓰이면 청소부 GC가 나와서 정리합니다.

그리고 이 청소부들은 점점 더 똑똑해져서, 청소도 조용히 하고, 다른 주민들(애플리케이션 실행)에게 방해되지 않도록 노력하고 있죠.

GC 튜닝도 가능해요!

• 가비지 컬렉션 gc 튜닝 절차

하지만 주의해야 할 것이 있습니다. 🧹 GC 튜닝, 그거 진짜 먼저 해도 될까?를 생각해 봐야 해요. 가비지 컬렉션을 다루기 전에 꼭 생각해야 할 두 가지 이야기

1. “남이 했다고 우리도 따라 해도 될까?”

자, 여러분. 누군가가 이렇게 말하는 걸 들어본 적 있을 거예요.

“이 GC 옵션 쓰니까 성능이 쭉쭉 나와요!”
“그럼 우리도 저 설정 그대로 넣어볼까?”

이렇게 성공 사례를 그대로 따라 하려는 유혹이 생기곤 하죠.
하지만 이건 절대 금물입니다.

왜냐고요?

서비스마다 동작 방식도, 처리하는 데이터도, 생성하는 객체의 크기나 수명도 모두 다르기 때문이에요.
예를 들어 어떤 서비스는 잠깐 쓰고 버리는 객체가 많고,
어떤 서비스는 오래 살아 있는 대형 객체가 많아요.

그래서 GC 옵션도 상황 따라 전혀 다르게 튜닝되어야 합니다.
결국 정답은 하나가 아니라, 우리 서비스만의 GC 패턴을 직접 파악해야 해요.

✅ “모니터링 없이 GC 튜닝은 없다.”
→ GC 로그, 메트릭을 보고 정확히 STW(Stop The World)가 언제, 어디서 일어나는지 확인해야 합니다.

2. “GC 튜닝은 마지막에 해야 하는 작업입니다”

개발자들 사이에 이런 말이 있어요.

“GC는 마지막에 건드려라.”

왜일까요?

GC 튜닝은 사실 얻는 것에 비해 신경 써야 할 게 너무 많기 때문입니다.

• GC 동작 방식 이해해야죠
• JVM 옵션별 차이 알아야죠
• 로그 분석도 해야죠

이렇게 손이 많이 가는 작업인데,
실제 성능 개선은 그리 크지 않을 수도 있습니다.

오히려 먼저 해야 할 것은 무엇일까요?

👉 “불필요한 객체 생성을 줄이는 리팩토링”입니다.

💡 근본적인 해결책: 코드에서 객체 생성을 줄이자

자바의 가비지 컬렉터는 우리가 만든 객체들을 모아서 정리하는 청소부예요.
그런데 생성된 객체가 많으면 많을수록 GC가 청소해야 할 양도 늘어나고,
GC 실행도 자주 하게 되니 결국 STW도 많아지고 성능이 떨어지게 되는 것이죠.

그러니 이 문제를 GC 설정으로 덮으려 하지 말고,
애초에 쓰레기를 덜 만들자!는 전략이 더 낫습니다.

🎯 예를 들어 이런 것부터 리팩토링해보세요:

• String 객체를 자꾸 이어붙이지 말고 → StringBuilder나 StringBuffer 사용하기
• 불필요한 log.debug() 호출 줄이기
• 루프 내에서 반복 객체 생성 줄이기
• 불필요한 Map, List 생성 피하기

이런 방식으로 애플리케이션 코드 레벨에서 메모리를 줄이는 것이
GC 튜닝보다 훨씬 더 효과적인 시작점이 됩니다.

✅ 그리고 마지막으로, 진짜 문제가 남아있을 때

코드 최적화도 하고, 리팩토링도 다 했는데도
아직도 STW나 GC pause가 문제라면…

그때가 바로 GC 튜닝을 고려해볼 시점입니다.

GC 튜닝은 자바 성능 개선 작업의 ‘최종 병기’입니다.
그전에 코드에서 불필요한 객체 생성을 줄이는 것이 진짜 해결책입니다.

• 출처: https://inpa.tistory.com/entry/JAVA-☕-가비지-컬렉션-GC-튜닝-맛보기 [Inpa Dev 👨‍💻:티스토리]

🌳 선형을 넘어서: 2진 트리(Binary Tree) 구조의 세계

1) 선형 구조의 한계

지금까지 우리는 배열, 연결 리스트와 같은 선형 데이터 구조(linear data structure)를 배워왔어요.
이 구조들은 단순하고 효율적이지만, 데이터가 많아질수록 성능에 한계가 생깁니다.

예를 들어 연결 리스트에서 특정 값을 찾으려면?

• 하나씩 순차적으로 탐색해야 하죠.
• 최악의 경우 n개의 데이터를 모두 탐색해야 해요.
  → 시간 복잡도: O(n)

👉 그래서 "더 효율적으로 검색하고 싶다!"는 욕구가 생깁니다.

2) 트리(Tree): 계층적 구조의 등장

연결 리스트에서는 각 노드가 1개의 다음 노드만 가리키지만,
트리 구조에서는 노드가 여러 노드를 가리킬 수 있어요.

그중에서도 가장 단순하고 많이 쓰이는 구조가 바로 2진 트리(Binary Tree)입니다.

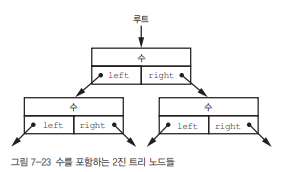
✅ '2진'이란?
각 노드가 최대 2개의 자식 노드(왼쪽, 오른쪽)를 가질 수 있다는 뜻입니다.

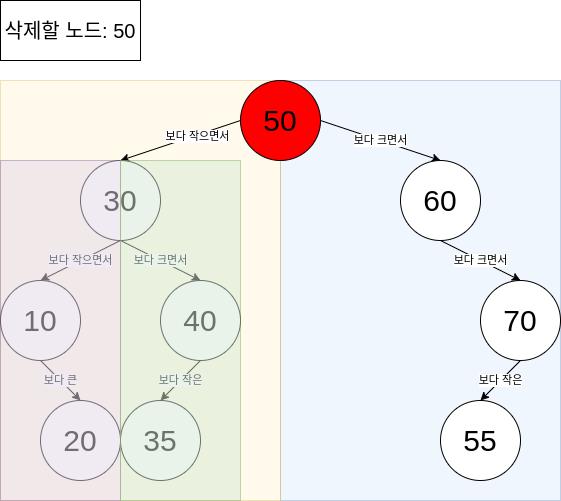
3) 2진 트리 삽입 알고리즘 – 숫자 빙고 예시로 이해하기

예를 들어, 우리는 빙고 게임에서 나온 숫자를 2진 트리에 저장하고 싶습니다.

삽입 규칙은 다음과 같아요:

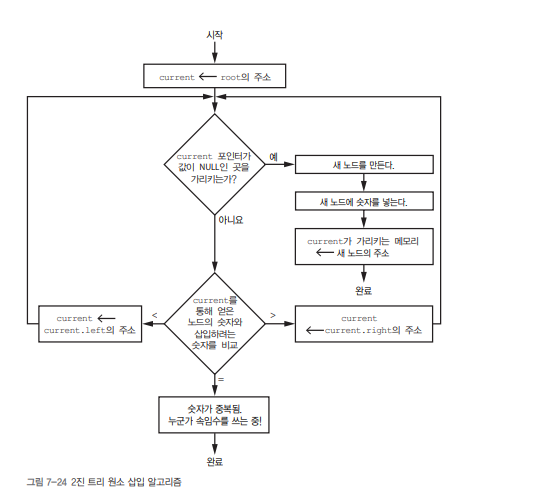
1. 트리의 루트(root)는 첫 번째 값이 됩니다.
2. 새 값을 기존 노드와 비교합니다:
   • 작으면 왼쪽(left)
   • 크면 오른쪽(right)
3. 이동한 곳이 비어 있으면 그곳에 새 노드를 생성합니다.
4. 중복된 값이 있으면? ❗ "누군가 속임수를 쓰고 있어요!"

🎲 예시: 순서대로 숫자를 삽입해볼게요

삽입 순서: 8 → 6 → 9 → 4 → 7

숫자	비교 경로	결과 위치
8	없음 (루트 없음)	루트
6	8보다 작음	8의 왼쪽
9	8보다 큼	8의 오른쪽
4	8 > 6 > 4	6의 왼쪽
7	8 > 6 < 7	6의 오른쪽

📌 이렇게 하면 최종 트리는 아래와 같아요:

✅ 삽입 시마다 노드를 비교하며, 새 위치를 찾기 위해 내려가는 구조입니다.

4) 검색 알고리즘: 원하는 숫자 찾기

검색은 삽입보다 더 간단합니다.

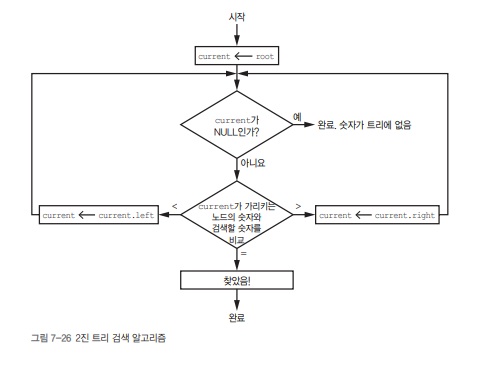
1. 루트부터 시작해서 현재 노드와 찾고자 하는 숫자를 비교
2. 같으면 찾기 성공
3. 작으면 왼쪽, 크면 오른쪽으로 이동
4. NULL이 되면 트리에 값이 없는 것!

이 과정은 트리를 변형하지 않고 단순히 비교만 반복하기 때문에 더 빠릅니다.

5) 트리의 모양이 성능을 좌우한다!

❗ 문제는 삽입 순서에 따라 "트리 모양이 달라진다"는 점입니다.

예를 들어 4 → 5 → 6 → 8 → 9 순으로 삽입하면?

4
 \
  5
   \
    6
     \
      8
       \
        9

이건 연결 리스트랑 똑같은 모양이에요.
→ 검색 효율 O(n)으로 다시 퇴화합니다.

6) 트리의 균형 (Balancing)의 중요성

균형 잡힌 트리(Balanced Tree)는 깊이가 최소화되어 있어
검색/삽입 성능이 탁월해요.

• 연결 리스트: 최대 n번 비교
• 균형 이진 트리: log₂n번 비교

예: 데이터가 1,024개일 때

• 연결 리스트: 1,024번 비교
• 균형 트리: 10번이면 충분!

7) 균형 유지 알고리즘의 등장

• 대표적으로 AVL 트리, Red-Black Tree, B-Tree 등이 있어요.
• 하지만 트리를 균형 잡으려면 삽입, 삭제 시 추가 연산이 필요합니다.
• 균형 유지는 시간과 공간의 비용이 들지만,
• 커진 데이터에서의 검색 성능 향상으로 그 비용을 상쇄합니다.

📌 핵심 요약

개념	설명
선형 구조	배열, 연결 리스트 – 삽입은 빠르나 검색은 느림 (O(n))
2진 트리	노드당 최대 2개의 자식 노드 – 계층적 구조
삽입	값 비교 후 왼쪽/오른쪽 자식으로 이동하며 노드 삽입
검색	루트부터 값 비교 – 트리 깊이만큼 비교 (최대 O(log n))
트리의 모양	삽입 순서에 따라 트리의 성능이 크게 달라짐
균형 트리	log₂n 성능 보장 – 데이터가 많을수록 유리
균형 유지 비용	삽입/삭제 시 추가 연산이 필요함 (trade-off 존재)

🌟 연결 리스트는 ‘단순함’이 장점이고,
🌲 2진 트리는 ‘빠른 탐색’이 무기입니다.
대용량 데이터를 다룬다면, 트리를 잘 쓰는 것이 성능 향상의 지름길이에요!

균형 이진 트리와 불균형 트리의 탐색

균형 이진 트리의 검색 시간은 O(1)이 아니라 O(log N)이고,불균형 트리는 최악의 경우 O(N)

🎯 1. "탐색 성능 = 트리의 깊이"

트리 구조에서 검색(Search)을 한다는 건,
루트부터 시작해서 왼쪽, 오른쪽 자식 노드를 따라 내려가며 비교하는 작업이에요.

즉, "몇 번 내려가야 원하는 값을 찾을 수 있느냐?" = 탐색 시간입니다.

🌲 2. 균형 이진 트리 vs 불균형 트리 구조

✅ 균형 이진 트리 (Balanced Binary Tree)

• 각 노드의 왼쪽과 오른쪽 서브트리의 높이 차이가 거의 없음
• 즉, 트리가 완만하게 분산되어 있음
• 예를 들어, 노드가 1,024개면?
  → 트리의 깊이는 약 log₂(1024) = 10단계만에 탐색 가능

따라서 시간 복잡도는: O(log N)
❗ O(1)은 아닙니다! (그건 해시 테이블 같은 자료구조에서 가능한 성능이에요.)

❌ 불균형 이진 트리 (Skewed Tree)

• 모든 노드가 한쪽(예: 오른쪽)에만 자식을 가지고 있음
• 즉, 트리 모양이 거의 연결 리스트처럼 됨

예시:

1
 \
  2
   \
    3
     \
      4

• 이 경우 값을 찾기 위해서는 맨 아래까지 전부 탐색해야 함
  → 시간 복잡도: O(N)

🧠 3. 숫자로 비교해보면?

노드 수 N	균형 트리 (log₂N)	불균형 트리 (최대 탐색 횟수)
1,000	약 10	최대 1,000번 비교
1,000,000	약 20	최대 1,000,000번 비교

📌 균형만 잘 잡으면 탐색 횟수를 압도적으로 줄일 수 있어요!

구조	깊이	탐색 시간 복잡도	특징
균형 이진 트리	log₂N	O(log N)	대부분의 노드가 고르게 퍼져 있어 탐색이 빠름
불균형 트리	최대 N	O(N)	한쪽으로 치우쳐져 탐색 성능이 급격히 나빠짐

🌳 트리는 단순히 “2개로 갈라지는 구조”가 아니라,
"얼마나 균형 있게 갈라지느냐"에 따라 탐색 성능이 완전히 달라지는 구조예요!

4. 균형 이진 트리 왜 이렇게 빠른가요?

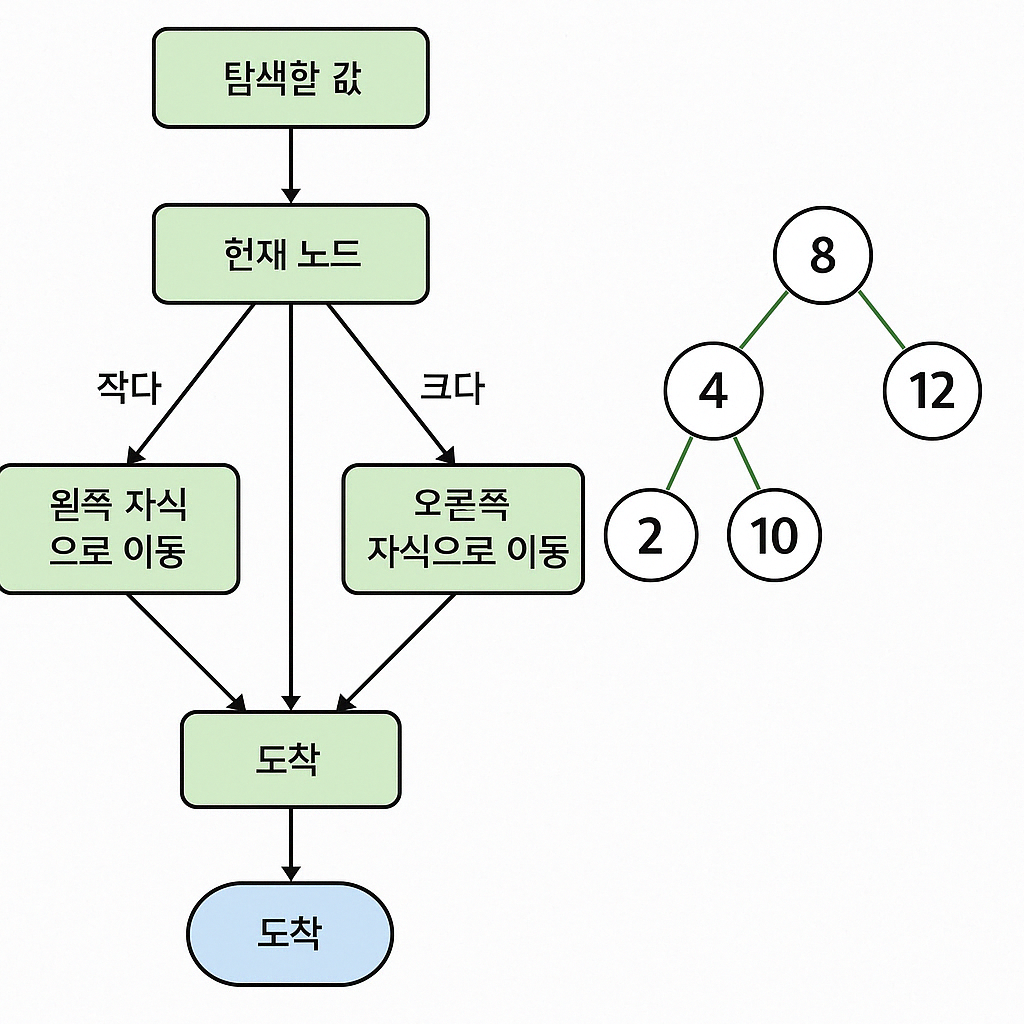
비결은 "한 번 비교할 때마다 후보군이 절반으로 줄어들기 때문"입니다.

• 처음 8과 비교했을 때, 전체 7개 노드 중 절반(왼쪽 or 오른쪽)만 남습니다.
• 다음 12와 비교하면 또 절반이 줄어요.
• 이렇게 계속 나누다 보면 금방 원하는 값을 찾게 됩니다.

📚 검색 횟수 ≈ 트리의 깊이 ≈ log₂(N)
그래서 탐색 시간 복잡도가 O(log N)이 되는 거예요.

5. 균형 이진 트리 비유해서 쉽게 기억하기

균형 이진 트리에서 탐색하는 건
"전화번호부를 한 장씩 넘기는 것"이 아니라, "중간을 찢어보면서 찾는 것"과 같아요.

• 📚 전화번호부를 펼쳐서 중간을 보고, 이름을 비교하고,
• 앞쪽이면 앞쪽 절반만 다시 보고,
• 또 중간을 보고, 앞 또는 뒤로 가고…

이걸 반복하는 거죠!

💽 하드 디스크, 파일, 그리고 포인터들의 세계

1) 디스크는 데이터를 어떻게 저장할까?

컴퓨터에서 하드 디스크는 단순한 저장 장치가 아닙니다.
그 안에는 수많은 포인터의 미로와, 파일 이름과 데이터 사이를 연결하는 복잡한 구조가 숨어 있어요.

🔹 디스크 저장 단위: 블록과 클러스터

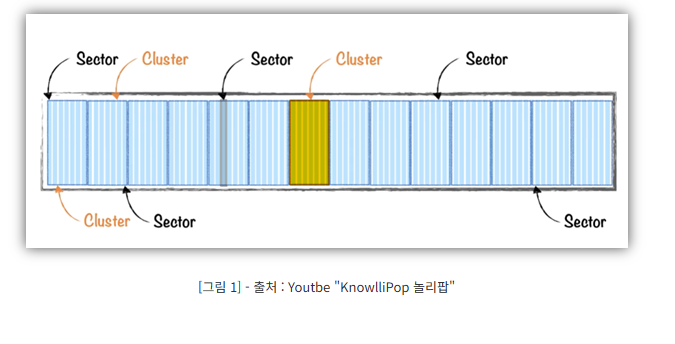
• 블록(Block): 디스크에서 데이터를 저장하는 가장 작은 단위 (예: 4KiB)
• 클러스터(Cluster): 여러 개의 연속된 블록 묶음

이상적으로는 하나의 파일이 한 클러스터에 저장되면 좋지만,
현실에서는 파일 크기가 클러스터보다 크거나 클러스터가 분산되어 있어요.
그래서 파일은 여러 위치에 나눠서 저장되고, OS는 이것을 연속된 것처럼 보여줍니다.

참고 : https://velog.io/@gwak2837/%EB%94%94%EC%8A%A4%ED%81%AC%EC%99%80-%EB%A0%88%EC%BD%94%EB%93%9C-%EA%B5%AC%EC%A1%B0

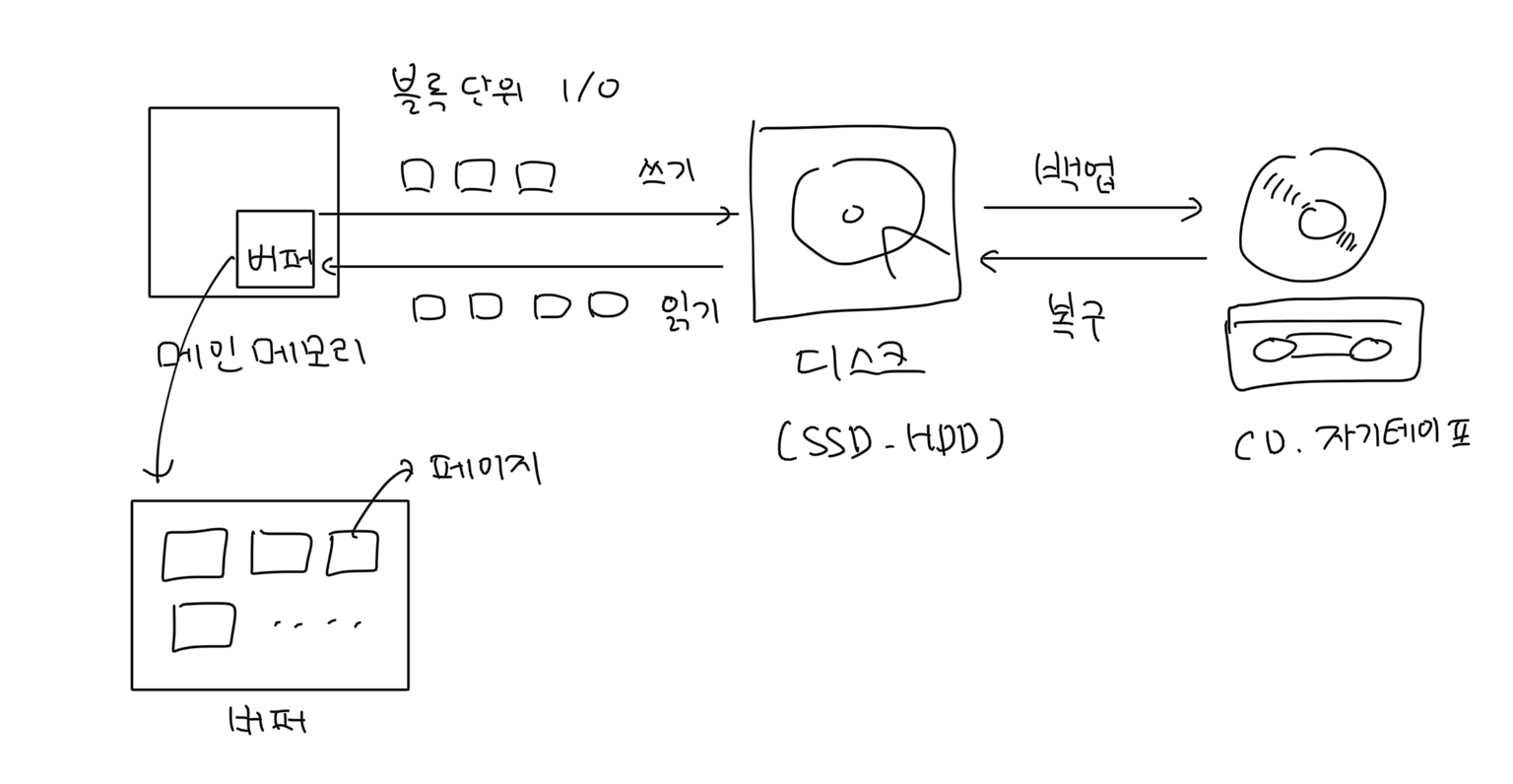
2) 문제: 데이터를 여러 블록에 나눠 저장하면 어떻게 추적하지?

단순히 포인터를 써서 연결하면 안 될까요?
→ 연결 리스트처럼 디스크 블록을 연결할 수도 있겠죠.

하지만 연결 리스트 방식의 단점은?

• 디스크 블록이 수십억 개면, 블록을 하나하나 순회해야 합니다.
• 속도는 최악의 경우 1초에 250블록 → 20억 개를 다 읽으려면 15년 걸림 😱

📌 메모리에서는 포인터 순회가 빠르지만, 디스크는 접근 비용이 비쌉니다.

3) 파일 이름 → 블록 연결: 아이노드(inode)

이 문제를 해결하기 위해 유닉스에서는 inode(아이노드)라는 개념을 사용합니다.

• inode = index + node
• 파일의 모든 정보를 담고 있는 구조체예요.

아이노드가 담고 있는 정보:

• 파일 이름, 소유자, 권한, 파일 크기 등
• 그리고! 데이터가 저장된 블록들의 "주소" (인덱스)

4) 블록 연결 방식: 직접 vs 간접 포인터

📌 [그림] 아이노드 구조

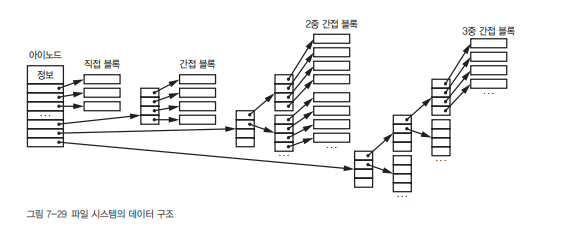
아이노드
 ├─ 직접 블록 포인터 (12개)
 ├─ 간접 블록 포인터 (1개)
 ├─ 이중 간접 포인터 (1개)
 └─ 삼중 간접 포인터 (1개)

✅ 직접 블록 (Direct Block)

• 아이노드가 직접 가리키는 블록 (12개)
• 예: 12 × 4KiB = 48KiB~49KiB까지 저장 가능
  → 대부분의 일반 텍스트 파일은 여기서 해결돼요.

✅ 간접 블록 (Indirect Block)

• 포인터가 또 다른 포인터 목록을 가리킴 (포인터를 가리키는 포인터)
• 1 블록에 4바이트 인덱스 1024개 → 4MiB 지원

✅ 이중/삼중 간접

• 포인터 → 포인터 목록 → 또 포인터 목록...
• 이중: 4GiB까지
• 삼중: 4PiB까지 저장 가능!

5) 디렉터리와 계층 구조

• 디렉터리는 파일 이름 → 아이노드 번호를 연결해주는 테이블입니다.
• 유닉스에서는 디렉터리조차도 하나의 파일로 다룹니다.
  → 그래서 디렉터리 안에 디렉터리, 즉 계층적 트리 구조가 가능해진 거예요!

6) 하드 링크 & 심볼릭 링크

• 여러 아이노드가 같은 데이터 블록을 참조할 수 있어요 → 하드 링크
• 파일이 아닌 파일 경로를 가리키는 링크도 가능해요 → 심볼릭 링크

📌 심볼릭 링크는 편리하지만, 문제는?

• 루프(loop)가 생길 수 있어요!
• 그래서 파일 시스템 탐색 시 무한 순회 방지 코드가 필요해요.

7) 사용 가능한 블록 추적: 비트맵 사용

디스크에 남은 공간(Free Space)을 추적하려면?

→ 가장 간단하면서 강력한 방법: 비트맵(bitmap)

• 각 블록마다 1비트씩 할당
  → 1: 사용 중, 0: 사용 가능

8TB 디스크 = 약 20억 블록 → 비트맵은 256MiB
디스크 크기에 비해 매우 적은 공간이므로 실용적!

• 비트맵은 RAM에 전체를 올릴 필요 없이, 일부만 캐싱해도 됨
• 64비트 연산으로 빠르게 빈 블록을 찾을 수 있음

8) 그런데, 시스템이 꺼지면?

디스크 작업 중 전원이 나가면?

• 비트맵 정보와 실제 블록 사용 상태가 불일치할 수 있음
• 이런 문제를 해결하기 위해 등장한 게 fsck (file system check)

⛑️ fsck

• 비트맵과 파일 시스템 트리를 비교해서 오류 수정

하지만? 디스크가 너무 커지면서 fsck 시간도 엄청 오래 걸리게 됐어요.

9) 최신 해결책: 저널링 파일 시스템 (Journaling FS)

• 디스크에 쓰기 작업을 하기 전, "일지(journal)"에 기록하고
• 작업이 완료되면 일지를 정리

→ 전원 오류가 나도, 작업 상태를 복구할 수 있어요!

대표적인 예:

• ext3/ext4 (Linux), NTFS (Windows), APFS (macOS)

좋아요! 말씀해주신 섹터(Sector)와 슬랙(Slack) 개념까지 포함해서 정리해드릴게요.
스토리텔링 형식을 유지하면서, 섹터/슬랙이 파일 저장과 어떤 관계가 있는지, 왜 발생하는지, 어떤 영향을 주는지 함께 풀어볼게요.

10) 하드 디스크 구조를 더 깊이 들여다보자

지금까지 블록, 클러스터, 아이노드 등 디스크의 논리 구조를 살펴봤다면,
이제는 그 기반이 되는 물리 구조와, 그에 따른 저장 비효율 문제(slack)까지 함께 정리해볼게요!

🔹 디스크 저장의 가장 작은 단위: 섹터(Sector)

• 섹터는 디스크에서 데이터를 읽고 쓰는 가장 작은 물리 단위예요.
• 하나의 섹터 크기: 보통 512바이트 또는 4KiB

✅ 디스크는 실제로 “파일”을 저장하지 않아요.
데이터를 “섹터 단위로 나눠서 저장”할 뿐입니다.

🔸 논리 단위와의 연결: 블록과 클러스터

• 운영체제는 물리 섹터를 모아서 블록(block) 단위로 사용합니다.
• 블록 여러 개가 묶이면 클러스터(cluster)가 됩니다.

[디스크 물리적 구조]  
 └─ 섹터(512B) × N → 블록(4KiB)  
 └─ 블록 × N → 클러스터

📌 실제 디스크는 섹터 단위로 동작하고, OS는 이를 블록 단위로 포장해서 사용합니다.

🔹 그런데 여기서 문제가 생긴다: 슬랙 공간(Slack Space)

❓ 슬랙이란?

• 어떤 파일이 블록보다 작을 때,
  남은 블록 공간이 비어 있어도 디스크는 전체 블록을 점유합니다.

📦 예시

• 블록 크기: 4KiB (4096B)
• 저장하려는 파일: 1,000B
  → 남은 3,096B는 사용할 수 없음 = 슬랙(Slack)

┌───────────────┐
│ 1,000B 데이터 │
│ 슬랙 공간 3KB │  ← 이건 낭비됨
└───────────────┘

✅ 슬랙 공간은 보안 이슈로도 중요해요.
이 빈 공간에 지워지지 않은 이전 데이터가 남아 있을 수도 있거든요.

🔹 디스크에 데이터를 저장할 때 흐름은 이렇게 흘러갑니다

1. 파일을 저장하면
2. OS가 파일 이름을 디렉터리에 등록하고
3. 아이노드에 파일 정보를 기록하고
4. 아이노드가 데이터 블록을 가리킴
5. 데이터 블록은 디스크의 섹터에 매핑되고
6. 작은 파일이면 슬랙이 발생

📌 요약 그림

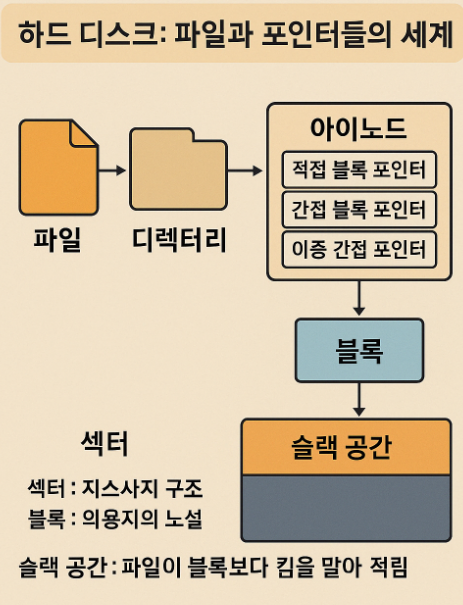
파일 → 디렉터리 → 아이노드  
아이노드 → [직접 / 간접 블록 포인터] → 블록 → 섹터  
(→ 남는 섹터 공간 = 슬랙)

🔍 디스크 저장 구조 정리 표

구분	설명
섹터 (Sector)	디스크의 물리적 저장 단위 (512B 또는 4KiB)
블록 (Block)	OS가 섹터를 모아서 만든 논리 저장 단위 (보통 4KiB)
클러스터 (Cluster)	블록 여러 개를 묶은 단위
슬랙 공간 (Slack Space)	파일이 블록보다 작을 때 남는 공간. 낭비되는 여유 공간
아이노드 (inode)	파일 정보 + 해당 파일의 데이터가 저장된 블록 인덱스를 담은 구조체
직접/간접 포인터	아이노드에서 데이터 블록을 가리키는 포인터 구조
디렉터리	파일 이름 → 아이노드 연결 테이블
비트맵	블록 사용 여부 추적 구조 (1: 사용 중 / 0: 가용)

컴퓨터가 작은 텍스트 파일 하나를 저장할 때도,
실제로는
디렉터리 → 아이노드 → 블록 → 섹터 → 슬랙까지 고려된 저장 공간을 다 동원합니다.

단순해 보이는 저장이 실제로는
운영체제와 하드웨어가 공동으로 처리하는 복잡한 작업인 셈이죠!

💬 하드 디스크 안에는 마치 작은 운영체제 같은 정교한 데이터 구조가 숨어 있어요.
파일을 하나 저장한다는 건 사실, 수많은 포인터와 맵, 링크, 트리, 저널링 로직이 동작하는 일입니다!

참고 : HDD 구조

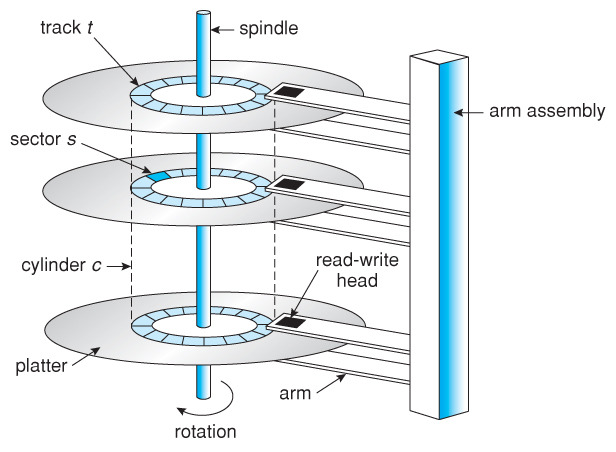
• Platter = track + ... + track = Track 50K ~ 100K개 = 12.5 ~ 100GB
• Track = sector + ... + sector = Sector 500 ~ 2000개 = 256KB ~ 1MB
• Sector = 512 bytes
• Head: 데이터를 자기적으로 읽거나 쓰는 장치

HDD 처리 시간

• Seek time: Head를 특정 track에 위치시키는 시간
• Rotational latency: 특정 sector를 찾기 위해 디스크 원판을 돌리는 시간
• Data transfer time: Head를 통해 자기적으로 저장된 데이터를 읽는 시간
• Seek time과 rotational latency는 디스크 헤드의 기계적인 움직임이 필요하기 때문에 상대적으로 시간이 오래 걸리지만, data transfer time은 전기적인 동작이기 때문에 상대적으로 짧습니다.

그리고 만약 동일한 track 위에 데이터를 모아서 저장한다면 해당 데이터에 접근할 때 seek time이 줄어들 수 있어 데이터 전송 속도가 빨라질 수 있습니다.

레코드 구조

🧾 레코드(Record)란?
레코드란, 하나의 관련된 필드(field)들을 묶어 놓은 데이터의 단위입니다.
우리가 흔히 엑셀, 테이블, DB에서 보는 "한 줄(row)"이 바로 레코드에 해당해요.

• 데이터베이스 = 파일 + ... + 파일
• 파일 = 테이블 + ... + 테이블
• 테이블 = 레코드 + ... + 레코드
• 레코드 = 필드 + ... + 필드
• 레코드 << 블록

일반적으로 한 파일엔 여러 종류의 테이블이 들어갈 수 있고, 동일한 테이블의 레코드일지라도 개별 레코드 크기는 다를 수 있습니다. 그리고 레코드 크기는 블록 크기에 비해 충분히 작다고 가정합니다.

고정 길이

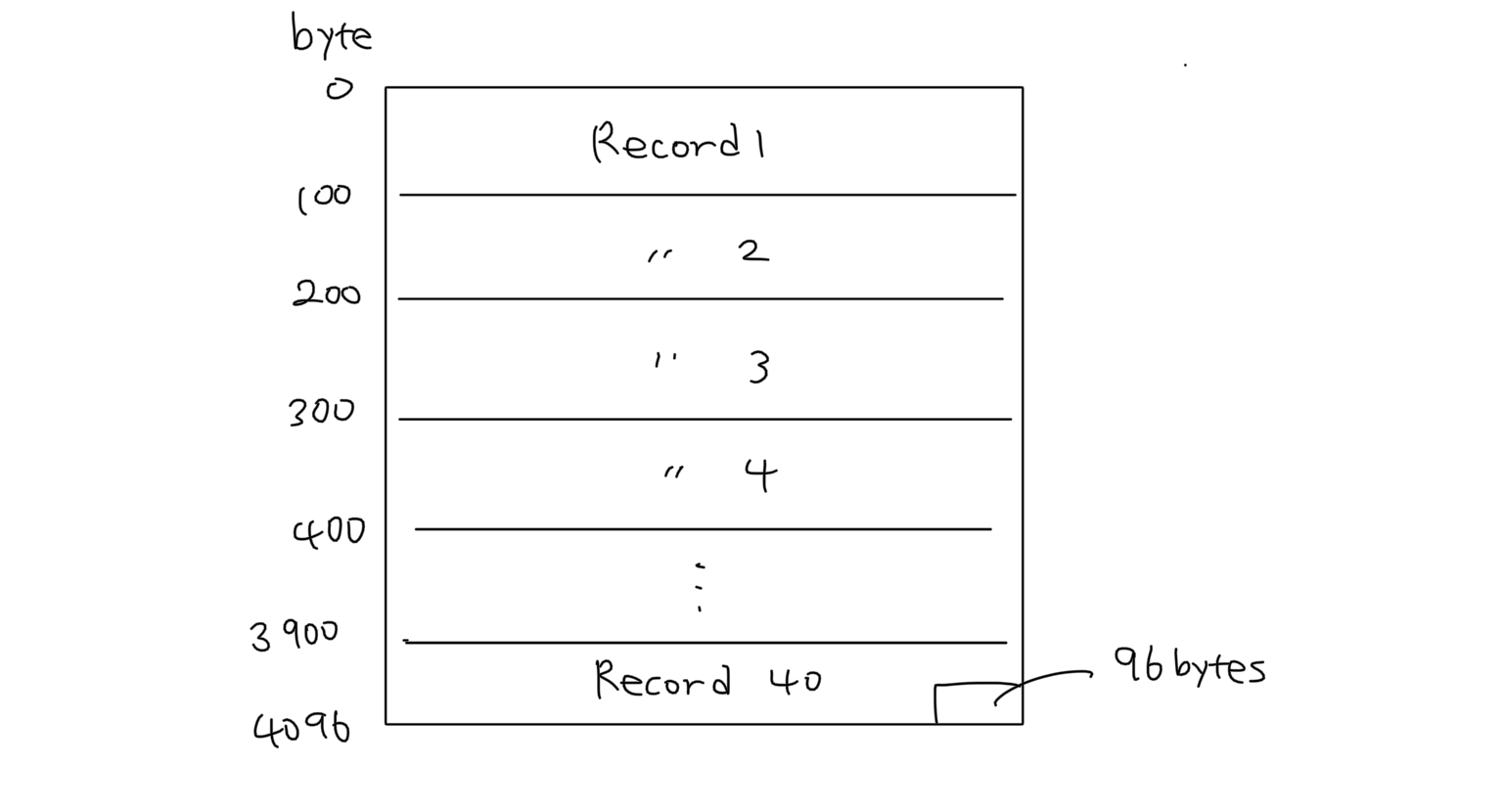
특정 테이블의 레코드 크기는 모두 동일하다고 가정한 경우입니다. 위 그림과 같이 한 블록의 크기가 4KB라고 가정했을 때 레코드 크기가 100 bytes인 경우 한 블록에 최대 40개의 레코드를 저장할 수 있습니다.

나머지 96 bytes는 비어있는 공간으로서 굳이 하나의 레코드를 쪼개서 블록을 꽉 채우지 않고 여유공간을 조금 남겨 놓는 것이 나중에 CRUD 작업을 수행할 때 좋다고 합니다.

가변 길이

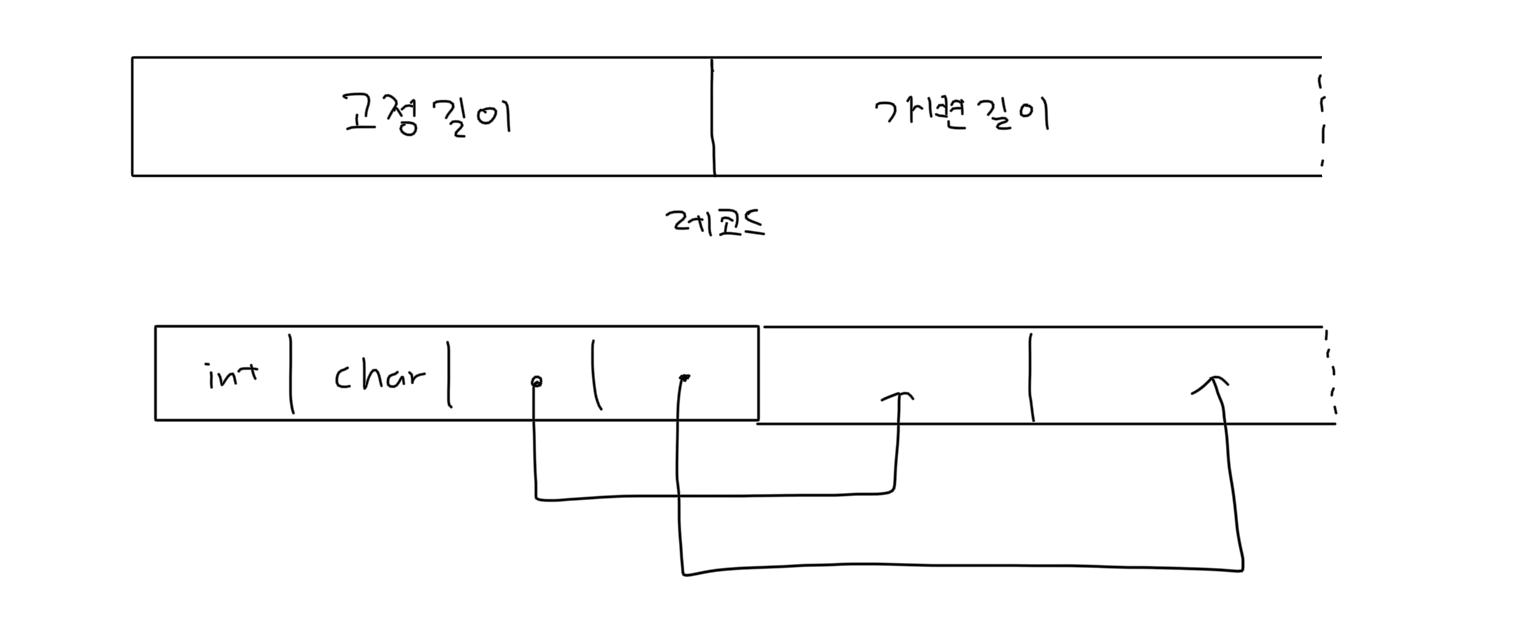
레코드 안에는 여러 필드가 존재하는데 문자열 자료형의 경우 동일한 테이블의 레코드일지라도 각 필드 길이가 달라질 수 있습니다. 그래서 일반적으론 가변 길이 레코드가 많이 사용됩니다.

가변 길이 레코드는 위 그림과 같이 왼쪽에 고정 길이 필드를 모아 놓고, varchar와 같은 가변 길이 필드는 포인터와 데이터 길이로 관리하여 실제 문자열 데이터는 레코드 오른쪽 부분에 저장합니다.

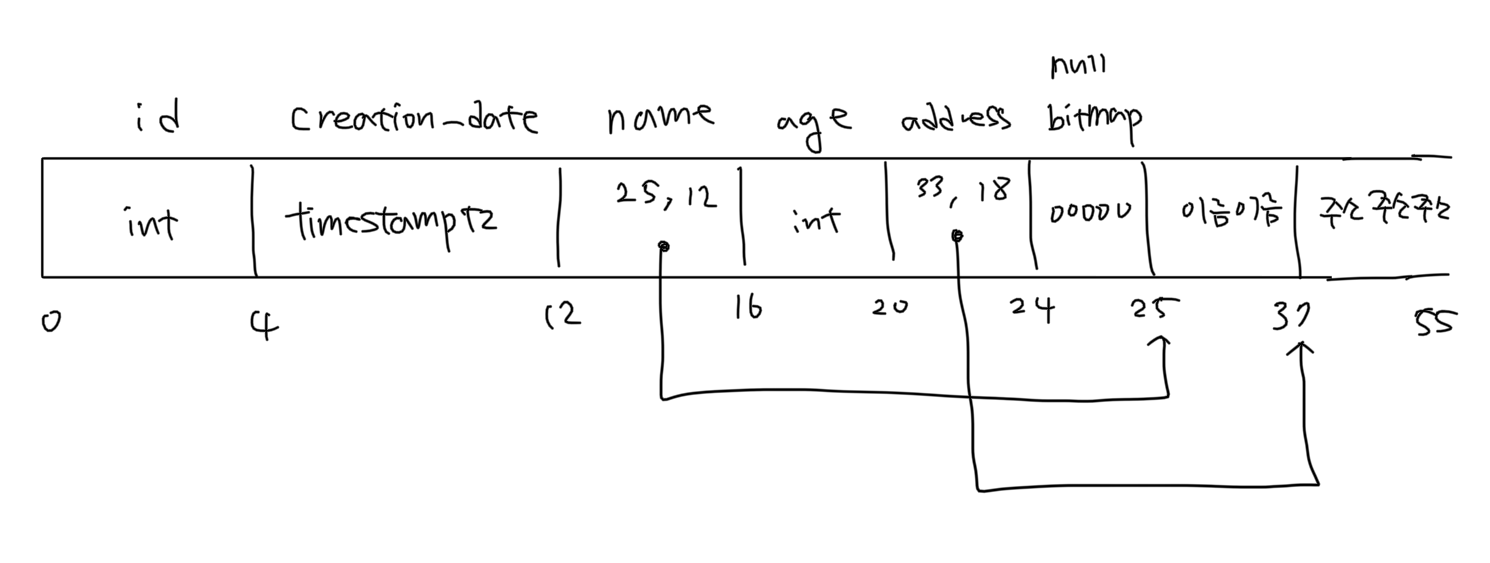
예를 들어 위와 같은 구조를 가진 test 테이블에 레코드를 삽입했을 때 해당 레코드의 물리적인 모습은 위 그림과 같습니다. (포인터는 4 bytes로 관리되고 한글은 UTF-8로 처리된다고 가정합니다.)

출처 : 더 자세히 읽어보기 : 데이터베이스와 디스크 구조

정리

지금까지 이야기한 디스크, 블록, 섹터의 흐름에서 레코드(record)는 그보다 한 단계 논리적인 데이터 단위입니다.
한마디로 말하면, "파일 안에 저장된 실제 의미 있는 데이터 단위"라고 할 수 있어요.

학번	이름	학과	학년
1001	홍길동	컴퓨터공학	3

➡️ 이 한 줄이 바로 1개의 레코드입니다.
그리고 각각의 칸(학번, 이름 등)은 필드(field)라고 해요.

💽 레코드 vs 블록 vs 섹터

용어	의미	단위	관계
레코드	의미 있는 논리 데이터 단위 (예: 학생 1명 정보)	수십~수백 바이트	파일 안에 여러 개 존재
블록	OS가 데이터를 관리하는 논리 저장 단위	보통 4KiB	여러 레코드가 들어감
섹터	디스크가 실제로 읽고 쓰는 물리 단위	512B ~ 4KiB	블록이 섹터에 저장됨

🔄 예를 들어 정리하면:

1. 당신이 "학생 목록"이라는 파일을 만든다면,
2. 그 안에는 레코드들이 여러 개 저장됨
3. 이 레코드들은 하나 또는 여러 개의 블록에 저장되고
4. 블록은 결국 디스크의 섹터에 기록됨

레코드는 논리적인 데이터 단위,
블록은 OS의 저장 단위,
섹터는 하드웨어의 물리 저장 단위입니다.

📌 요약

구분	정의	비유
레코드	실제 저장하고자 하는 데이터 한 단위	엑셀의 한 줄
블록	OS가 다루는 저장 단위	책의 한 페이지
섹터	하드디스크의 물리적 단위	종이의 한 조각

훌륭한 내용을 주셨네요! 이 내용을 기반으로 발표나 블로그용으로 딱 맞게
스토리텔링 형식 + 시각적 흐름 + 핵심 개념 비교 중심으로 다시 정리해드릴게요 😊

---

📚 메모리에는 2진 트리, 디스크에는 B트리 — 디스크 친화적인 데이터 구조 이야기

1) 2진 트리는 메모리에서는 좋지만…

우리는 지금까지 데이터를 정렬하고 빠르게 탐색하려고 이진 탐색 트리(Binary Tree),
특히 균형 이진 트리(Balanced Binary Tree)를 써왔어요.

• ✔ 검색 속도: O(log N)
• ✔ 메모리 안에서는 연산이 빠르고 구조가 단순
• ❌ 그런데… 파일이 수 GB, 수 TB로 커져서 디스크에 저장해야 할 때는?

🧱 문제: 2진 트리는 디스크에 부적합해요

• 노드 하나가 너무 작아서 디스크 블록을 꽉 채우지 못하고 낭비
• 디스크는 데이터를 블록 단위(보통 4KiB)로 읽기 때문에,
  트리 노드가 작을수록 많은 블록을 낭비하게 됨
• 검색하려면 노드를 계속 따라가야 하고,
  그럴 때마다 디스크 I/O가 발생해서 매우 느림

👉 이럴 땐? 2진 트리가 아니라 디스크에 최적화된 트리 구조가 필요합니다.

2) 등장! 디스크를 위한 데이터 구조: B-트리

1971년, 보잉 사의 연구소에서
루돌프 바이어(Rudolf Bayer)와 에드 맥크레이트(Ed McCreight)는
디스크 저장에 유리한 자료구조로 B-트리(B-tree)를 제안했어요.

🔍 B트리는 뭐가 다를까?

특징	2진 트리	B-트리
자식 수	최대 2개	수십 개 이상 가능 (M차 B-트리)
노드 크기	작음 (보통 1키)	큼 (디스크 블록 하나를 채우는 크기)
저장 위치	보통 메모리	디스크 블록 단위
탐색 방식	한 번에 1단계	한 번에 수십 개 키 비교 가능
I/O 효율	낮음 (많은 블록 접근)	높음 (적은 블록으로 더 많은 정보)

📦 예시로 이해하는 B-트리

🎯 1. 2진 트리의 예

           Ken
         /     \
     Dennis   Mike
    /     \      \
 Brian   Doug    Steve

→ 각 노드는 단 1~2개의 자식만 가지며,
→ 노드를 따라가려면 여러 번 디스크 블록을 읽어야 해요 😥

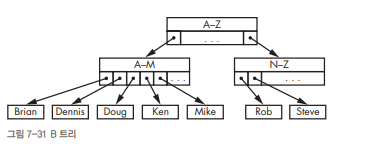
🎯 2. B-트리 구조의 예

             [ A–Z ]
             /     \
       [ A–M ]    [ N–Z ]
       / | | \       ...
Brian Doug Ken Mike Rob Steve

• 각 노드에 여러 개의 키와 자식 포인터를 저장
• 한 노드가 디스크 블록 하나에 딱 맞게 설계됨
• 한 블록만 읽어도 여러 검색 결과를 포함

📌 "한 번의 디스크 접근으로 더 많은 정보를 확인" → I/O 횟수 ↓ 검색 속도 ↑

✅ B-트리의 설계 핵심

1. 노드 하나 = 디스크 블록 하나

   • 디스크는 어차피 블록 단위로 데이터를 읽으니,
     노드를 작게 나눌 필요가 없음

2. 많은 자식 가지기

   • 예: 하나의 노드에 100개의 키가 들어 있으면,
     트리의 높이를 log₁₀₀(N)으로 줄일 수 있음
     → 굉장히 얕은 트리! (즉, 빠른 탐색)

3. 균형 유지도 쉬움

   • 자식이 너무 많아지면 분할(split),
     너무 적으면 병합(merge)

즉, 균형 잡힌 다진 트리 + 디스크 친화적 블록 설계가 B-트리의 핵심이에요!

🤔 여유 공간은 낭비 아닐까?

맞아요. B-트리는 자식 포인터를 저장할 공간이 많기 때문에,
사용되지 않는 포인터 칸(= 공간 낭비)가 생기기도 해요.

하지만 이 낭비는 합리적인 트레이드오프입니다:

• 디스크 접근 횟수를 줄일 수 있다면,
• 약간의 공간 낭비는 충분히 감수할 수 있어요!

🌲 2진 트리는 메모리에서 빠르고 간단한 자료구조입니다.
📀 하지만 데이터를 디스크에 저장하는 순간, 우리는 블록 단위 처리, 디스크 I/O, 포인터 수 같은 하드웨어 특성까지 고려해야 하죠.

그래서 데이터베이스, 파일 시스템 등 디스크 기반 시스템의 핵심 자료구조는
바로 이 B-트리 또는 그 변형(B+트리, B*트리 등)입니다.

추가 정리 🧱 블록 구조와 레코드의 세계: "데이터는 어떻게 공간을 차지할까?"

1. 디스크 블록은 데이터의 방

데이터베이스는 데이터를 파일처럼 저장하지 않아요.
모든 데이터는 일정 크기의 디스크 블록 단위(보통 4KB~16KB)로 나뉘어 저장됩니다.
이 블록은 마치 방 하나, 그리고 그 안에 레코드들이 자리를 잡고 있어요.

2. 고정 길이 vs 가변 길이 레코드

🧱 고정 길이 레코드

• 레코드마다 크기가 동일함
• 빠르게 읽고, 빠르게 저장하지만
• ❌ 빈 공간이 낭비됨
• ❌ NULL 필드나 varchar 관리가 불리함

🧩 가변 길이 레코드

• 크기가 각각 다름
• 🎯 공간을 더 효율적으로 사용
• ⛓️ 대신 간접적인 접근 방식이 필요함

3. 레코드 삭제의 3가지 방식

방법	설명	장점	단점
방법 1	뒤 레코드를 한 칸씩 앞으로 이동	레코드 정렬 유지	많은 연산 필요
방법 2	마지막 레코드를 앞으로 옮김	빠름	순서가 깨짐
방법 3	삭제된 레코드를 연결 리스트로 관리	빠르고 간단	헤더 공간 차지

이 세 가지 방법은 모두 속도 ↔ 정렬 유지 사이의 균형을 고민한 결과예요.

4. 가변 길이 레코드 블록 구조

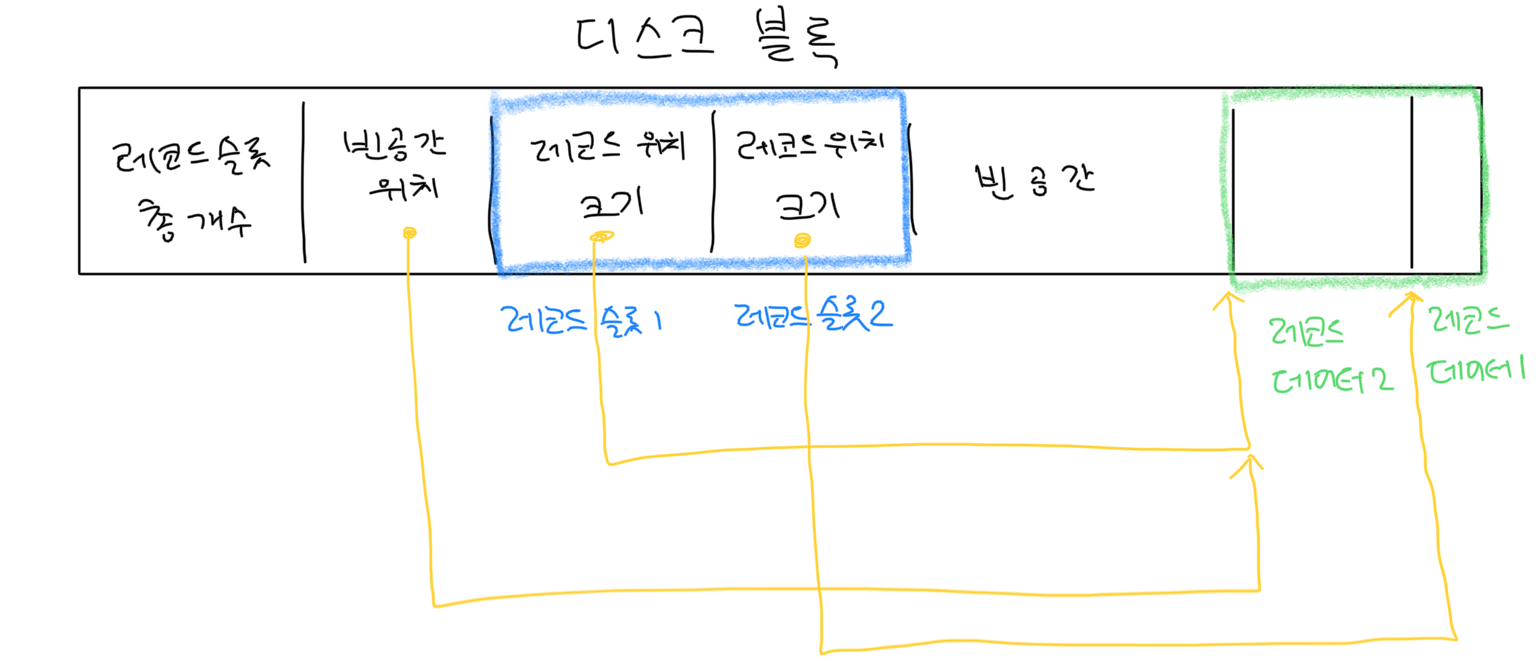
블록은 두 부분으로 나뉩니다:

[ 레코드 슬롯 ]   ←← 왼쪽에서 오른쪽으로 쌓임
[ 자유 공간 (Free Space) ]
[ 레코드 데이터 ] ←← 오른쪽에서 왼쪽으로 쌓임

구성 요소	설명
레코드 슬롯	각 레코드의 위치와 길이 정보를 담고 있음
레코드 데이터	실제 데이터가 저장되는 공간
Free Space	슬롯과 데이터 사이의 남는 공간

5. 간접 접근(indirect access)의 이유

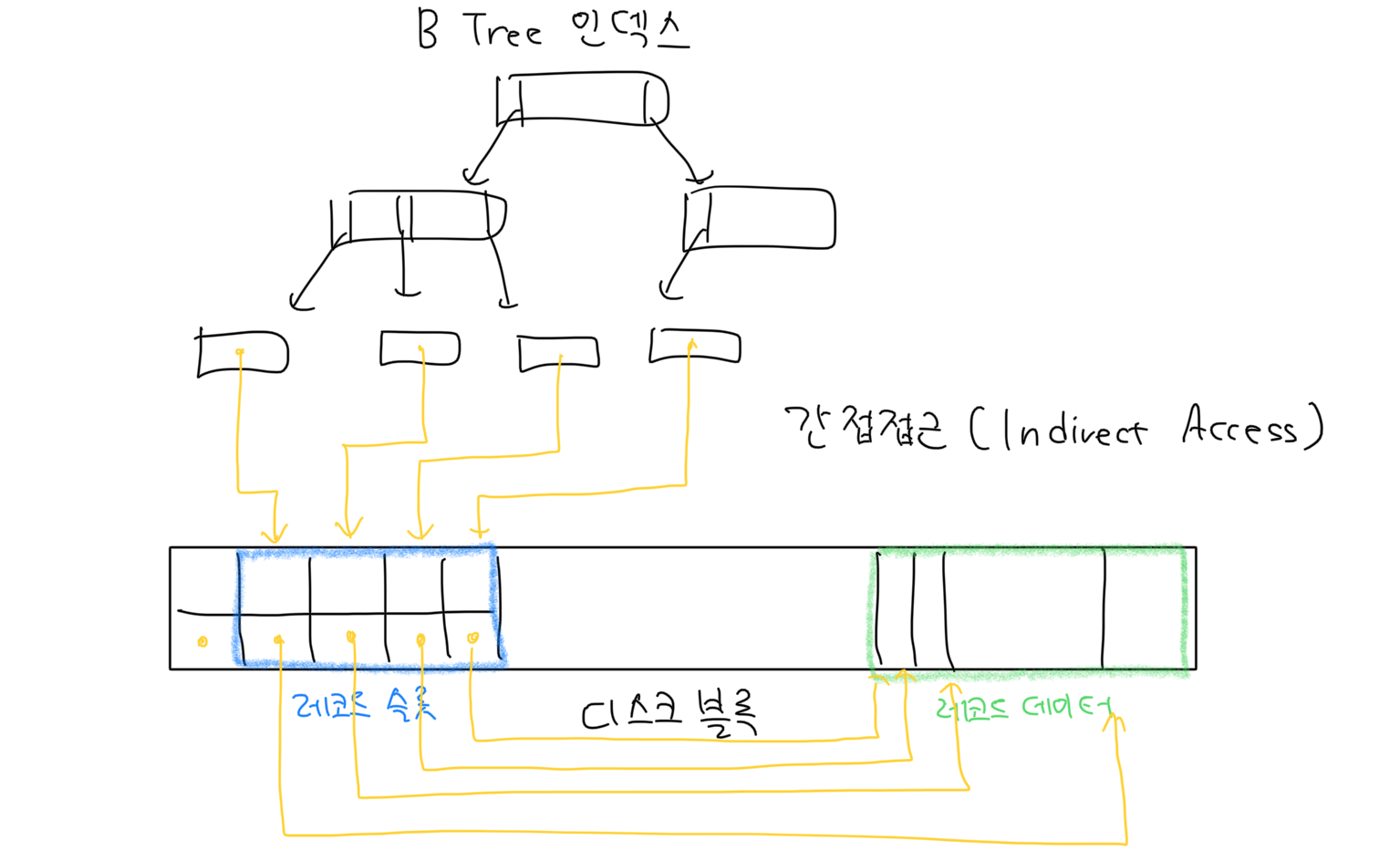
• 레코드는 삽입/삭제/수정에 따라 물리적 위치가 자주 바뀜
• 직접 주소로 접근하면 → 인덱스, 외부 포인터 전부 수정해야 함
• 해결책: 슬롯에만 접근하도록 함 → 레코드 위치가 바뀌어도 외부 수정 불필요

🎯 슬롯 → 레코드 위치 → 데이터
이 구조가 DB의 유연성과 안정성을 보장해줍니다!

6. 레코드 삽입 / 수정 / 삭제 과정

작업	흐름
삽입	레코드는 free space의 오른쪽에, 슬롯은 왼쪽에 생성
수정	데이터가 커지면 옆으로 밀고, 슬롯 정보 업데이트
삭제	레코드는 옮기고, 슬롯엔 삭제 표시만 함. 재활용 가능

7. 대용량 데이터는 어떻게 저장할까?

방식	설명	장단점
방식 1	OS 파일 시스템에 저장 (DB는 경로만 기억)	간단하지만 파일 삭제 시 오류 발생 가능
방식 2	파일은 OS에 저장, DB가 읽기/쓰기 관리	안정적, 하지만 I/O 복잡성 있음
방식 3	데이터를 조각내어 여러 블록에 저장 + B+Tree 인덱싱	범위 탐색, 삽입/삭제에 유리. 고급 방식

대표적인 데이터 유형

• BLOB: 이미지, 영상 등
• CLOB: 문서, 텍스트 등

📚 인덱스(Index)는 왜 필요할까? — 데이터 속에서 빠르게 찾기 위한 비밀 무기

읽으면 좋은 글이자 출처 글 : MySQL 인덱스 구조와 원리의 이해

1) 문제의 시작: 데이터는 많고, 시간은 없다

데이터베이스의 목적은 단순히 데이터를 "저장"하는 게 아니라
원하는 데이터를 빠르게 찾는 것에 있어요.

하지만…

• 테이블에 데이터가 수십만, 수백만 건이 쌓이면?
• 조건에 맞는 데이터를 찾기 위해 모든 행을 검사해야 한다면?

🐢 검색 성능은 느려지고,
😡 사용자 체감 속도는 낮아지고,
🔥 서비스 품질이 무너집니다.

2) 색인(Index)의 원리: 책의 "색인 페이지"처럼!

인덱스는 우리가 책에서 흔히 보는 색인(index page)과 똑같아요.

• 원하는 단어가 어느 페이지에 있는지 미리 정리
• 정렬된 상태로 빠르게 탐색 가능
• 자주 찾는 용어만 담고, 위치만 요약해 기록

📌 인덱스는 검색을 빠르게 하기 위해 존재합니다.
→ 대신 삽입/수정/삭제 속도는 희생해야 해요.

3) 인덱스의 구조: B-Tree가 기본!

B-Tree 인덱스

출처 : http://www.gurubee.net/wiki/pages/12517389

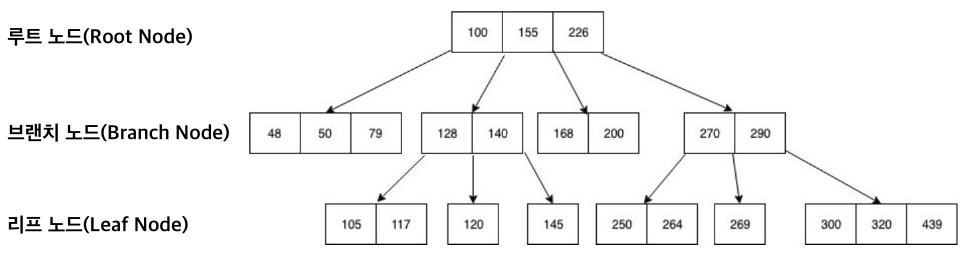
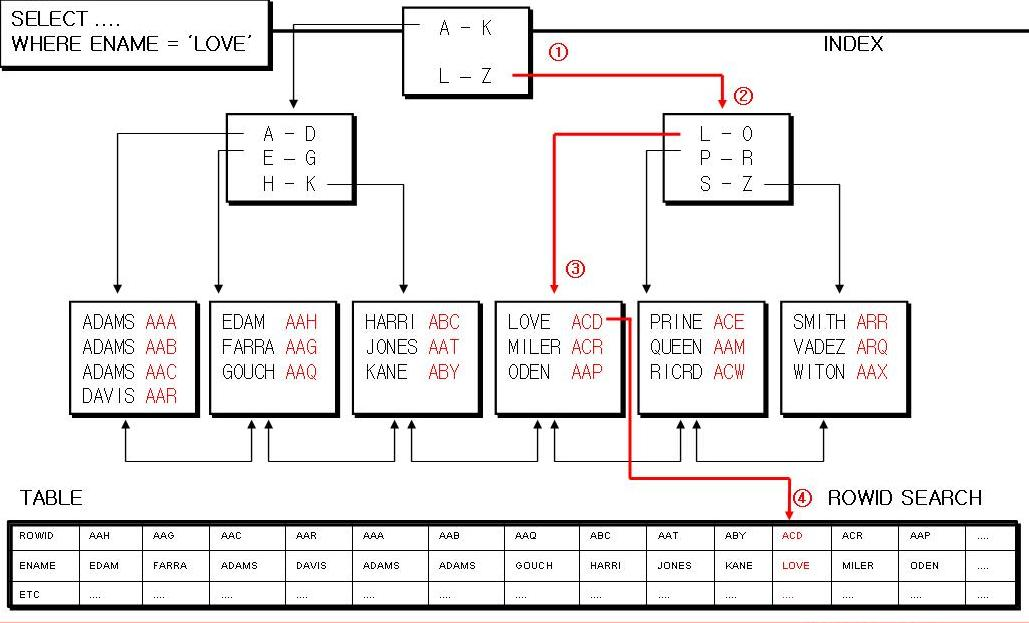
• 대부분의 RDBMS는 B-Tree 또는 변형(B+Tree)을 사용
• 루트 → 브랜치 → 리프 구조로 구성
• 리프 노드에 실제 데이터 주소(또는 프라이머리 키)가 있음

InnoDB의 클러스터형 인덱스 구조

• 프라이머리 키 값 순서대로 데이터 파일 자체를 정렬 저장
• 세컨더리 인덱스를 통해 찾으면
  → 리프 노드에 있는 프라이머리 키로 한 번 더 탐색 필요

4) 레코드 찾기 흐름 예시

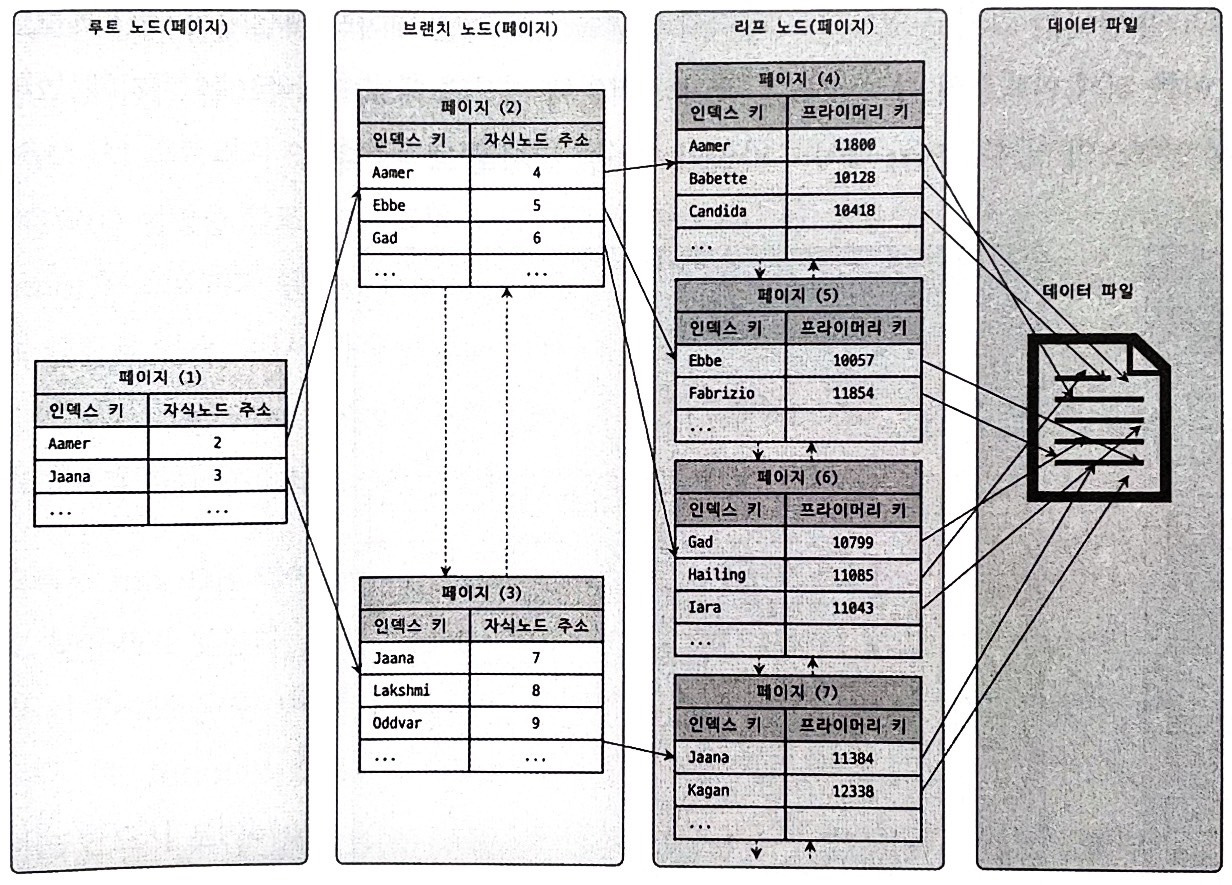
예: "Gad"라는 이름을 검색한다고 가정

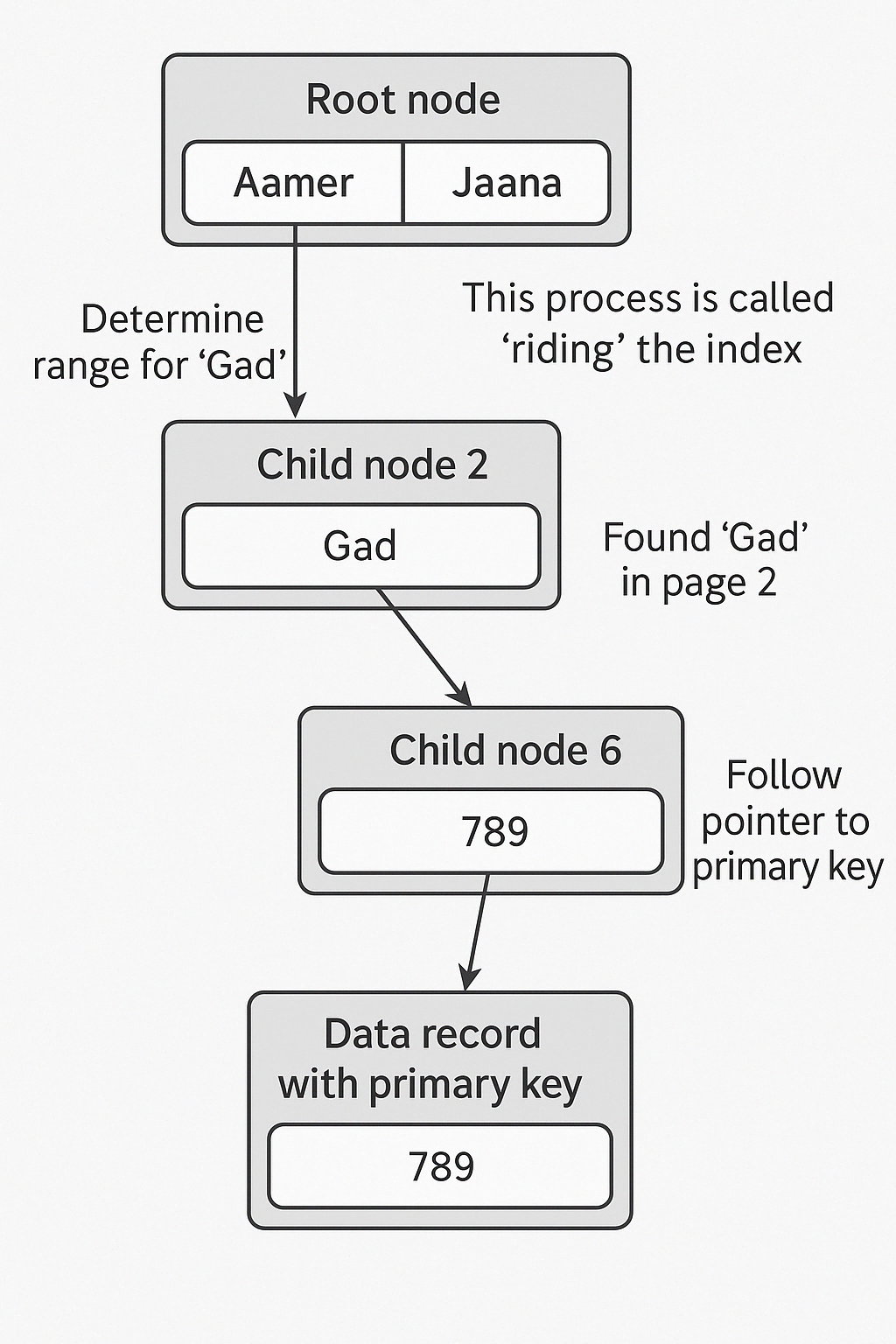
1. 루트 노드에서 "Gad"가 들어갈 범위를 판단
2. 자식 노드 페이지 2번으로 이동
3. 2번 페이지에서 "Gad"를 발견
4. 해당 리프 노드가 가리키는 프라이머리 키 주소를 통해
   실제 레코드에 접근

✅ 이 과정이 인덱스를 "탔다"고 부르는 것입니다

루트 노드
  └─ "Aamer" vs "Jaana" 사이? → 자식 노드 2번
    └─ "Gad" 있음 → 자식 노드 6번
      └─ 프라이머리 키 주소 → 실제 레코드 찾기!

5) 인덱스의 트레이드오프

장점	단점
빠른 조회(SELECT)	느려지는 INSERT/UPDATE/DELETE
정렬된 데이터 기반 빠른 범위 탐색	정렬 유지 위한 오버헤드
고성능 검색 최적화	공간 사용 증가, 관리 복잡

SELECT가 중심인 대부분의 서비스에서
인덱스의 이점은 단점을 능가합니다.

6) 인덱스 사용을 결정짓는 요소들

요소	설명
인덱스 키 크기	너무 크면 노드 당 키 수 줄어 → 성능 하락
트리 깊이	깊을수록 접근 단계 많아짐
선택도	유니크할수록, 골고루 퍼질수록 좋음
읽는 레코드 수	전체의 20% 이하일 때 효율적
유니크 속성	고유한 값이면 "즉시 종료" 가능

7) 인덱스 검색 방식

방식	설명
인덱스 레인지 스캔	일부 범위만 탐색 (이상적)
인덱스 풀 스캔	인덱스를 전체 순회 (비효율)
루스 인덱스 스캔	듬성듬성 읽는 최적화
인덱스 스킵 스캔	선두 컬럼 없이도 부분 인덱스 탐색 (특수 조건만 가능)

8) 멀티 컬럼 인덱스의 핵심: 정렬 순서

(dept_no, emp_no)
(emp_no, dept_no)

• 쿼리 조건이 WHERE dept_no = 'd001' AND emp_no >= 1000이면?
  1번 인덱스가 훨씬 효율적!

✅ 멀티 컬럼 인덱스는 항상 앞에 오는 컬럼 순서대로 정렬됨
→ 쿼리에 맞는 순서를 선택하는 것이 매우 중요해요

9) 인덱스를 사용할 수 없는 경우

비효율/불가 조건	이유
NOT, NOT IN, NOT BETWEEN	정렬로 범위를 좁히기 어려움
"%PRO" 형태 LIKE	앞부분이 정렬되지 않음
SUBSTRING(column, 1, 1) = 'X'	연산 후 값은 인덱스 순서 무효
함수나 형 변환 포함	정렬 기반 탐색이 불가
콜레이션 다름	인덱스 키 비교 불가능

💬 마무리

인덱스는 빠른 조회의 시작점이자,
올바른 설계가 아니면 오히려 성능의 덫이 됩니다.

인덱스를 잘 이해하고, 테이블 구조와 쿼리를 함께 고려해서
읽을 때 빠르고, 쓸 때 효율적인 설계를 해보세요 😊

🧠 기억은 벽에 붙은 포스트잇처럼 – 해싱의 세계

1) 왜 해싱이 필요할까?

우리는 지금까지 데이터를 검색할 때 리스트나 트리 같은 구조를 순차적으로 탐색해야 했어요. 즉, “얘가 맞니?” “아니야?” 하고 여러 번 비교하며 찾아야 했죠.

하지만 데이터를 많이 저장하거나 검색해야 하는 상황이라면, 이런 방식은 너무 느려요. 그래서 훨씬 빠르게 원하는 정보를 찾을 수 있는 방법이 필요했어요.

그게 바로 오늘의 주인공, 해싱(Hashing)입니다.

2) 해싱이란 무엇인가요?

해싱은 한마디로 말해,

"키(찾고자 하는 기준)를 통해 계산된 위치에 바로 가서 데이터를 꺼내오는 방식"이에요.

예를 들어, 우리가 어떤 정보를 찾으려고 할 때, 그걸 직접 주소를 계산해서 찾아가는 것처럼 동작해요. 마치 친구 집에 갈 때, 주소만 알면 내비게이션으로 바로 가는 것처럼요.

3) 해시 함수의 역할

해싱의 핵심은 바로 해시 함수(hash function)입니다.

해시 함수는 다음과 같은 일을 합니다:

• 입력 값(예: 문자열 'Hell')을 숫자로 변환해서
• 해시 테이블이라는 배열의 인덱스로 바꿔주는 역할을 해요.

예시: 문자열 'Hell' → ASCII 코드로 바꿔서 다 더한 값 → mod 11 → 인덱스 4번에 저장!

이때, 해시 테이블의 각 칸을 버킷(bucket)이라고 부릅니다.

4) 해시 함수는 어떤 것이 좋을까?

좋은 해시 함수는 이렇게 생겼습니다:

1. 계산이 빠르다
2. 골고루 버킷에 데이터를 분산시킨다
3. 해시 테이블 크기를 소수(prime number)로 정하면 충돌이 적다

간단한 해시 함수 예시:

모든 문자의 ASCII 코드 값을 더한 뒤, 해시 테이블 크기(예: 11)로 나눈 나머지를 인덱스로 사용

5) 해시 충돌과 해결법

하지만 세상은 그렇게 단순하지 않죠. 같은 해시값이 나오는 충돌(collision)이 발생할 수 있어요.

예시:

• 'Scarlet'과 'Alligator'는 같은 해시값을 가질 수 있어요! → 둘 다 3번 버킷으로 가야 해요.

이때 사용하는 방법이 바로 해시 체인(hash chain)입니다.

해시 체인의 방식

각 버킷에 연결 리스트(Linked List)를 달아서 충돌된 데이터를 함께 저장

예시 그림:

버킷 3:
[Scarlet] → [Alligator]

이렇게 하면 충돌이 나도 데이터를 모두 저장할 수 있어요.

삽입 방식의 차이

• 빠른 삽입이 필요하다면: 새 데이터를 체인의 앞쪽에 넣어요
• 검색을 빠르게 하고 싶다면: 삽입 정렬 방식으로 넣어요

6) 해시 테이블 확장

• 저장할 데이터 수를 미리 알 수 없을 경우 → 해시 테이블이 꽉 차요
• 이럴 땐 크기를 늘려야 해요 → 단, 확장은 비싼 연산이에요 (많은 데이터 복사 필요)

하지만 자주 일어나지 않으므로, 충돌보다 훨씬 낫다고 볼 수 있어요.

7) 완전 해시 (Perfect Hash)

꿈의 해시 함수!
모든 키가 절대 충돌하지 않도록 각각 다른 인덱스에 정확히 저장된다면?

이걸 완전 해시(perfect hash)라고 부릅니다.

하지만 현실은…

“모든 키를 미리 알아야만 완전 해시 함수를 만들 수 있어요.”

즉, 실제 시스템에선 거의 불가능한 이상형입니다.

📌 해시 테이블 요약 정리

개념	설명
해시 함수	키를 인덱스로 바꾸는 함수
해시 테이블	인덱스를 기반으로 데이터 저장
버킷	해시 테이블의 각 칸
충돌	서로 다른 키가 같은 인덱스를 가질 때
해시 체인	충돌된 데이터를 연결 리스트로 저장
완전 해시	충돌이 아예 없는 이상적 함수

📍 그림으로 이해하기

🧩 해시 체인을 의인화한 그림

• 왼쪽에서부터 해시 함수가 각 캐릭터(키)를 바구니에 던지는 장면!
• 같은 바구니에 들어가서 줄을 서는 캐릭터들 = 해시 체인!

출처

• https://eine.tistory.com/entry/%EC%BA%90%EC%8B%9C-%EB%A9%94%EB%AA%A8%EB%A6%AC%EC%99%80-%EB%A9%94%EB%AA%A8%EB%A6%AC-%EA%B3%84%EC%B8%B5%EA%B5%AC%EC%A1%B0-%EA%B7%B8%EB%A6%AC%EA%B3%A0-%EC%A7%80%EC%97%AD%EC%84%B1
• https://gideokkim.github.io/algorithm%20theory/array/
• https://velog.io/@akfls221/JVM%EC%9C%BC%EB%A1%9C-%EC%8B%9C%EC%9E%91%ED%95%B4-GC-%EA%B7%B8%EB%A6%AC%EA%B3%A0-GC-%ED%8A%9C%EB%8B%9D%EA%B9%8C%EC%A7%80#gcgarbage-collection