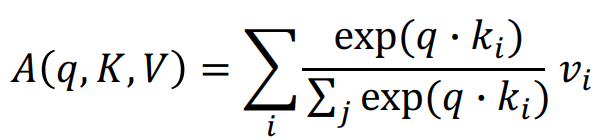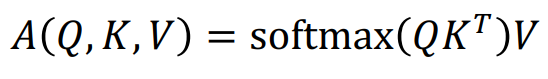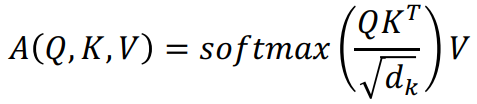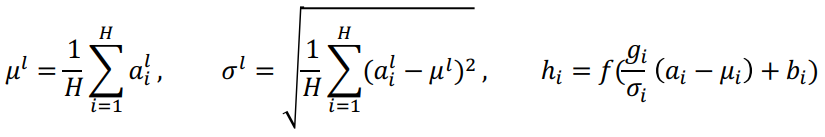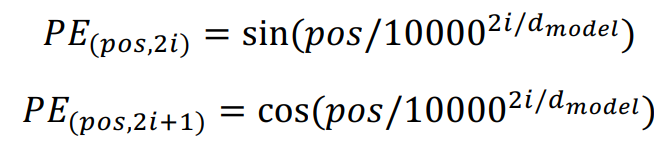Transformer

Transformer

RNN : Long-Term Dependency

• sequence data를 매 time step마다 encoding하는 과정
• $x_t + h_{t-1} → h_t$
• hidden state vector는 해당 time step에서의 input의 정보만 담기는 것이 아니라, 그 전의 input들에 대한 정보들도 함께 담김

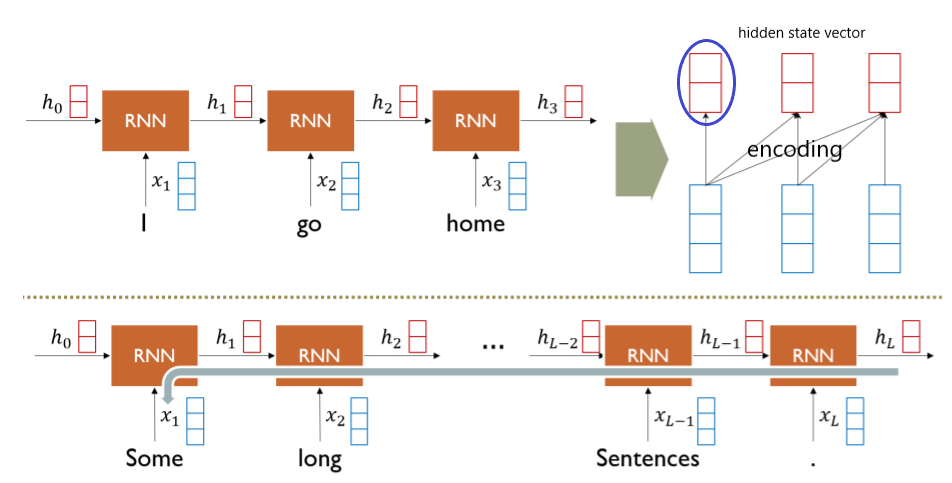
Bi-Directional RNNs

• 왼쪽과 오른쪽의 정보가 같이 포함될 수 있도록 2개의 module을 병렬적으로
• Long Term Dependency 해소위해 사용하나, 성능 향상이 더딤
• Forward RNN (왼쪽에서 오른쪽으로)
  • $h_2^f$ : go 의 왼쪽에 등장했던 단어들의 정보까지를 encoding한 hidden state vector
  • 왼쪽에서 오른쪽으로 encoding하는 RNN module의 특성상, 오른쪽에서 등장하는 단어의 정보 참조해서 I 에 해당하는 encoding vector에 담을 수 없음
• Backward RNN (오른쪽에서 왼쪽으로)
  • 별개의 parameter를 독립적으로 가짐
  • $h_2^b$ : 오른쪽에 등장했던 home 의 정보를 포함한 vector
• Encoding Vector
  • 특정한 time step의 hidden state vector
  • dimension은 hidden state vector의 2배
  • go 가 가지는 sequence 전체적으로의 정보를 고려해서 만듦
  • Forward RNN과 Backward RNN을 거친 결과를 concatenate 수행

Transformer : Long-Term Dependency

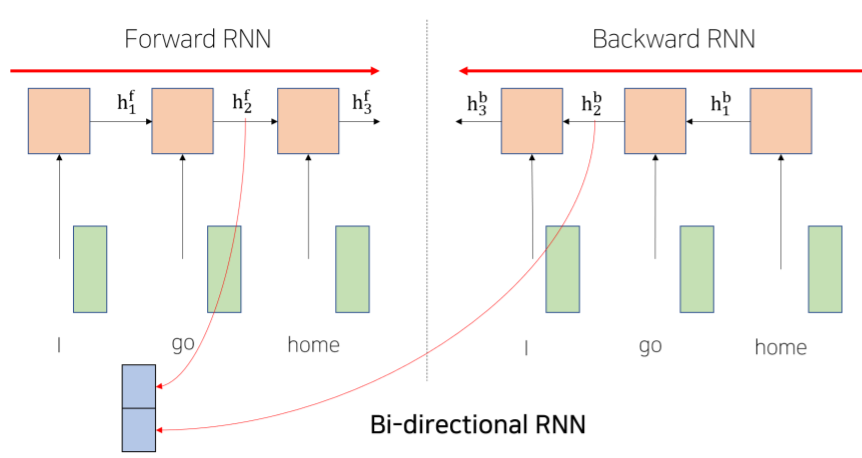
• $x$ : sequence to sequence with attention에서 decoder에서의 특정 time step의 hidden state vector처럼 역할.
  • 찾고자하는 정보를 나타내고 있는 vector
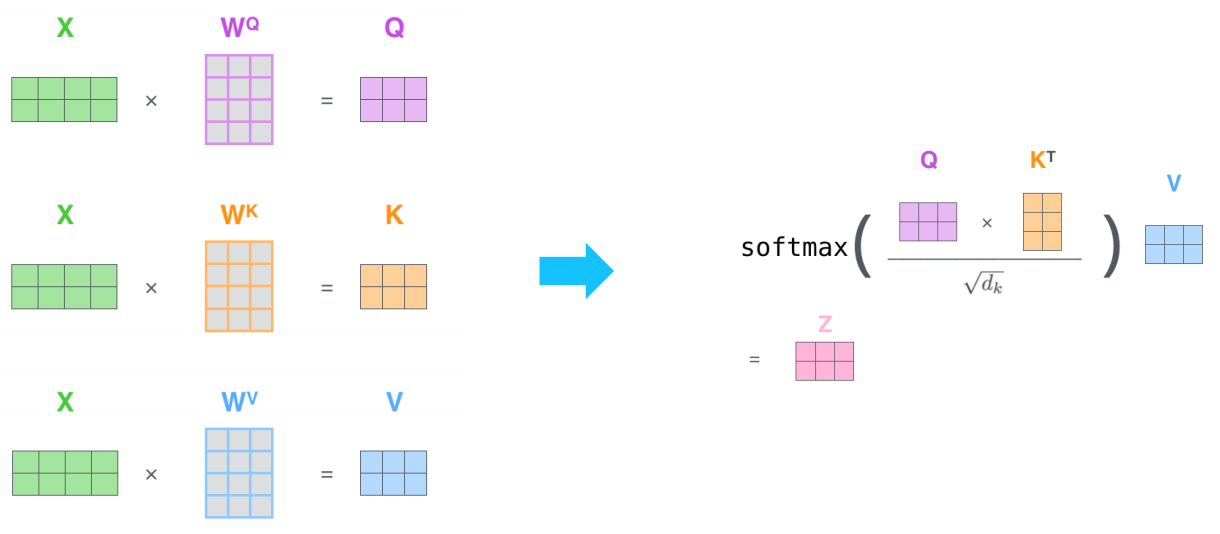
• encoder hidden state vector의 set는 3 개의 vector가 동일하게 사용됨
• $W_Q, W_K, W_V$ : 변환되는 과정에서 사용되는 linear transformation matrix
  • $W_Q$ : 주어진 vector가 query로 변환될 때 사용
  • $W_K$ : 주어진 vector가 key로 변환될 때 사용
  • $W_V$ : 주어진 vector가 value로 변환될 때 사용
• $k$와 $v$는 1대1 대응
• $q, k$에서 attention 연산과정 거쳐 계산된 내적값을 softmax 이용하여 상대적인 가중치로 만들고 상수배 수행
• output vector : sequence 전체 내용을 반영하고 encoding한 결과
  • 입력 vector에 대한 선형 결합/가중 평균을 주어진 I 에 대한 encoding vector로도 고려 가능

• seqeunce 길이가 길어도 self attention module 이용하면 손쉽게 정보 가져올 수 있음
• Queries : 주어진 입력 vector에서 각 입력에 해당하는 word가 decoder hidden state vector인 것처럼 주어진 vector set의 유사도 구하는 형태로 사용. 어느 vector를 가져올지에 대한 기준
• Keys : query vector와 내적이 되는 재료 vector들
• Values : 각각의 key와의 유사도 구하고, softmax 취한 후 가중평균이 구해지도록 하는 재료 vector
  • 본인 스스로 내적했을 때의 값이 커지는 것을 대비하기 위해 사용. input embedding을 그대로 넣지 않은 상태로 attention sore를 구하기 위함
• 원래의 vector와 크기 맞춰주기 위해 $W_Q, W_K, W_V$를 선형 변환 행렬로

• Input vector를 home go I 로 넣어도 최종 encoding vector는 동일한 결과로 나옴
• RNN에서는 sequence를 인식하는 등 순서가 중요하게 여겨지나, Transformer에서는 순서를 무시한 집합으로 보기 때문

Transformer : Scaled Dot-Product Attention

• 입력으로 들어오는 query $q$와 key-value 쌍들 $(k, v)$
• Query, Key, Value와 Output은 모두 vector 형태
• Output은 Value vector에 대한 가중 평균
• 가중 평균에서 사용하는 가중치는 Query vector와 Value vector에 해당하는 Key vector와의 내적값을 통해 구해짐
• Query vector와 Key vector는 내적 연산이 가능해야하므로 같은 차원 $d_k$를 가지고, Value의 차원은 $d_v$
  
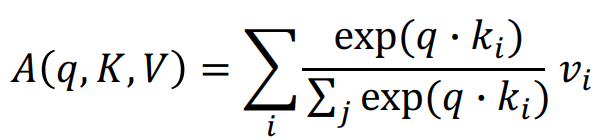
• $A(q,K,V)$ : Attention Module. value vector에 대한 가중평균. $d_v$차원의 vector
• $\frac{exp(q\cdot k_i)}{\sum_jexp(q\cdot k_j)}$ : i번째 key로부터 구해진 softmax를 통과하고 나서의 유사도 값으로, 상대적인 비율을 나타냄

• 확장된 형태
  
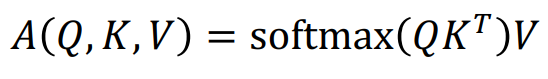
• $A(Q, K, V)$ : 다수의 Query 사용한 Attention Module
• $|Q|, |K|, |V|$는 각각 Query, Key, Value의 개수

• Row-wise softmax : 각각의 row에 대해 softmax 연산 수행
  

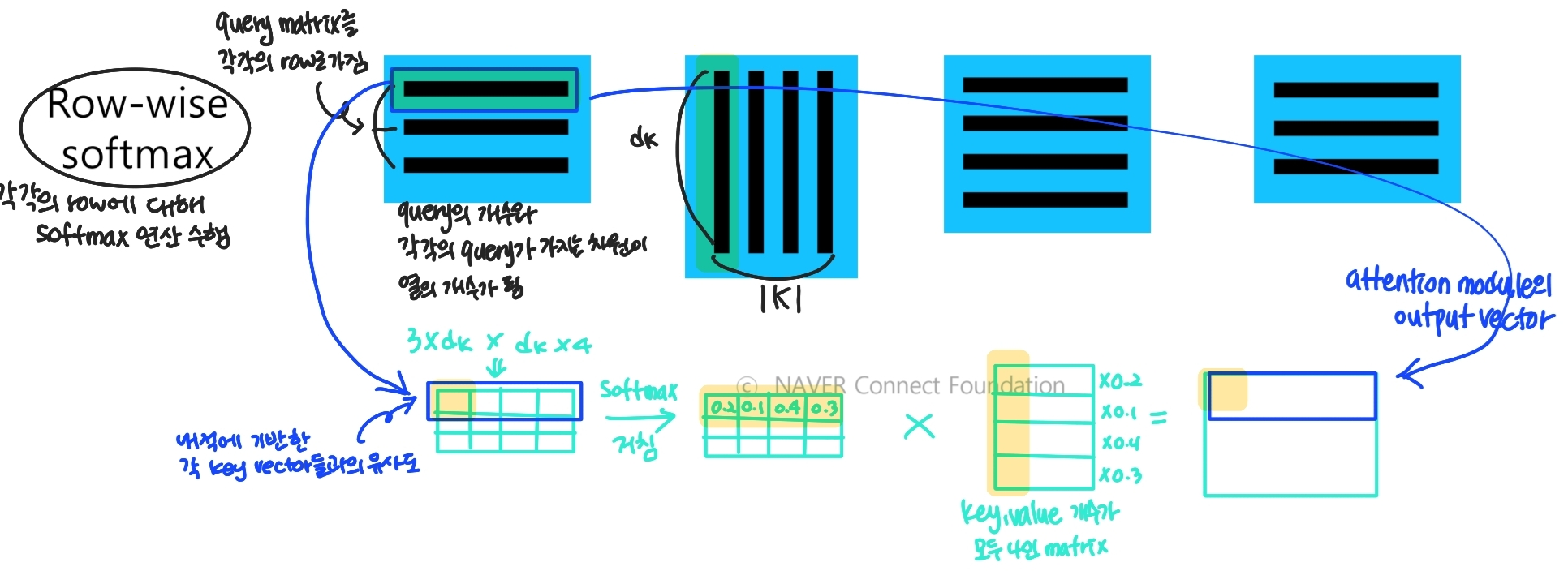
• 그림으로 나타낸 transformer
  
• 왼쪽 그림에서의 오른쪽 $Q, K, V$는 입력 sequence에서 주어진 word 각각에 대한 query, key, value vector
  
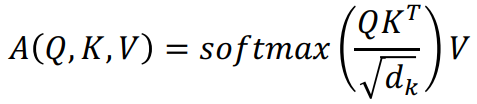
• $d_k$가 커지면서 $q^Tk$의 값이 커지게 됨
• softmax 내의 값들이 커지면 그 결과값도 따라 커질 수 있음
• 이에 따라 gradient 값이 작아지게 됨
• 위의 문제 해결하기 위해 $\sqrt{d_k}$ 사용
  • 평균과 분산값을 유지시켜주기 위해 사용
  • 내적에 참여하는 query와 key의 차원에 따라 내적값의 분산이 좌지우지됨

Transformer : Multi-Head Attention

• self attention module의 확장 version
• 서로 다른 측면의 정보를 병렬적으로 뽑고 그 정보들을 다 merge하는 형태로 attention module 구성
• 각 head가 서로 다른 정보를 상호보완적으로 뽑는 역할 수행
  
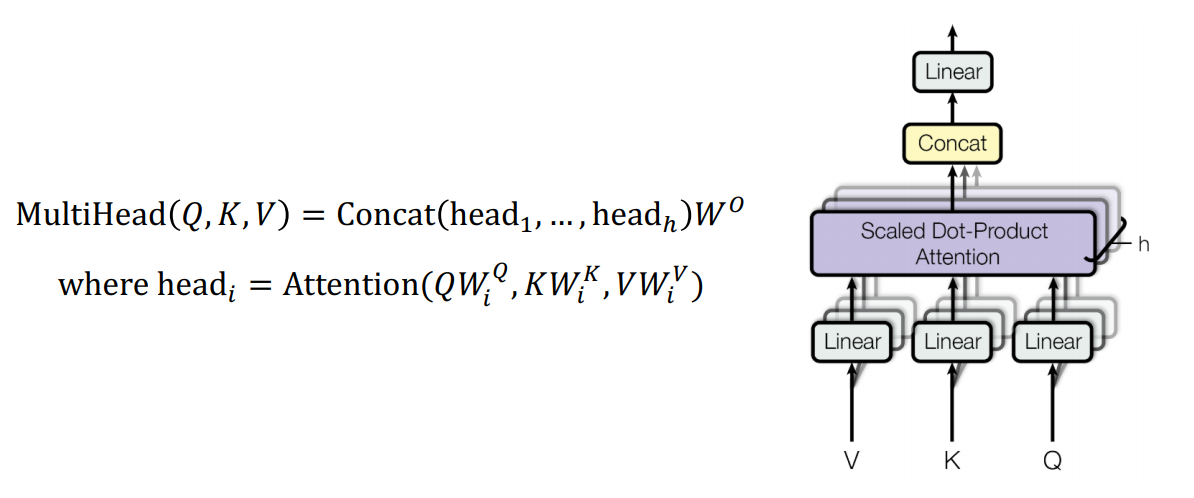
• $QW_i^Q, KW_i^K, VW_i^V$으로 여러 버전의 행렬이 존재
• 오른쪽의 그림에서 Linear는 각각의 $V, K, Q$를 linear transformation 수행하는 과정
• $h$ : 동일한 $V, K, Q$에 대해 동시에 병렬적으로 여러 버전의 attention 수행하는 횟수
• Linear : 해당 query vector에 대한 encoding vector

• 그림으로 나타낸 transformer
  
• 2 단어로 이뤄진 sequence에 대해 2 개의 서로 다른 head 존재 가정
• linear transformation 거친 값이 곧 thinking machine의 encoding vector
  
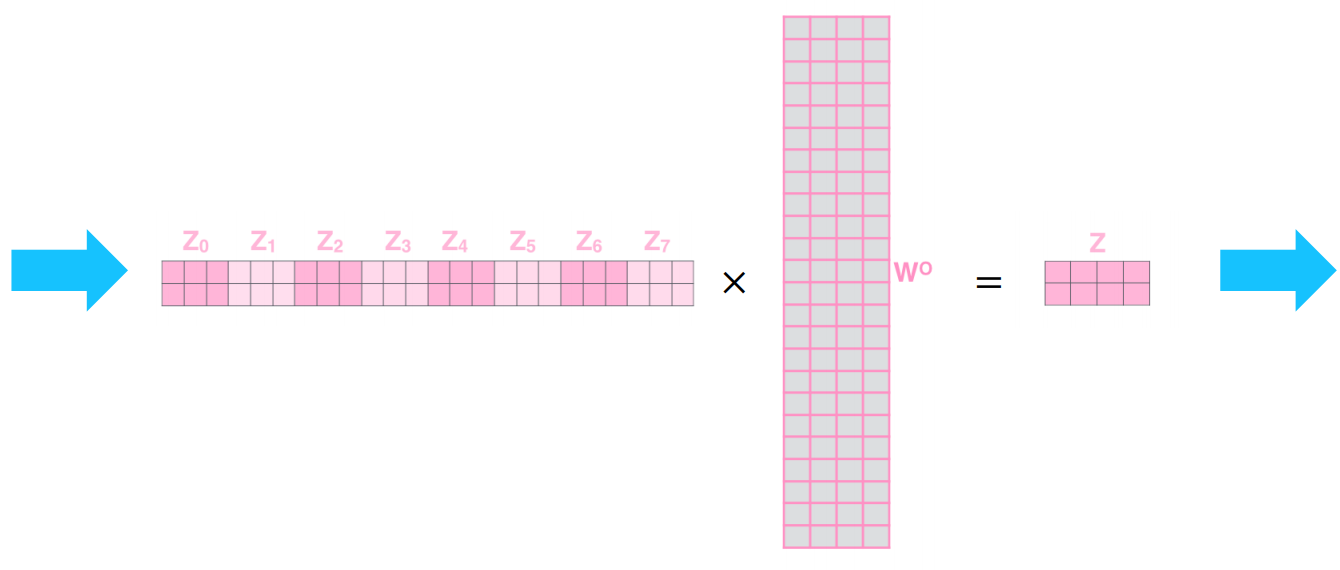
• 이전에 나온 $Z$값들을 모두 concatenate 수행
• query의 개수 == 단어 개수 == thinking machine (2개)
• 각 head에서 나온 value vector 차원 x 총 head의 개수 == 3 x 8 = 24차원
• concat 진행하면서 늘어난 차원을 입력 vector와 맞춰주기 위해 $W^0$으로 linear transformation 수행
  • $W^0$의 차원 = 24 x 4
  • $W^0$의 차원 = concat의 결과로 나온 차원 x 최종적으로 얻으려는 차원
• 최종 $Z$는 직전의 $X$와 같은 dimension 가져야 함

• 다양한 layer type에 대한 Complexity per Layer, Sequential Operations, Maximum Path Length
  
• $n$ : n개의 query와 key에 대한 sequence 길이
• $d$ : 대표하는 차원
• $k$ : convolution의 kernel size
• $r$ : 제한된 self-attention의 size

• Complexity per Layer : 주로 필요로 하는 연산량. 주어진 입력에 따라 가변적
• Sequential Operations : 행렬연산의 병렬화 통해 core 수가 무한히 많다는 가정 아래의 시간복잡도
• Maximum Path Length : Long Term Dependency와 연관

• Self-Attention
  • 모든 key vector들 간의 내적값을 다 가지고 있어야 하기 때문에 많은 memory 요구
  • attention에 기반한 유사도 값이 존재하기 때문에 한 번에 계산 가능
• Recurrent
  • $h_{t-1}$ 계산이 완료될 때까지 기다려야 하기 때문에 시간 복잡도가 높음
  • 가장 끝의 단어가 가장 앞의 단어 참조할 때 어쩔 수 없이 모든 경우를 다 탐색해야 함

Transformer : Block-Based Model

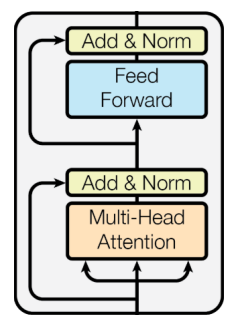
• 각 block에는 두 개의 sub-layer가 존재
  • Multi-head attention
    • 입력값 대비 만들고자 하는 vector의 차이값만을 attention module에서 만들어야 함
  • two-layer feed-forward NN (with ReLU)
• 두 개의 step은 모두 위 그림에서의 add&norm인 Residual connection과 Layer Normalization($LayerNorm(x+sublayer(x))$) 과정을 가지고 있음
  • CV에서 deep layer neural network 만들 때 gradient vanishing 문제를 해결하여 학습을 안정화
  • 이 과정 거치면서 layer 계속 쌓아감에 따라 높은 성능 보일 수 있도록 함
• img 예시
  
  • residual connection 위해 각각의 dimension이 정확하게 일치해야 함

Transformer : Layer Normalization

• 주어진 다수의 sample들에 대해 값들의 평균을 0, 분산을 1로 만들고, 우리가 원하는 평균과 분산을 주입할 수 있도록하는 선형 변환으로 이뤄짐
  
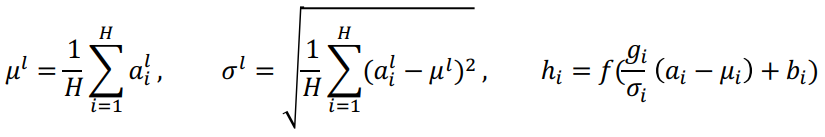
• 예시
• 3, 5, 2 세 개의 값이 주어져있을 때의 평균은 2
• 3-2, 5-2, -2-2 로 각 값을 이전의 평균으로 뺄셈을 계산하여 평균을 0으로 만듦
• $\sqrt{(3-2)^2+(5-2)^2+(-2-2)^2} = \sqrt{26}$
• $\frac{3-2}{\sqrt{26}}$, $\frac{5-2}{\sqrt{26}}$, $\frac{-2-2}{\sqrt{26}}$를 계산하여 표준편차를 1로 만듦
• 만약 이 값들이 $y =$ 2$x$+3에서의 $x$에 들어가면 해당 값들은 평균이 2, 분산이 3 의 값이 됨

• column 방향으로 normalize(standardization) 수행
• row 방향으로 affine transformation 수행
  

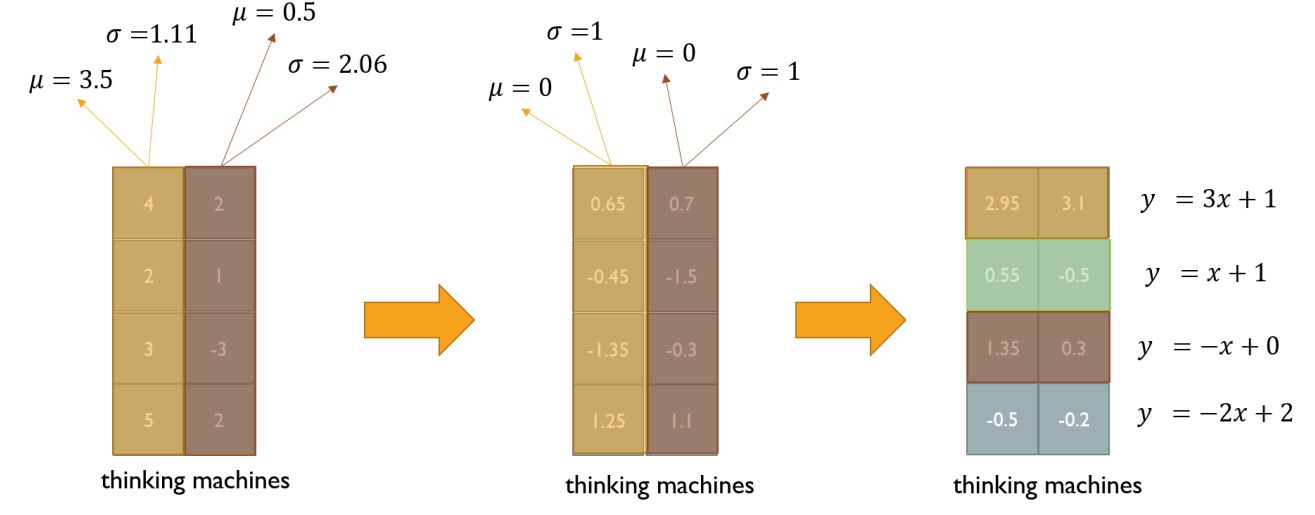
1. row별 평균, 표준 편차 구하기
2. 평균이 0, 표준 편차가 1이 되도록 하기 위해 각 cell의 값 = (이전 cell의 값 - 평균) / 표준 편차 계산
3. 식 $y=ax+b$에서 $x$에 cell 값 주입함으로써 평균이 $a$이고 분산이 $b$인 새로운 값 얻어냄

Transformer : Positional Encoding

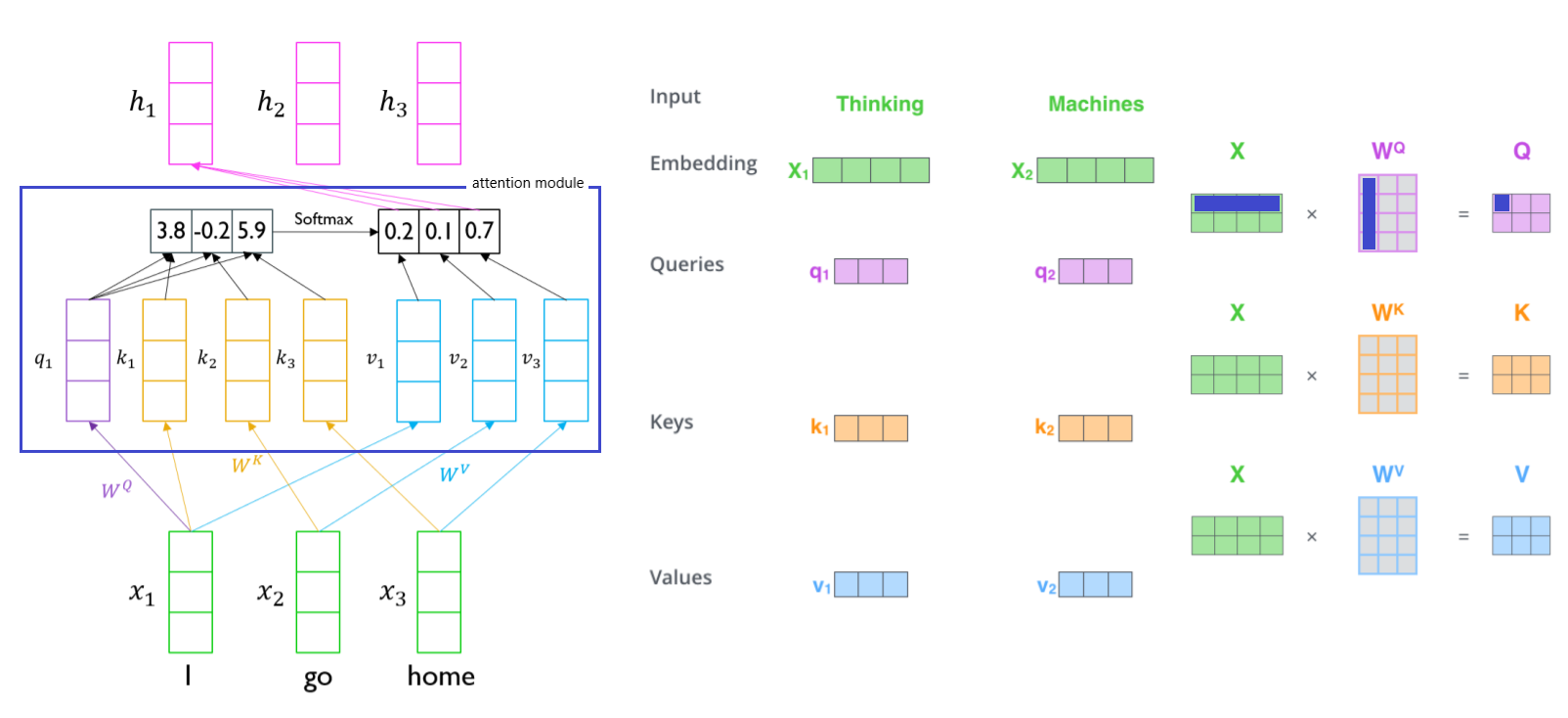
• 서로 다른 frequency 표현하기 위해 주기함수 사용
  
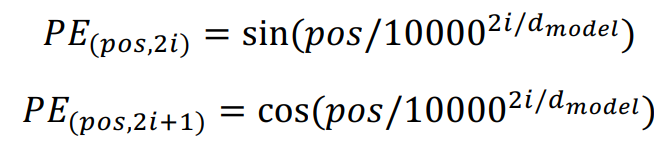
• dimension의 개수에 따라 주기가 달라짐
  
• 순서를 구분하지 못하는 self-attention module의 기본적인 한계점을 위해 위치별로 서로 다른 vector가 더해지도록 함으로써 위치가 달라지면 출력 encoding vector도 달라지도록 함

Transformer : Warm-up Learning Rate Scheduler

• 고정된 값을 사용하는 것보다 최종 수렴 model의 성능을 더 올리는 것을 목적으로, 학습 중에 learning rate의 값을 적절히 변경
  
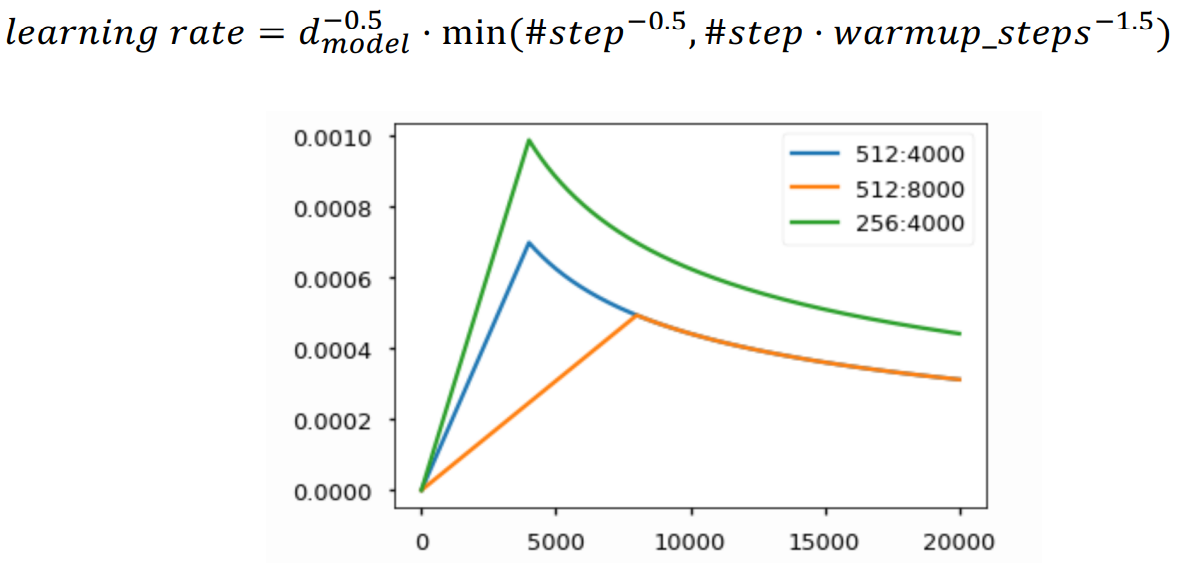
• optimal한 point가 멀리 있을 때 motivation 제공해주고자 $lr$의 값을 크게 사용
  • 보폭이 커서 구하고자하는 지점에 가까워졌을 때 정확한 지점을 찾지 못하고 주변을 맴돌음
• 보폭을 줄이고자 할 때 $lr$ 감소시킴

Transformer : High-Level View

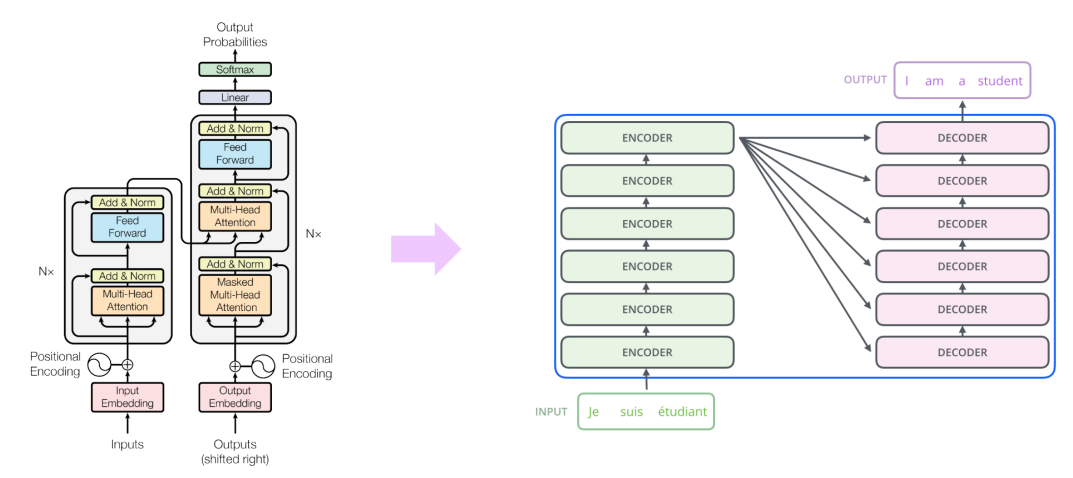
• $N$ : 6, 12, 24, ... 로 동일한 block을 N번 쌓음

Transformer : Encoder Self-Attention Visualization

• 각 단어들이 주변의 다른 단어들과의 연관을 찾고자 함

  

Transformer : Decoder

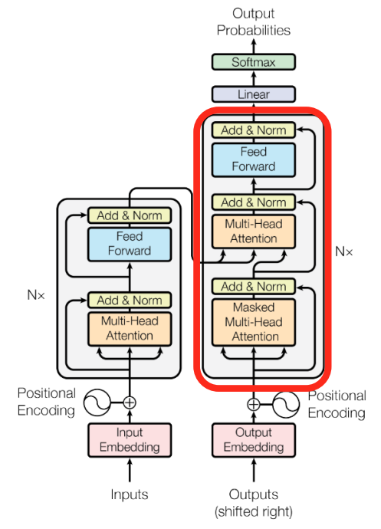
• 빨간색으로 표시된 부분이 Decoder
• Input으로 I go home 이 주어진다면, Output(shifted right)으로는 < SOS > 나는 집에 가 주어짐
• Decoder에서의 Masked Multi-Head Attention과 Add&Norm 부분은 seq2seq에서 decoder의 hidden state vector를 뽑는 과정과 동일
• Multi-Head Attention의 input으로는 encoder에서 주어진 Value, Key, Query vector
• Multi-Head Attention과 Add&Norm은 encoder와 decoder 간의 attention module
• Linear에서는 target language의 vocab size만큼의 vector 생성

Transformer : Masked Self-Attention

• 아직 생성되지 않은 단어들은 inference time동안 접근할 수 없음
• softmax output의 Renormalization은 model이 생성되지 않은 단어에 접근하는 것을 막음
  

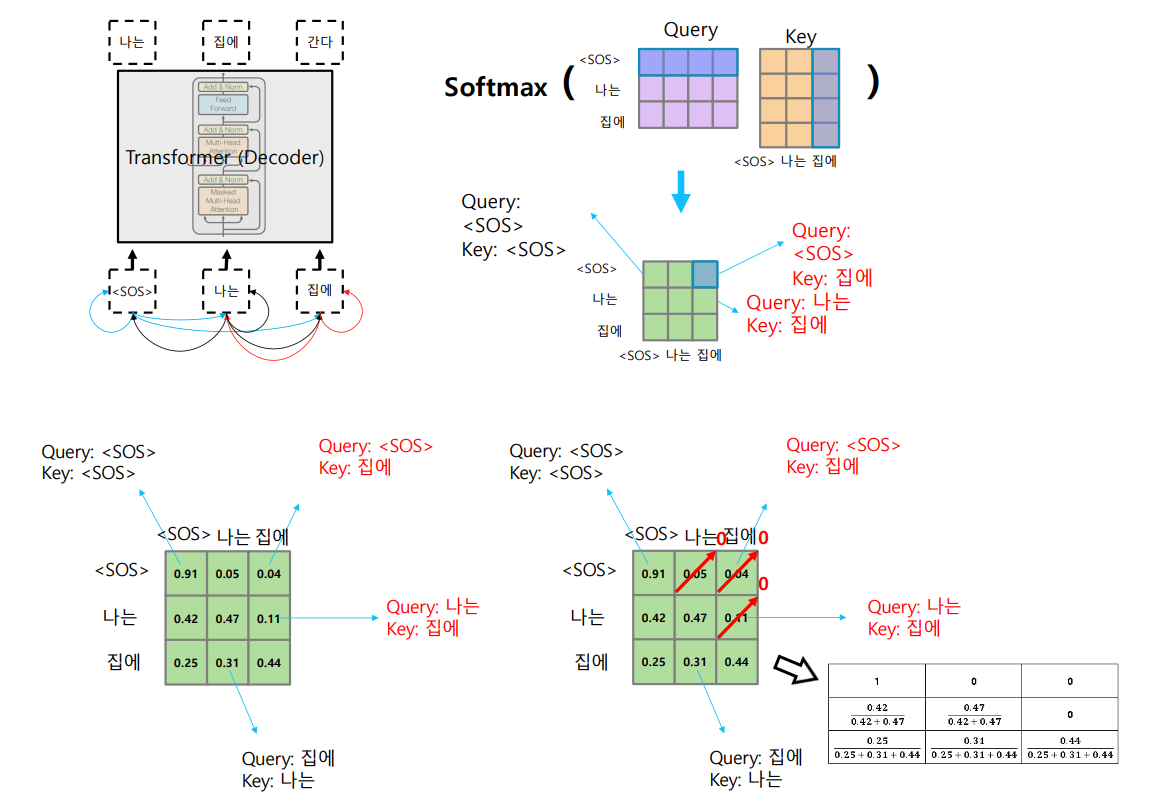
1. 각 단어들 사이마다의 유사도 기록
2. softmax 거치면서 정보를 가져올 수 있는 것들 차단 (다음에 올 단어들 차단)
3. row별로 합이 1이 되도록 normalize 수행