[D+11] Deep Learning Basic

(1) 기초 용어 정리

• 인공지능(Artificial Intelligence): 동적 컴퓨팅 환경 내에 내장된 알고리즘을 생성하고 적용하여 인간의 지능을 모방하는 기초적인 지능
  

• 손실함수(loss function): 모델의 예측값과 실제값 사이 차이를 수식화한 함수

• 최적화(optimization): 손실함수 값을 어떻게 감소시킬 것인지에 대한 방법론

• 일반화(Generalization): 학습 데이터와 테스트 데이터에 대한 예측 성능이 유사할수록 일반화 성능이 좋다고 표현, 즉 Overfitting이 일어날 때는 일반화 성능이 저하된 것으로 해석할 수 있음

• 과소적합(Underfitting): 모델이 너무 작거나 epoch이 너무 적어서 학습이 제대로 이루어지지 않음

• 과대적합(Overfitting): 학습 데이터에 대해 모델의 파라미터가 너무 맞춰져서 오히려 테스트 데이터에 대해서는 성능이 좋지 않음

• 교차 검증(Cross Validation): 학습 데이터를 k개의 뭉치로 분할하여, k-1 개는 학습하고 1개는 검증에 사용하는 방식을 k번 반복하여 모델의 파라미터를 최적화

• 편향(Bias): 평균적으로 값이 실제 값과 유사하면 low, 다르면 high

• 분산(Variance): 입력에 대한 출력이 얼마나 일관적인지를 보여줌. 비슷한 입력에 대해 출력의 차이가 유사하면 variance가 작으며, 차이가 크다면 variance가 크다고 볼 수 있음.

  • 이때 편향과 분산은 서로 trade-off 관계로 둘 다를 동시에 줄일 수는 없음

• Bootstrapping: 학습 데이터의 일부를 사용해 모델을 여러 개 만들고, 각각의 모델이 예측하는 값이 얼마나 일치하는가를 확인

  • Bagging: 학습 데이터의 일부를 학습시킨 여러 개의 모델을 함께 사용(Parallel)
  • Boosting: 작은 모델로 예측하여 예측이 틀린 데이터에 대해 예측하는 모델을 또 만들고, 이런 식으로 연쇄적으로 모델을 사용(Sequential)
    
    

(2) Neural network & MLP(Multi Layer Perceptron)

• 신경망(Neural Network)

  • 신경망 = 함수, 선형 & 비선형 연산이 연속적으로 일어나는 함수

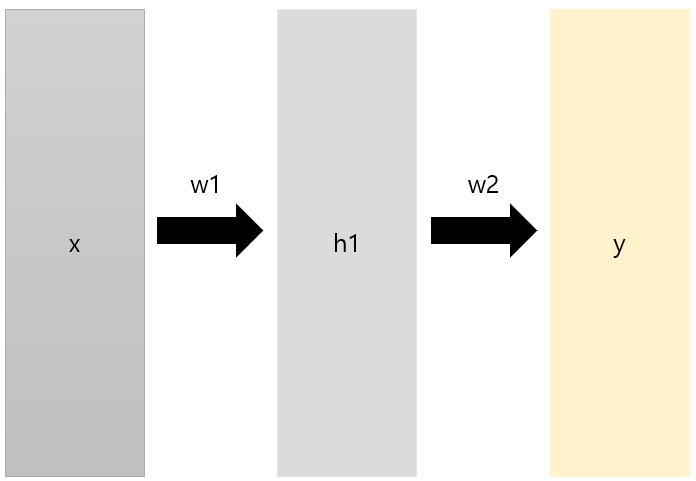
• 다층 퍼셉트론(Multi Layer Perceptron): 퍼셉트론 여러 층으로 구성

  • Perceptron
  

  • $Data : {(xi, yi)}$ , $i = 1,2,...,N$

  • $Model : y=W^T X+b$

  • $Loss$
    

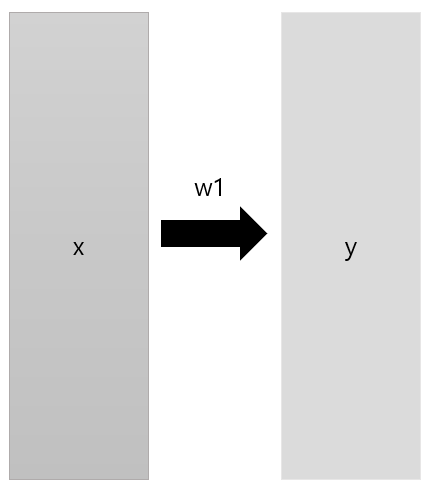
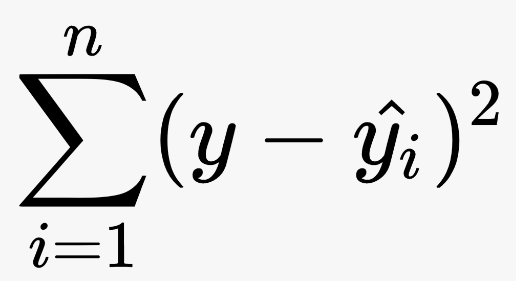
  • 위 Model 식까지만 전개하면 선형성만 있기 때문에 네트워크의 표현력이 제한됨. 비선형성을 추가함으로써 표현력을 극대화할 수 있기 때문에 활성화 함수를 사용함

  • Multi Layer Perceptron은 위 Perceptron이 여러 층 모인 구조
  
  • $y = W_2^T h_1= W_2^T ρ(W_1^T X)$

(3) Loss function & Optimization

• Loss function

  • 회귀 문제

  

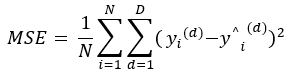
  • 분류 문제

    

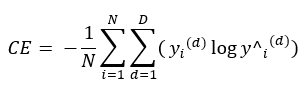
  • 확률 문제

    

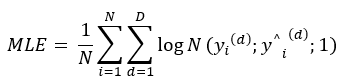
• Optimization

  • Gradient Descent Algorithm

    : Local Minimum을 찾는 방법론

    • Stochastic Gradient Descent

      $W_(t+1) := W_t - ng_t$

      n: 학습률

    • Momentum

      $a_(t+1) := βa_t + g_t$

      💫 SGD의 느린 수렴 속도 -> "이전 파라미터의 학습 방향으로 보통 향하지 않을까?"

      라는 아이디어에서 출발하여 이전 파라미터 값에 β만큼 곱하여 이전 정보까지 활용해 파라미터 업데이트

    • Nesterov Accelerated Gradient

      $α_(t+1) ∶= βα_t+∇L(W_t-nβα_t)$
      $W_t := W_t - a_(t+1)$

      💫 Momentum의 관성 때문에 local minimum에 수렴하는 데에 오히려 좀 느림
      -> "모멘텀 방향으로 이동한 곳에서의 기울기를 반영한다면?"

      모멘텀 방향으로 먼저 이동을 한 후에, 그 곳에서의 기울기를 구해 파라미터 업데이트

    • Adagrad

      $W_(t+1) := W_t -$$n \over (G_t + e)^(1/2)$$g_t$

      $G_t$: Gradient Squares의 합

      🌟 이미 많이 파라미터 업데이트가 이루어졌다면 적게 변하고, 파라미터 업데이트가 적게 이루어졌다면 크게 변화

    • Adadelta

      $G_t := rG_(t-1) + (1-r)g_t^2$

      $W_(t+1) := W_t -$$(H_(t-1) + e)^(1/2) \over (G_t + e)^(1/2)$$g_t$

      $H_t := rH_(t-1) + (1-r)∆W_t^2$

      Adagrad에서 학습이 진행됨에 따라 기울기가 소실되는 문제를 방지하려고 나왔지만,

      learning rate같이 파라미터 업데이트에서 영향을 미칠 수 있는 사용자가 직접 조정할
      하이퍼파리미터가 없어 잘 사용하지 않음

    • RMS Prop

      $G_t := rG_(t-1) + (1-r)g_t^2$

      $W_(t+1) := W_t -$$n \over (G_t+e)^(1/2)$$g_t$

      Adagrad에서 step size를 추가(learning rate n)

    • Adam

      $m_t := β_1m_(t-1) + (1-β_1)g_t$

      $v_t := β_2v_(t-1) + (1-β_2)g_t^2$

      $W_(t+1) := W_t -$$n \over (G_t+e)^(1/2)$$(1-β_2^t)^(1/2) \over (1-β_1^t)$$g_t$
      
      

    어떤 optimizer를 선택해서 학습을 시키느냐에 따라 같은 모델이더라도 학습 수렴 속도에 많은 영향을 미치기 때문에 효율적인 면에서 영향이 굉장히 크다고 볼 수 있다.
    보통 많이 사용하는 optimizer는 adam으로 평균적으로 괜찮은 성능을 보인다.