Logistic Regression

Linear Regression

• Basic machine learning and statistical analysis method, which assumes the linear relationship between input and output
• We estimate the optimal coefficients to minimize the loss function

Logistic Regression

• Categorical Variable
  - Binary(0, 1)
  - Multi-class(1, 2, 3)
• Different approach to simple linear regression is required
  

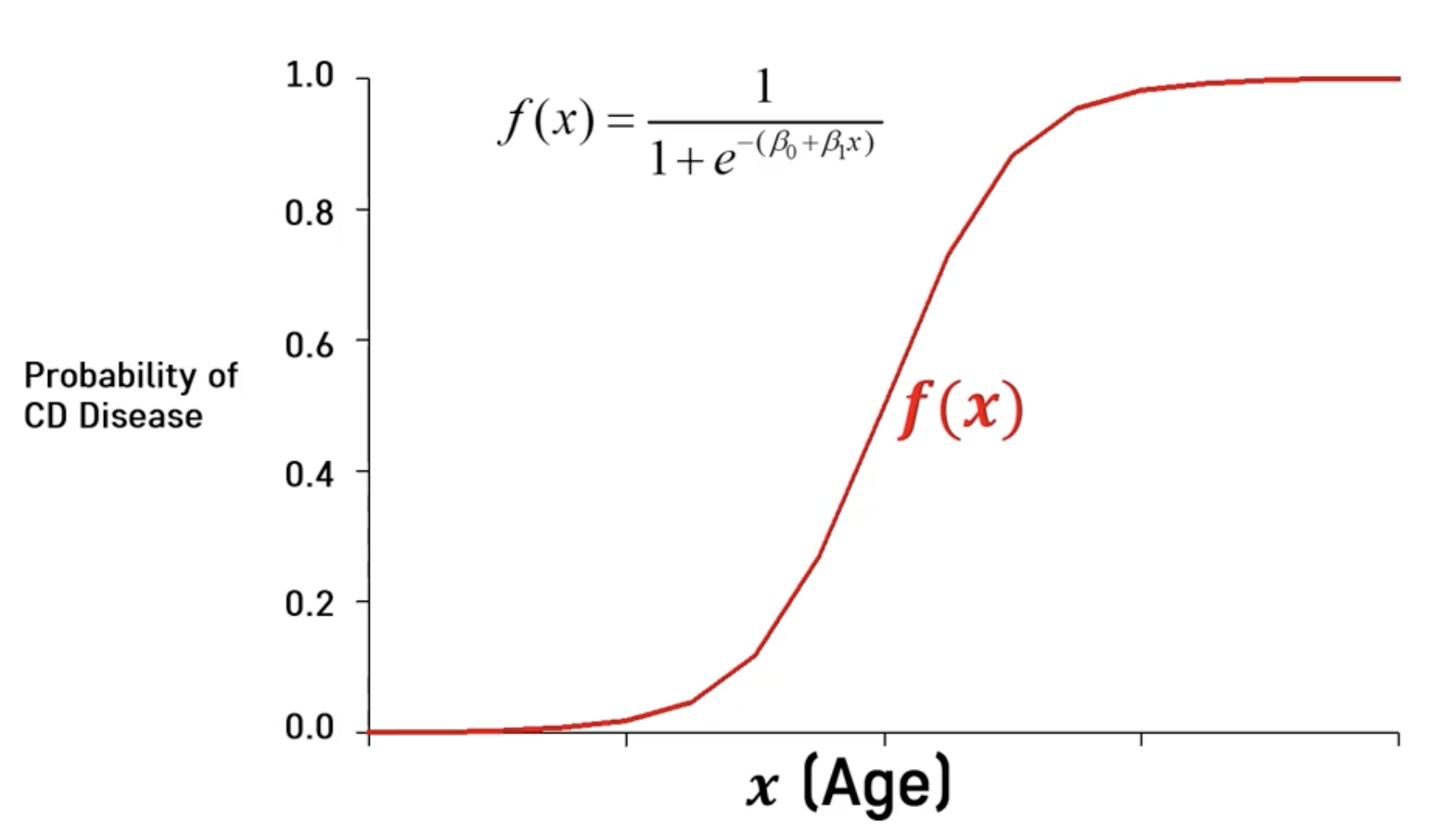
➡️ Sigmoid 함수

• Minimize Loss(=Cross-Entropy)

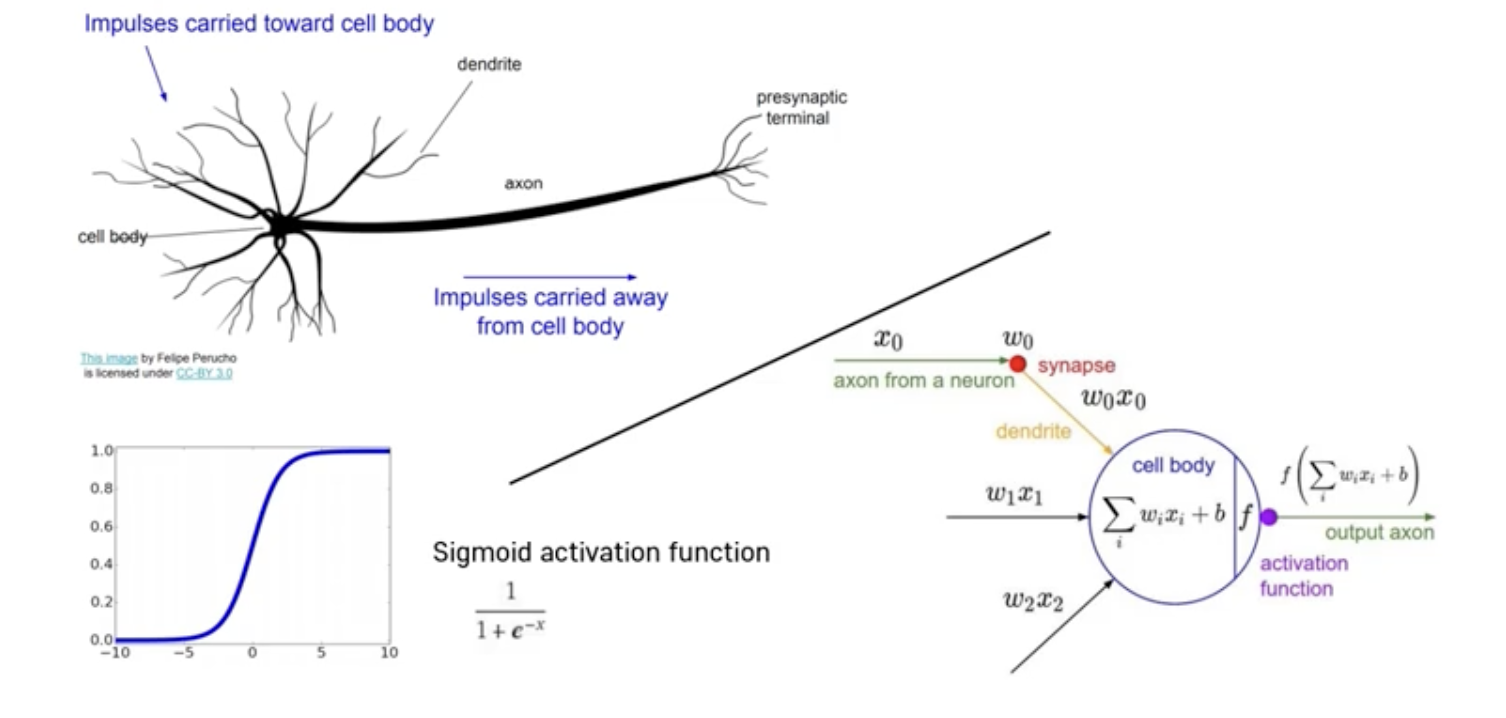
Neuron and Logistic Regression

• A Logistic Regression model (Perceptron) corresponds to a neuron in our brain
  

Limitation of Linear Classifier

• Basic logistic regression model is unable to classify nonlinear patterns
• We must transform our data to be appropriate for linear classifier
  = Finding better data representation manually
  

➡️ 같은 데이터이지만 표현 방식에 따라 분류가 달라짐

Basic Structure

Logistic Regression to Neural Network

• If we stack linear classifiers, we can automatically learn the nonlinear pattern

Linear Regression

➡️ 입력에 대한 parameter을 곱하는 선형적인 표현
➡️ Y = XB
x -> Data Metrix
B -> coefficient vector

Logistic Regression

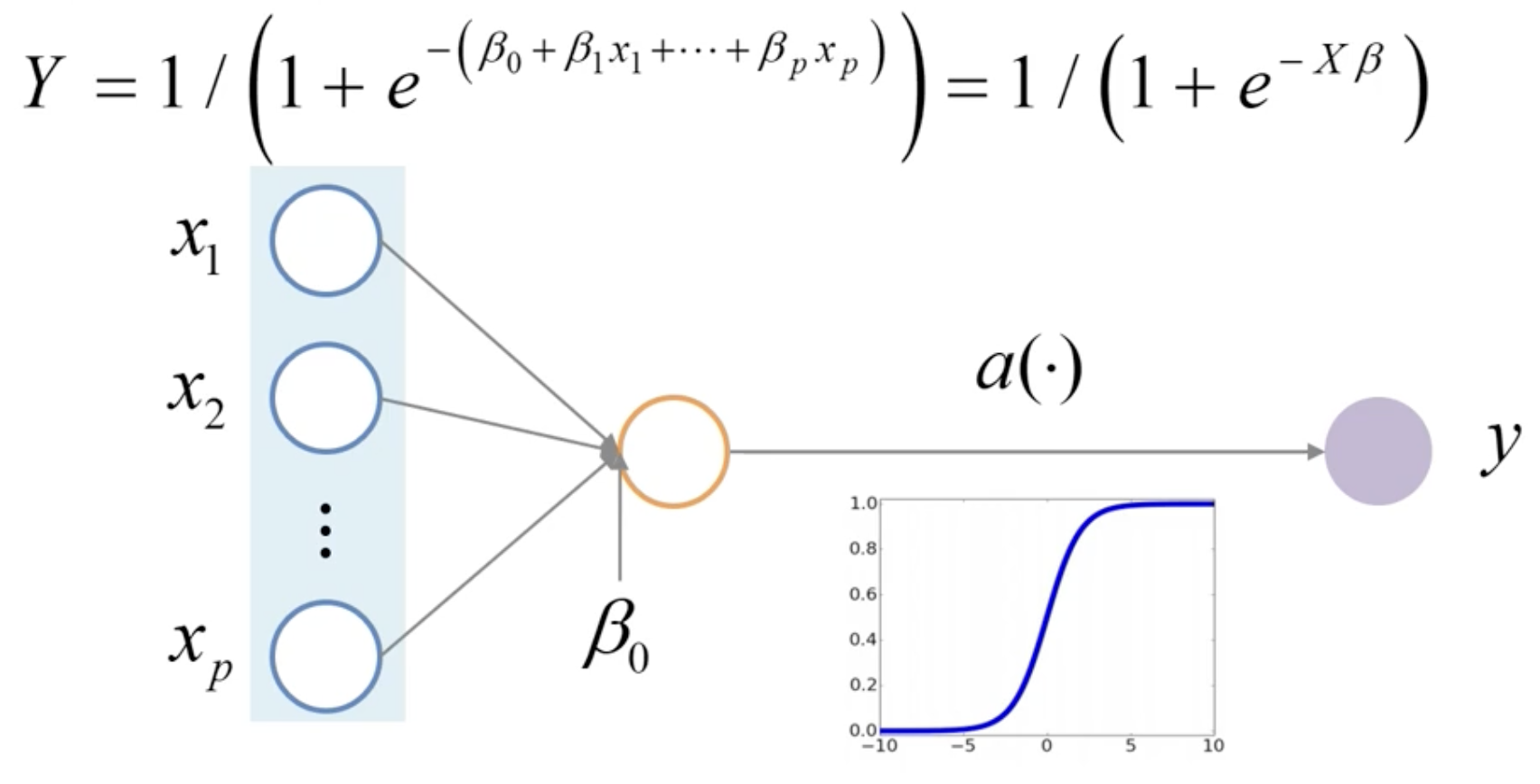
➡️ 선형함수를 시그모이드 함수(Activation Function) 에 넣어서 그 값을 비선형적으로 변환해주는 함수

Multi-output Linear Regression

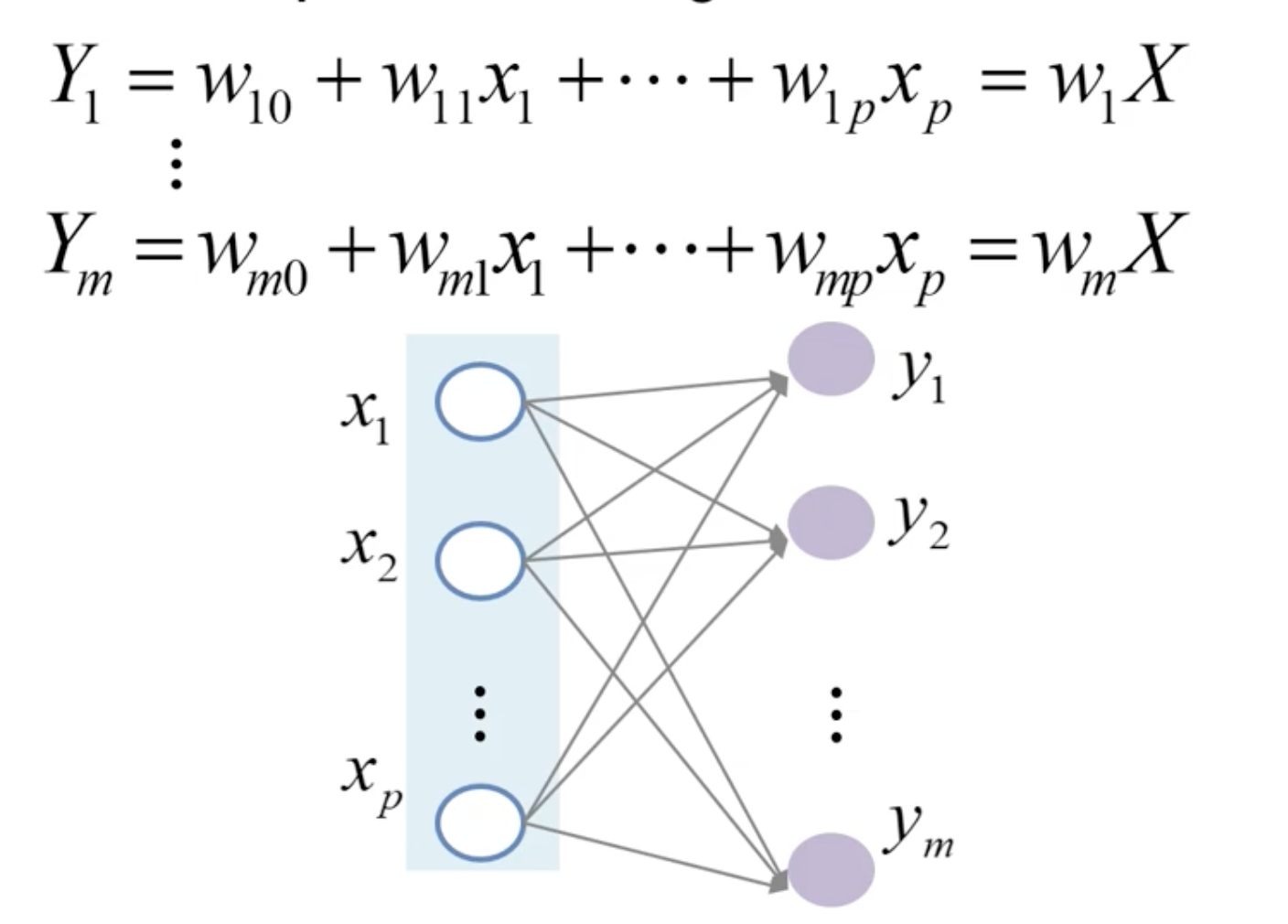
➡️ 1개의 input에 대해 output이 여러개로 출력

2-Hidden Layer Neural Network

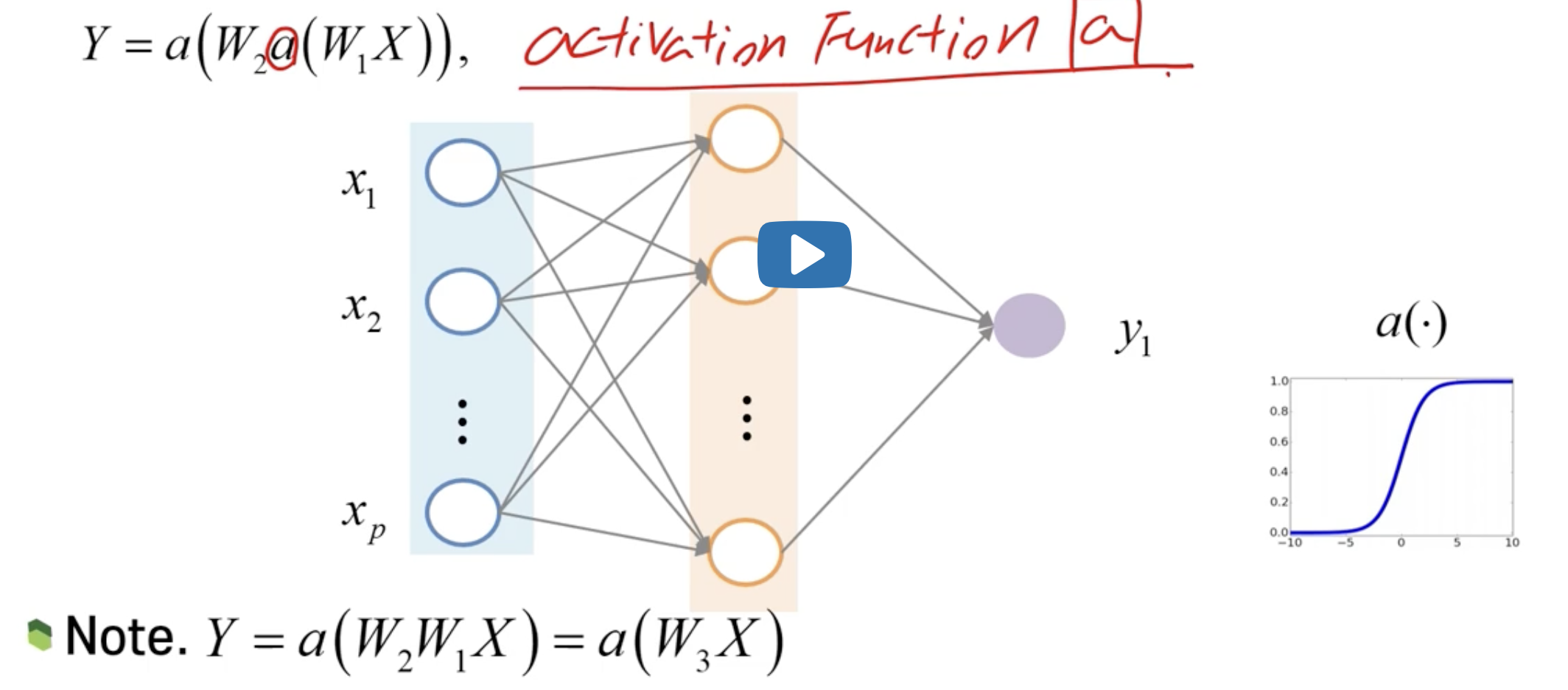
➡️ hidden layer 중간에 삽입된 Activation Function의 중요성
: 여러 층의 비선형적 패턴을 스스로 학습한다의 최종 목적을 달성하기 위해서

Multi-layered Structure

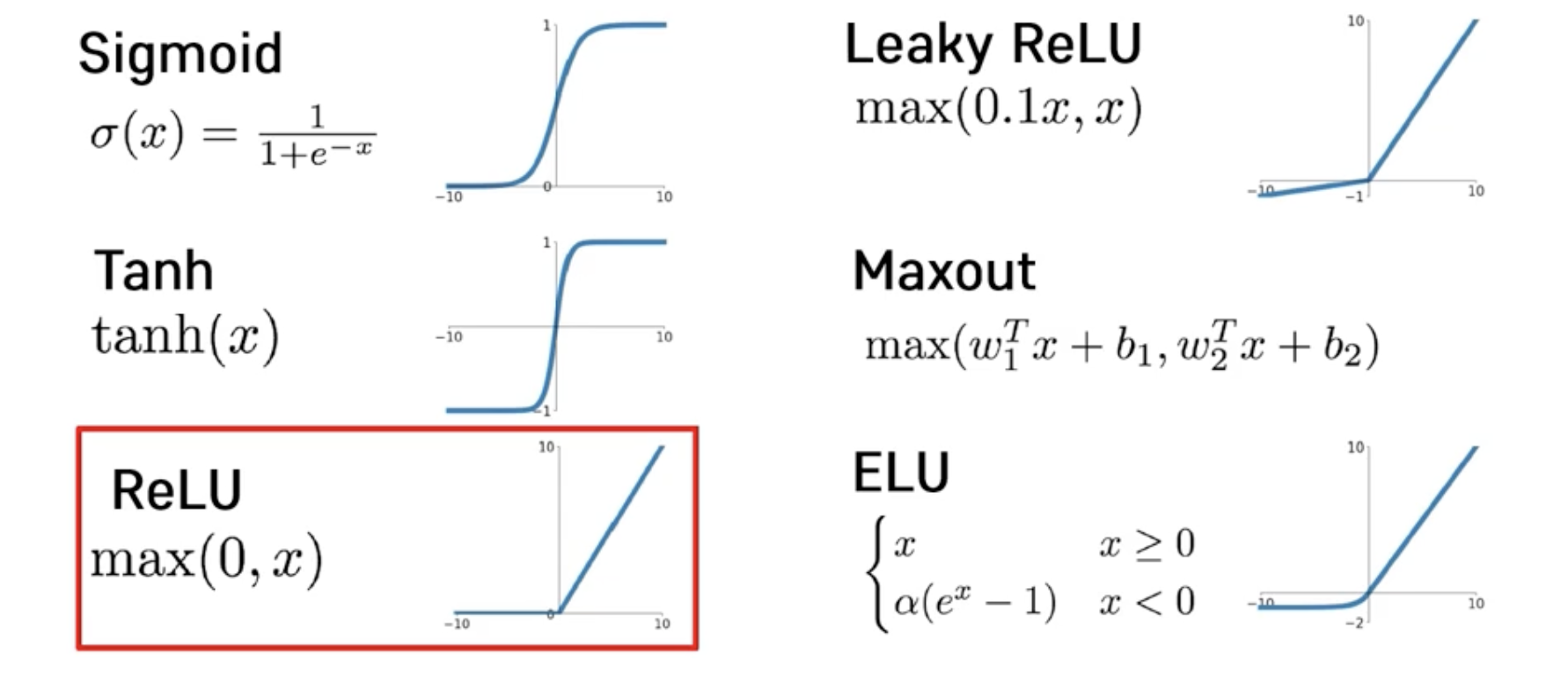
Activation Functions

• Sigmoid
• Tanh
• ReLU
  ➡️ max(0,x)
  ➡️ 0보다 크면 x 출력, 0보다 작으면 0 출력
  ➡️ 최근에 많이 사용
• Leaky ReLU
  ➡️ max(0.1x, x)
• Maxout
• ELU
  ➡️ 문제점 : activation이 안될경우, 그 다음부터 학습 진행이 안됨
  

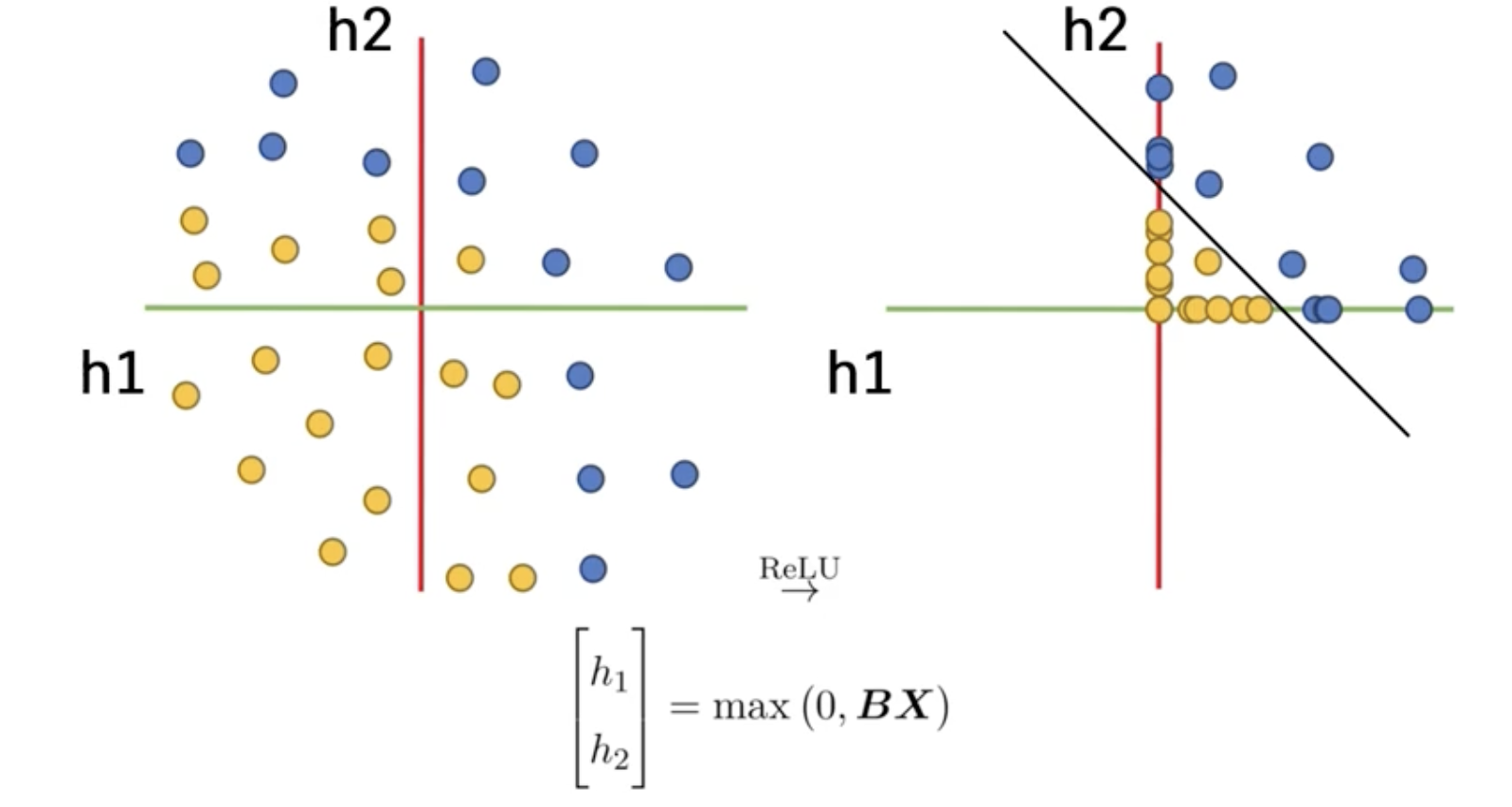
how activation functions work (ReLU)

➡️ x1, x2 에서 h1, h2를 기준으로 하는 새로운 데이터 공간
➡️ 특정 직선이나 평면을 대변하는 벡터에 데이터벡터를 내적
➡️ 새로운 기준축이 되는 관점으로 기존의 데이터 축을 바라보겠다.
➡️ 선형 파라미터들 곱해주는 작업은 새로운 좌표공간으로 기존 데이터들을 선형변환 시켜줌

➡️ 각각의 h1, h2축 기준으로 봤을 때 0보다 작은 값들은 다 0으로 만들어준다
➡️ 1사분면을 제외한 2, 3, 4사분면의 값들의 변화

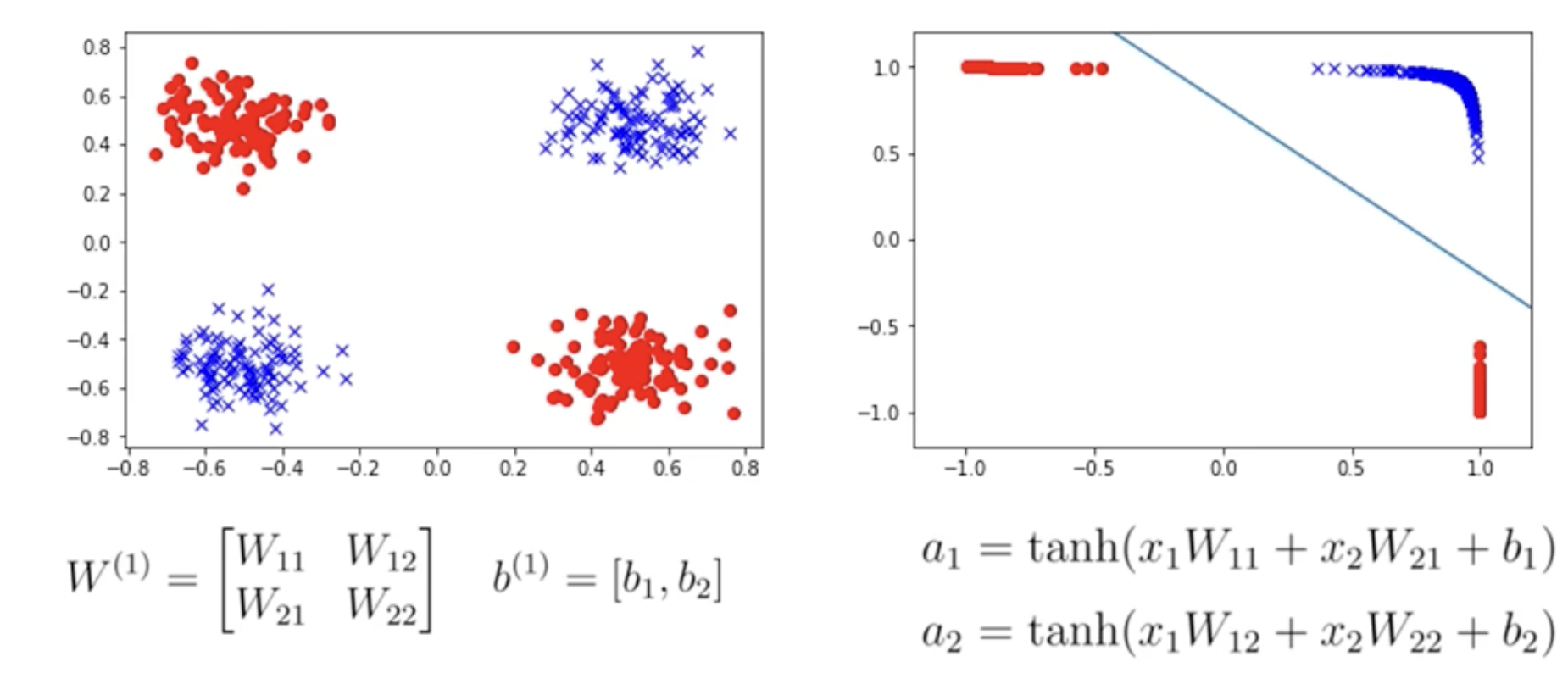
how activation functions work (tanh)

Softmax Function

how to Train Neutral Network

• Minimize Loss(Cross-Entropy)

reference : K-MOOC 실습으로 배우는 머신러닝