Clustering 군집화

: 유사한 속성들을 갖는 관측치들을 묶어 전체 데이터를 몇 개의 개인 군집(그룹)으로 나누는 것

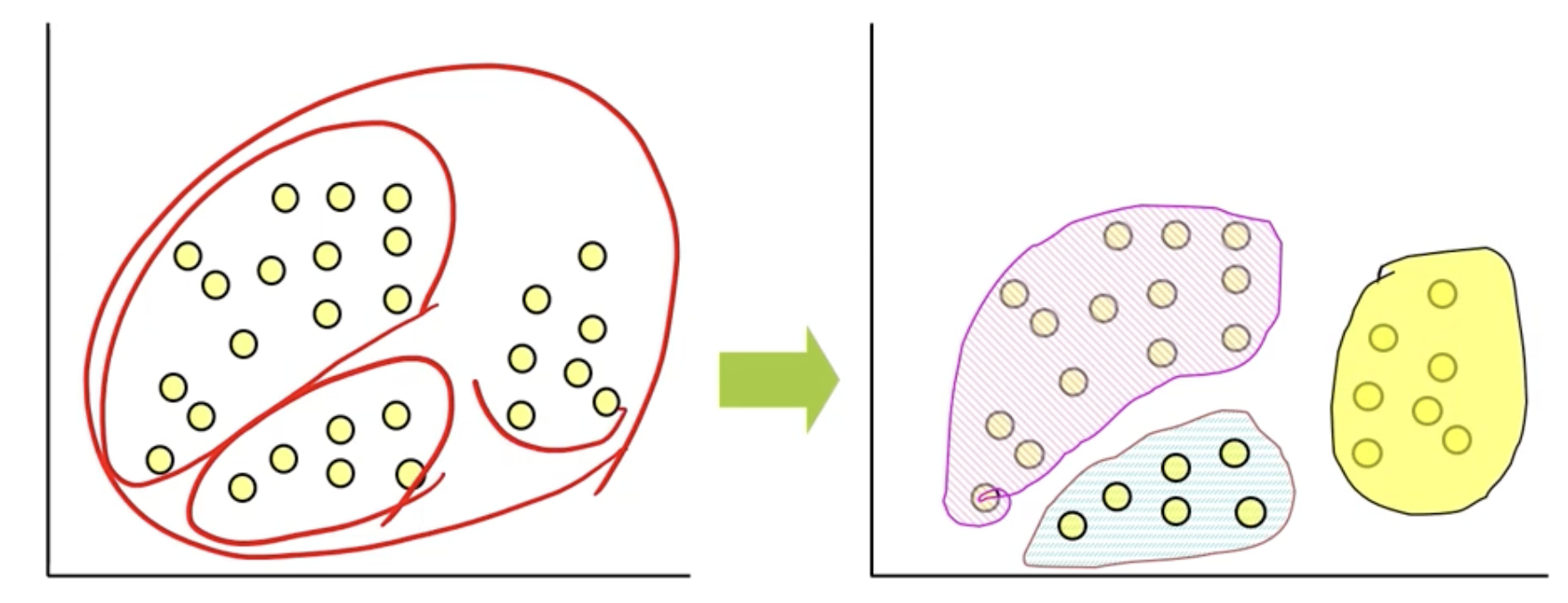
군집화의 기준

• 동일한 군집에 속한 관측치들을 서로 유사할수록 좋음
• 상이한 군집에 속한 관측치들은 서로 다를수록 좋음

분류(Classification) vs. 군집화(Clustering)

• 분류 : 사전에 정의된 범주가 있는 (labeled) 데이터로부터 예측 모델을 학습하는 문제
  ➡️ Supervised Learning
• 군집화 : 사전 정의된 범주가 없는 (unlabeled) 데이터에서 최적의 그룹을 찾아나가는 문제
  ➡️ Unsupervised Learning
  

적용사례

1. 특성 별 고객 군집
   (Customer Segmentation)
   ➡️ Segmentation, Targeting, Positioning
   

2. 유사 문서 군집화
   

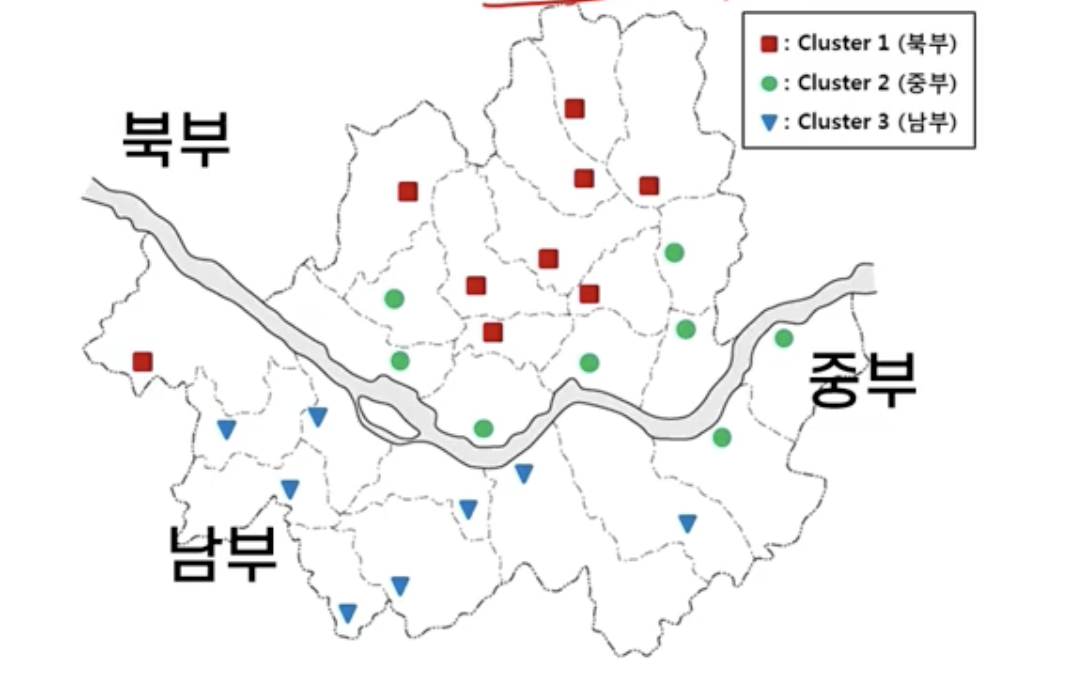
3. 서울시 오존 농도, 미세먼지의 패턴 군집화(25개 구)
   

4. 반도체 웨이퍼의 fail bit map 군집화
   

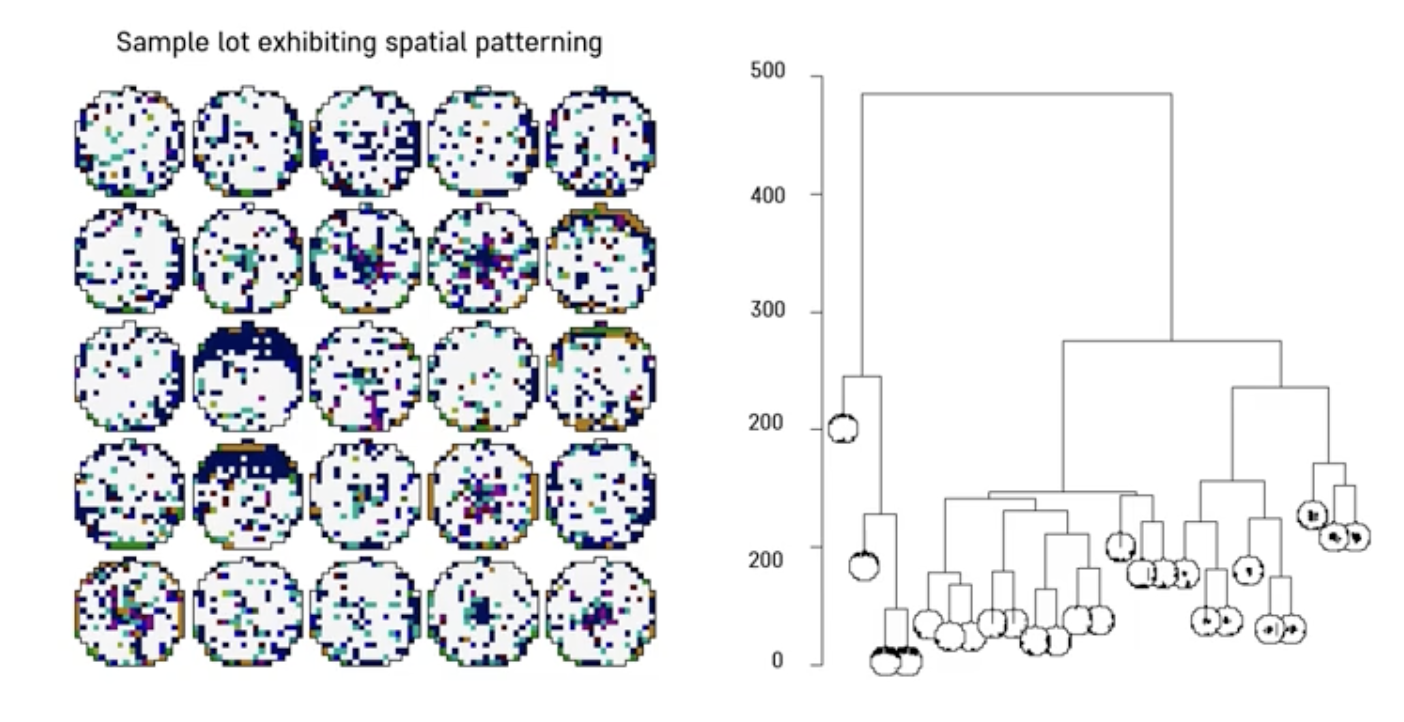
군집화 유사도 척도

어떤 거리 척도를 사용하여 유사도 측정 할 것인가?

• 유클리디안 거리 (Euclidean Distance)
• 맨하탄 거리 (Manhattan Distance)
• 마할라노비스 거리 (Mahalanobis Distance)
• 상관계수 거리 (Correlation Distance)

유클리디안 거리 Euclidean Distance

• 일반적으로 가장 많이 사용하는 거리 척도
• 서로 다른 관측치 x, y 값 간 차이 제곱합의 제곱근
  (= 두 관측치 사이의 직선거리)
  

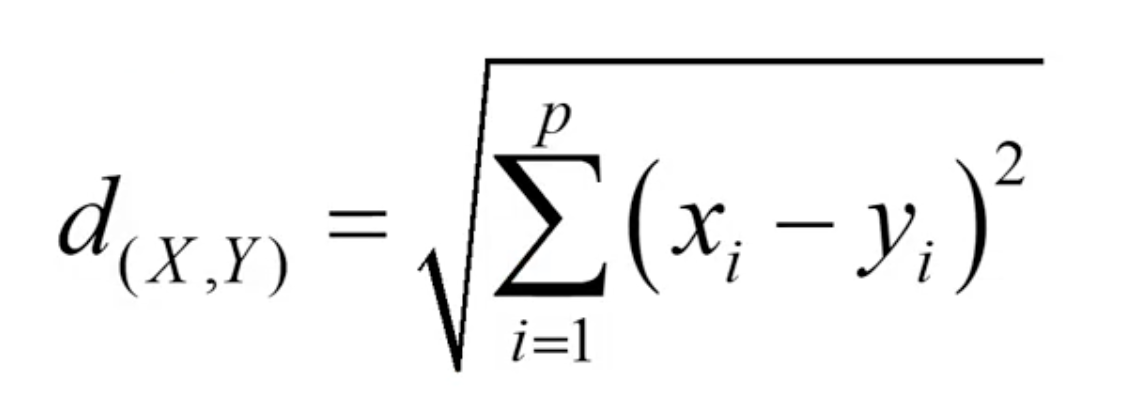
• 2차원에서 두 관측치 사이의 거리는?
  

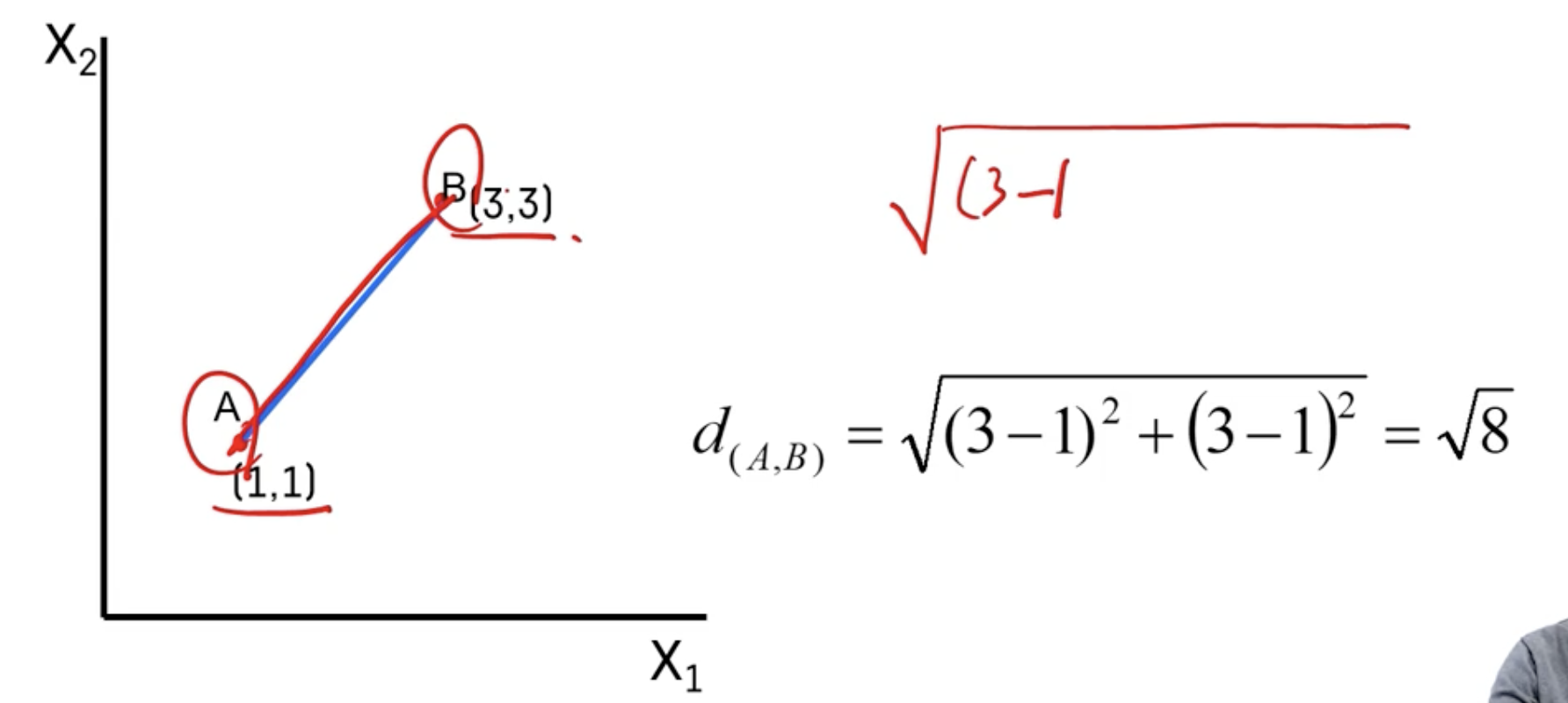
• 3차원에서 두 관측치 사이의 거리는?
  ➡️

맨하탄 거리 Manhattan Distance

• X에서 Y로 이동 시 각 좌표축 방향으로만 이동할 경우에 계산되는 거리
  

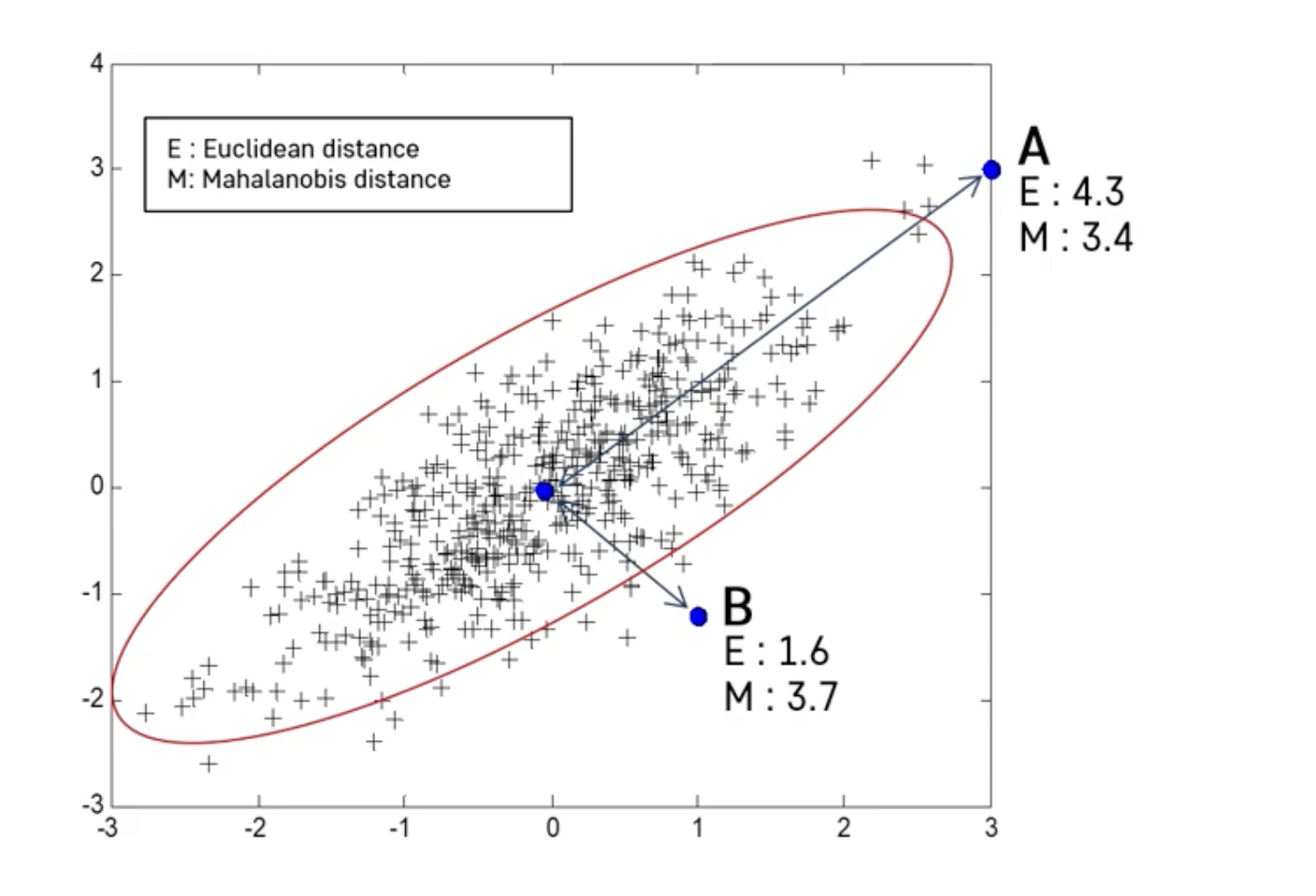
마할라노비스 거리 Mahalanobis Distance

• 변수 내 분산, 변수 간 공분산을 모두 반영하여 X, Y 간 거리를 계산함
• 데이터의 공분산행렬이 단위행렬일 경우 유클리디안 거리와 동일함
  
  

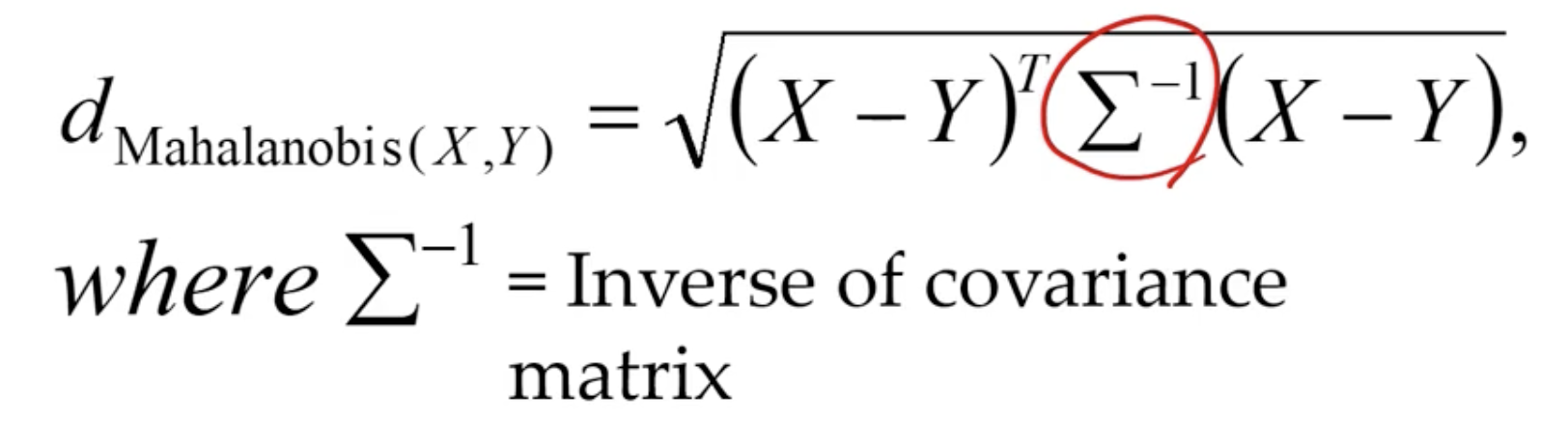
상관계수 거리 Correlation Distance

• 데이터 간 Pearson correlation 값ㄷ을 거리 척도로 직접 사용함
• 데이터 패턴의 유사도 및 비유사도르 반영할 수 있음
  
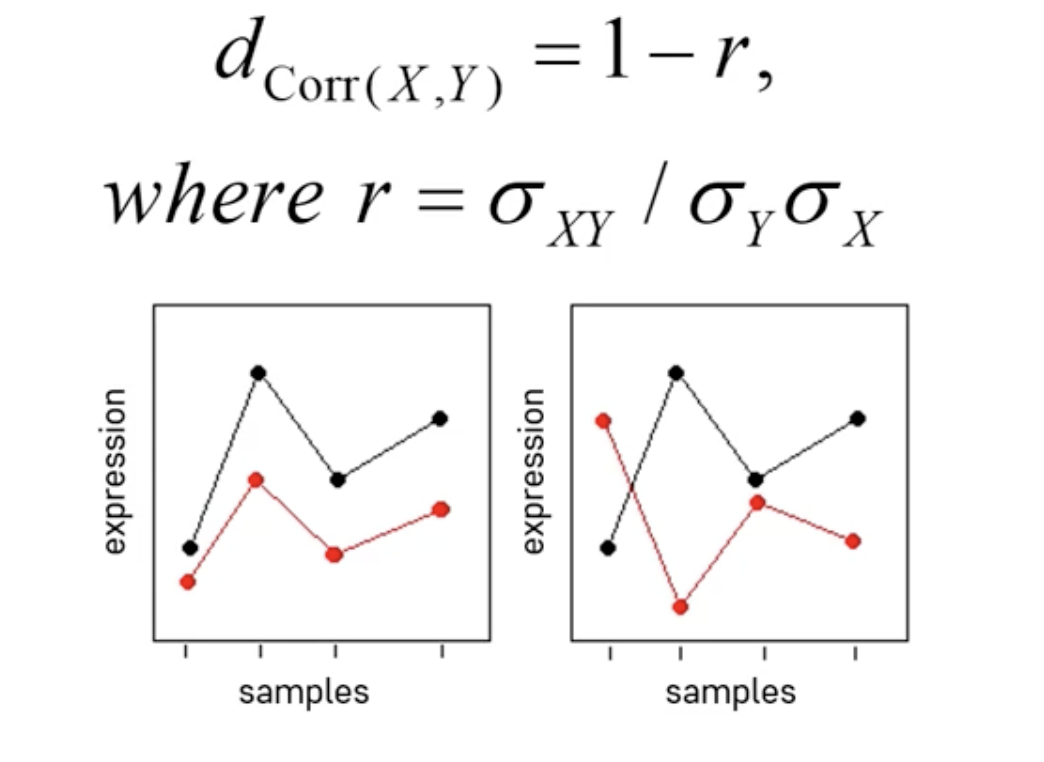
  ➡️ 관측치의 패턴 유사도를 더 많이 비교함
  ➡️ 상관계수가 크다 = 유사도가 크다
  ➡️ -1 <= r <= 1

군집화 알고리즘의 종류

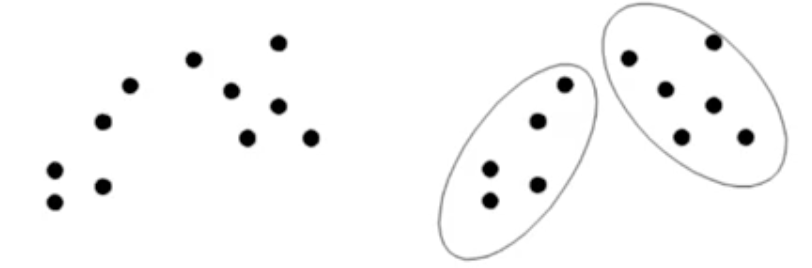
분리형 군집합

• 전체 데이터의 영역을 특정 기준에 의해 동시에 구분
• 각 개체들을 사전에 정의된 개수의 군집 중 하나에 속하게 됨
  

계층적 군집합

• 계층적 트리모형을 이용하여 개별 개체들을 유사도가 높은 순서로 통합
• 개체들을 가까운 집단부터 차근차근 묶어나가는 방식
• 군집화 결과 뿐만 아니라 유사한 개체들이 결합되는 dendrogram도 생성
  ➡️ 덴드로그램 : 개체들이 결합되는 순서를 나타내는 트리형태 구조
• 사전에 군집의 수를 정하지 않아도 수행 가능
  ➡️ 덴드로그램 생성 후 적절한 수준에서 잘라 군집 생성
  
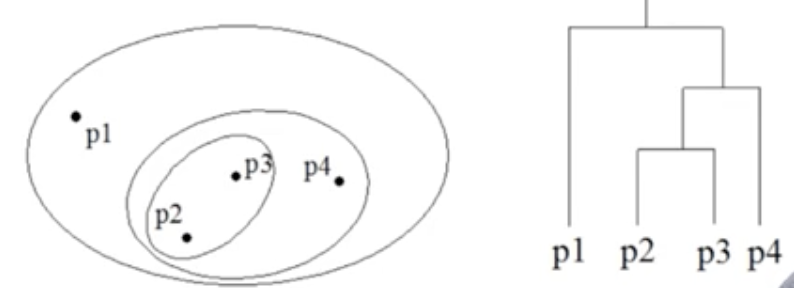
  <덴드로그램>
  

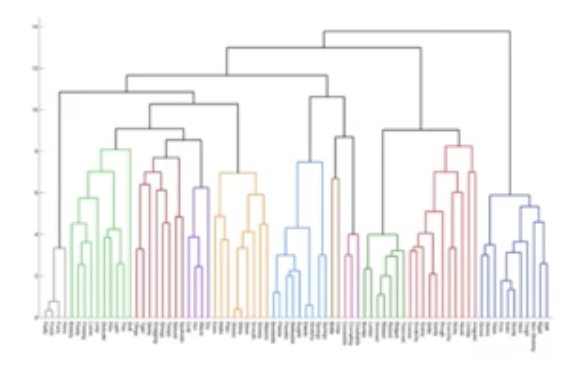
• 계층적 군집화 수행 예시
  ➡️ 모든 개체들 사이의 거리에 대한 유사도 행렬 계산
  ➡️ 거리가 인접한 관측치끼리 군집 형성
  ➡️ 유사도 행렬 업데이트
  ➡️ 위의 과정 반복

• 핵심 수행 절차 : 두 군집 사이의 유사도/거리 측정 방식
  - 단일 연결법(min), 완전연결법(max), 평균연결법(group average), etc...
  

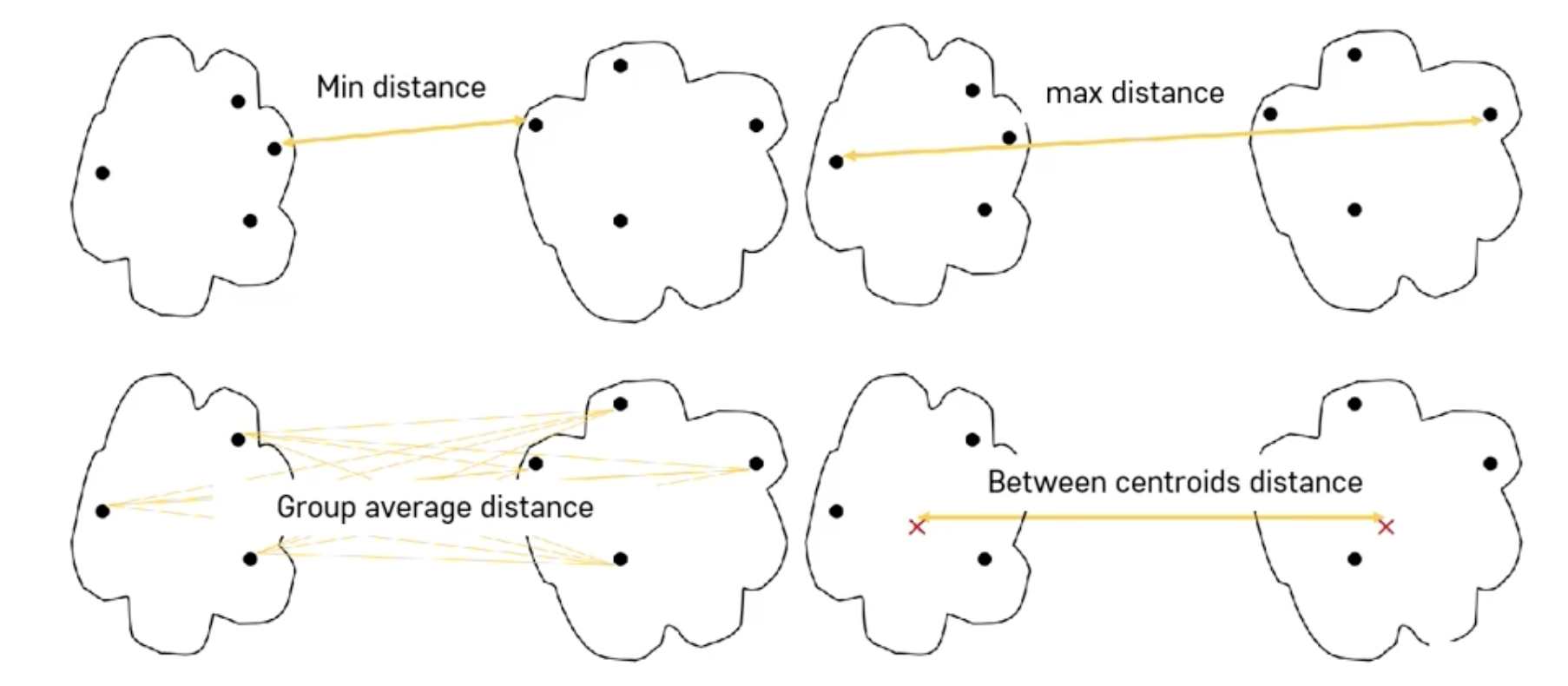
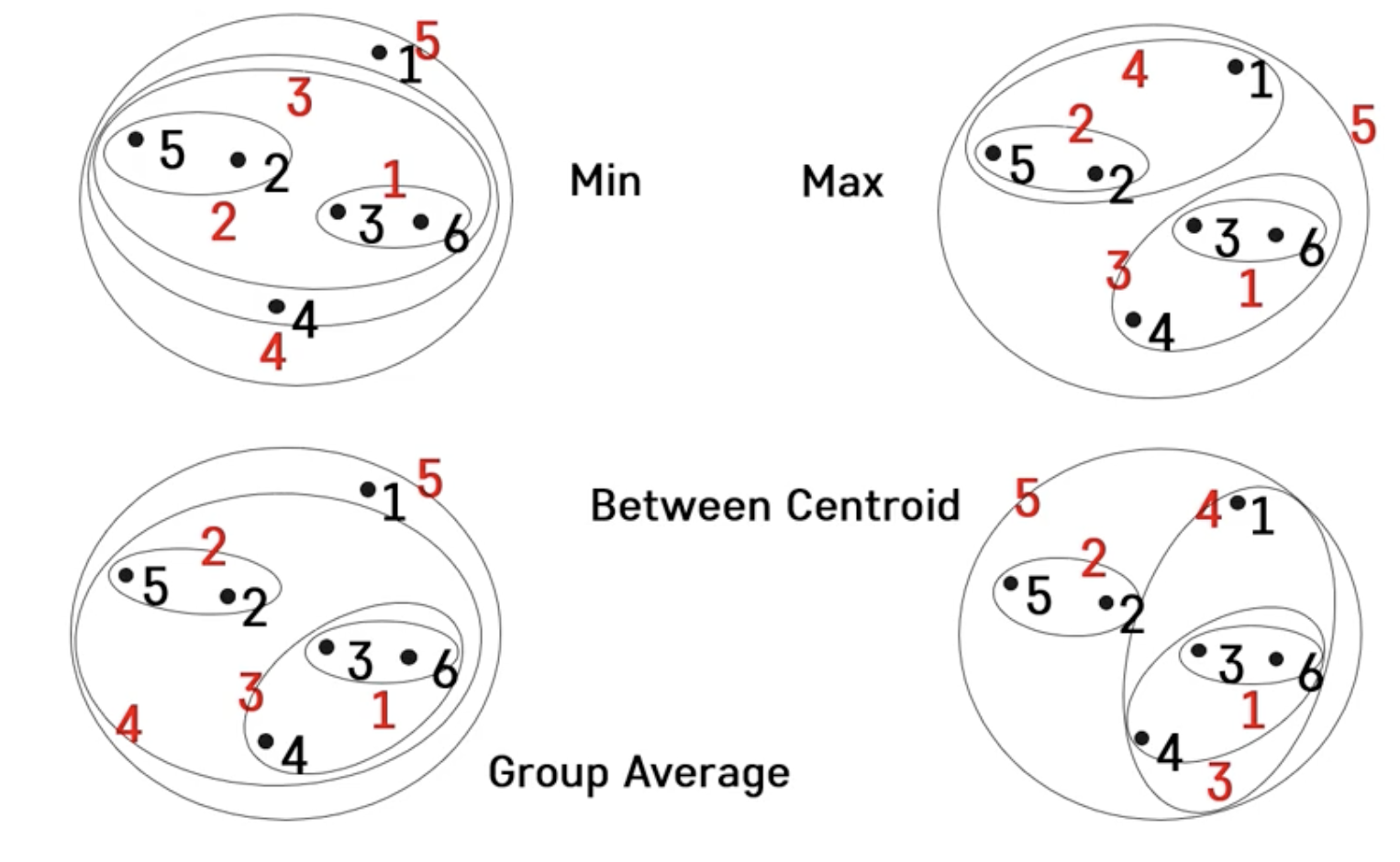
• 유사도/거리 측정 방식에 따른 군집화 결과의 차이
  

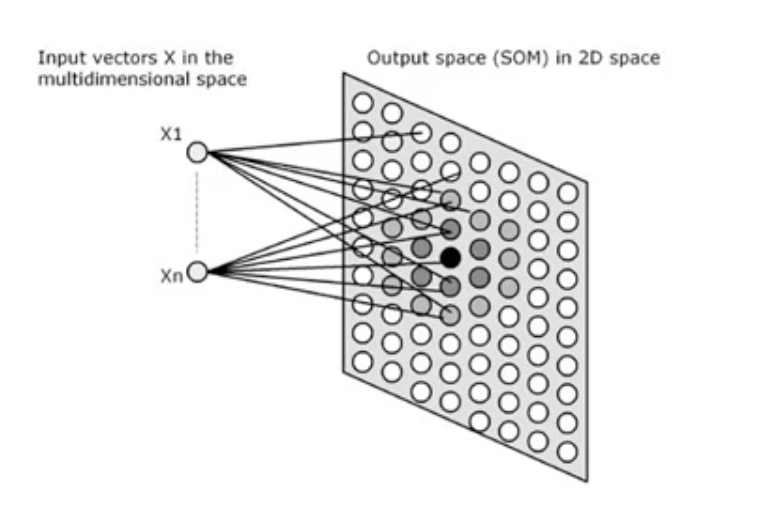
자기조직화 지도

• 2차원의 격자에 각 개체들이 대응하도록 인공신경망과 유사한 학습을 통해 군집 도출
  

분포 기반 군집화

• 데이터의 분포를 기반으로 높은 밀도를 갖는 세부 영역들로 전체 영역을 구분
  

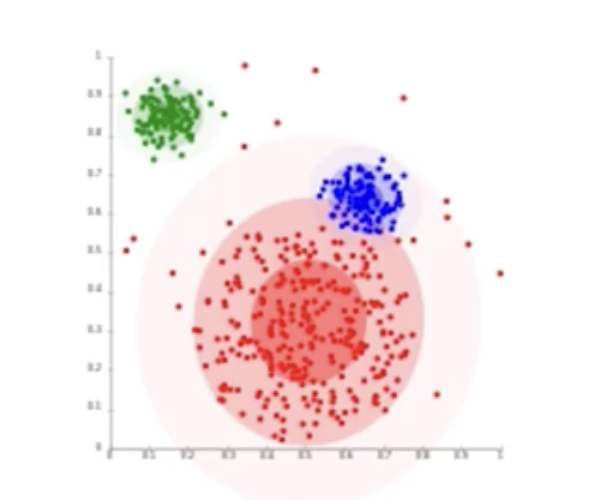
K-means Clustering

K-평균 군집화

• 대표적인 분리형 군집화 알고리즘
• 각 군집은 하나의 중심(centroid)를 가짐
• 각 개체는 가장 가까운 중심에 할당하는 것이 원칙
• 같은 중심에 할당된 개체들이 모여 하나의 군집을 형성
• 사전에 군집의 수 K를 정해줘야 함 (Hyperparameter)
  

K-평균 군집화 수행 절차

1. 초기 중심(centroid)를 k개 임의로 생성
2. 개별 관측치로부터 각 중심까지의 거리를 계산 후, 가장 가까운 중심이 이루는 군집에 관측치 할당
3. 각 군집의 중심을 다시 계산
4. 중심이 변하지 않을 때까지 위 2, 3의 과정을 반복
   ➡️ 초기 중심은 무작위로 생성하기 때문에 군집화 결과가 초기 중심 설정에 따라 다르게 나타나는 경우가 발생할 수도 있음

k-평균 군집화 수행 예시 (k=2)

1. 2개의 중심을 임의로 생성
2. 생성된 중심들을 기준으로 모든 관측치에 군집을 할당
3. 각 군집의 중심을 다시 계산
4. 중심이 변하지 않을 때까지 위의 과정 반복
   

초기 중심 설정이 최종 결좌에 어떤 영향을 미치는가?

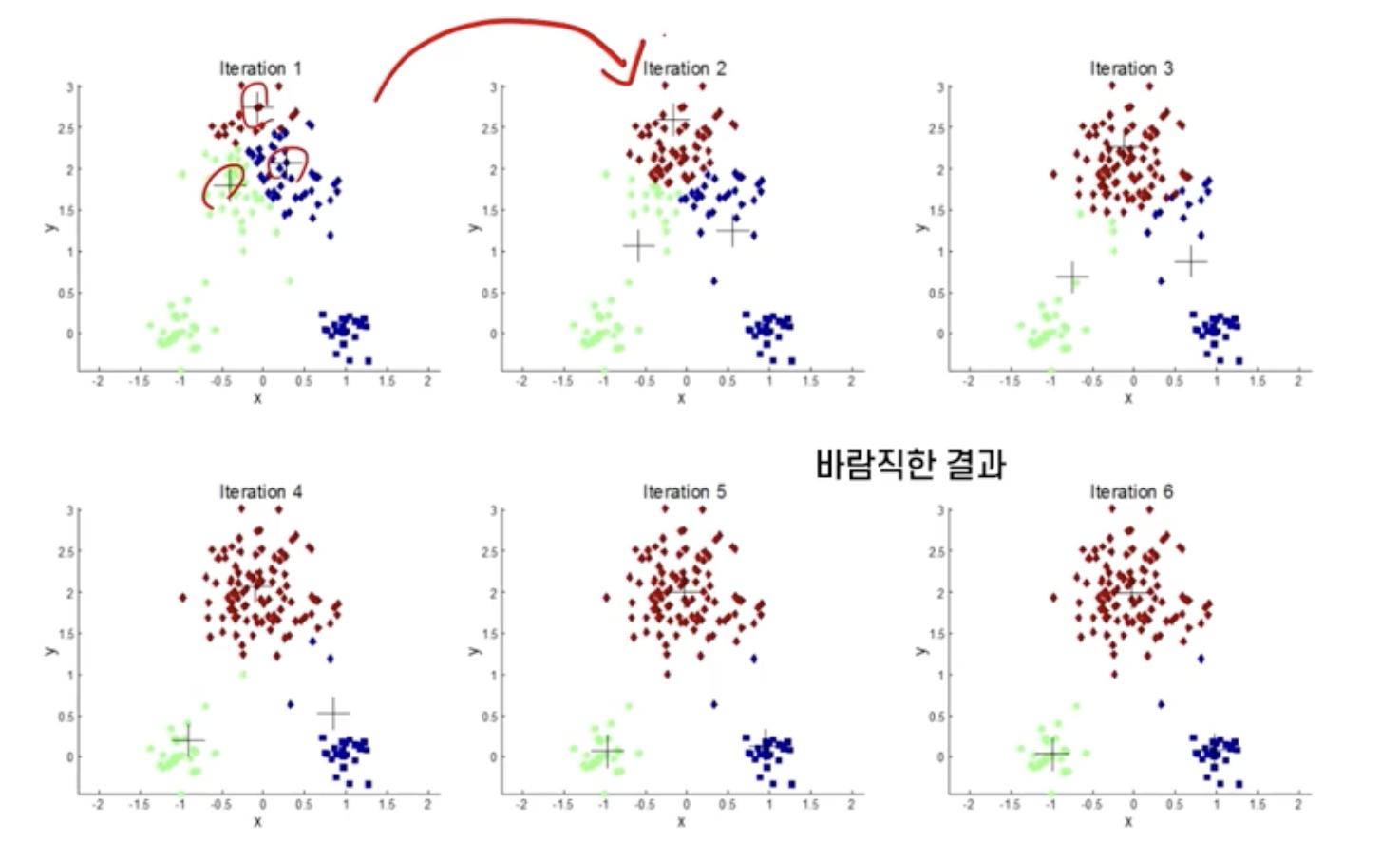
무작위 초기 중심 설정의 위험을 피하고자 많은 연구 존재

• 반복 수행으로 가장 여러 번 나타나는 군집을 사용
• 일부 데이터만을 샘플링하여 계층적 군집화 수행 후 초기 군집 중심 설정
• 데이터 분포 정보를 사용하여 초기 중심 설정
• 하지만 많은 경우 초기 중심 설정이 최정 결과에 큰 영향을 주진 않음

k-평균 군집화의 문제점

1. 서로 다른 크기의 군집을 잘 찾아내지 못함
   

2. 서로 다른 밀도의 군집을 잘 찾아내지 못함
   

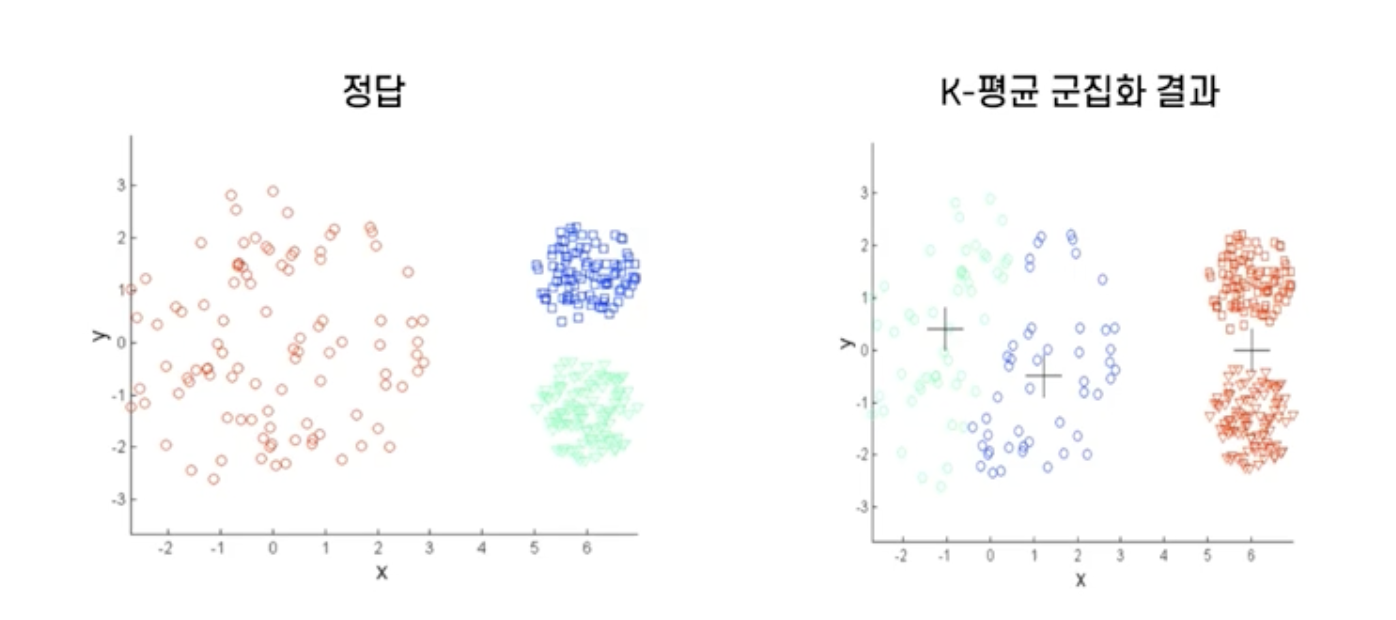
3. 지역적 패턴이 존재하는 군집을 판별하기 어려움
   

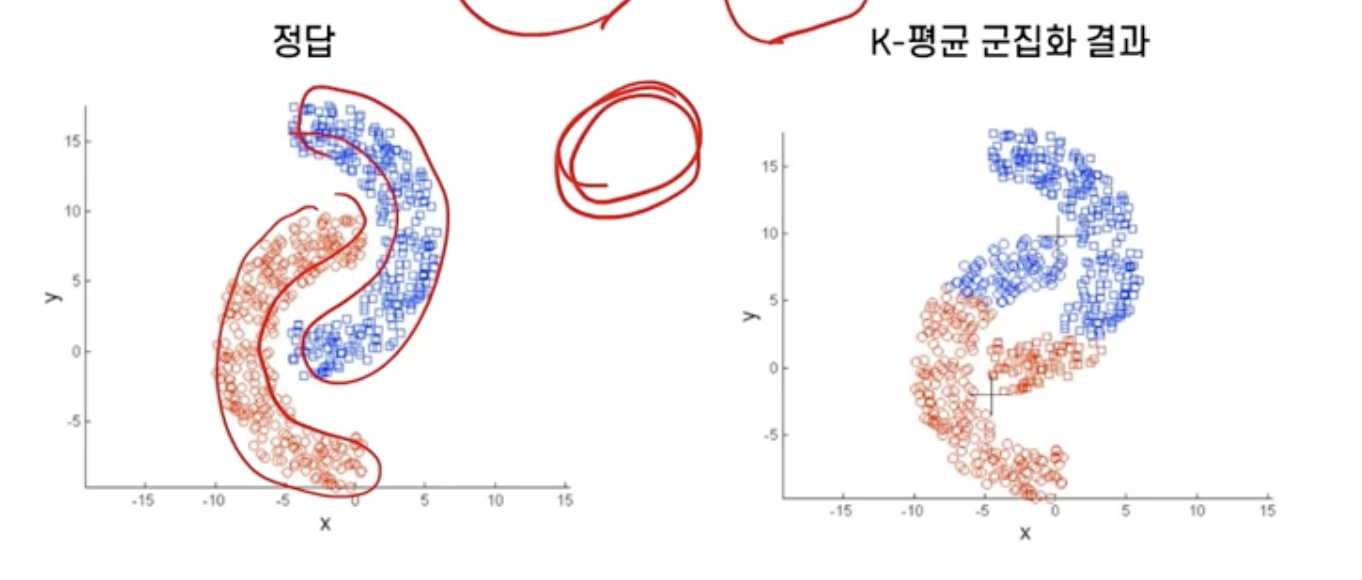
군집화 결과 측정 및 평가

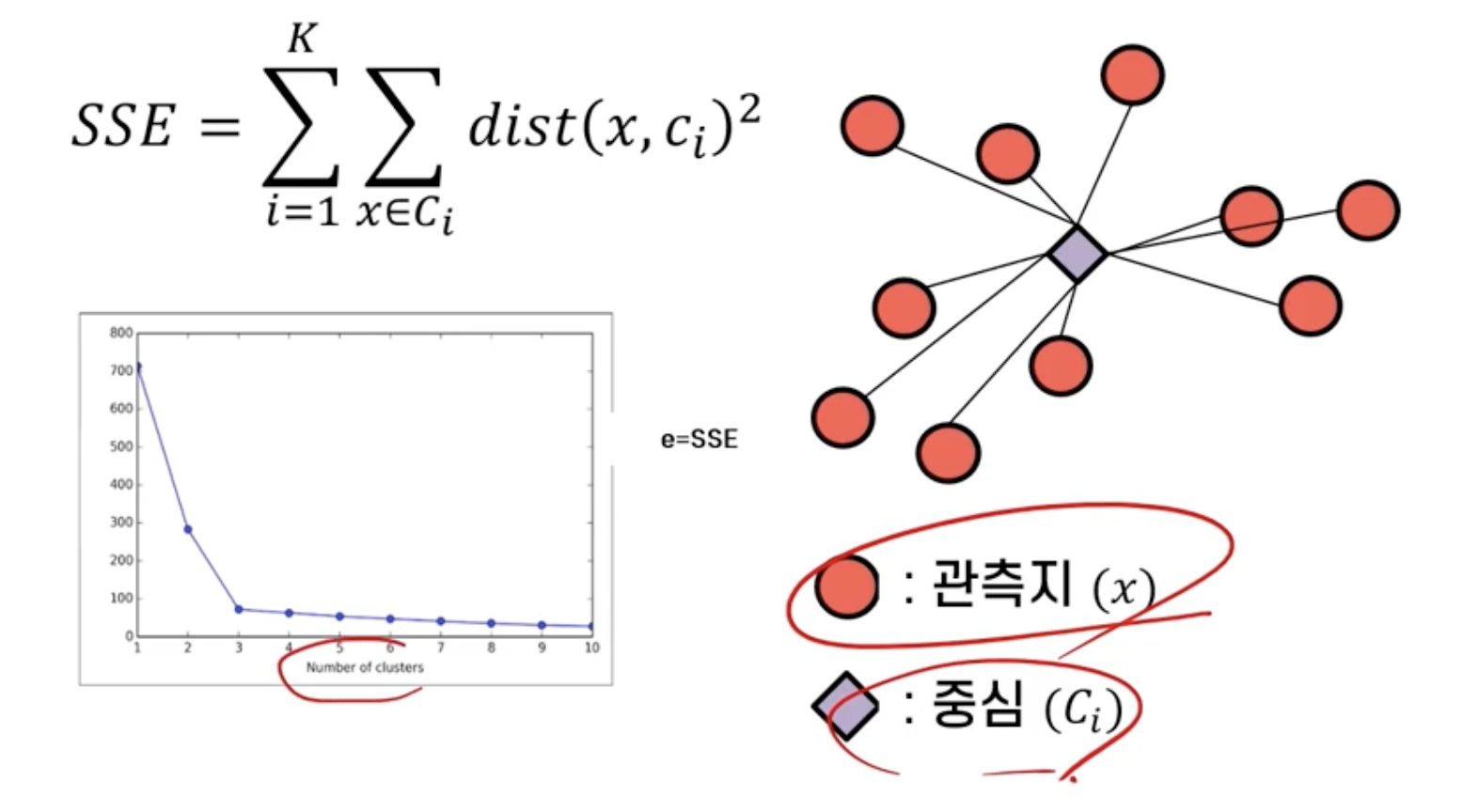
최적의 군집 수 결정

➡️ 다양한 군집 수에 대해 성능 평가 지표를 도시하여 최적의 군집 수 선택
➡️ Elbow point에서 최적 군집 수가 결정되는 경우가 일반적

군집화 평가 지표

1. Sum of Squared Error (SSE)

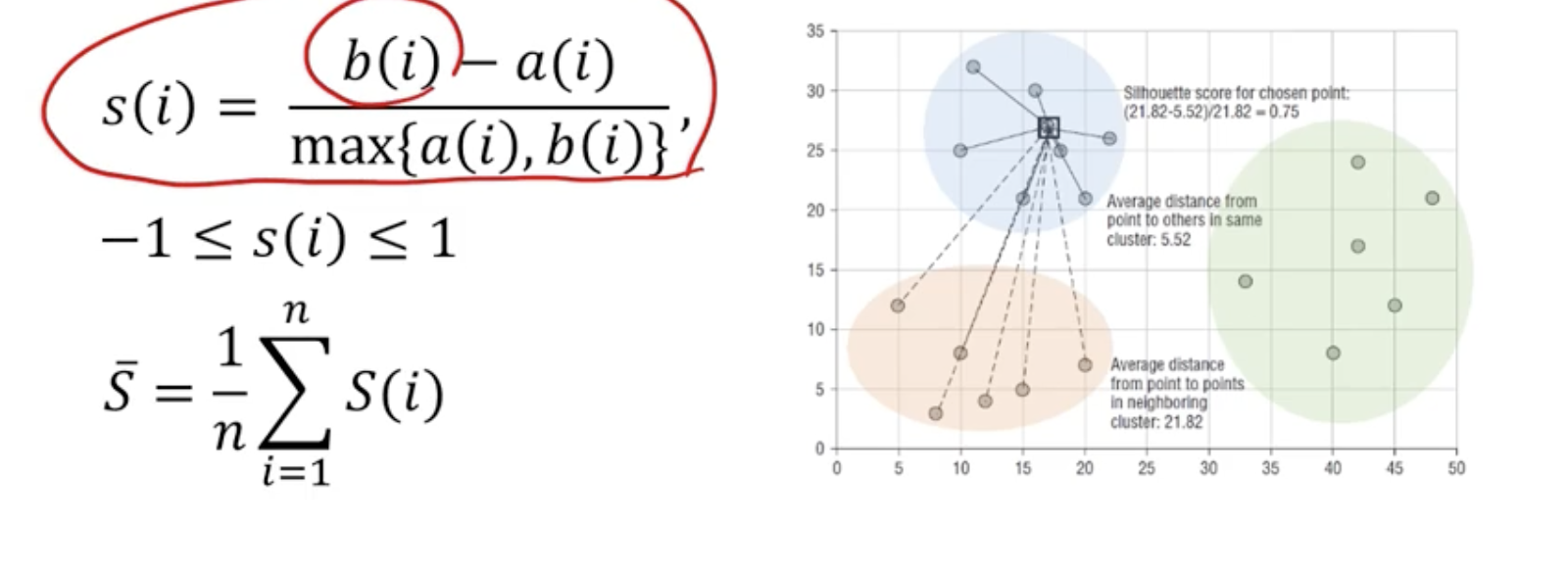
2. Silhouette

• a(i): 관측치 i로부터 같은 군집 내에 있는 모든 다른 개체들 사이의 평균 거리 (내부)
• b(i): 관측치 i로부터 다른 군집 내에 있는 개체들 사이의 평균 거리 중 최솟값 (외부)

➡️ 일반적으로 S의 값 0.5보다 크면 군집 결과가 타당하다고 볼 수 있음

reference : K-MOOC 실습으로 배우는 머신러닝