- 자료에 중복된 정보가 많을 경우, 자료가 갖는 차원보다 더 작은 수의 차원으로도 자료에 내재한 정보를 설명할 수 있을 것
주성분분석(PCA)
: 처음 몇몇개의 차원이 정보를 최대한 많이 설명할 수 있도록 자료를 새로운 방향에서 바라보도록 하는 방법
- 한 각각의 성분은 다른 성분과는 상관이 없고, 이는 이후 회귀분석과 같은 종속관계 분석을 할 때 다중공선성(Multicollinearity)을 없애는 이점을 줌

런닝머신과 수영 점수 예제
런닝머신과 수영 점수간의 상관관계
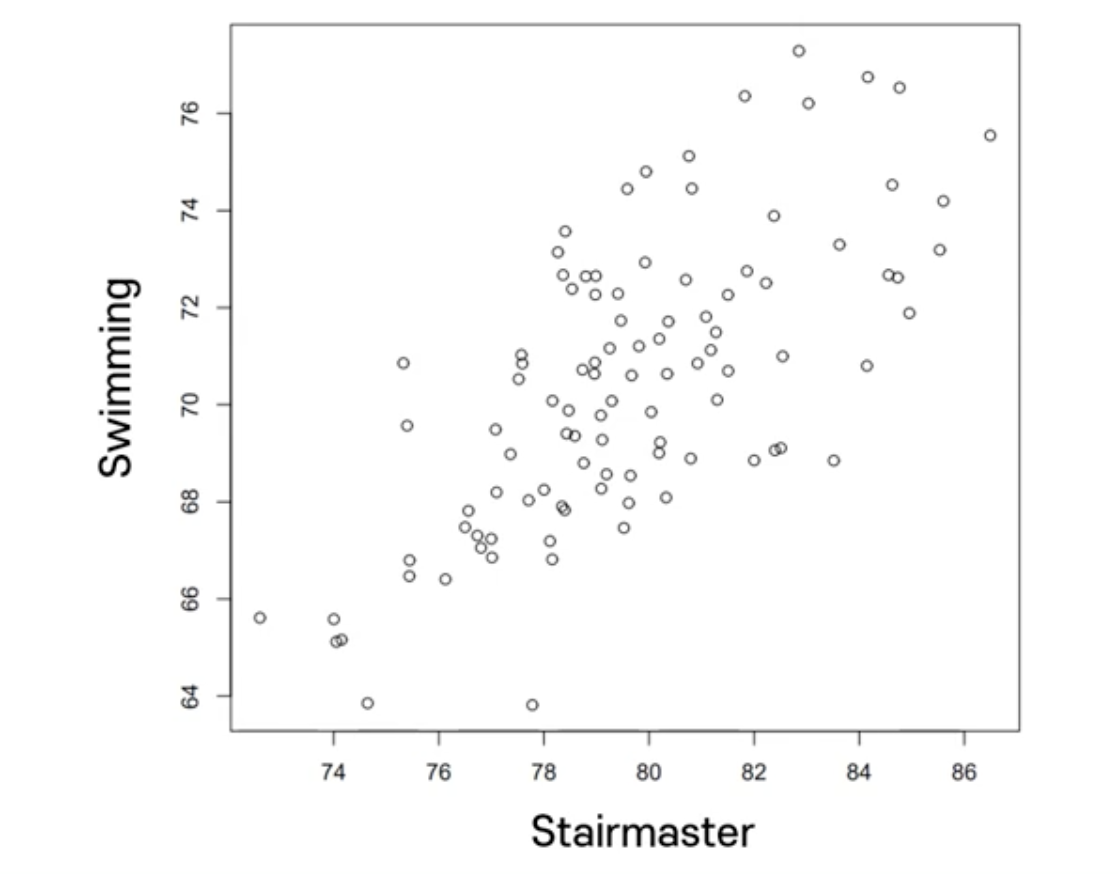
➡️ 런닝 머신을 잘 할수록 수영도 잘 한다.
➡️ 둘 다 동일한 정보를 내포하고 있다면 하나의 정보만 사용 가능
- 위의 산점도를 보면 하나의 차원 (체력)이 수영 점수와 런닝머신 점수에 내재하는 정보의 대부분을 갖고 있음을 알 수 있음
- 즉, 분산을 크게 하는 수영점수와 런닝머신 점수의 선형결합을 첫 주요한 성분으로 얻을 수 있음
- 선형결합은 2차원의 공간에 있는 점들을 하나의 축 상으로 투영한다는 것을 의미함
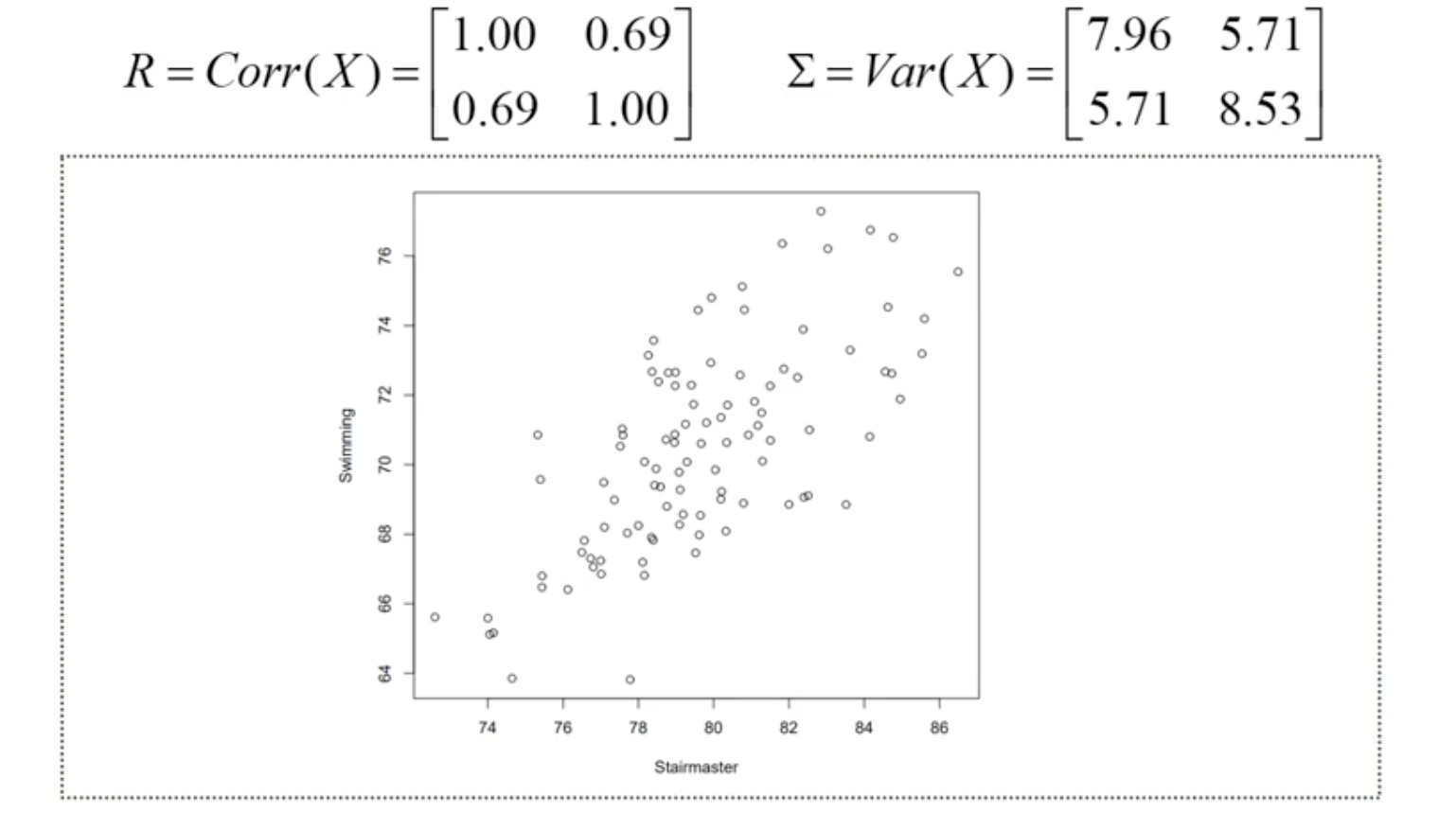
X1(런닝머신)과 X2(수영) 점수의 상관계수와 공분산행렬
비타민 예제
- 196명을 대상으로 한 설문결과로부터 상관계수를 구하면 다음과 같음
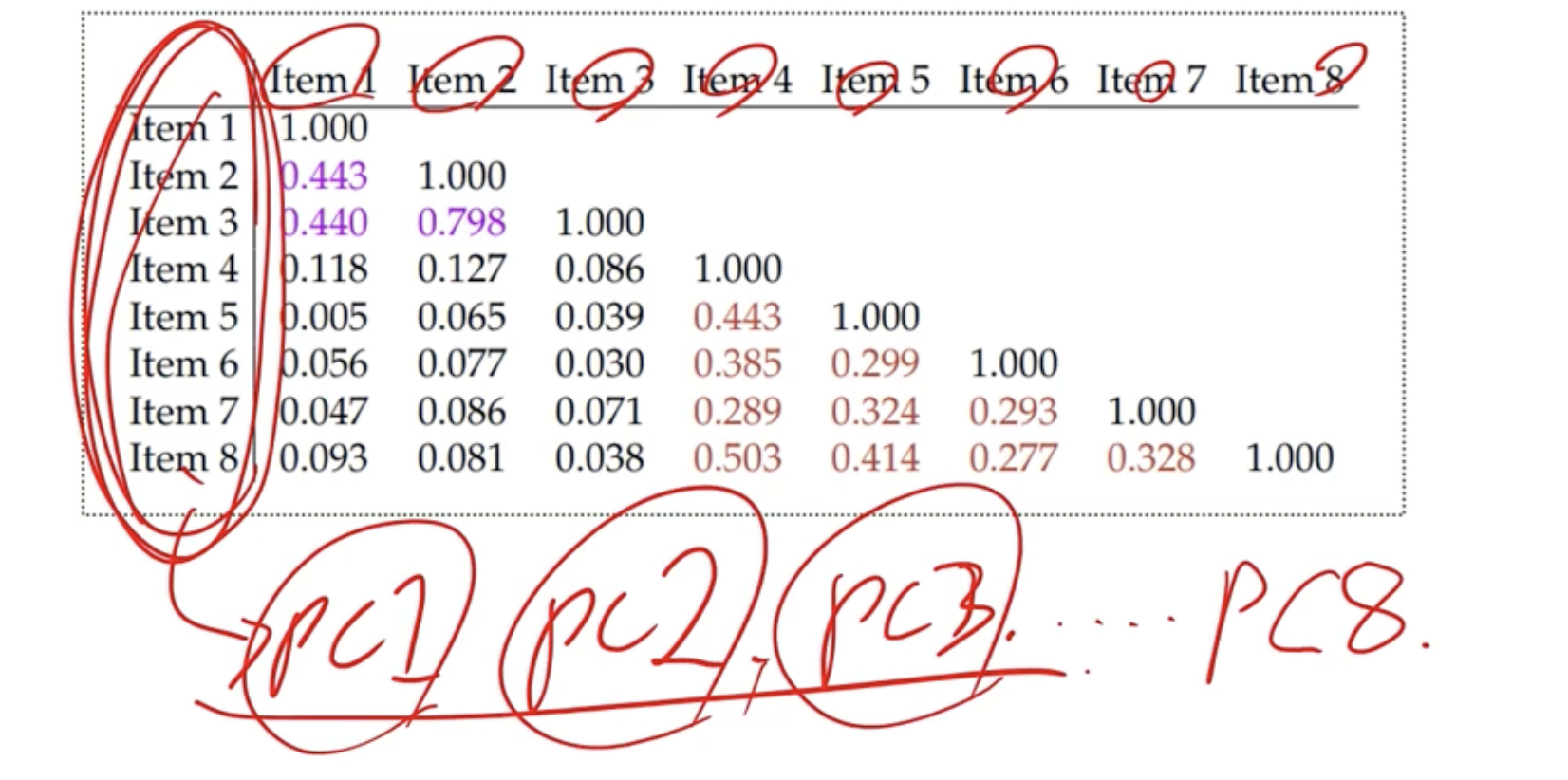
➡️ 8개의 문항과 관련한 정보를 더 간단한 것으로 요약하는 데 관심이 있음
PCA 적용
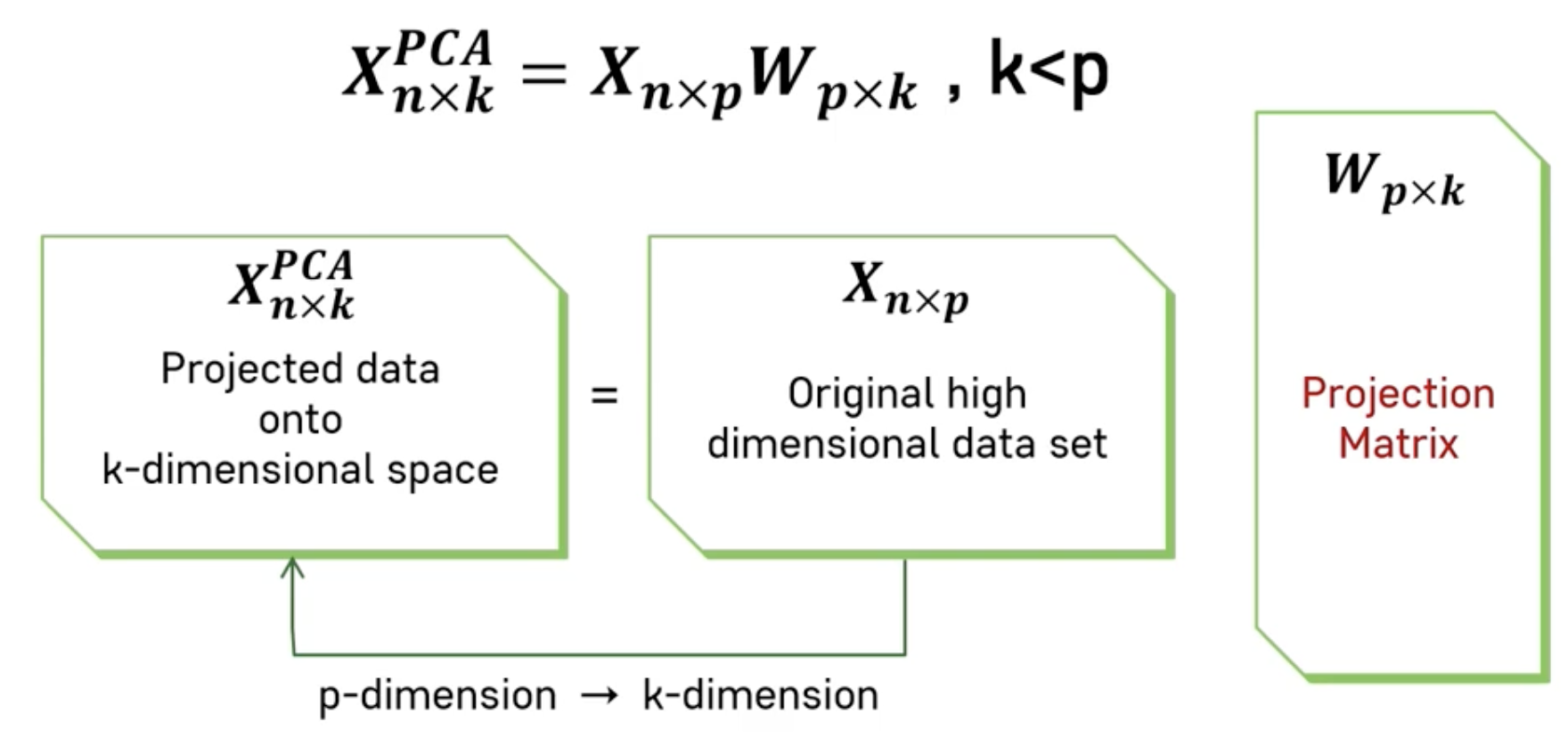
- 고차원 데이터의 차원축소 원리
- 선형변환 행렬 이용
1) 데이터 정규화
➡️ 각 변수 값들의 평균 = 0

2) 최적화 문제 정의
- 데이터 X를 새로운 축에 사영시킨 Z의 분산을 최대화하는 W를 찾는 것이 목표

3) 최적해 도출
- Lagrangian multiplier 사용해서 제약식을 목적식에 추가한 새 목적식 생성
- 새 목적식을 미분하여 기울기가 0이 되는 점에서 최적해 발생
4) 고유벡터(eigenvector)들을 고유값(eigenvalue) 기준으로 내림차순 정렬
- 각 고유벡터는 선형변환된 공간에서 서로 직교하는 새로운 축이 됨

5) 변수추출을 통한 데이터 변환
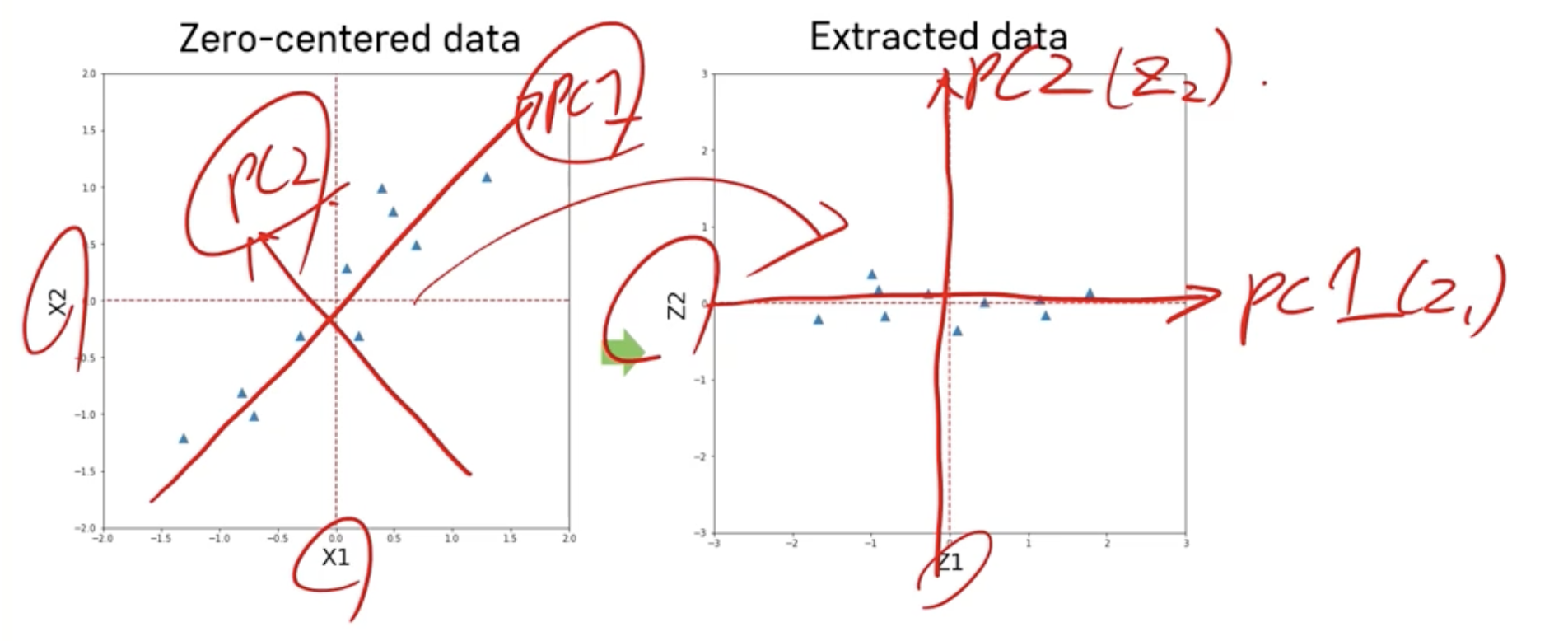
6) 추출된 변수 중 일부만을 사용하여 데이터 역변환
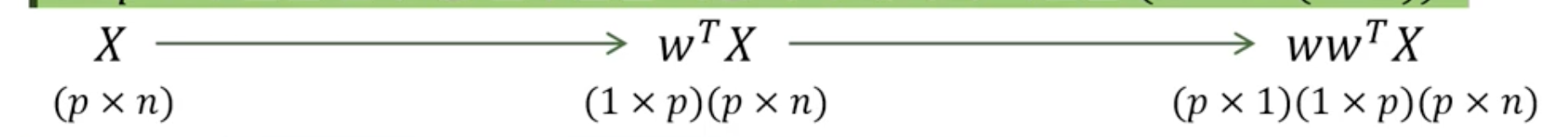
Scree Plot
: 최적의 주성분 개수를 정할 때 사용
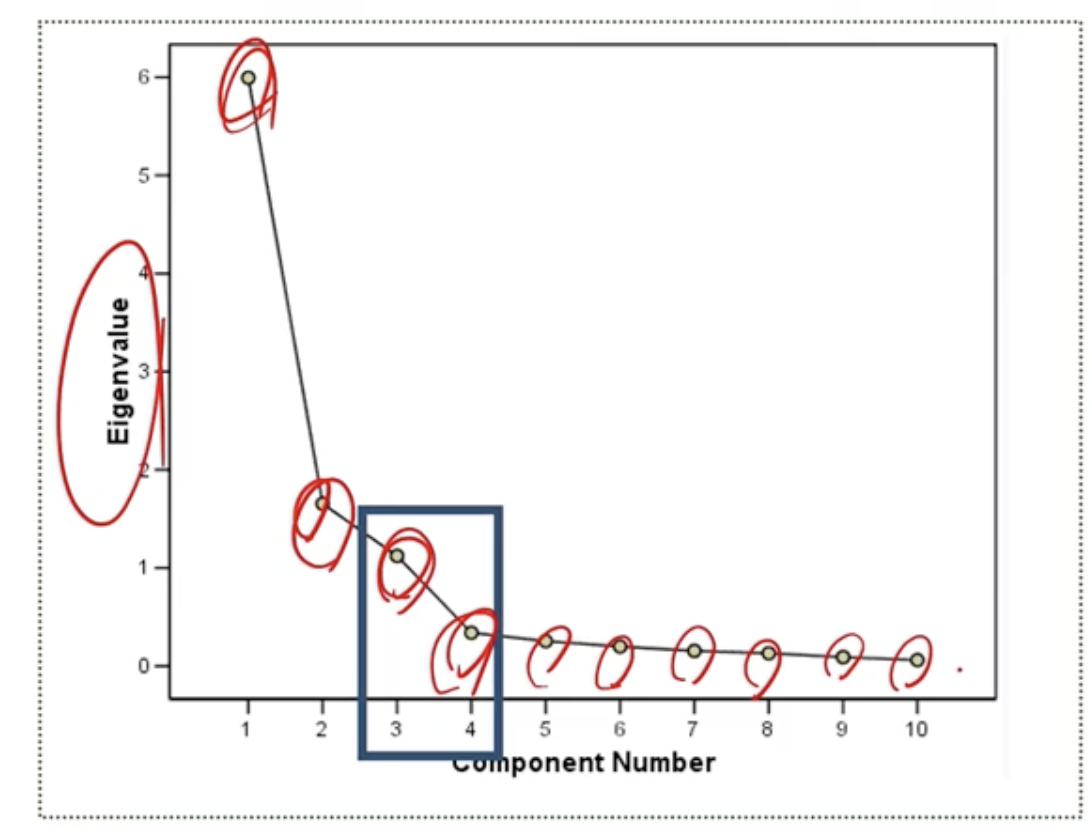
➡️ Elbow 포인트 찾기
Loading Plot
: 각 주성분을 만들 때, 기존 데이터 X의 각 변수가 기여하는 정도를 판단

reference : K-MOOC 실습으로 배우는 머신러닝
