기계학습
- A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P
기계학습 유형
- Supervised Learning
- Unsupervised Learning
- Reinforcement Learning
Supervised Learning
- 출력 변수가 연속형 ➡️ Regression
- 출력 변수가 범주형 ➡️ Classification
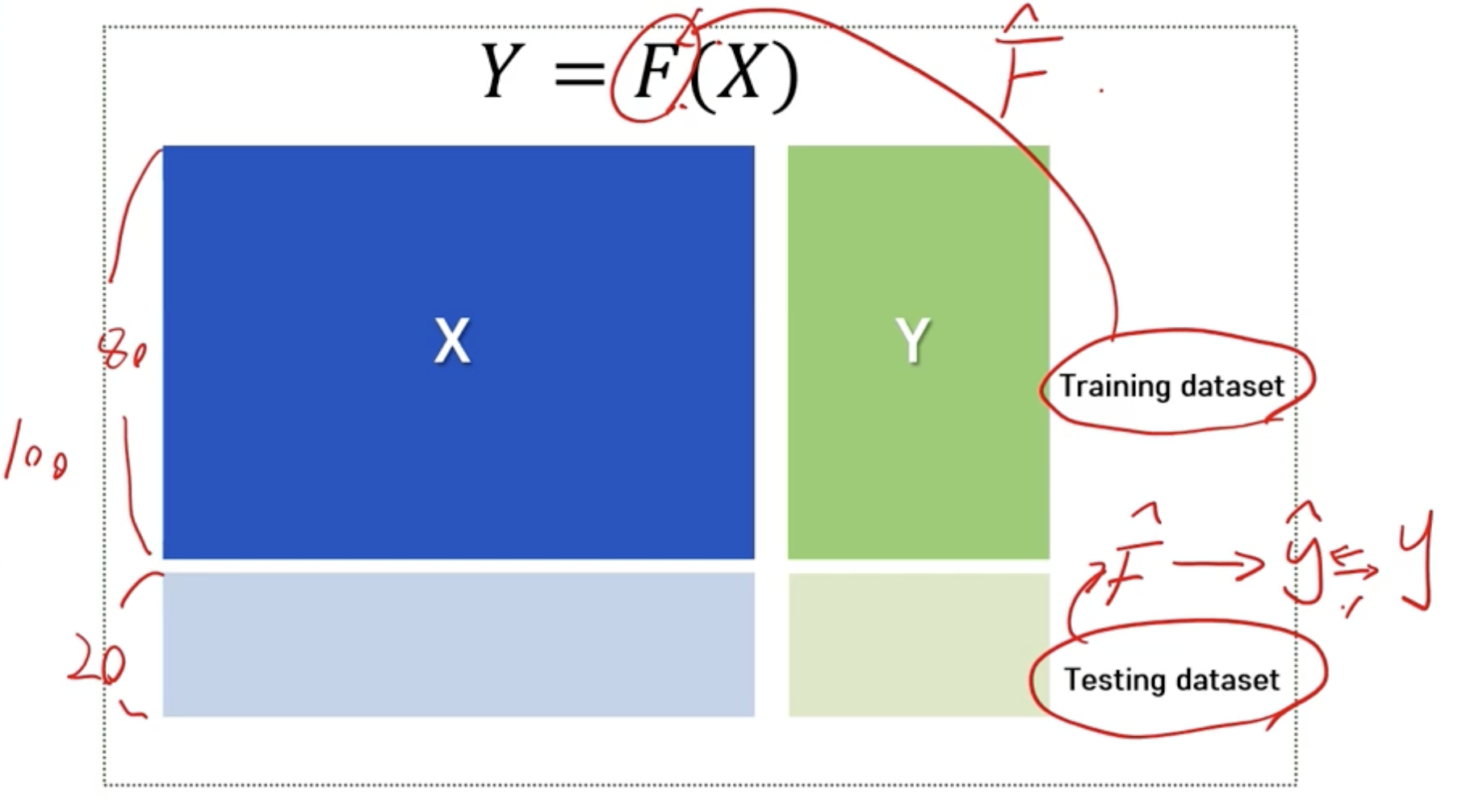
- Training 데이터와 Testing 데이터로 나누어 평가
Bias-Variance Tradeoff
- 모든 모델은 복잡도를 통제할 수 있는 Hyperparameter를 갖고 있음
- 가장 좋은 성능을 낼 수 있는 모델을 학습하기 위해 최적의 Hyperparameter를 결정해야 함
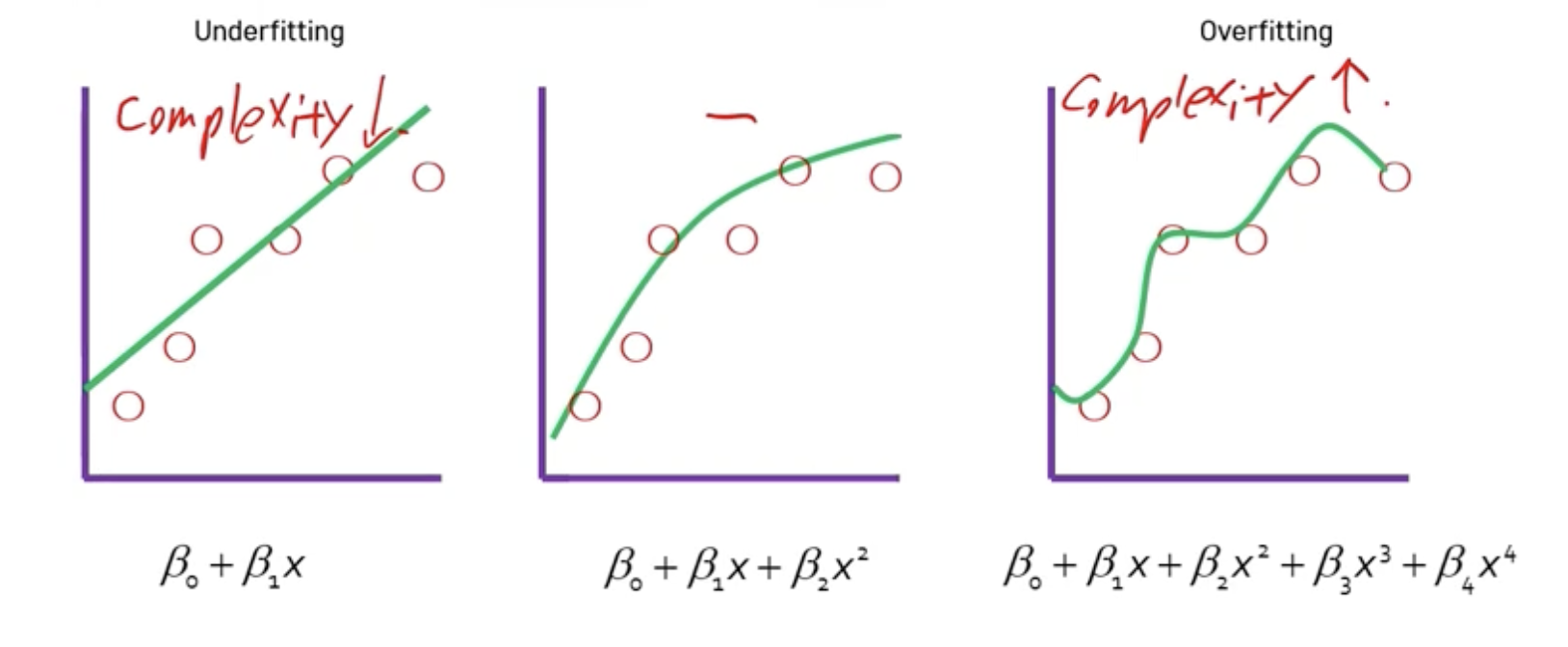
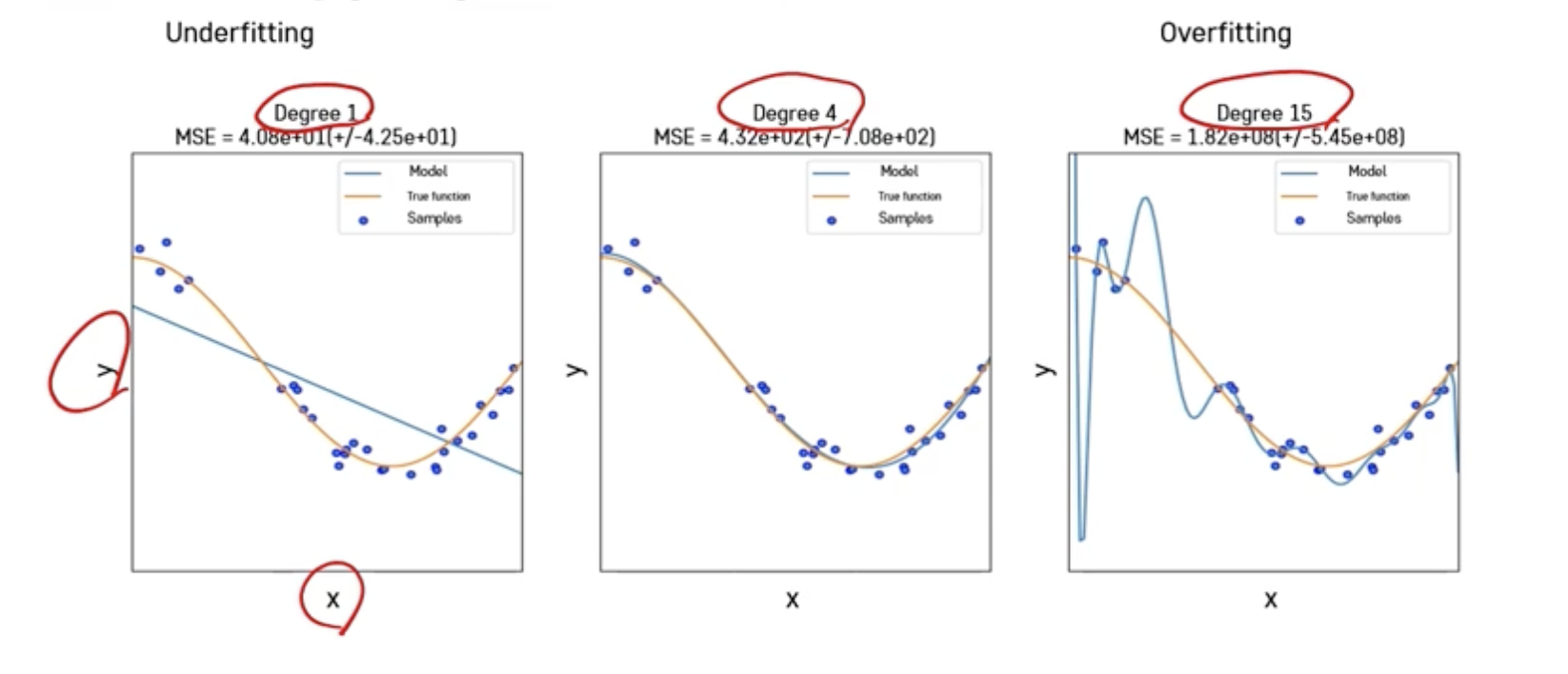
➡️ underfitting, overfitting 둘 다 성능 안좋음
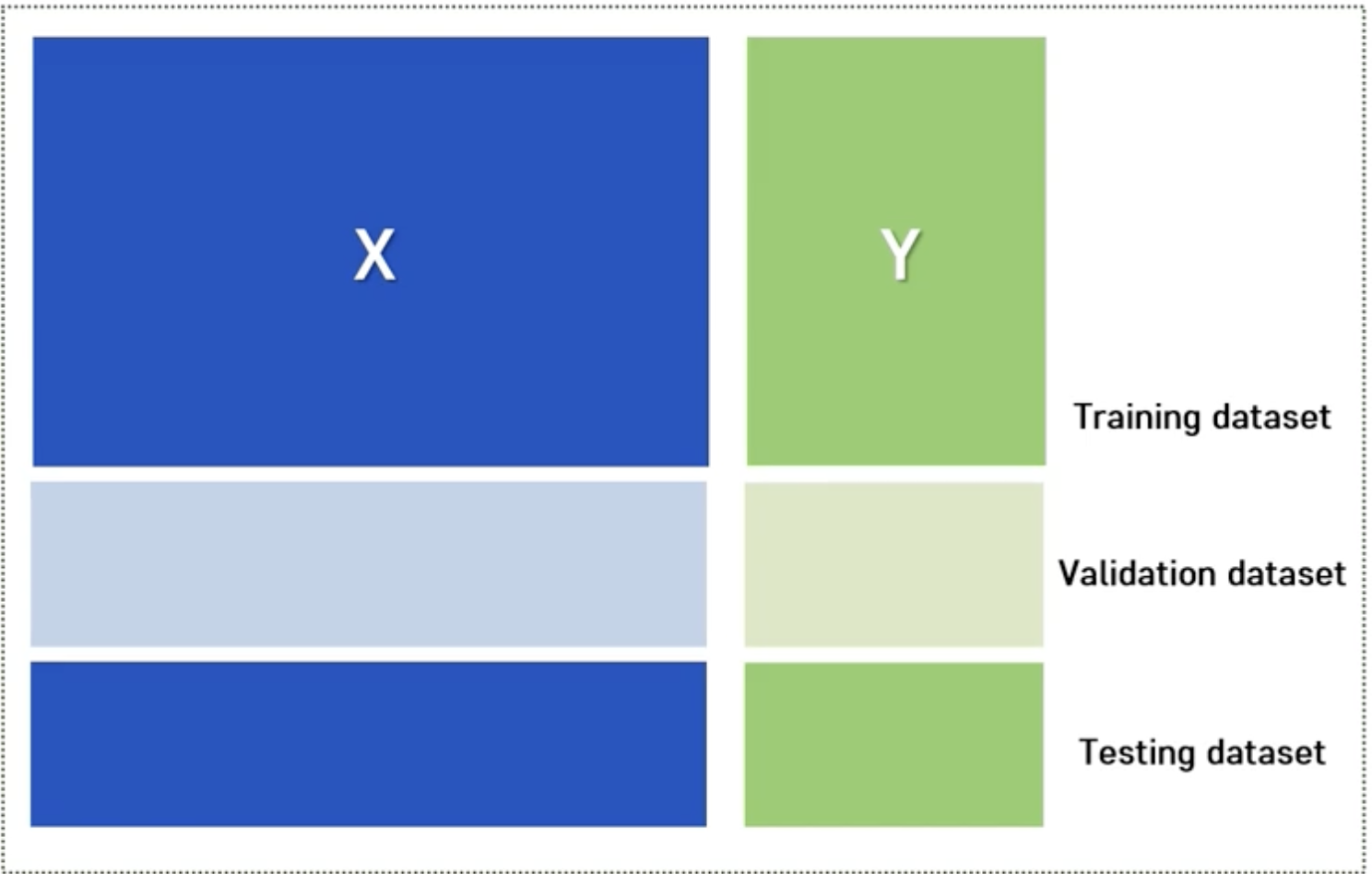
Validation Set
- 좋은 모델을 선택하기 위한 검증 데이터 셋
Classification 예시
- 범주형 (Categorical) 종속 변수 : Class, Label
- 분류 문제의 예시
- 제품이 불량인지 양품인지 분류
- 고객이 이탈고객인지 잔류고객인지 분류
- 카드 거래가 정상적인 사기인지 분류(Fraud Detection) - 특정 모델이 모든 경우에 대해 항상 좋은 성능을 낸다고 보장할 수 없음
- 문제 상황에 따라 적합한 모델을 선택해야 함
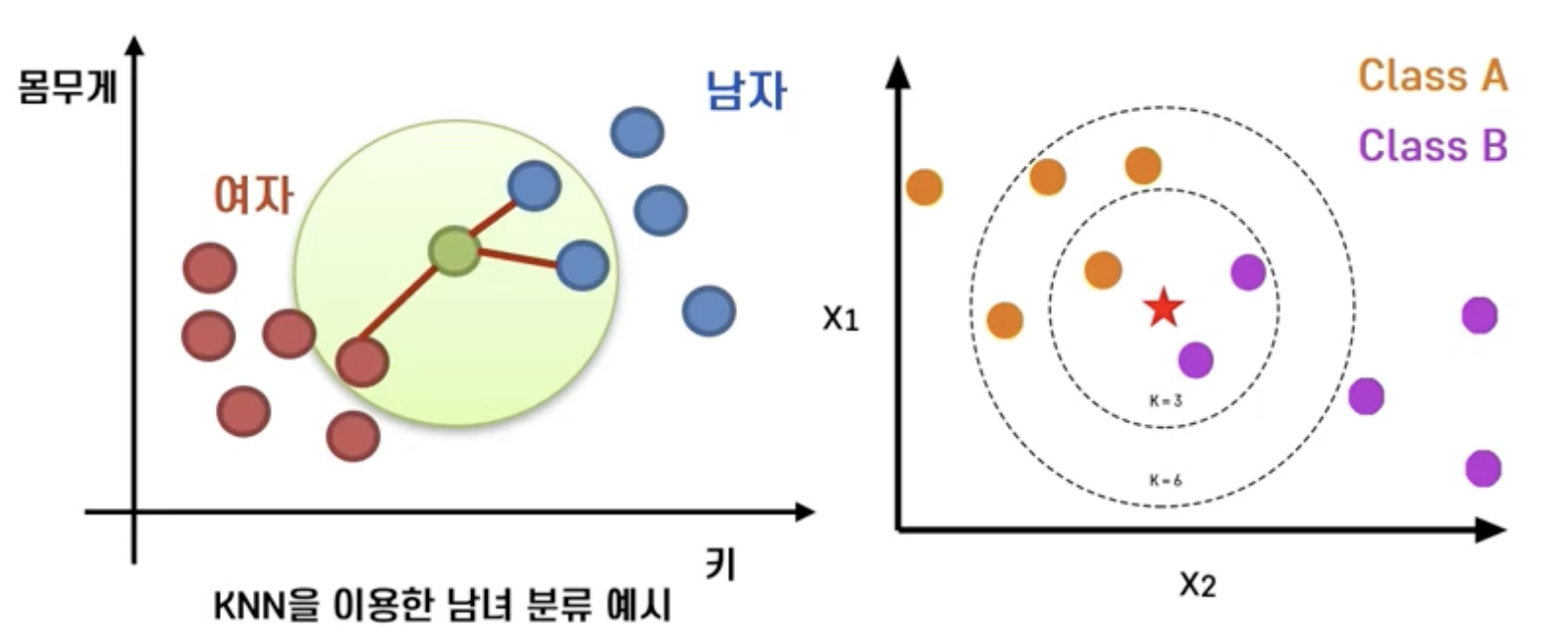
KNN (K-Nearest Neighbors)
- '두 관측치의 거리가 가까우면 Y도 비슷하다'
- K개의 주변 관측치의 Class에 대한 majority voting
- Distance-based model, instance-based learning
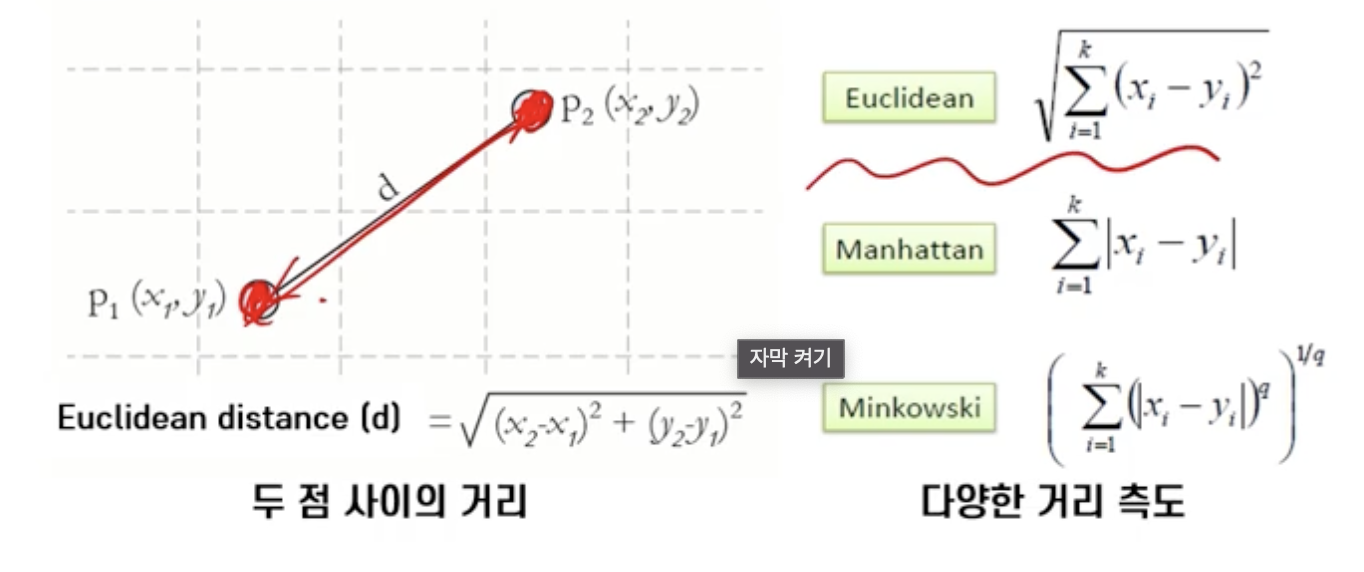
거리
- 두 관측치 사이의 거리를 측정할 수 있는 방법
- 범주형 변수는 Dummy Variable 으로 변환하여 거리 계산
K의 영향
- K : KNN의 Hyperparameter
- K가 클수록 Underfitting
- K가 작을수록 Overfitting
- Validation dataset을 이용해 최적의 K 결정

Logistic Regression
다중선형회귀분석
- 목적 : 수치형 설명변수 X와 종속변수 Y간의 관계를 선형으로 가정하고 이를 가장 잘 표현할 수 있는 회귀 계수를 추정
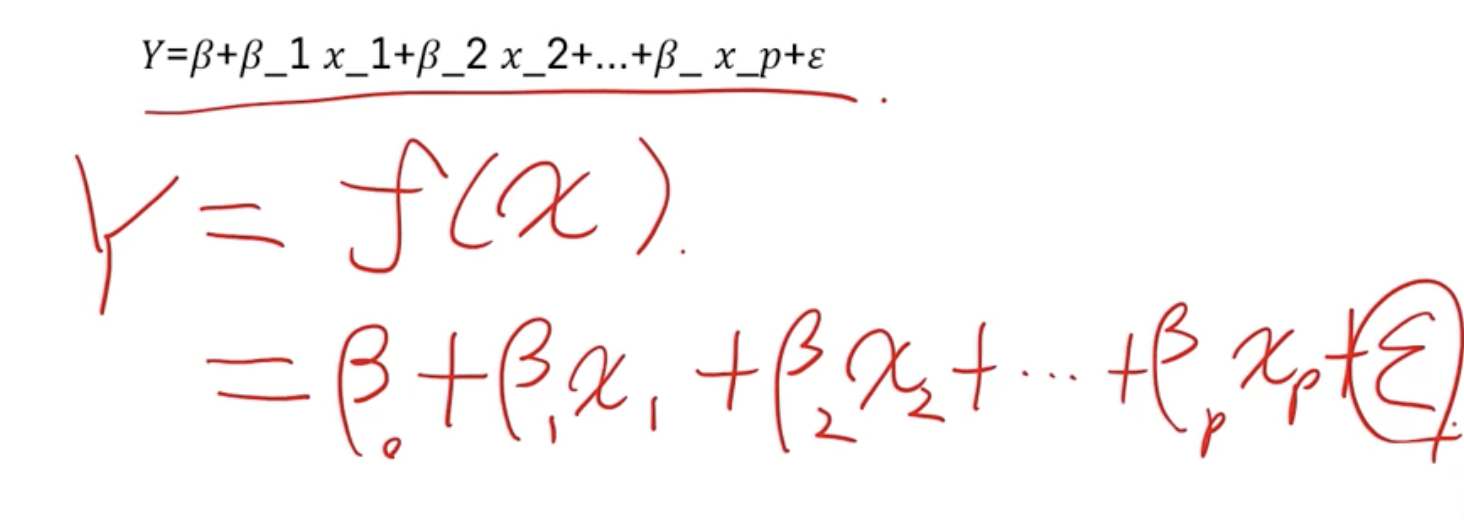
- Loss = MSE
- Minimize loss
Logistic Regression의 필요성
-
종속 변수의 속성이 이진 변수일 때 (0 or 1)
Q) 확률값을 선형 회귀분석의 종속변수로 사용하는 것이 타당한가?
A) 선형회귀분석의 우변은 범위에 대한 제한이 없기 때문에 우변과 좌변의 범위가 다른 문제점이 발생 -
로지스틱 회귀분석의 목적
: 이진형의 형태를 갖는 종속변수(분류문제)에 대해 회귀식의 형태로 모형을 추정하는 것 -
왜 회귀식으로 표현해야 하는가?
: 회귀식으로 표현될 경우 변수의 통계적 유의성 분석 및 종속변수에 미치는 영향력 등을 알아볼 수 있음 -
로지스틱 회귀분석의 특징
- 이진형 종속변수 y를 그대로 사용하는 것이 아니라 y에 대한 로짓함수(logit function)를 회귀식의 종속변수로 사용
- 로짓함수는 설명변수의 선형결합으로 표현됨
- 로짓함수의 값은 종속변수에 대한 성공확률로 역산될 수 있으며 따라서 이는 분류 문제에 적용 가능함
시그모이드 함수

Cross-Entropy
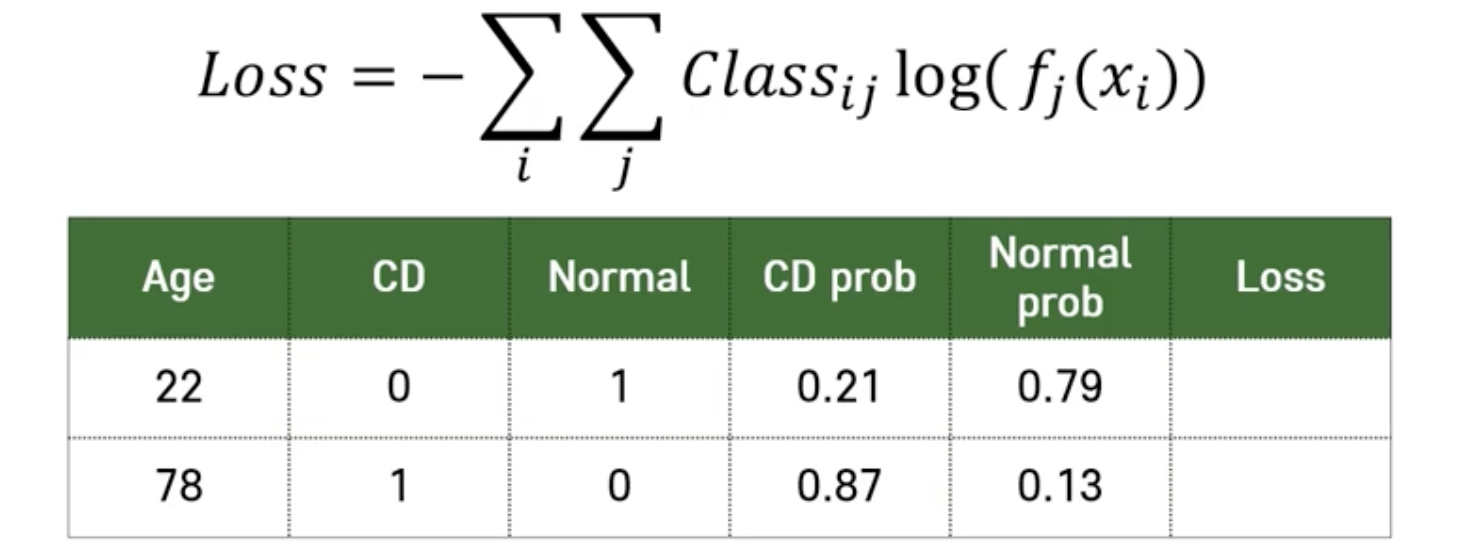
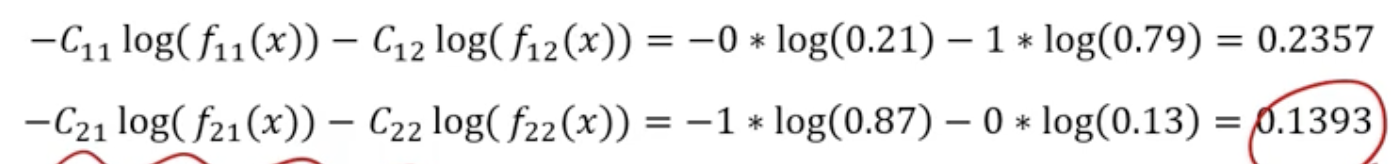
➡️ Minimizing loss corresponds to maximize the probability of classifying to correct class!
reference : K-MOOC 실습으로 배우는 머신러닝
