1. 분포 (Distribution)

1) 왜도

• 일변량 양적 자료가 대칭인지 아닌지 알려주는 정보
• 왜도 값이 0에 가까울수록 대칭이라고 봄

2) 첨도

• 일변량 양적 자료의 중심이 얼마나 뾰족한지 알려주는 정보
• 첨도 값이 클수록 중심이 뾰족해짐

2. 정규분포 (Normal Distribution)

1) 특징

• 기호 : X ~ N(μ,σ^2)
• 모평균(μ)을 기준으로 모표준편차(σ)에 의해 종 모양으로 생긴 좌우대칭의 분포
• 정규분포일 때만 성립
• σ 에 따른 정규분포의 면적은 아래와 같음
  
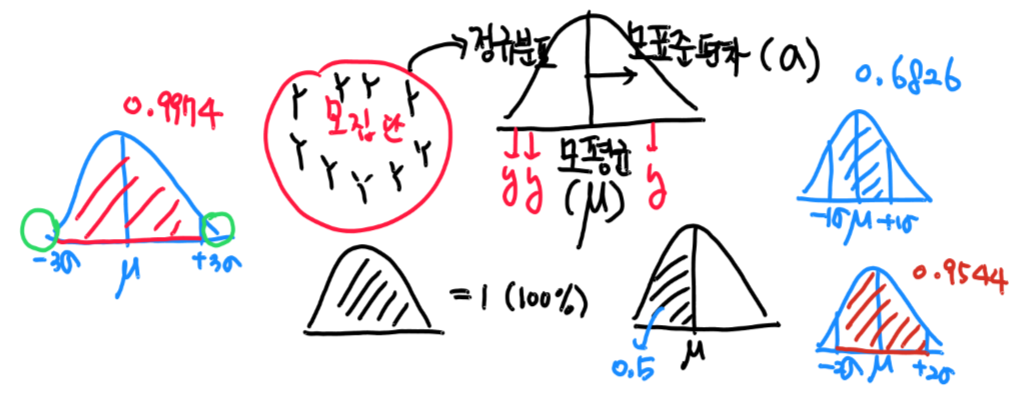
• 모집단의 수가 적을 경우, 평균을 내고 편차를 구하는데 많은 비용이 들지 않지만 무수히 많은 숫자를 처리하는데 한계가 있어서 표본을 뽑아내어 분석을 실시함

2) 표본 평균

• 표본 평균의 평균 = 모평균

• 표본 평균의 표준편차 = 모표준편차 / 루트 n (표본의 개수)

  중심극한정리 (CLT; Central Limit Theorem)
  : 모집단이 정규분포가 아닐 때, 표집을 무한에 가깝게 반복하면 표본 평균의 분포가 정규 분포에 가까워진다는 정리

  

3) 표준화

• 정규분포를 따르지만 평균과 표준편차가 각각 다를 때, 평균이 0이고 표준편차가 1인 확률변수 Z로 변환
  

3. 가설검정

• 모집단에 대한 입장에 대해 표본을 추출하여 수집된 데이터에 근거하여 통계적으로 검정하는 것

  모수 (Parameter)
  : 모집단을 나타내는 수치 (평균, 중위수, 최빈값 등)
  통계량 (Statistic)
  : 표본을 나타내는 수치 (평균, 중윗, 최빈값 등)

1) 귀무가설

• 모집단에 대한 기존의 입장
• Null Hypothesis, 영가설

2) 대립가설

• 모집단에 대한 새로운 입장
• Alternative Hypothesis, 대안가설, 연구가설

3) EDA; Exploratory Data Analysis

• 유연하고 탐색적 사고를 바탕으로 데이터를 바라보는 것

4) 유의확률 (P-Value)

• 표본에서 관찰한 값이 귀무가설이 맞다는 가정 하에 얼마나 일어났는지 알려줌
  ex) P-value가 크다 -> 표본은 쉽게 일어난다

  ① 유의수준(0.05) > 유의확률(0.01) : 채택 결정 시 실수 할 확률(5%)이 기각 결정 시 실수할 확률(1%)보다 크다. 따라서 실수 확률이 높은 결정을 하면 안된다. → 실수확률이 낮은 “기각” 결정을 해야 한다.
  ② 유의수준(0.05) < 유의확률(0.15) : 채택 결정 시 실수 할 확률(5%)이 기각 결정 시 실수할 확률(15%)보다 작다. 따라서 실수 확률이 높은 결정을 하면 안된다. → 실수확률이 낮은 “채택” 결정을 해야 한다.
  출처 - https://m.blog.naver.com/PostView.nhn?blogId=smblaw&logNo=220055506019&proxyReferer=https:%2F%2Fwww.google.com%2F

• 유의확률이 크면 귀무가설!!!

5) 가설검정 과정