1. 개요

• 데이터 값은 평균과 같은 일정한 값으로 돌아가려는 경향성을 이용

• 기본적으로 선형이라는 전제하에 점들을 가장 잘 설명하는 직선을 찾고 경향성을 설명

• 종속변수와 독립변수 간에 선형관계가 존재하는지 알 수 있음

• 독립변수의 종속변수에 대한 유의성과 영향력의 정도를 알 수 있음.

• 추정된 회귀모형을 통해 종속변수의 예측치를 알 수 있음

1) 회귀 계수

• 머신러닝의 관점에서 피처(독립변수)와 결정 값(종속변수) 데이터로 학습을 통해 최적의 회귀계수를 구함
• 회귀 계수의 값에 따라 독립변수가 종속변수에 미치는 영향의 크기를 검정

2. 단순회귀분석 (Simple)

• 하나의 종속변수에 대해 독립변수가 하나인 경우

1) Regression Model (회귀 모형)

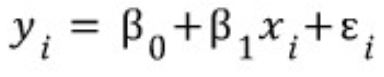
• 일차함수 형태로 마지막 항을 랜덤오차라 함
• 위의 랜덤오차를 최소화하고 회귀계수 (beta0(y절편)와 beta1(기울기))를 구해야 함
• 직선과 데이터의 차이가 평균적으로 가장 작아지는 직선이 좋은 추정\

  SST = SSR + SSE
  : 잔차의 제곱합을 최소화하는 방법으로 회귀계수 추정
  : SSE가 작을수록 분석을 잘한 것

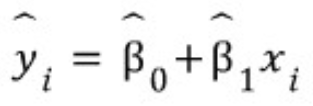
• 모집단의 모든 데이터를 다루는것은 불가능하기 때문에 표본으로 적합회귀선을 구함

• 잔차 (Residual)
  : 예측값 - 실제값

2) 회귀분석 정확도 평가

• R^2는 RSE의 단점을 보완한 평가지표 0 ~ 1의 범위 (SSR / SST)
• R^2가 1에 가까울수록 선형회귀 모형의 설명력이 높은 것을 의미
  

  수정된 결정계수
  : 독립변수 개수가 많아질수록 커지는 결정계수의 단점을 보완해 표본의 크기와 독립변수의 수를 고려

3. 다중회귀분석 (Multiple)

• 하나의 종속변수에 대해 독립변수가 둘 이상인 경우
  
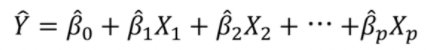
• 단순회귀분석과 동일하게 각각의 회귀계수가 통계적으로 유의미한지 검정하지만 잔차의 정규성이라는 가정을 만족할 때, t 통계량의 절대값이 크거나 대응되는 p-value가 더 작다면 독립변수와 종속변수 사이의 선형관계가 더 강함을 의미

1) 다중공선성 (Multicollinearity)

• x들간의 직선의 관계를 의미하는데 다중공선성을 최소화 시킬 수 있도록 독립변수 선택을 해야 함
• 예측의 정확도가 하락하는 문제점 발생
• VIF (Variance inflation factor), 변수 간의 correlation 등으로 진단
  
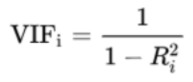
• VIF >= 10 이면 다중공선성이 존재하는 변수로 판단
• 다중공선성이 높을 경우, 중요한 독립변수를 제외하고 다른 변수를 제거하는 방법이 존재
• 다만, VIF가 높더라도 통계적 유의미한 변수라면 제거하지 않는 것이 적절함

  과적합(Overfit)
  : 복잡하고 데이터가 적을수록 다수 발생

2) 더미변수

(1) 특징

• 0 또는 1의 값을 가짐
• 질적변수의 개수보다 1개 적게 만들어짐
• 회귀식의 기울기를 바꾸지 않고 절편만을 바꾸어 평행하게 움직이는 역할을 함

(2) 만드는 법

• 질적변수 중 기준이 되는 변수 설정
• 기준이 되는 변수 제외하고 더미변수를 만듬 (의미에 해당하면 1, 하지 않으면 0)

3) 변수선택

(1) 전진선택법 (forward selection)

• 절편만 있는 상수모형에서 영향력이 클 것으로 예상되는 독립변수부터 추가하여 평가
• 장점 : 직관적이고 변수가 많아도 사용가능
• 단점 : 변수값의 작은 변동에 결과값이 크게 변동

(2) 후진제거법 (backward selection)

• 가장 적은 영향을 주는 변수부터 하나씩 제거
• 장점 : 선택 시, 전체 변수들을 이용
• 단점 : 변수의 개수가 많은 경우 사용하기 용의하지 않음

(3) 단계선택법 (stepwise selection)

• 전진선택법에서 단계별로 변수를 추가, 제거하며 유의미한 결과가 나올때까지 평가

(4) 정보량 규준

• 손실 가중치 계산 법에 따라 AIC (Akaike Information Criterion), BIC (Bayesian Information Criterion) 두 가지 방법을 사용
• 우도 (Likelihood)를 가장 크게 하고 변수 갯수는 가정 적은 모델을 의미
• BIC는 AIC보다 변수 증가에 민감해서 변수 갯수가 작은 것이 우선이면 BIC 참고하는 것이 좋음
• 둘 다 값이 작을 수록 올바른 모형에 유사
  

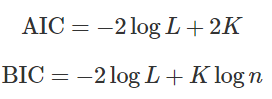
(5) 비표준화 계수와 표준화 계수

• 독립 변수들 간의 단위들이 서로 다르다면 각 회귀계수를 통계적으로 유의미한 비교 불가
• 다만, 표준화 계수값이 크다고 해서 더 중요한 변수가 아니고 결정계수(R^2)로 확인해야함