1. 단순선형 회귀분석

import statsmodels.api as sm

model = sm.OLS(endog = Y, exog = X).fit()
model.summary()

# OLS   : Ordinary Least Square의 약자
# endog : endogenous : 내생의
# exog  : exogenous  : 외생의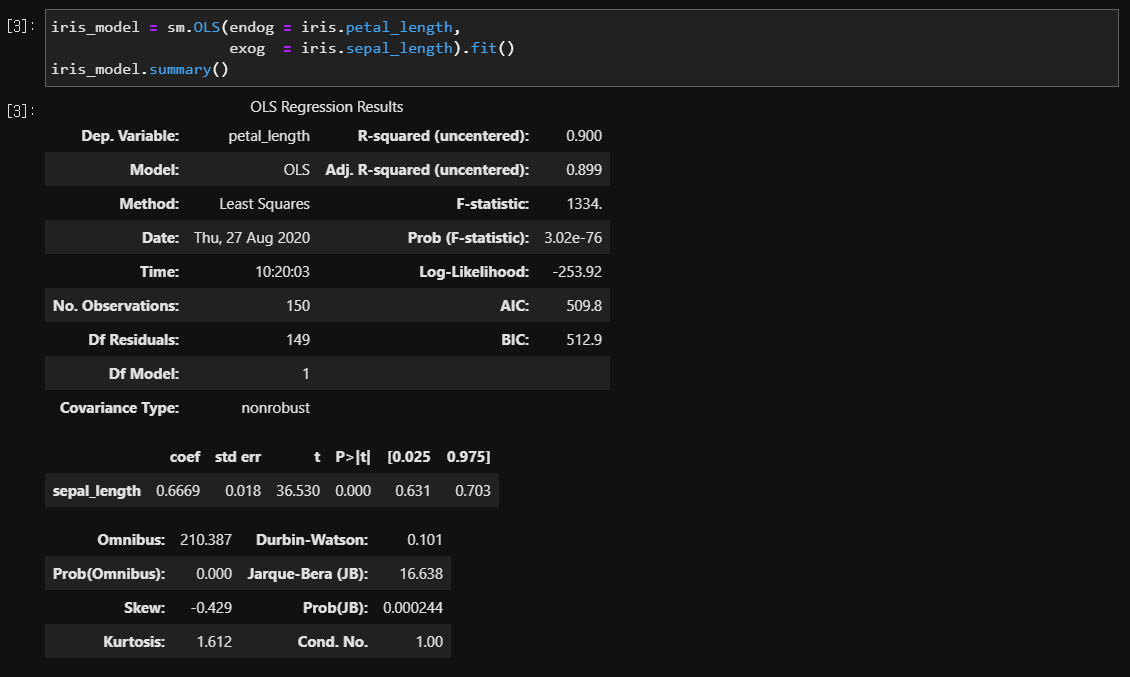

1) 회귀모형은 타당한가?

• 귀무가설 : 회귀모형은 타당하지 않다.
• 대립가설 : 회귀모형은 타당하다.

결과

• F-statistic : 검정통계량 = 1334
• Prob (F-statistic) : P-value = 0.000
• 유의확률이 0.000이므로 유의수준 0.05에서 회귀모형은 통계적으로 유의하게 타당한 것으로 나타났다.

2) X는 Y에게 유의한 영향을 주는가?

• 귀무가설 : X는 Y에게 영향을 주지 않는다.
• 대립가설 : X는 Y에게 영향을 준다.

결과

• coef : 회귀계수 (beta_1) = 0.667
• std err : 표준오차 (standard error) = 0.018
• t : 회귀계수 / 표준오차 = 0.667 / 0.018 = 36.530
• P > |t| : P-value = 0.000
• 유의확률이 0.000이므로 유의수준 0.05에서 꽃받침의 길이는 꽃잎의 길이에 통계적으로 유의한 영향을 주는 것으로 나타났다.

3) X는 Y에게 어떤 영향을 주는가?

• 회귀계수의 값이 크면 X가 Y에게 많은 영향을 준다.
• 회귀계수의 값이 작으면 X가 Y에게 작은 영향을 준다.
• 회귀계수의 부호가 +이면 X가 Y를 증가시키는 영향을 준다.
• 회귀계수의 부호가 -이면 X가 Y를 감소시키는 영향을 준다.

결과

• coef : 회귀계수 = 0.667
• 꽃받침의 길이가 1cm 증가하면 꽃잎의 길이는 약 0.667cm 증가시키는 영향을 준다.

4) 회귀모형의 설명력 or X의 설명력

• Y의 다름(변동)을 회귀모형이 얼마나 설명하고 있는가?
• Y의 다름(변동)을 X가 얼마나 설명하고 있는가?

결과

• R-squared (uncentered) = 0.900
• 회귀모형이 Y의 다름(변동)을 약 90.0% 정도 설명하고 있다.
• X가 Y의 다름(변동)을 약 90.0% 정도 설명하고 있다.

  R-square
  : 결정계수
  : SSR / SST : 0 ~ 1
  : 값이 크면 회귀모형이 좋은 것으로 판단하는 지표 중에 하나

MSE

from sklearn.metrics import mean_squared_error

mean_squared_error(y_true = , y_pred = )

• 회귀 모델의 적합도를 나타내는 척도로 0에 가까울 수록 적합도가 높음

5) 예측 (Prediction)

model.predict(exog = X)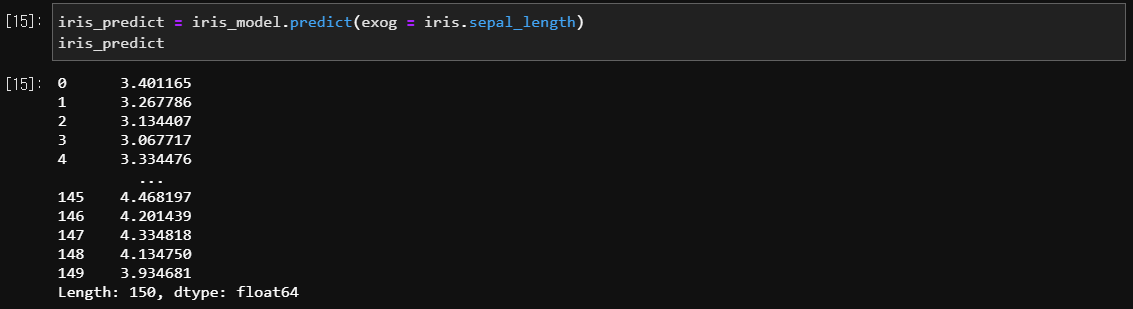

2. 회귀모형의 진단 or 가정

1) 오차의 정규성 가정

• 귀무가설 : 정규분포를 따른다.
• 대립가설 : 정규분포를 따르지 않는다.
• Jarque-Bera Normality test
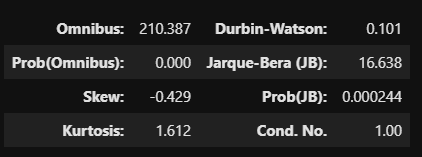
• Jarque-Bera (JB) = 16.638
• Prob (JB) = 0.000244
• 유의확률이 0.000이므로 유의수준 0.05에서 정규성 가정이 깨짐

2) 오차의 독립성 가정

• 귀무가설 : 독립이다.
• 대립가설 : 독립이 아니다.
• Durbin-Watson = 0.101

  DW 값이 2에 가까우면 오차들은 독립
  DW 값이 0에 가까우면 독립 X, 양의 자기상관 O
  DW 값이 4에 가까우면 독립 X, 음의 자기상관 O

# 참고
import statsmodels.stats as sms

sms.durbin_watson(residuals)

3) 회귀모형의 유의성 검정

• 귀무가설 : 유의하지 않다.
• 대립가설 : 유의하다.
• 독립변수들을 회귀모형에 적용했을 때, 회귀모형의 유의성 검정
• Omnibus = 210.387
• Prob(Omnibus) = 0.000
• 유의확률이 0.000이므로 유의수준 0.05에서 독립변수들을 적용했을 때, 통계적으로 유의하다.

4) 오차에 대한 등분산 검정

• 귀무가설 : 등분산이다.
• 대립가설 : 등분산이 아니다.

  stats.bartlett(X, residuals)

  
• 유의확률이 0.000이므로 유의수준 0.05에서 등분산 가정이 깨짐