일반적인 RNN을 Vanilla RNN이라 함.
Vanilla RNN의 한계를 극복하기 위해 LSTM이 탄생.
Limit of Vanilla RNN
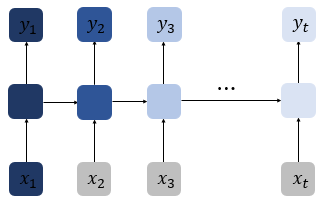
Vanilla RNN은 이전 시점의 출력 벡터에 의존적.
타임 스텝이 길어질 수록 초기의 정보가 뒤로 충분히 전달되지 못하는 gradient vanishing 현상 발생.
초기의 정보가 중요할 경우 문제 발생.
이를 장기 의존성 문제 (the problem of Long-Term Dependencies)라 함.
Architecture
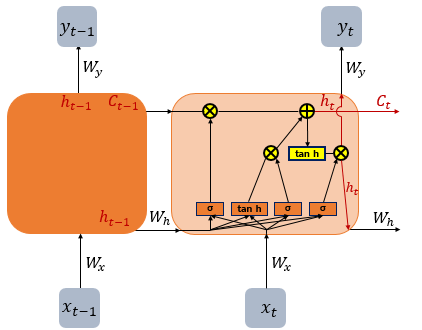
은닉측의 메모리 셀에 Input gate, Forget gate, Output gate를 추가하여 불필요한 정보를 삭제하고 중요한 정보를 기억.
이를 위해 셀 상태 (Ct)를 추가.
이러한 LSTM은 RNN과 비교하여 긴 시퀀스의 입력 처리에 탁월.
Concept
wxi, wxg, wxf wxo : xt에 관한 gate에서의 가중치
whi, whg, whf, who : ht−1에 관한 gate에서의 가중치
bi, bg, bf, bo : bias
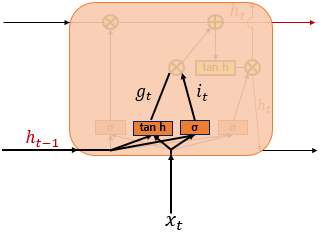
Input gate는 현재 정보를 기억.
it=σ(wxixt+whiht−1+bi)∈[0,1]
gt=tanh(wxgxt+whght−1+bg)∈[−1,1]
it, gt로 기억할 정보의 양을 정함.
Forget Gate
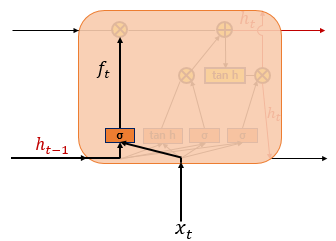
Forget gate는 기억을 삭제.
ft=σ(wxfxt+whfht−1+bf)∈[0,1]
0에 가까울수록 많은 기억 삭제, 1에 가까울수록 기억 보존.
Cell State Ct
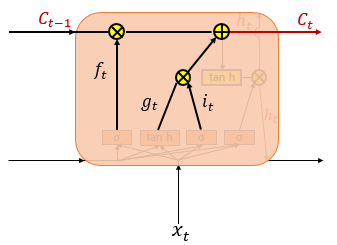
Ct=ft∘Ct−1+it∘gt
it∘gt : 기억할 정보의 양
Forget Gate ft=0
t−1 시점의 셀 상태 Ct−1의 영향력은 0.
즉, Ct=it∘gt.
Input gate의 결과가 t 시점의 셀 상태.
⇔ Open input gate, Close forget gate.
Input Gate it∘gt=0
t−1 시점의 셀 상태 Ct−1의 영향력에만 의존.
즉, Ct=Ft∘Ct−1.
t−1 시점의 결과가 t 시점의 셀 상태.
⇔ Open forget gate, Close input gate.
Open gate는 t 시점의 입력의 양을, Forget gate는 t−1 시점의 입력의 양을 반영.
Output Gate
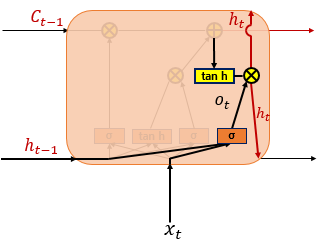
ot=σ(wxoxt+whoht−1+bo)∈[0,1]
ht=ot∘tanh(Ct)∈[−1,1]
t 시점의 은식 상태를 결정.
Reference
2) 장단기 메모리(Long Short-Term Memory, LSTM)






