SVM은 분류 및 회귀 분석을 위한 지도 학습 모델.
큰 데이터 셋에 대해서는 작동하지 않아, 딥러닝에 밀리고 있는 추세.
Concept
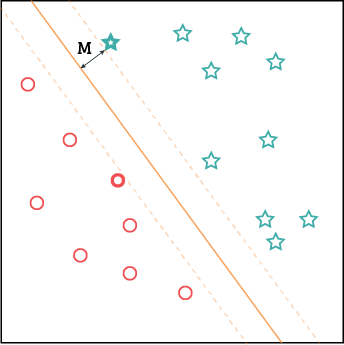
복수의 클래스 벡터를 선형으로 분류하는 것이 기본.
Decision Boundary : 클래스를 분류해주는 경계
※ 차원의 관점에서 이는 Hyperplane
Supprot Vector : decision boundary에서 가장 가까운 최외곽 벡터
Margin (M) : decision boundary에서 support vector까지의 거리
Margin을 최대로 하는 경계를 찾는 것이 최종 목표.
Detail
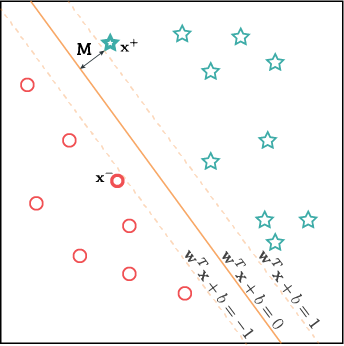
w : normal vector of hyperplane
x+ : (support) vetor of positive class
x− : (support) vetor of negative class
decision boundary를 결정하기 위해서는 hyperplane을 결정해야 함.
Hyperplane : wTx+b=0
즉, w와 b를 결정해야 함.
Hard Margin
거리 δ에 대해서,
wTx++b≥δ, wTx−+b≤δ
Normalize by δ,
wTx++b≥1, wTx−+b≤−1
For ti=1 if x+ else −1 if x−,
ti(wTx+b)−1≥0 (support vector를 지날 경우, 등호 성립)
Margin M : (x+−x−)⋅∣∣w∣∣w=∣∣w∣∣2
∴maximize ∣∣w∣∣2 ⇔minimize 21∣∣w∣∣2 subject to ti(wTxi+b)−1≥0
KKT (Karush-Kuhn-Tucker) Conditions
optimize f(x) subject to gi(x)≤0, hj(x)=0
1) Stationarity
∇f(x∗)+∑μi∇gi(x∗)+∑λj∇hj(x∗)=0
2) Primal Feasibility
gi(x)≤0, hj(x)=0
3) Dual Feasibility
μi≥0
4) Complementary Slackness
μigi(x∗)=0
KKT 조건을 적용해보면,
minimize f(w)= 21∣∣w∣∣2 subject to gi(w)=ti(wTxi+b)−1≥0
1) ∇f(w∗)+∑αi∇gi(w∗)=0
2) gi(w)=ti(wTxi∗+b)−1≥0
3) αi≥0
4) αigi(w∗)=αi(ti(w∗Txi∗+b)−1=0
Lagrangian에 의해,
L(w,b,α)= 21∣∣w∣∣2−∑αi[ti(wTxi+b)−1]
∂w∂L =w∗−∑αitixi=0
∂b∂L =∑αiti=0
∴L(w∗,b∗,α)=∑αi−21∑∑αiαjtitjxiTxj
minimize L(w,b,α) ⇔ maximize L(w∗,b∗,α) ⇔ maximize Ldual(α)
① 이를 통해 α를 구함.
② w∗=∑αitixi
③ b∗= Ns1∑(tj−∑αitixiTxj)
Soft Margin
hyperplane에 의해 깔끔하게 분류되지 않음.
slack varialbe ξi를 통해 오류 허용을 조절.
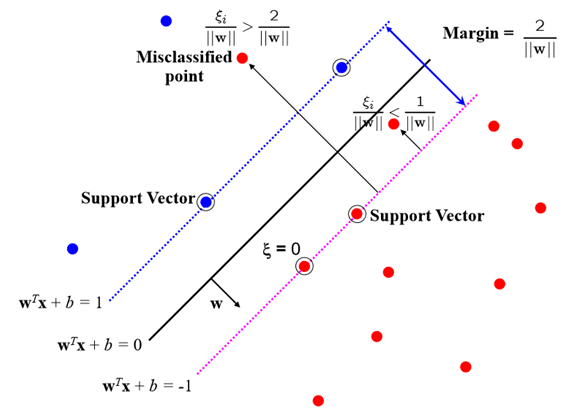
minimize f(w)= 21∣∣w∣∣2+C∑ξi
subject to gi(w)=ti(wTxi+b)≥1−ξi, ξi≥0
ξi=0 : 분류 성공
ξi>1 : 분류 실패
0<ξi<1 : margin violation
Dual 문제를 적용하면
maximize Ldual(α)=∑αi−21∑∑αiαjtitjxiTxj
subject to ∑αiti=0 for 0≤αi≤C
C가 작을수록 margin은 커지고, 더 많은 오류 허용.
C가 클수록 margin은 작아지고, 더 적은 오류 허용.
Kernel
선형으로 분류하지 못할 경우, kernel 사용.
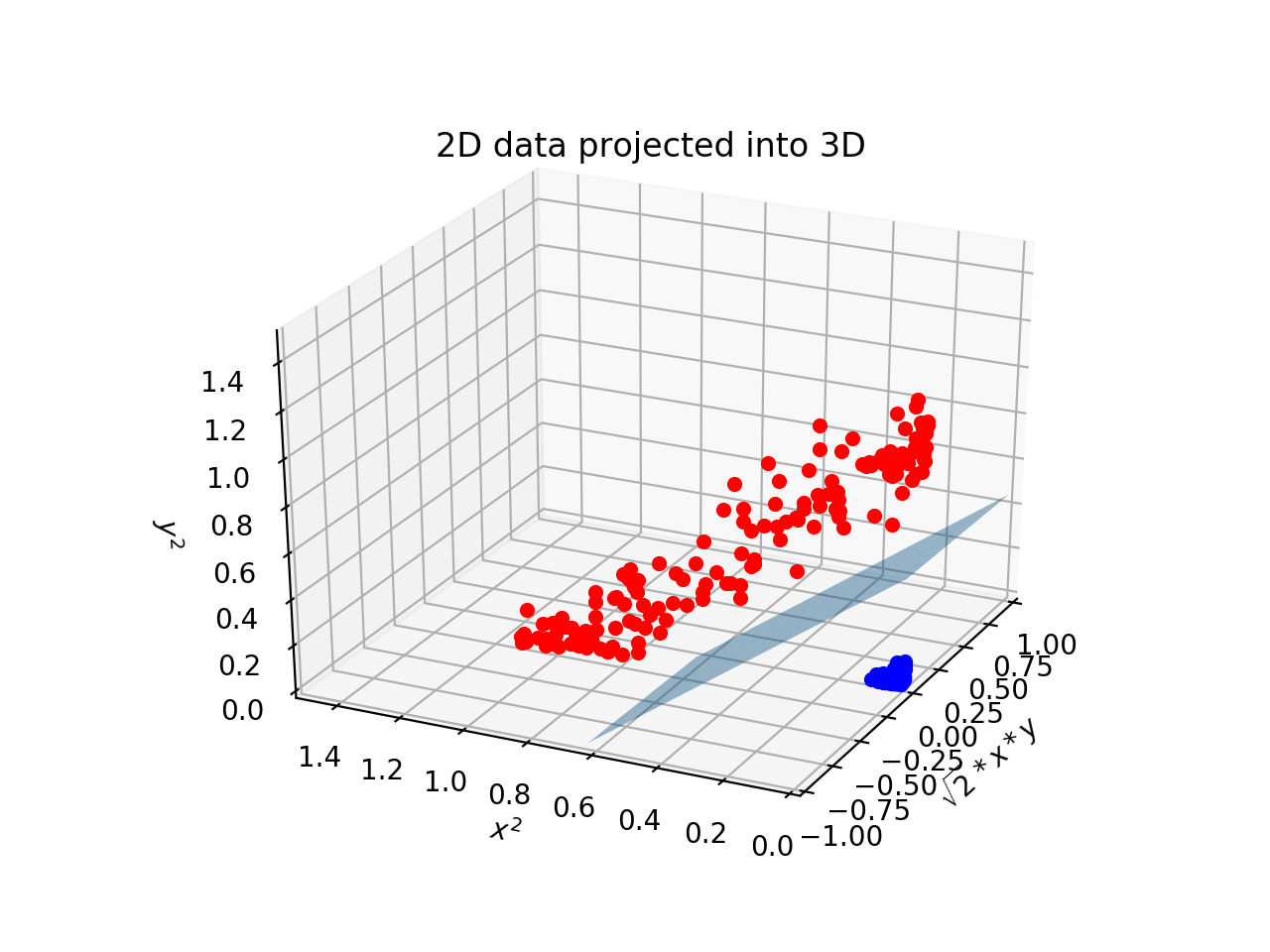
데이터를 더 높은 차원으로 mapping (Φ)하여 hyperplane 결정.
maximize Ldual(α)=∑αi−21∑∑αiαjtitjΦ(xi)TΦ(xj)
Φ(xi)TΦ(xj)을 kernel이라 함.
머서의 정리에 의해,
maximize Ldual(α)=∑αi−21∑∑αiαjtitjK(xi,xj)
머서의 정리
함수 K(a,b)가 머서의 조건을 만족하면, a와 b를 더 높은 차원으로 mapping하는 K(a,b)=Φ(a)TΦ(b)를 만족하는 함수 Φ
가 존재.
따라서 Φ를 계산하지 않더라도 존재함을 알기 때문에, K를 커널로 사용.
커널 종류
Linear : K(a,b)=aT⋅b
Polynomial : K(a,b)=(γaT⋅b+r)d
Gaussian RBF : K(a,b)=exp(−γ∣∣a−b∣∣2)
Sigmoid : K(a,b)=tanh(γaT⋅b+r)
Gaussian Radial Bias Fnction
K(a,b)=exp(−γ∣∣a−b∣∣2)
2차원의 점을 무한한 차원의 점으로 mapping.
γ가 작을수록 표준편차가 커져서, decision boundary가 단조로움. ⇒ Underfitting
γ가 클수록 표준편차가 작아져서, decision boundary가 복잡해짐. ⇒ Overfitting
Reference
[학부생의 머신러닝] | General | SVM : Support Vector Machine
SVM(Support Vector Machine) 원리
[머신러닝] 9. 머신러닝 학습 방법(part 4) - SVM(1)
서포트 벡터 머신(Support Vector Machine) 쉽게 이해하기
Kernel/Kernel trick(커널과 커널트릭)




