가설 검정

1. 가설검정과 유의수준 정의

• 가설 검정 = 가설(Hypothesis) + 검정(Testing)

• 가설(hypothesis)
  주어진 사실 또는 조사하려고 하는 사실에 대한 주장 또는 추축을 가설이라고 함
  통계학에서는 특히 모수를 추청 할 때 모수가 어떠하다는 증명하고 싶은 추축이나 주장을 가설이라고 함

• 귀무 가설(Null hypothesis: $H_0$ )
  기존의 사실(아무것도 없다, 의미가 없다)
  대립가설과 반대되는 가설로 연구하고자 하는 가설의 반대의 가설로 귀무 가설은 연구 목적이 아님
  Ex) $H_0$ : 코로나 백신이 효과가 없다 , $H_0$ : $\mu$ = 0

• 대립 가설(Alternative hypothesis: $H_1$ )
  데이터로 부터 나온 주장하고 싶은 가설 또는 연구의 목적으로 귀무가설의 반대
  Ex) $H_1$ : 코로나 백신이 효과가 있다 , $H_0$ : $\mu \not= 0$ $or$ $\mu \geq 0$

• 제1종 오류(type I error)
  귀무가설이 참이지만, 귀무가설을 기각하는 오류
  $H_0$ 를 기각할 확률이 $\alpha$ 라고 하면 채택하게 될 확률은 $1-\alpha$ 로 표시할 수 있음
  제1종 오류를 범할 확률의 최대허용 한계를 유의수준이라고 하며, $\alpha$ 라고 표시

• 제2종 오류(type II error)
  귀무가설이 기각해야 하지만, 귀무가설을 채택하는 오류

• 검정통계량
  귀무가설이 참이라는 가정하에 얻은 통계량
  검정결과 대립가설을 선택하게 되면 귀무가설을 기각(reject)함
  검정결과 귀무가설을 선택하게 되면 귀무가설을 기각하지 못한다고 표현함

• P-value
  귀무가설이 참일 확률
  0~1사이의 표준화된 지표(확률값)
  귀무가설이 참이라는 가정하에 통계량이 귀무가설을 얼마나 지지 하는지를 나타낼 확률

• 기각역(reject region)
  귀무가설을 기각시키는 검정통계량의 관측값의 영역

• 가설 검정의 절차

  1. 가설 수립: $H_0$ : 코로나 백신이 효과가 없다, $H_1$ :코로나 백신이 효과가 있다
  2. 유의 수준 결정: 유의 수준 $\alpha$ 정의
  3. 기각역 설정
  4. 검정통계량 계산
  5. 의사 결정

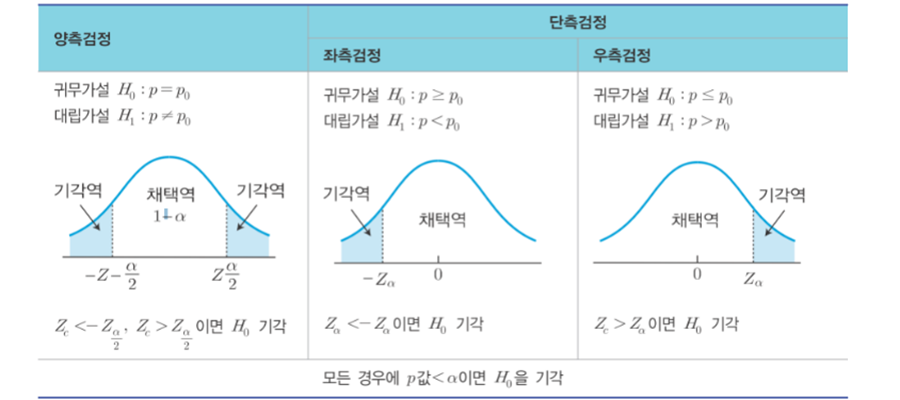
• 양측검정(two-side test)
  대립가설의 내용이 같지 않다 또는 차이가 있다 등의 양쪽 방향의 주장
  -A백신과 B백신의 코로나 면역력에는 차이가 있다
  -A팀과 B팀의 평균 연봉은 차이가 있다

• 단측검정(one-side test)
  한쪽만 검증하는 방식으로 대립가설의 내용이 크다 또는 작다 처럼 한쪽 방향의 주장
  -A제품의 수율이 B제품의 수율보다 크다
  -A팀의 평균 연봉이 B팀의 평균 연봉보다 크다
  

2. 단일 표본에 대한 가설 검정

• 모평균 가설검정 – 모분산을 아는 경우

  • 가설
    a) $H_0$ : $\mu$ = $\mu_0$ vs $H_0$ : $\mu$ $\not=$ $\mu_0$
    b) $H_0$ : $\mu$ = $\mu_0$ vs $H_0$ : $\mu$ $\gt$ $\mu_0$
    c) $H_0$ : $\mu$ = $\mu_0$ vs $H_0$ : $\mu$ $\lt$ $\mu_0$

  • 유의수준 : $\alpha$ = 0.05, 검정통계량 : $Z = \frac{\bar X - \mu}{\sigma / \sqrt n} \sim N(0,1)$

  • 검정통계량 관측값 : $z_0 = \frac{\bar X - \mu_0}{\sigma / n}$
    a) $|z_0| \geq z_{\frac{\alpha}{2}}$ 이면 $H_0$ 기각
    b) $z_0 \geq z_\alpha$ 이면 $H_0$ 기각
    c) $z_0 \leq -z_\alpha$ 이면 $H_0$ 기각

• 모평균 가설검정 – 모분산을 모르는 경우(소표본)

  • 가설
    a) $H_0$ : $\mu$ = $\mu_0$ vs $H_0$ : $\mu$ $\not=$ $\mu_0$
    b) $H_0$ : $\mu$ = $\mu_0$ vs $H_0$ : $\mu$ $\gt$ $\mu_0$
    c) $H_0$ : $\mu$ = $\mu_0$ vs $H_0$ : $\mu$ $\lt$ $\mu_0$

  • 유의수준 : $\alpha$ = 0.05, 검정통계량 : $T = \frac{\bar X - \mu}{\sigma / \sqrt n} \sim t(n-1)$

  • 검정통계량 관측값 : $t_0 = \frac{\bar X - \mu_0}{\sigma / n}$
    a) $|t_0| \geq t_{\frac{\alpha}{2}}(n-1)$ 이면 $H_0$ 기각
    b) $t_0 \geq t_\alpha(n-1)$ 이면 $H_0$ 기각
    c) $t_0 \leq - t_\alpha(n-1)$ 이면 $H_0$ 기각

• 모비율 가설검정

  • 가설
    a) $H_0$ : $\hat p$ = $p_0$ vs $H_1$ : $\hat p$ $\not=$ $p_0$
    b) $H_0$ : $\hat p$ = $p_0$ vs $H_1$ : $\hat p$ $\gt$ $p_0$
    c) $H_0$ : $\hat p$ = $p_0$ vs $H_1$ : $\hat p$ $\lt$ $p_0$

  • 유의수준 : $\alpha$ = 0.05, 검정통계량 : $z = \frac{\hat p - p}{\sqrt{\frac{p(1-p)}{n}}} \sim N(0,1)$

  • 검정통계량 관측값 : $z_0 = \frac{\hat p - p_0}{\sqrt{\frac{p_0(1- p_0)}{n}}}$

3. 두개의 표본에 대한 가설 검정

• 대표본 – 모분산을 아는 경우

  • 가설
    a) $H_0 : \mu_1 = \mu_2$ VS $H_0 : \mu_1 \not= \mu_2$
    b) $H_0 : \mu_1 = \mu_2$ VS $H_0 : \mu_1 \gt \mu_2$
    c) $H_0 : \mu_1 = \mu_2$ VS $H_0 : \mu_1 \lt \mu_2$

  • 유의수준 : $\alpha$ = 0.05, 검정통계량 : $Z = \frac{(\bar X_1 - \bar X_2)-(\mu_1 - \mu_2)}{\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}} \sim N(0,1)$

  • 검정통계량 관측값 : $z_0 = \frac{(\bar X_1 - \bar X_2)}{\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}$
    a) $|z_0| \geq z_{\frac{\alpha}{2}}$ 이면 $H_0$ 기각
    b) $z_0 \geq z_\alpha$ 이면 $H_0$ 기각
    c) $z_0 \leq -z_\alpha$ 이면 $H_0$ 기각

• 소표본 – 모분산을 모르는 경우

  • 가설
    a) $H_0 : \mu_1 = \mu_2$ VS $H_0 : \mu_1 \not= \mu_2$
    b) $H_0 : \mu_1 = \mu_2$ VS $H_0 : \mu_1 \gt \mu_2$
    c) $H_0 : \mu_1 = \mu_2$ VS $H_0 : \mu_1 \lt \mu_2$

  • 유의수준 : $\alpha$ = 0.05, $S_p^2 = \frac{(n_1 -1)s_1^2 + (n_2 -1)s_2^2}{n_1 + n_2 - 2}$

    검정통계량 : $T = \frac{(\bar X_1 - \bar X_2)-(\mu_1 - \mu_2)}{s_p \sqrt{\frac{1}{n_1}+\frac{1}{n_2}}} \sim t(n_1 + n_2 -2)$

  • 검정통계량 관측값 : $T_0 = \frac{(\bar X_1 - \bar X_2)}{s_p \sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}$
    a) $|z_0| \geq z_{\frac{\alpha}{2}}$ 이면 $H_0$ 기각
    b) $z_0 \geq z_\alpha$ 이면 $H_0$ 기각
    c) $z_0 \leq -z_\alpha$ 이면 $H_0$ 기각

• 대응 비교

  • 쌍으로 조사된 자료 $(X_1,Y_1), (X_2,Y_2), \cdots, (X_i,Y_i)$ 가 주어 졌을 때 $X_i$ 의 평균을 $\mu_x, Y_i$ 의 평균을 $\mu_y$ 라고 하면 $$ 으로 정의하고 가설은 아래와 같음
  • 가설
    a) $H_0 : \mu_x = \mu_y$ VS $H_1 : \mu_x \not= \mu_y$ → $H_0 : \mu_D =0 VS H_1 : \mu_D \not= 0$
    b) $H_0 : \mu_x = \mu_y$ VS $H_1 : \mu_x \gt \mu_y$ → $H_0 : \mu_D =0 VS H_1 : \mu_D \gt 0$
    c) $H_0 : \mu_x = \mu_y$ VS $H_1 : \mu_x \lt \mu_y$ → $H_0 : \mu_D =0 VS H_1 : \mu_D \lt 0$

  • 유의수준 $\alpha$ = 0.05, 검정통계량 $T = \frac{D - \mu_D}{S_D \sqrt n} \sim t(n-1)$

  • 검정통계량 관측값 $T_0 = \frac{D - \mu_D}{S_D \sqrt n}$

    a) $|t_0| \geq t_{\frac{\alpha}{2}}$ 이면 $H_0$ 기각
    b) $t_0 \geq t_\alpha$ 이면 $H_0$ 기각
    c) $t_0 \leq -t_\alpha$ 이면 $H_0$ 기각