추정

1. 추정

1. 추정(estimation) : 모집단의 모수를 모를 경우 표본으로 추출된 통계량을 모집단의 근사값으로 사용하는 것을 추정이라고 함

2. 추정량(estimator) : 표본 평균으로 모평균을 추정할 때 표본 평균을 모평균에 대한 추정량이라고 함

3. 모수를 추정 하는 방법에는 점추정(point estimation) 과 구간 추정(interval estimation)이 있음

   • 점추정: 모수를 하나의 특정값으로 추정 하는 방법
   • 구간 추정: 모수가 포함될 수 있는 구간을 추정하는 방법
     

4. 점추정의 대표적인 성질

   • 일치성(Consistency)
     표본의 크기가 모집단의 크기에 근접해야 함
     표본이 크기가 크면 클수록(모집단에 가까울 수록) 추정량의 오차가 작아짐
   • 불편성(unbiased estimator)
     추정량이 모수와 같아야 함
     모수가 $\theta$ 이고 추정량이 $\hat{\theta}$ 라고 정의하면, $E[\hat{\theta}]=0$ 이고, 이를 불편 추정량 이라고 함
     즉, $E[\hat{\theta}]=0$ 일때의 추정량을 불편 추정량이라고 하고, 같지 않다면 편의(biased) 있다고 함
   • 유효성(efficiency)
     추정량의 분산이 최소값이어야 함
     모수에 대한 추정량의 분산이 작을 수록 추정량이 효율적이다는 의미임
     만약 모수 $\theta$ 의 불편 추정량이 $\hat{\theta_1}$, $\hat{\theta_2}$ 이라면 $Var[\hat{\theta_1}] \lt Var[\hat{\theta_2}]$ 이면, $\hat{\theta_1}$ 효율적인 추정량임
   • 평균오차제곱(Mean Squared Error, MSE)
     평균오차제곱이 최소값이어야 함
     $E[(\hat{\theta} - \theta )^2]=0$ 이 최소이어야 함

5. 구간추정: 모수가 포함될 수 있는 구간을 추정하는 방법

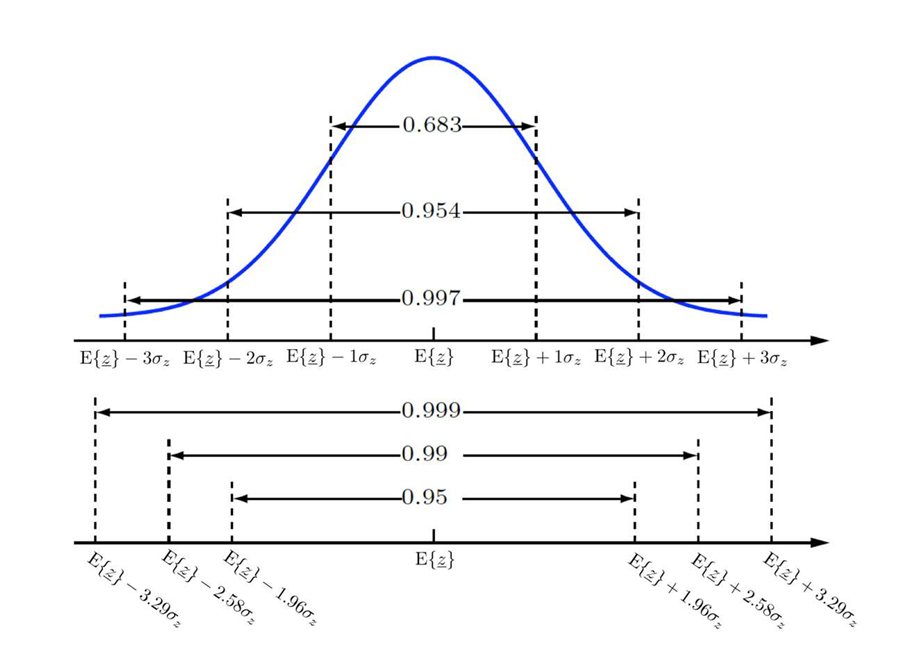
6. 신뢰구간(confidence level)
   추정값이 존재하는 구간에 모수가 포함될 확률

   • 신뢰 수준은 $100 * (1-a)$ 로 계산 하며, $a$ 는 오차 수준임
   • 신뢰 수준 95%라는 것은 구간 추정된 값의 오차가 발생할 확률이 5%라는 것을 의미함
   • 이 오차를 유의 수준(significant level)이라고 하며, p= 0.05라고 함
   • 신뢰구간은 신뢰 하한, 신뢰 상한으로 표시하며 아래와 같은 수식으로 표현 (추정하는 모수가 $\theta$ )
     $P[L(\hat{\theta}) \leq \theta \leq U(\hat{\theta})]=1-a$
   • 만약, 모평균 $\mu$ 를 추정한다면, 표본평균이 $\bar x$ 이고 표준오차가 $sd$ 라고 하면 신뢰구간은 아래와 같음
     $\bar x - z \cdot sd \leq \mu \leq \bar x + z \cdot sd$

7. 모평균의 구간 추정

• 모집단의 분산을 아는 경우
  $X_1, X_2, \dots, X_n \sim iid\ N(\mu, \sigma^2),\ \hat{\mu}= \bar X \sim N (\mu, \frac{\sigma^2}{n}),\ Z \sim N(0,1)$

• 모집단의 분산을 모르는 경우
  $X_1, X_2, \dots, X_n \sim iid\ N(\mu, \sigma^2),\ \ T=\frac{\bar X - \mu}{S / \sqrt n} \sim t(n-1)$

• 표본의 크기 결정
  허용오차(permissible error) : 추정한 값이 틀려도 허용할 수 있는 오차
  정규분포의 신뢰구간을 통해 허용 오차를 계산
  $n = (\frac{z_a / s*{\sigma}}{d})^2$ , $d$: 허용오차
  $P(|\bar X -\mu| \leq d) = 1-a$

2. 모비율 추정

1. 모비율의 점추정
   비율에 대한 추정으로 우리가 원하는 속성(class)에 속하면 ‘1’ 아니면 ‘0’일 때, 1의 속성을 갖는 것의 개수를 X라고 하면 X ~ B(n,p) 임
   이 때 모비율의 점추정량을 표본 비율(sample proportion)이라고 함 ($\hat p = X / n$)

   $E(\hat p) = E(\frac{x}{n}) = \frac{np}{n} = p$ , $Var(\hat p)= Var(\frac{X}{n})= \frac{np(1-p)}{n^2} = \frac{p(1-p)}{n}$

2. 모비율의 구간 추정
   모비율 구간 추정에서 정규분포의 근사가 가능한 대표본은 보통 np>5, n(1-p)>5 를 동시에 만족 해야 함
   N이 충분히 크면 C.L.T에 의해서 $Z= \frac{\hat p - p}{\sqrt{p(1-p)/n}} \sim N(0,1)$

3. 모평균 차이의 추정(점추정)
   $E(\bar X_1 - \bar X_2) = E(\bar X_1)-E(\bar X_2)= \mu_1 - \mu_2$

   $Var(\bar X_1 - \bar X_2) = Var(\bar X_1)-Var(\bar X_2)= \frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}$

4. 모평균 차이의 추정(구간추정: 대표본)

   $Z=\frac{(\bar X_1 - \bar X_2)-(\mu_1 - \mu_2)}{\sqrt{\sigma_1^2 / n_1 + \sigma_2^2/n_2}}\sim N(0,1)$

5. 모평균 차이의 추정(구간추정: 소표본, 모분산을 모르는 경우)
   두 모집단의 분산을 아는 경우에는 대표본과 동일하게 추정 가능하지만 모르는 경우에는 등분산 가정이 필요 (두 모집단의 분산이 같다는 가정이 필요 $\sigma_1^2 = \sigma_2^2 = \sigma^2$ )

   합동 분산 추정량(pooled variance estimator) : 공통 분산의 추정량

   $S_p^2 = \frac{(n_1 -1)S_1^2 + (n_2 -1)S_2^2}{n_1 + n_2 -2}$

   $T = \frac{(\bar X_1 - \bar X_2) - (\mu_1 - \mu_2)}{S_p \sqrt{1/ n_1 + 1/ n_2}}\sim T(n_1 + n_2 -2)$
   

6. 모비율 차이의 추정(점추정)

   $E(\hat{p_1} - \hat{p_2}) = E(\hat{p_1})-E(\hat{p_2}) = p_1 - p_2$

7. 모비율 차이의 추정(구간추정)

   $\frac{(\hat{p_1} - \hat{p_2})-p_1 -p_2}{\sqrt{\frac{p_1(1-p_1)}{n_1} + \frac{p_2(1-p_2)}{n_2}}} \sim Z(0,1)$