데이터의 이해

01. 통계학 정의

통계학(statistics)

산술적 방법을 기초로 하여, 주로 다량의 데이터를 관찰하고 정리 및 분석하는 방법을 연구하는 수학의 한 분야이다.
근대 과학으로서의 통계학은 19세기 중반 벨기에의 케틀레가 독일의 "국상학(國狀學, Staatenkunde, 넓은 의미의 국가학)"과 영국의 "정치 산술(Political Arithmetic, 정치 사회에 대한 수량적 연구 방법)"을 자연과학의 "확률 이론"과 결합하여, 수립한 학문에서 발전되었다.

기술통계학(descriptive statistics)

데이터를 수집하고 수집된 데이터를 쉽게 이해하고 설명할 수 있도록 정리 요약 설명하는 방법론

추론통계학(inferential statistics)

모집단으로 부터 추출한 표본 데이터를 분석하여 모집단의 여러가지 특성을 추측하는 방법론

02. 데이터의 이해

2-1 데이터와 그래프

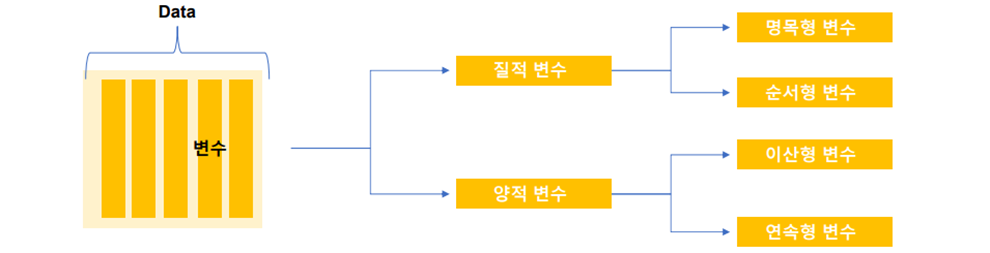
(1) 변수(Variable)

• 수학에서의 변수란, 어떤 정해지지 않은 임의의 값을 표현하기 위해 사용된 '기호' 이다. 보통 쉽게 설명하기 위해서 '변하는 숫자' 라는 표현을 자주 쓰고는 한다 (출처: 나무 위키)
• 통계학에서는 조사 목적에 따라 관측된 자료값을 변수라고 함, 해당 변수에 대하여 관측된 값들이 바로 자료(Data)가 됨

(2) 질적 자료

• 관측된 데이터가 성별, 주소지(시군구), 업종 등과 같이 몇 개의 범주로 구분하여 표현할 수 있는 데이터를 의미함
• 데이터 입력시 1은 남자, 2는 여자로 표현 가능하나 여기서 숫자의 의미는 없음(순서형 변수: 교육수준, 건강상태)

(3) 양적 자료

• 관측된 데이터가 숫자의 형태로 숫자의 크기가 의미를 갖고 있음
• 숫자를 표현할 때는 이산형 데이터와 연속형 데이터로 구분할 수 있음
  

(4) EDA(Exploratory Data Analysis)

• 데이터를 분석하는 과정 중에 가장 많이 사용하는 분석 방법
• 데이터를 탐색하는 분석 방법으로 도표, 그래프, 요약 통계 등을 사용하여 데이터를 체계적으로 분석하는 하나의 방법임
• 목적
  1. 데이터 분석 프로젝트 초기에 가설을 수립하기 위해 사용
  2. 데이터 분석 프로젝트 초기에, 적절한 모델 및 기법의 선정
  3. 변수 간 트렌드, 패턴, 관계 등을 찾고 통계적 추론을 기반으로 가정을 평가
  4. 분석 데이터에 적절한가 평가, 추가 수집, 이상치 발견 등에 활용

(5) 데이터 시각화(data visualization)

• 데이터 분석 결과를 쉽게 이해할 수 있도록 시각적으로 표현하고 전달되는 과정을
  말한다. 데이터 시각화의 목적은 도표(graph)라는 수단을 통해 정보를 명확하고 효과적으로 전달하는 것이다. (출처: wiki)
  

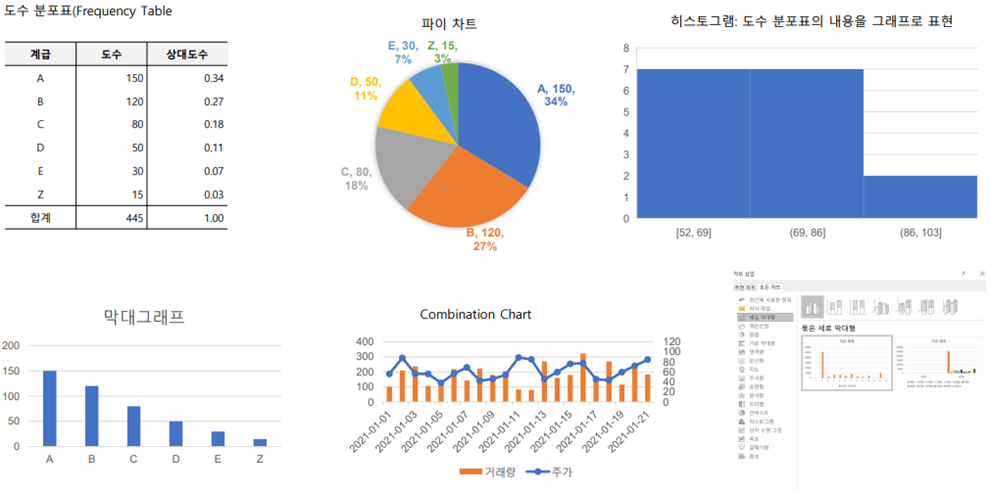
(6) 다양한 차트

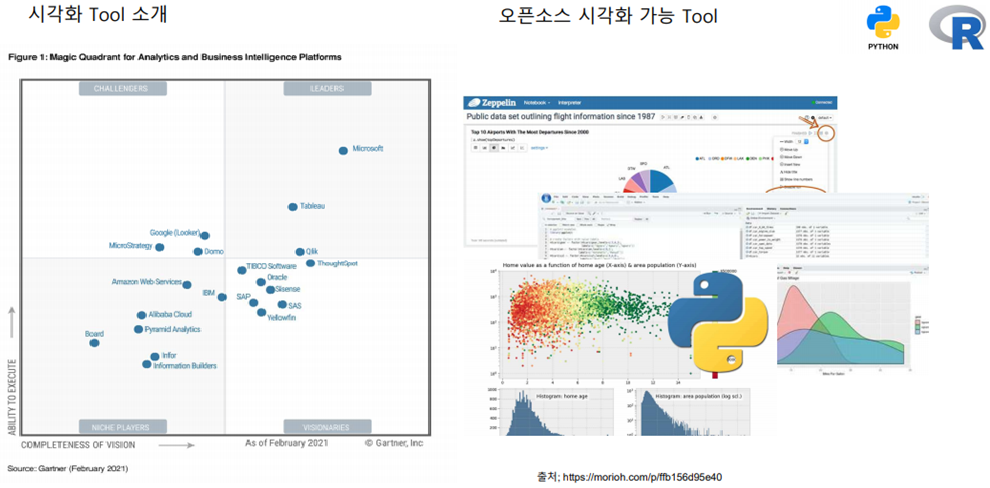
(7) 시각화 Tool

2-2 데이터의 기초 통계량

1 ) 기초 통계량

• 통계량(statistic)은 표본으로 산출한 값으로, 기술 통계량이라고도 표현함
• 통계량을 통해 데이터(표본)가 갖는 특성을 이해 할 수 있음

2 ) 중심 경향치

• 표본(데이터)를 이해하기 위해서는 표본의 중심에 대해서 관심을 갖기 때문에 표본의 중심을 설명하는 값을 대표값이라 하며 이를 중심경향치라고 함

• 대표적인 중심 경향치는 평균이며, 중앙값, 최빈값, 절사 평균 등이 있음

  (1) 평균(mean)

  • 평균은 모집단으로 부터 관측된 n개의 x가 주어 졌을때 아래와 같이 정의됨

    $\bar{x} = \frac{x_1+x_2+...+x_n}{n} = \frac{1}{n} \sum_{i=1}^{n} x_i$

  • 평균은 표본으로 추출된 표본 평균(sample mean, $\bar{x}$ 로 표기)이라고하며, 모집단의 평균을 모평균이라고 하며 $\mu$ 라고 표기함

  (2) 중앙값(median)

  • 평균과 같이 자주 사용하는 값으로 표본으로 부터 관측치를 크기순으로 나열 했을 때, 가운데 위치하는 값을 의미함

  • 관측치가 홀수 일 경우 중앙에 취하는 값이고, 짝수 일 경우 가운데 두개의 값을 산술 평균한 값임

  • 이상치가 포함된 데이터에 대해서 사용함

  • 관측치를 크기순으로 $x_1, x_2,..., x_n$ 나열 했을 때, 중앙값 m은

    $m = \left\{\begin{array}{l} x_{k+1}, \quad n = 2k + 1 \\ \frac{x_k + x_{k+1}}{2}, \quad n = 2k \end{array}\right.$

  (3) 최빈값(mode)

  • 관측치 중에서 가장 많이 관측되는 값

  • 옷사이즈와 같이 명목형 데이터의 경우 사용

    

3 ) 산포도

• 데이터가 어떻게 흩어져 있는지를 확인하기 위해서는 중심경향치와 함께 산포에 대한 측도를 같이 고려해야 함

• 데이터의 산포도를 나타내는 측도로는 범위, 사분위수, 분산, 표준편차, 변동 계수 등이 있음

  (1) 범위(Range)

  • 데이터의 최대값과 최소값의 차이를 의미함

  (2) 사분위수(quartile)

  • 전체 데이터를 오름차순으로 정렬하여 4등분을 하였을 때, 첫 번째를 제1사분위수(Q1), 두 번째를 제2사분위수(Q2), 세 번째를 제3사분위수(Q3)이라고 함
  • 사분위수 범위(interquartile range)
    IQR = 제 3사분위수(Q3) – 제1사분위수(Q1)

  (3) 백분위수(percentile)

  • 전체 데이터를 오름차순으로 정렬하여 주어진 비율에 의해 등분한 값을 말하며, 제p백분위수는 p%에 위치한 자료 값을 말함
  • 데이터를 오름차수로 배열하고 자료가 n개가 있을 때, 제(100*p) 백분위수는 아래와 같음
    1) np가 정수이면, np번째와 (np + 1)번째 자료의 평균
    2) np가 정수가 아니면, np보다 큰 최소의 정수를 m이라고 할 때 m번째 자료

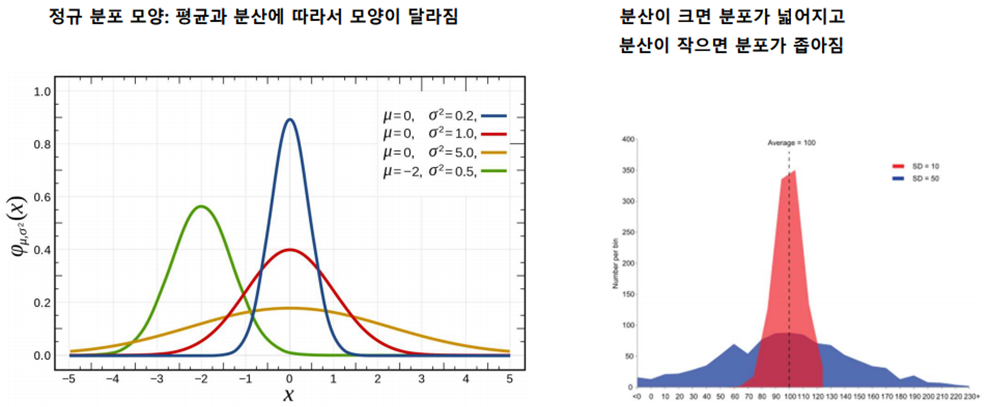
  (4) 분산(variance)

  • 데이터의 분포가 얼마나 흩어져 있는지를 알 수 있는 측도 임

  • 데이터의 각각의 값들의 편차 제곱합으로 계산하며 수식은 아래와 같음

    표본 분산 : $s^2 = \frac{1}{n-1} \sum_{i=1}^{n} (x_i - \bar{x})^2$

  

  (5) 표준 편차(standard deviation)

  • 분산의 제곱근으로 정의하며 수식은 아래와 같음
    표본 표준 편차 : $s = \sqrt{s^2}$

  (6) 모분산 / 모표준편차

  • 크기가 n인 모집단의 평균을 $\mu$ 라고 할 때 모평균과 모분산은 다음과 같음
    모분산 : $\sigma^2 = {\frac{1}{n} \sum_{i=1}^{n} (x_i - \mu)^2}$

    모표준편차 : $\sigma = \sqrt{\sigma^2}$

  (7) 변동계수(Coefficient of Variation: CV)

  • 평균이 다른 두개 이상의 그룹의 표준편차를 비교할 때 사용함
  • 변동계수는 표준편차를 평균으로 나누어서 산출하여 단위나 조건에 상관 없이 서로 다른 그룹의 산포를 비교하며 실제 분석에서 자주 사용함
    $cv = \frac{s}{\bar{x}}$

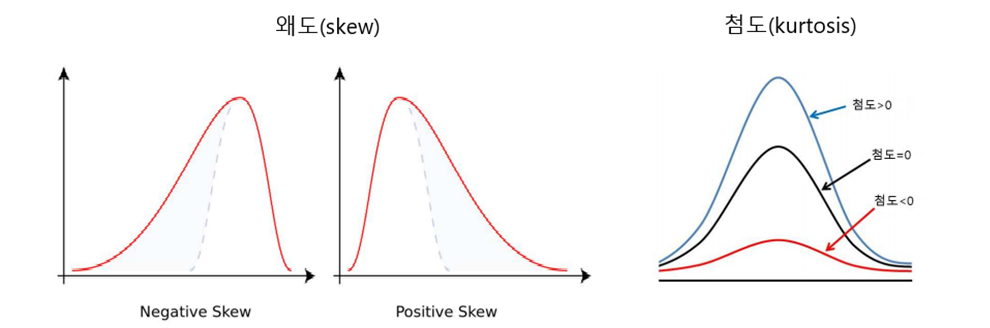
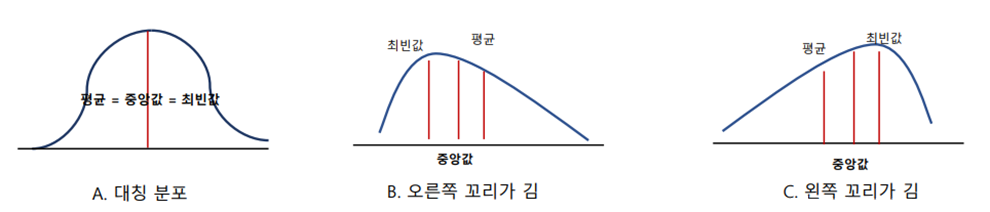
  (8) 왜도(skew)

  • 자료의 분포가 얼마나 비대칭적인지 표현하는 지표임
  • 왜도가 0이면 좌우가 대칭이고, 0에서 클수록 우측꼬리가 길고 0에서 작을수록 좌측 꼬리가 김

  (9) 첨도(kurtosis)

  • 확률분포의 꼬리가 두꺼운 정도를 나타내는 척도임
  • 첨도값(K)이 3에 가까우면 산포도가 정규분포에 가까움
  • 첨도값이 3보다 작을 경우에는(K<3) 산포는 정규분포보다 꼬리가 얇은 분포로 판단
  • 첨도값이 3보다 큰 양수이면(K>3) 정규분포보다 꼬리가 두꺼운 분포로 판단