1. 확률
1) 확률의 정의
확률 (probability)
모든 경우의 수에 대한 특정 사건이 발생하는 비율이다. 대체로 수학 외에서는, 0과 1 사이의 소수 혹은 분수나 순열 등으로 나타내기보다는, 다른 비율을 나타낼 때처럼 0과 1 사이의 확률에 100을 곱하여 0과 100 사이의 백분율(%)로 나타내거나 옛날처럼 할·푼·리로 나타내기도 한다. (출처: 나무위키)
확률의 고전적 정의
어떤 사건의 발생 확률은 그것이 일어날 수 있는 경우의 수 대 가능한 모든 경우의 수의 비이다. 단, 이는 어떠한 사건도 다른 사건들보다 더 많이 일어날 수 있다고 기대할 근거가 없을 때, 그러니까 모든 사건이 동일하게 일어날 수 있다고 할 때에 성립한다. (확률의 최초의 정의는 수학자 라플라스의 논문 Théorie analytique des probabilités)
표본 공간(Sample Space)
표본 공간이란 어떤 실험에서 나올 수 있는 모든 가능한 결과들의 집합
동전 던지기의 경우 S = {앞면, 뒷면} , 주사위던지기 S = {1,2,3,4,5,6}
사건 A가 일어날 확률을 P(A)라고 하고, 표본 공간(S)가 유한집합일때 표본 공간의 모든 원소들이 일어날 확률이 같으면
P(A)=표본공간S의원소의수사건A가일어날원소의수
통계적 확률 정의
어떤 시행을 N번 반복했을 때, 사건 A에 해당하는 결과가 r번 일어난 경우 Nr이고, 사건 A가 일어날 상대도수라고 함
N이 무한히 커지면 상대도수는 일정한 수로 수렴하는데, 이 극한값을 limN→∞Nr 을 사건 A의 통계적 확률 또는 경험적 확률 이라고 함
2) 확률의 성질
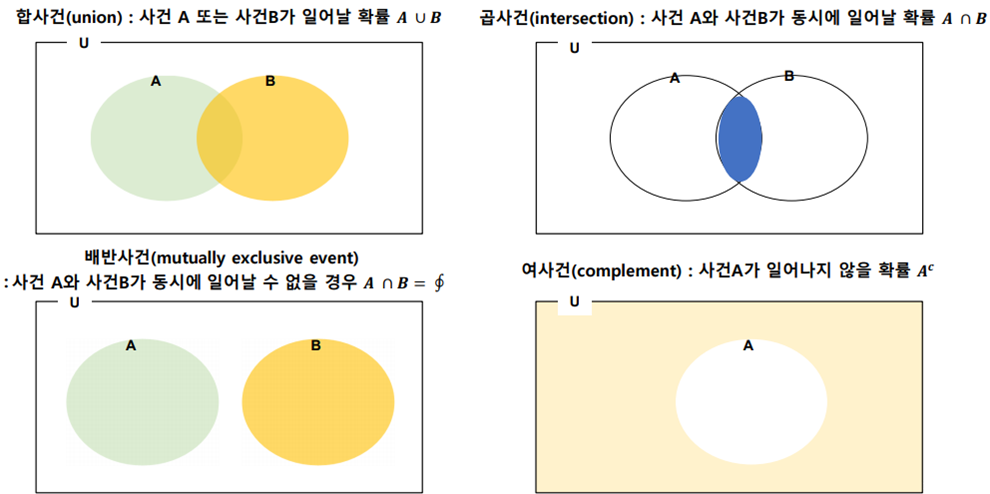
- 확률의 덧셈법칙 : P(A∪B)=P(A)+P(B)−P(A∩B)
- A와 B가 배반 사건이면 P(A∩B)=P(∮)=0
- A의 여사건이 Ac 이면 P(A)+P(Ac)=1
조합과 순열
-
! (Factorial): n개를 일렬로 늘여 놓은 경우의 수를 n!로 표현
n!=n⋅(n−1)⋅(n−2)…2⋅1
-
순열(Permutation): 순서를 고려하여 n개 중 r개를 뽑아서 배열하는 경우의 수
nPr=(n−r)!n!
-
조합(Combination) : 순서를 고려하지 않고 n개중 r개를 뽑아서 배열하는 경우의 수
nCr=(rn)=r!(n−r)!n!
조건부 확률
-
조건부 확률(conditional probability) : 어떤 사건 A가 발생한 상황에서(주어졌을 때) 또 하나의 사건 B가 발생할 확률
P(B∣A)=P(A)P(A∩B),P(A)=0
P(A∣B)=P(B)P(A∩B),P(B)=0
-
확률의 곱셈법칙
P(A∩B)=P(A)⋅P(B∣A)=P(B)⋅P(A∣B)
사건 A와 B가 독립일 경우, P(A∩B)=P(A)⋅P(B)
-
베이즈 정리(Bayes’ Theorem) : 표본 공간 S에서 서로 배반인 사건 B1,B2,…,Bk 에 의하여 분할 되어 있을때, 임의의 사건 A에 대하여 다음이 성림
P(Bi∣A)=P(A)P(Bi∩A)=∑j=1kP(A∣Bj)⋅P(Bj)P(A∣Bi)⋅P(Bi)
2. 확률 변수
확률 변수(random variable)
-
표본공간에서 각 사건에 실수를 대응시키는 함수를 확률 변수라고 함
-
확률 변수의 값은 하나의 사건에 대하여 하나의 값을 가지며, 실험의 결과에 의하여 변함
-
일반적으로 확률 변수는 대문자로 표현하며, 확률변수의 특정값을 소문자로 표현함
- 확률 변수: X, Y 등 대문자 표현
- 확률 변수의 특정값: x, y등 소문자로 표현
- 이산 확률 변수(discrete random variable): 셀 수 있는 값들로 구성되거나 일정 범위로 나타나는 경우
- 연속 확률 변수(continuous random variable): 연속형 또는 무한대와 같이 셀 수 없는 경우
- 확률 변수 예시
(a) 반도체 1000개의 wafer중 불량품의 수 X
(b) 공장에서 생산하는 전구의 수명 T
(c) 주사위를 던질 때 나오는 눈의 수 V
-
확률 변수의 평균 : 기대값 이라고 표현하기도 하며, 수식은 아래와 같음
E(X)=∑i=1n xiP(xi)=x1P(x1)+x2P(x2)+⋯+xnP(xn)
-
확률 변수의 분산
var(x)=N1∑(xi−μ)2
기대값의 성질
a, b가 상수이고, X, Y를 임의의 확률 변수라고 할 때 다음이 성립한다.
- E(a)=a
- E(aX)=aE(X)
- E(aX+b)=aE(X)+b
- E(aX±bY)=aE(X)±bE(Y)
- X,Y가독립일때E(XY)=E(X)⋅E(Y)
분산의 성질
a, b가 상수이고, X, Y를 임의의 확률 변수라고 할 때 다음이 성립한다.
- Var(a)=0
- Var(aX)=a2Var(X)
- Var(X+Y)=Var(X)+Var(Y)+2cov(X,Y)
- Var(aX±bY)=a2Var(X)±b2Var(Y)+2Cov(X,Y)
- X,Y가독립일때 Var(XY)=0
- Var(X)=E(X2)−[E(X)]2
공분산
2개의 확률변수의 선형 관계를 나타내는 값으로, 하나의 값이 상승할 때 다른 값도 상승한다면, 양의 공분산을 가지고
반대로 하나의 값이 상승할 때 하락한다면 음의 공분산을 가짐
- cov(X,Y)=E[(X−E(X))(Y−E(Y))]=n−1∑in(Xi−Xˉ)(Yi−Yˉ)