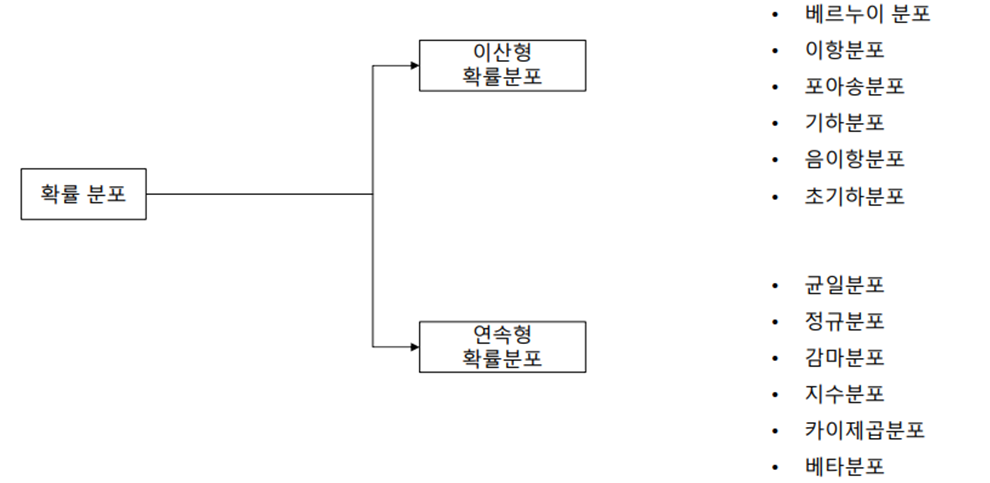
1. 이산형 확률 분포
확률 분포(probability distribution)
확률 변수 X가 취할 수 있는 모든 값과 그 값을 나타날 확률을 표현한 함수
(1) 이산형 균등 분포(discrete uniform distribution)
-
확률 변수 X가 유한개이고, 모든 확률 변수에 대하여 균일한 확률을 갖는 분포를 이산형 균등 분포라고 함
-
-
-
(2) 베르누이 분포(Bernoulli distribution)
-
베르누이 시행(Bernoulli trial): 각 시행의 결과가 성공, 실패 두가지 결과만 존재하는 시행
-
베르누이 시행에서 성공이 ‘1’, 실패가 ‘0’의 값을 갖을 때 확률 변수 X의 분포를 베르누이 분포라고 하며 다음과 같이 정의함
-
-
-
(3) 이항분포(Binomial distribution)
-
연속적인 베르누이 시행을 거처 나타나는 확률 분포
-
서로 독립인 베르누이 시행을 n번 반복해서 실행 했을 때, 성공한 횟수 X의 확률 분포
-
-
-
-
(4) 포아송 분포(Poisson distribution)
-
어느 희귀한 사건이 어떤 일정한 시간대에 특정한 사건이 발생할 확률 분포
-
포아송 분포의 조건
- 어떤 단위구간(예, 1일)동안 이를 더 짧은 작은 단위의 구간(예: 1시간)로 나눌 수 있고 이러한 더 짧은 단위구간 중에 어떤 사건이 발생할 확률은 전체 척도 중에서 항상 일정
- 두 개 이상의 사건이 동시에 발생할 확률은 0에 가까움
- 어떤 단위구간의 사건의 발생은 다른 단위구간의 발생으로부터 독립적임
- 특정 구간에서의 사건 발생확률은 그 구간의 크기에 비례함
- 포아송분포 확률 변수의 기댓값과 분산은 모두 λ 임
-
-
이항 분포의 포아송 근사
확률 변수 X가 이고, n이 충분히 크고, p가 아주 작을 때, X의 분포는 평균이 인 포아송 분포로 근사 시킬 수 있음
보통 n이 클때, np<5를 만족하게 p가 작으면 근사 정도가 좋다고 함 X ~ Poisson(np)
(5) 기하 분포(geometric distribution)
-
어떤 실험에서 처음 성공이 발생하기 까지 시도한 횟수 X의 분포, 이때 각 시도는 베르누이 시행을 따름
-
-
-
(6) 음이항분포(negative binomial distribution)
-
어떤 실험에서 성공확률이 p일 때, r번의 실패가 나올 때 까지 발생한 성공 횟수 X의 확률 분포
-
-
-
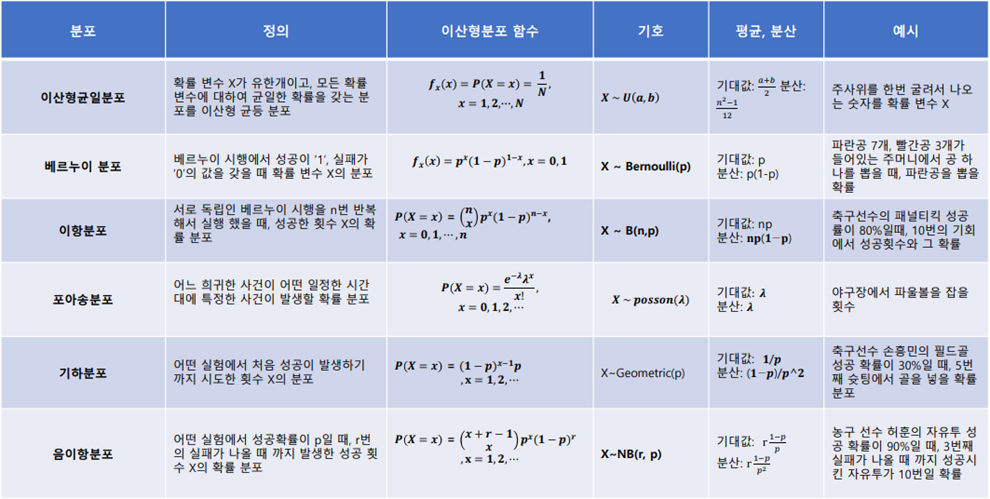
이산형 확률 분포 – summary
2. 연속형 확률 분포
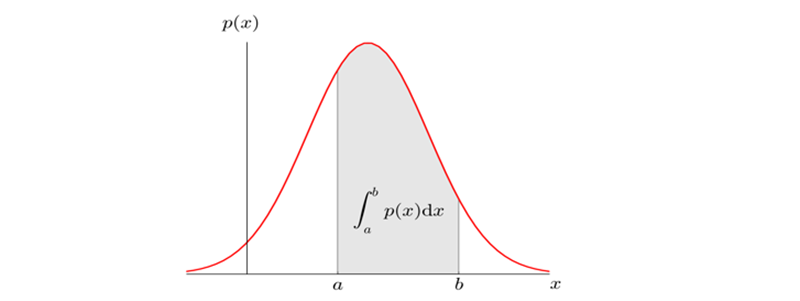
(1) 확률 밀도 함수(probability density function)
-
연속형 확률 변수 X에 대해서 함수 가 특정 조건을 만족하면 확률밀도함수라고 함
-
확률 밀도 함수 조건
-
모든 X에 대해서
-
-
-
-
확률 밀도 함수의 성질
-
-
확률 밀도 함수의 평균과 분산
-
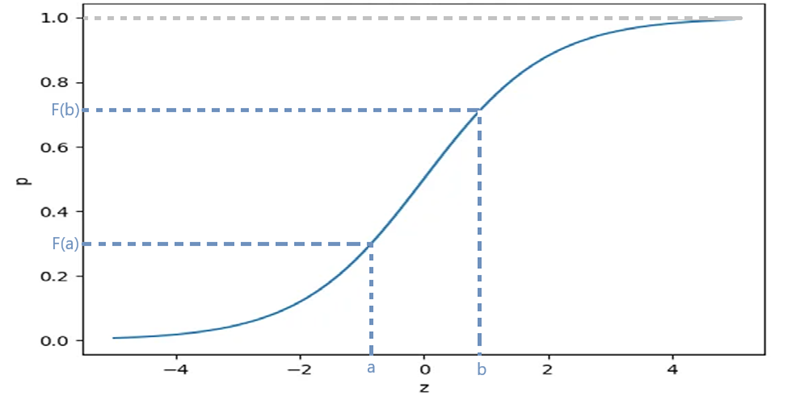
(2) 누적 분포 함수(cumulative density function)
-
확률 밀도 함수를 적분하면 누적 분포 함수가 됨
-
-
누적분포함수의 성질
-
-
만약
-
-
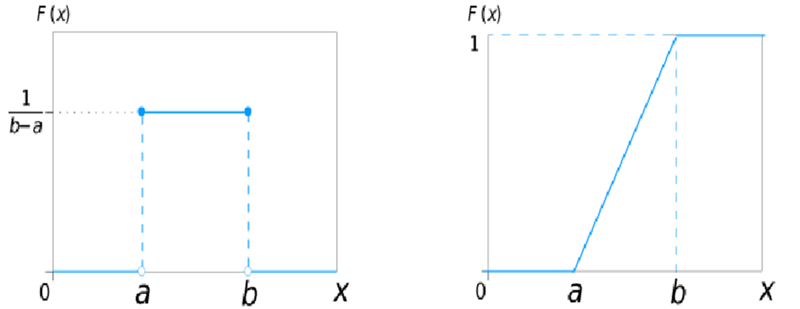
(3) 균일 분포(uniform distribution)
-
확률 변수 X가 a와 b사이에서 아래와 같은 확률 밀도 함수(pdf)를 가짐
-
PDF
-
CDF :
-
-
-
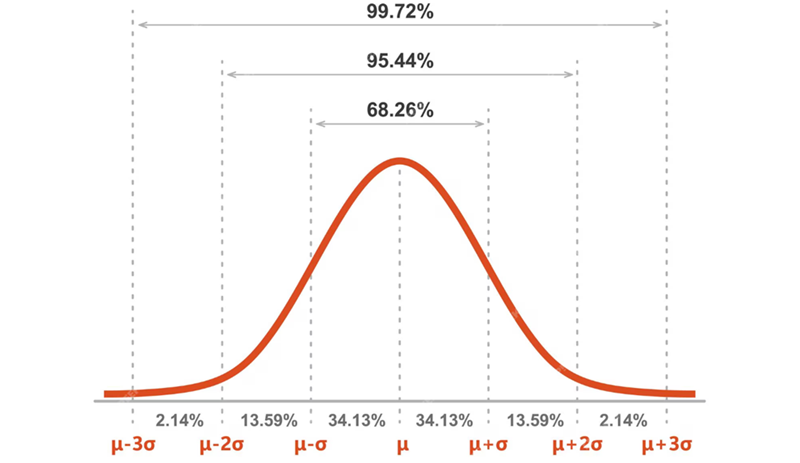
(4) 정규 분포(normal distribution)
-
정규 분포는 19세기 최대 수학자라고 불리는 독일의 가우스에 의해 제시된 것으로 가우스 분포라고도 함
-
확률 밀도 함수는 확률 변수 가 평균이 이고, 분산이 인 정규분포를 따를 때 아래와 같음
-
-
정규 분포(normal distribution)의 평균과 분산
-
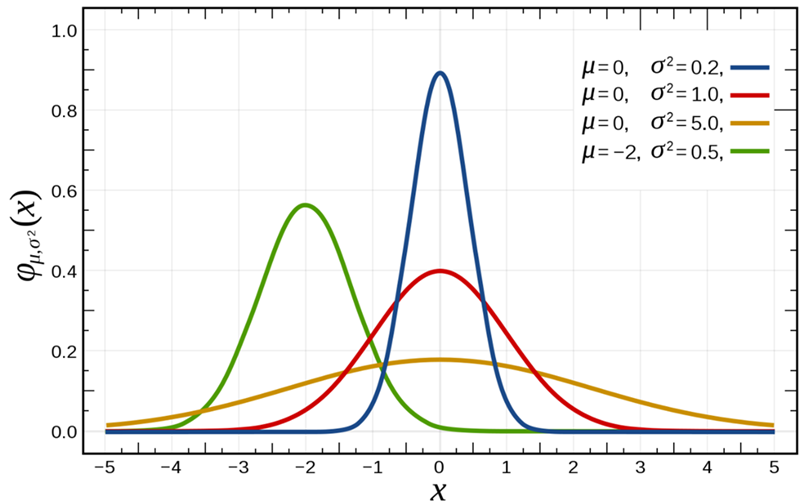
파라메터의 따른 정규 분포 모양 비교
-
표준 정규 분포(standard normal distribution)
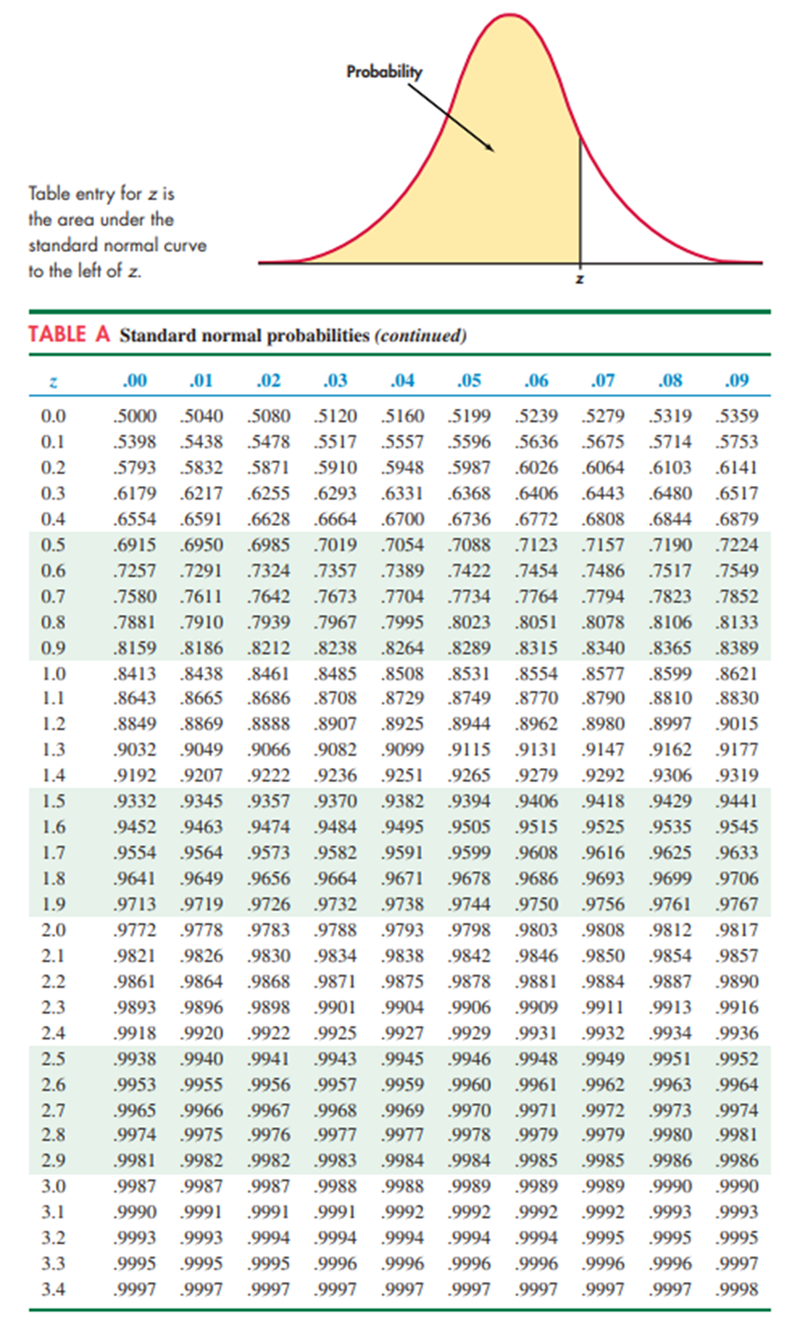
-
정규 분포의 성질
-
일때, 임수의 상수 a, b에 대하여
-
일때,
-
이고 X와 Y가 독립일때,
-
-
이항분포의 정규 근사
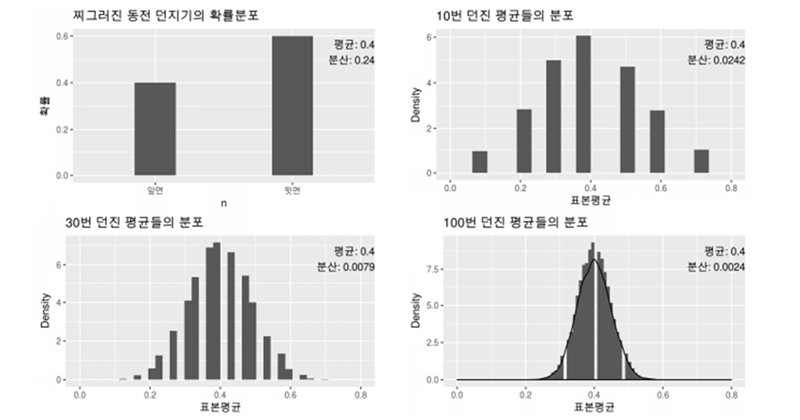
- 일때 확률 변수 X는 n이 충분히 크면 근사적으로 정규 분포 를 따름
- 일때 확률 변수 X는 n이 충분히 크면 근사적으로 정규 분포 를 따름
(5) 지수분포(exponential distribution)
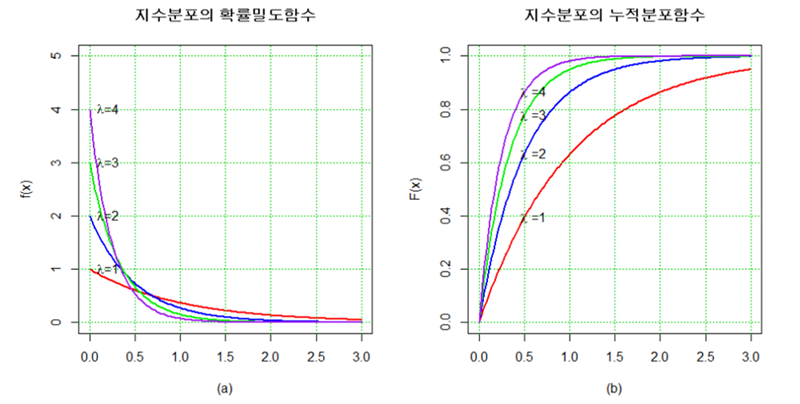
-
단위 시간당 발생할 확률 인 어떤 사건의 횟수가 포아송 분포를 따르다면, 어떤 사건이 처음 발생 할때까지 걸린 시간 확률 변수 X는 지수 분포임
-
PDF
-
CDF
-
-
-
지수분포의 무기억성 (Memoryless Property) : 어떤 시점 부터 소요되는 시간은 과거 시간에 영향을 받지 않음
-
지수분포와 포아송 분포의 관계
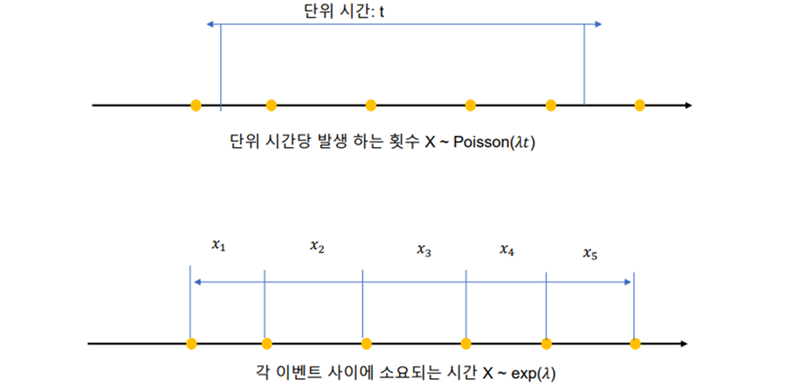
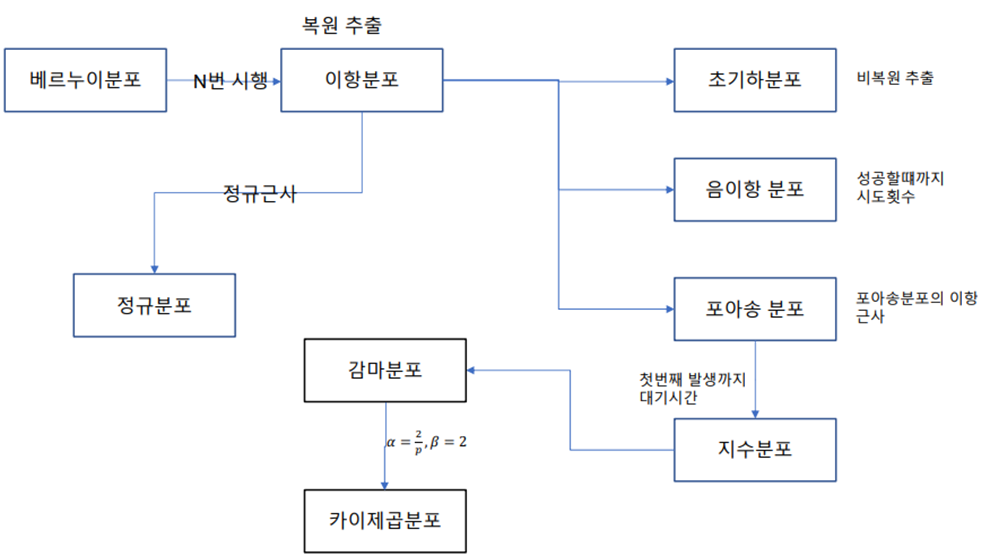
연속형 확률 분포 – 확률 분포의 관계도