최단경로
-
그래프는 지도에서 도시를 나타내는 점과 그들 도시 간의 거리를 나타내는 연결선의 값(거리)으로 표현됨
-
도시 A에서 도시 B로 가는 방법
1) A에서 B로 가는 경로가 있느냐는 점
2) A에서 B로 가는 경로가 여러개 있을 경우 어떤 경로로 가는 것이 가장 짧은 거리인가 하는 점 -
가장 짧은 거리의 경로를 찾는 문제를 최단경로 문제라 함.
-
주어진 방향그래프에서 경로의 시작점을 출발점(Source)이라 하며 목적지를 도착점이라고 한다
-
주어진 연결선의 길이는 0 이상인 경우를 가정함
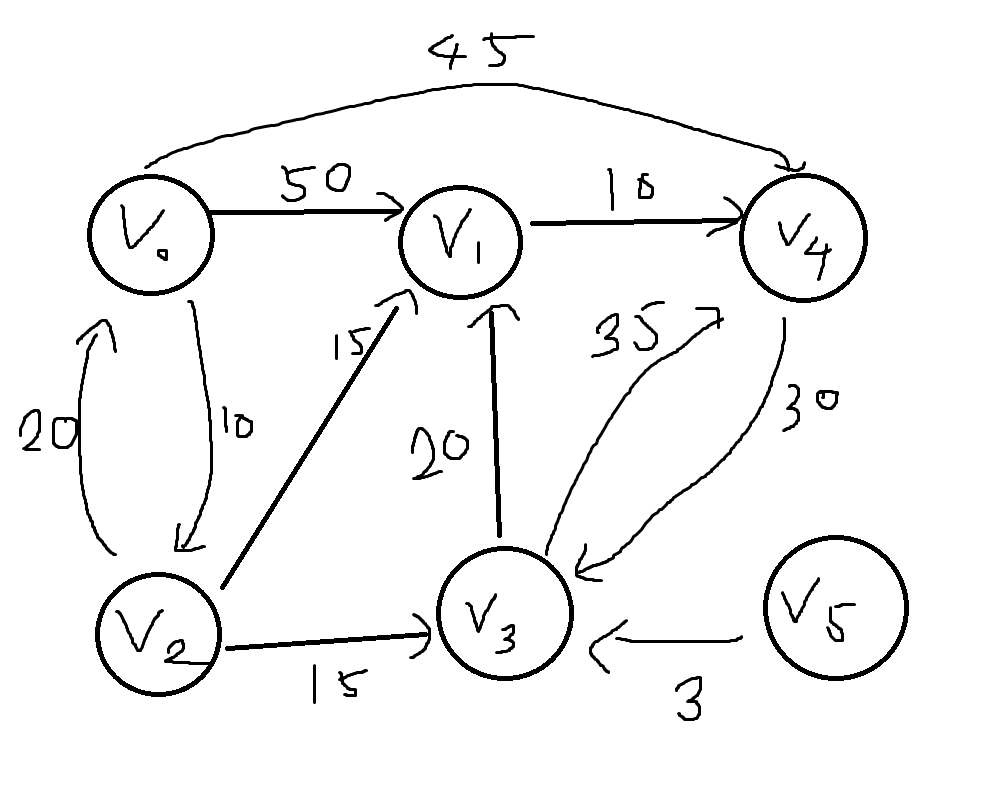
- 연결선의 값이 두점 사이의 거리를 나타낼 때, V0가 출발점이라 하면 V0에서 V₁까지의 최단경로는 V0 V2 V3 V1임
- 이때 최단거리는 10+15+20 = 45가 됨
- 경로의 길이는 3이지만 V0에서 V1로 바로가는 거리인 50보다 짧음
- V0에서 V1,V2,V3,V4로 가는 최단경로의 값을 나타냄
| 경로 | 거리 | |
|---|---|---|
| 1 | V0 V2 V3 V1 | 45 |
| 2 | V0 V2 | 10 |
| 3 | V0 V2 V3 | 25 |
| 4 | V0 V4 | 45 |
-
최단경로의 거리문제를 해결할 수 있는 방법을 다익스트라 알고리즘(Diikstra algorithm)이라고 함
-
출발점으로부터 거리가 최소로 알려진 점들의 집합 S를 유지함으로써 가장 짧은 거리를 가지는 나머지 점 V를 차례로 S에 포함시킴
다익스트라 알고리즘
-
주어진 방향그래프 G = (V, E)에서 v = (1,2,...,n)이고 점 {1}이 출발점이라고 가정함
-
점 i에서 j로 가는 거리를 C|i,j|로 나타내는데, 만약 i에서 j로 가는 경로가 없으면 거리는 ∞가 됨
-
D[i]는 출발점에서 현재점 i에 이르는 가장 짧은 거리를 나타냄
-
다익스트라 알고리즘
void Diikstra()
{
S = {1};
for (i = 2; i<=n; i++)
D[i] = C[1,f];
for (i=1, i<=n-1; i++)
{
choose a vertex in V-S such that D[w] is a minimum;
add w to S;
for (each vertex v in V-S)
D[v] = min(D[v], D[w] C[w,v];
}}
S = 경로저장. W = 현재의 거리 중에 제일 짧은 것(정점)
- 방법 설명
1) 시작점을 기준으로 다른 정점으로 연결된 거리를 표에 입력. 바로가는 방법이 없으면 ∞를 입력
2) 가장 짧은 거리로 가는 정점을 S와 W에 추가하고 해당 D[n]은 그 거리로 고정(비교에서 제외)
3) 해당 정점에서 연결되는 점이 있는지 판단하고 있으면 사작점에서 해당 점으로 가는 가장 빠른 거리 계산, 기존 거리와 비교
4) 반복
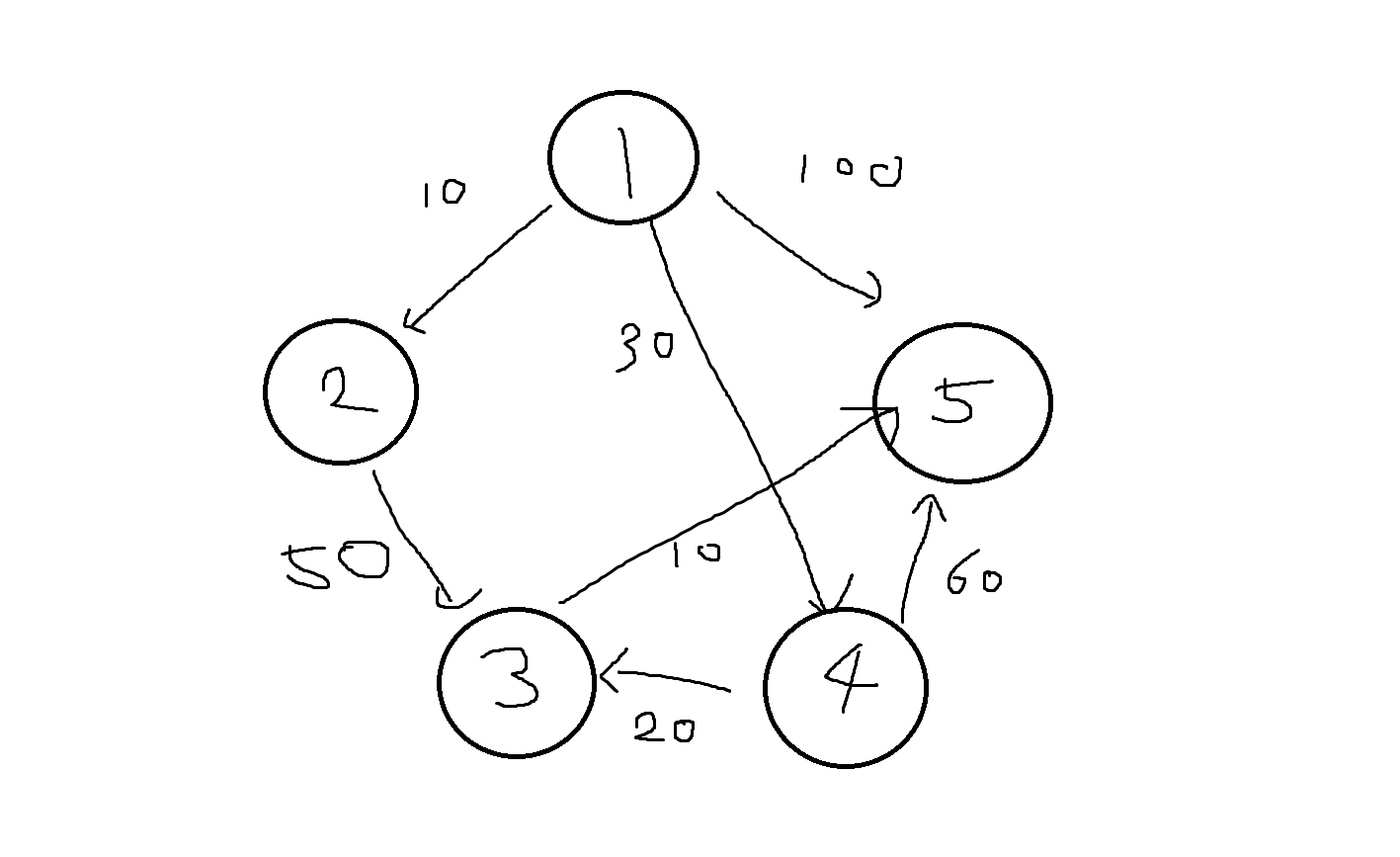
| S | W | D[2] | D[3] | D[4] | D[5] |
|---|---|---|---|---|---|
| {1} | - | 10 | ∞ | 30 | 100 |
| {1,2} | 2 | 10 | 60 | 30 | 100 |
| {1,2,4} | 4 | 10 | 50 | 30 | 90 |
| {1,2,4,3} | 3 | 10 | 50 | 30 | 70 |
| {1,2,4,3,5} | 5 | 10 | 50 | 30 | 70 |
- 표 설명
1) 시작점 1
2) 1에서 가는 가장 짧은 점 2를 S와 W에 추가 (D[2]는 고정)
3) 2에서 3으로 가는 방법 존재, 가장 짧은거리 60. (60<∞이므로 60으로 변경)
2에서 4로 가는 방법 없음. 즉 ∞. (30 < ∞)이므로 30 유지
2에서 5로 가는 방법도 같은 이유로 100으로 유지
4) 1과 2를 제외하고 가장 짧은점 4를 S와 W에 추가 (D[4] 고정)
5) 4에서 3으로 가는점 존재 (50<60)이므로 50으로 대체
4에서 5로 가는점 존재 (90<100)이므로 90으로 대체
6) 1,2,4를 제외하고 가장 짧은 점 3을 S와 W에 추가 (D[3] 고정)
7) 3에서 5로 가는점 존재. (70<90)이므로 70으로 대체.
8) 마지막 남은점 5를 S와 W에 추가.
9) 결론. 최단거리는 1 - 2 - 4 - 3 - 5
연습문제
1) 3차 정규그래프의 예를 만들어보시오
3차 정규그래프 = 모든 꼭지점의 차수가 3
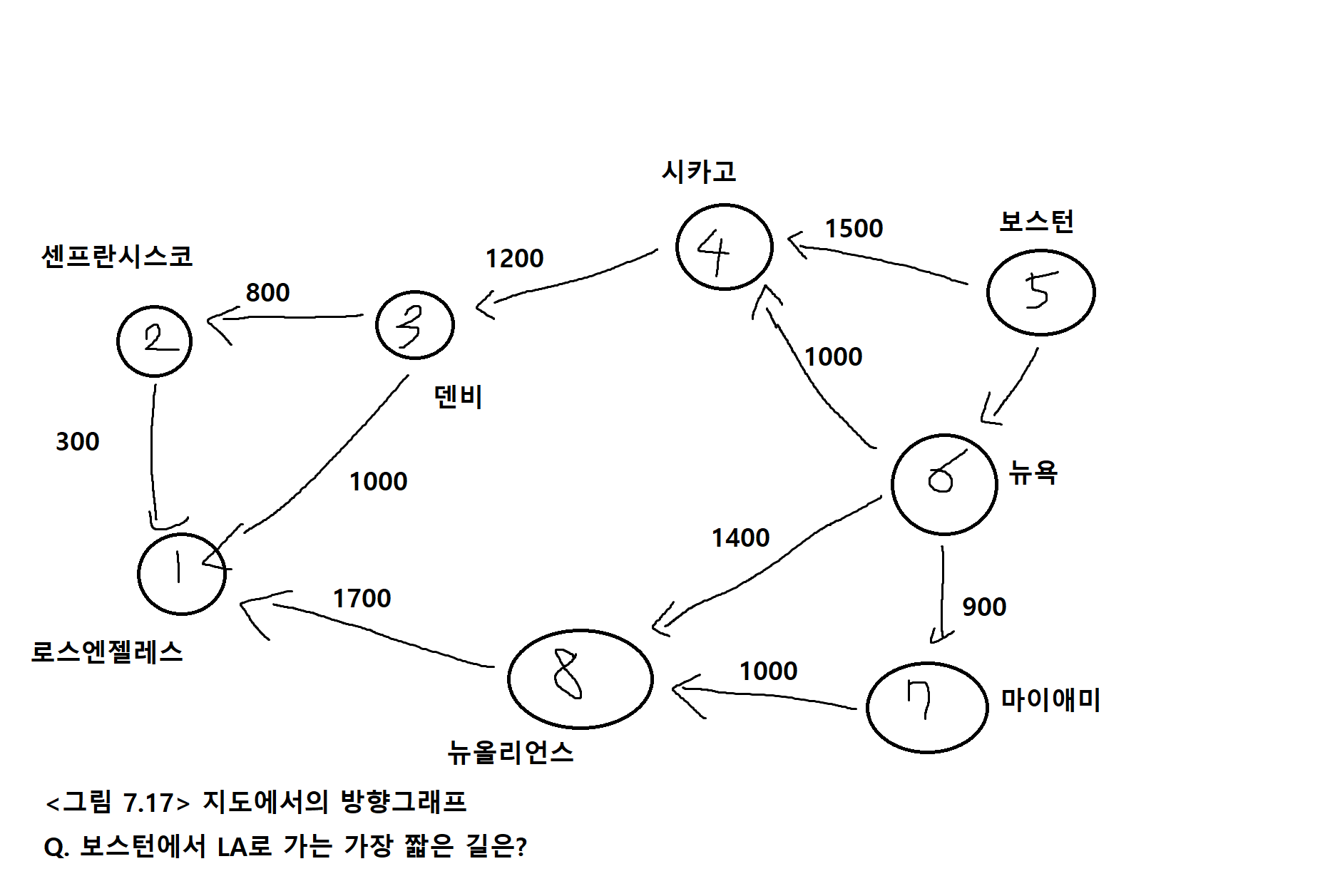
2) 다음 방향그래프의 1번 정점에서 다익스트라 알고리즘을 이용하여 다른 모든 정점으로 가는 최단거리를 구하시오
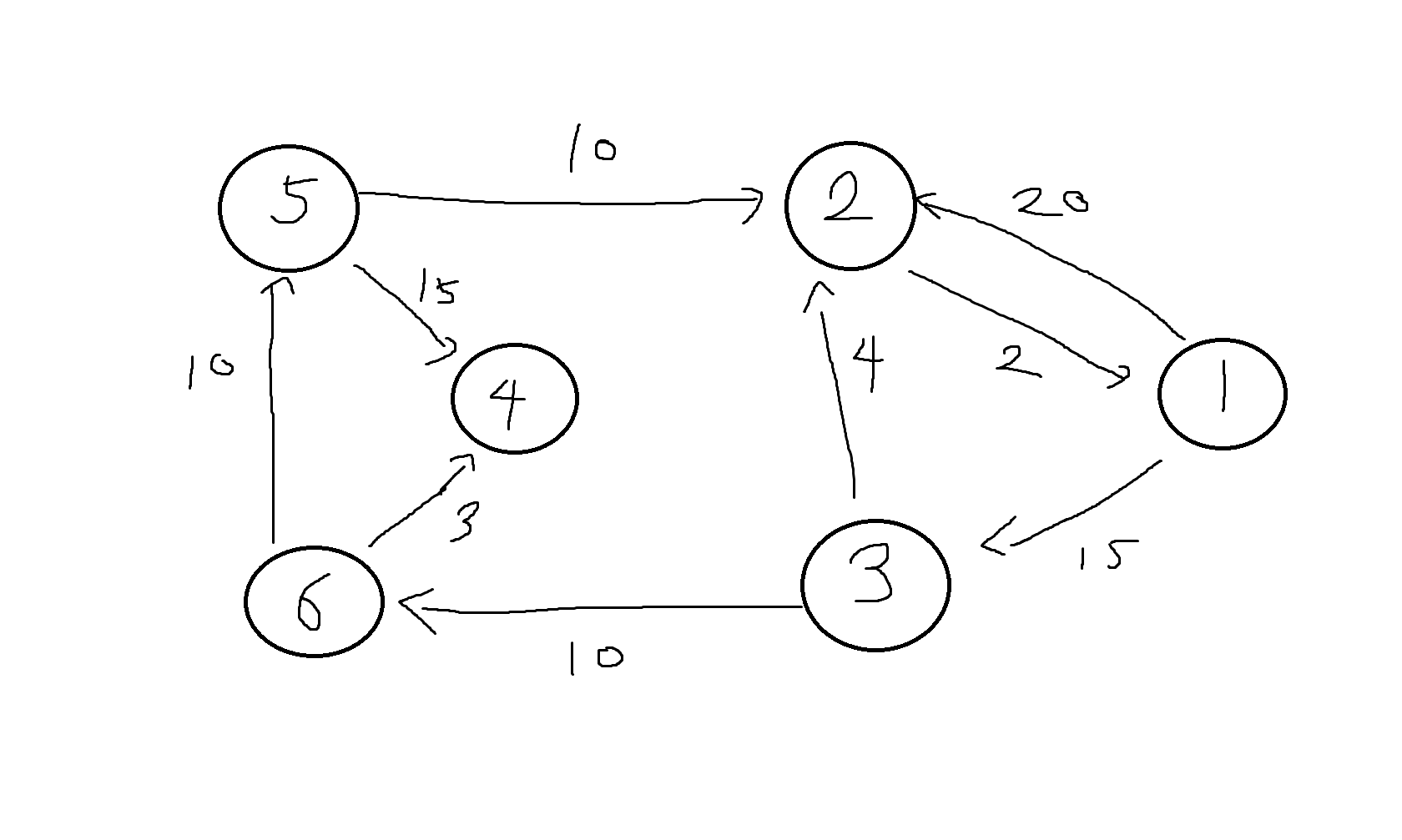
| S | W | D[2] | D[3] | D[4] | D[5] | D[6] |
|---|---|---|---|---|---|---|
| {1} | - | 20 | 15 | ∞ | ∞ | ∞ |
| {1,3} | 3 | 19 | 15 | ∞ | ∞ | 25 |
| {1,3,2} | 2 | 19 | 15 | ∞ | ∞ | 25 |
| {1,3,2,6} | 6 | 19 | 15 | 28 | 35 | 25 |
| {1,3,2,6,4} | 4 | 19 | 15 | 28 | 35 | 25 |
| {1,3,2,6,4,5} | 5 | 19 | 15 | 28 | 35 | 25 |
- 풀이 설명
1) 시작점 1, 1에서 2로 가는 경로 존재(D[2] = 20), 1에서 3으로 가는점 존재(D[3]=15), 1에서 4, 5, 6으로 가는 경로 없음 (∞로 설정)
2) 1을 제외한 최단거리 정점은 3, 3을 S와 W에 추가 (D[3]값 고정),
3에서 2로 가는 경로 존재, (19<20)이므로 D[2]를 19로 변경.
3에서 6으로 가는 경로 존재, (25<∞)이므로 D[6]을 25로 변경
3에서 4와 5로가는 경로는 존재 X (∞ 유지)
3) 1,3을 제외한 최단거리 정점 2를 S와 W에 추가 (D[2]값 고정)
2에서 4, 5로가는 경로 존재 X, ∞유지
2에서 6으로 가는 경로 존재, (25<49)이므로 25유지
4) 1,3,2를 제외한 최단거리 정점 6을 S와 W에 추가 (D[6]값 고정)
6에서 4로가는 경로 존재, (28<∞)이므로 D[4]를 28로 교체
6에서 5로가는 경로 존재, (35<∞)이므로 D[5]를 35로 교체
5) 1,3,2,6을 제외한 최단거리 점 4를 S와 W에 추가 (D[4]값 고정)
4에서 5로 가는 경로 존재 X, (35<∞)이므로 35유지
6) 마지막 남은 정점인 5를 S에 추가
따라서 최단거리는 {1,3,2,6,4,5}가 된다.
(2) 해밀턴 순회의 응용
-> 순회판매원문제 (모든 도시를 한번씩만 방문, 여행거리가 최소가 되는 경로를 찾는 문제, 최소의 경로가 '최적'의 경로라고 할 수 있음. 일반적인 해결 알고리즘이 존재하지 않음. NP(Ncondeterministic Polynomial) - comple: 다항식 알고리즘으로 풀 수 없는 문제.
-
최근접 이웃방법을 통하여 최소값은 아니더라도 근사값은 구할 수 있음
(일종의 greedy한 방법인 것) -
임의로 선택한 꼭지점에서 출발하여 그 꼭지점과 가장 가까운 꼭지점을 찾아서 연결
-
경로를 참가하는 과정을 반복하여 마지막에 순회를 형성하도록 하는 것임
begin
choose any V1(시작점) ∈ V
V' <- V1 (시작점 할당)
W <- 0
Add V' to the first of Vertices in the path (경로에 V'에 저장된 값 입력)
While unmarked vertices are remained do
begin
Mark V',
Choose any unsigned vertex, that is closest to V'
Add u to the list of Vertices in the path
W <- W+ the weight of edge (V', u)
V' <- u
end
Add V' to the list of Vertices in the path
W <- W+ the weight of the edge (V', V1)
end
예제 7-15. 다음의 가중그래프에서 최근점 이웃방법을 적용한 해밀턴 순회를 만들어보자.
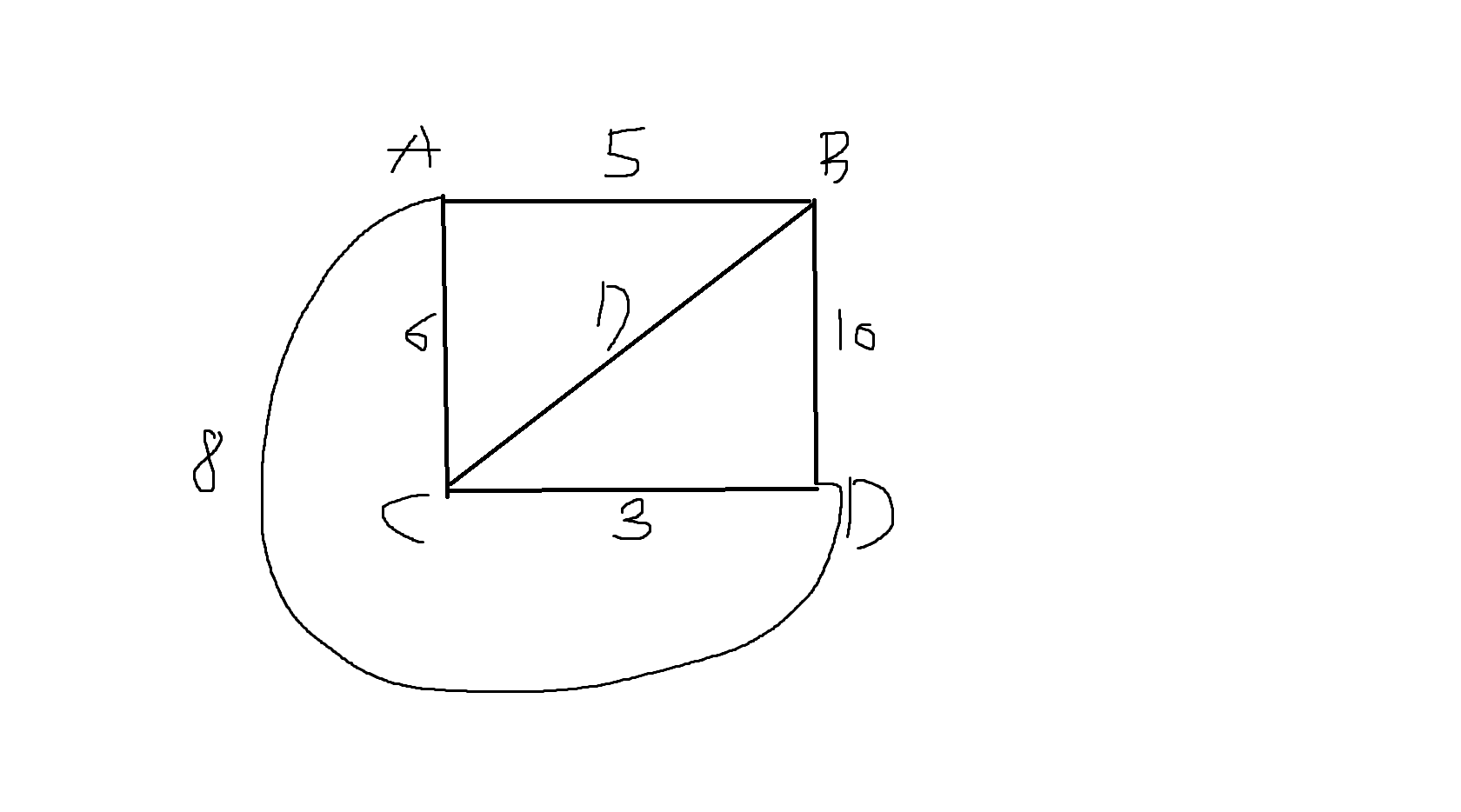
B에서 시작
B - A - C - D - B
W = 0 + 5 + 6 + 3 + 10 = 24 (최적) <- 최소인가? -> No (B A D C B = 0 + 5 + 8 + 3 + 7 = 23으로 최소)
-> 도시가 수십만개면 이렇게 눈으로 파악하기 힘들다. 그래서 근접한 최적값을 구하는 것
(1) 길이 우선탐색 (Depth First Search : DFS)
-
깊이 우선 탐색은 시작점 v부터 방문함
-
v에 인접한 정점 중에서 방문하지 않은 정점 w를 방문하고 다시 w로부터 탐색을 시작함
-
어떤 정점 u를 방문하고 u에 인접한 모든 정점들을 이미 방문한 경우 그전에 마지막으로 방문한 정점으로 되돌아가서 위의 과정을 반복함
-
모든 정점들을 방문 후 탐색종료
-> 순차적인 프로그램보다는 DFS알고리즘을 재귀적(recursive) 알고리즘으로 구현하는 것이 좋음
-> 재귀적 알고리즘으로 구현할 경우에는 스택(Stack)을 사용함
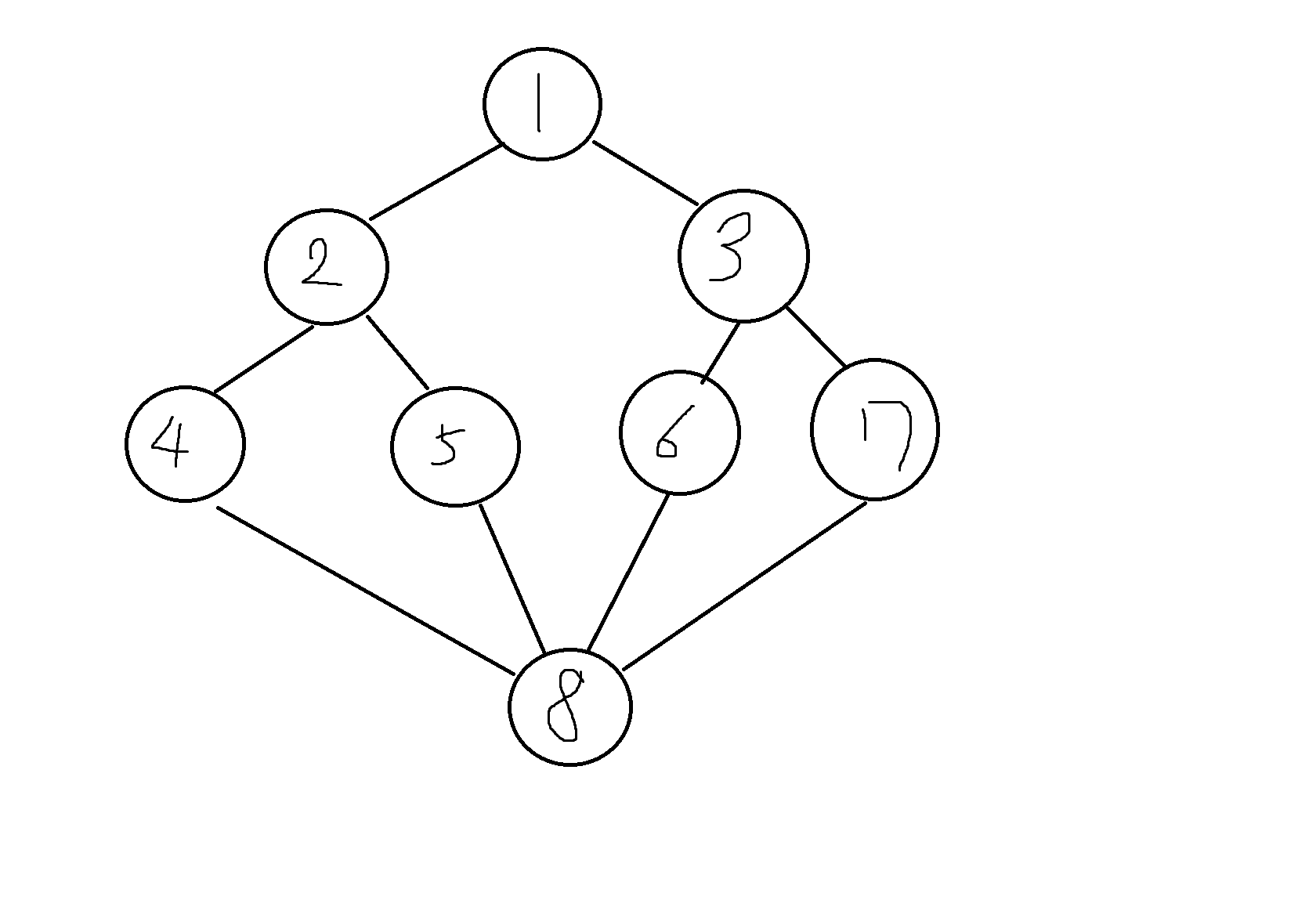
1부터 시작하고 작은 번호부터 탐색한다고 가정할 때, DFS의 탐색결과는?
1 - 2 - 4 - 8 - 5 - 6 - 3 - 7
(2) 너비우선 탐색 (Breadth First Search : BFS)
-
너비우선탐색은 처음에 방문한 정점과 인접한 정점들을 차례로 방문한다는 점에서 깊이우선탐색과 차이가 있음
-
먼저 시작점 V를 방문한 후 V에 인접한 모든 정점들을 차례로 방문함.
-
더 이상 방문할 정점이 없는 경우 다시 V에서 인접한 정점들 가운데 맨 처음으로 방문한 정점과 인접한 정점들을 차례로 방문함
-
V에 인접한 정점 중 두번째로 방문한 정점과 인접한 정점들을 차례로 방문하는 과정을 반복
-
모든 정점들을 방문한 후 탐색을 종료함
-> 깊이우선탐색이 스택(Stack)을 사용하는데 비해 너비우선탐색은 큐(Queue)를 사용
// DFS
void dfs(int v)
{
int w;
visted[v] = True;
for (each vertex w adjacent to v)
if (vistied[w]))
dfs(w);
}
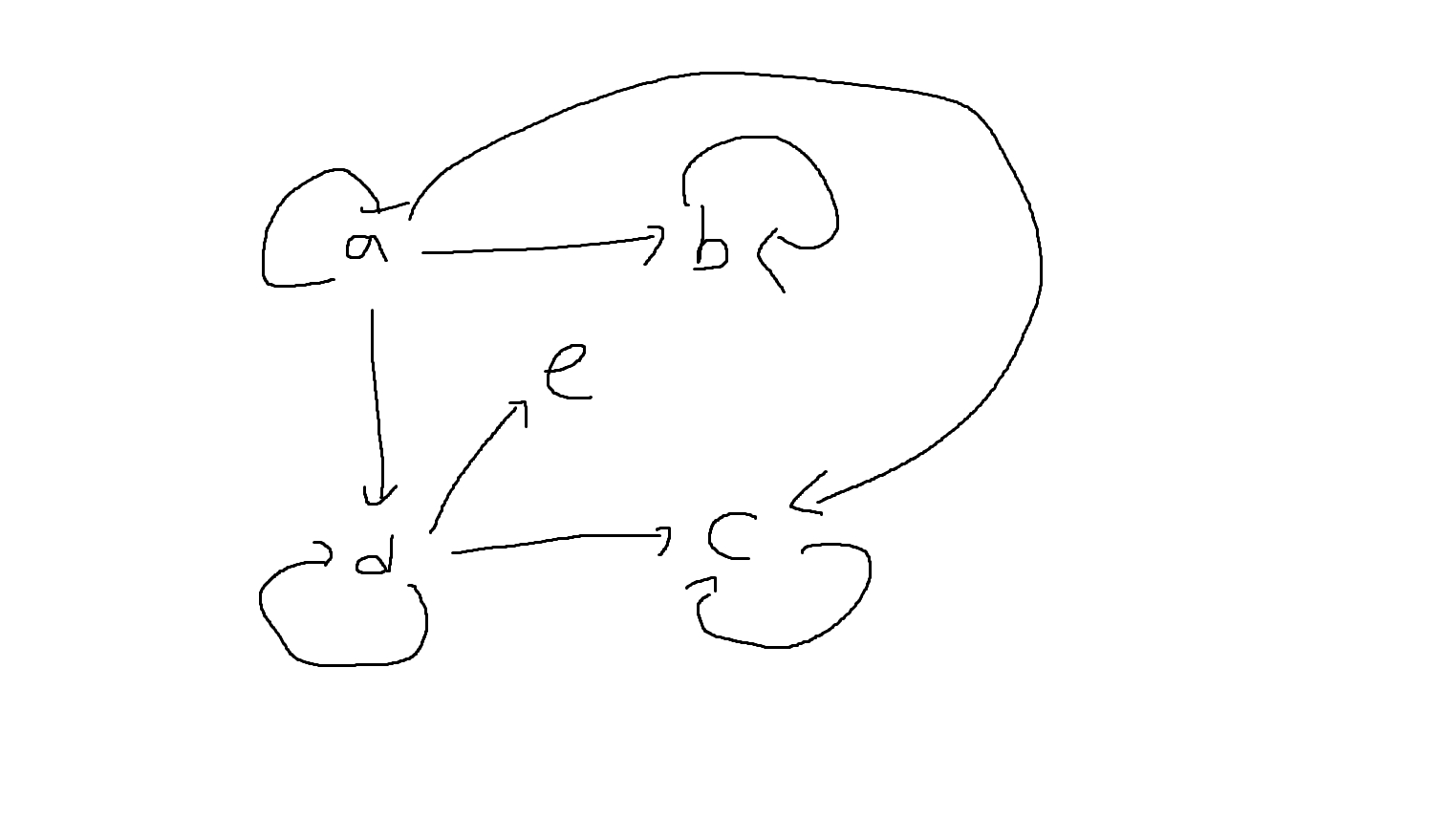
다음 방향성그래프에서 정점 a부터 시작하는 길이우선탐색(DFS)을 오름차순으로 수행할 경우 방문순서는?
(DFS는 반복해서 방문가능. 모든 곳 방문해야 됨)
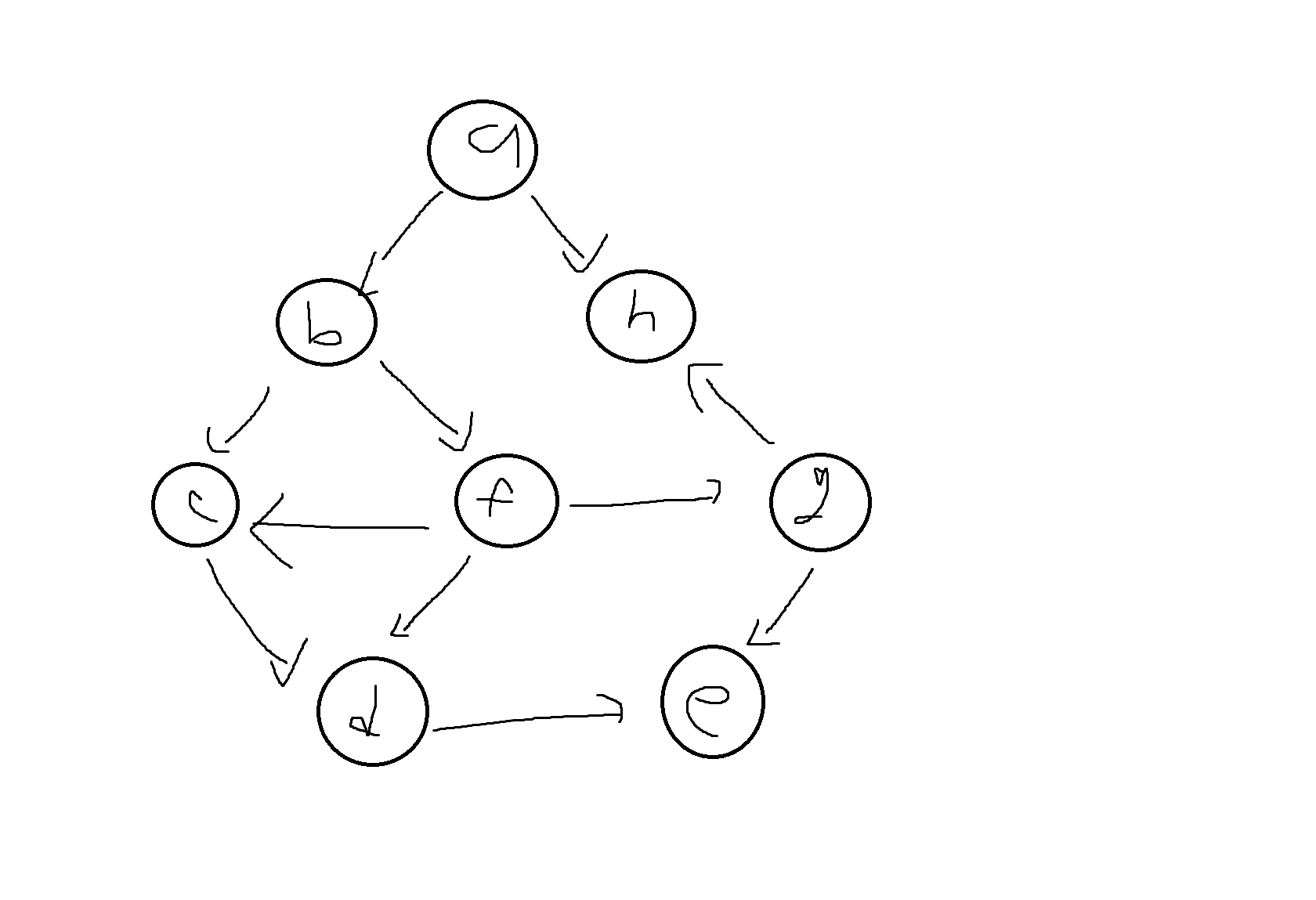
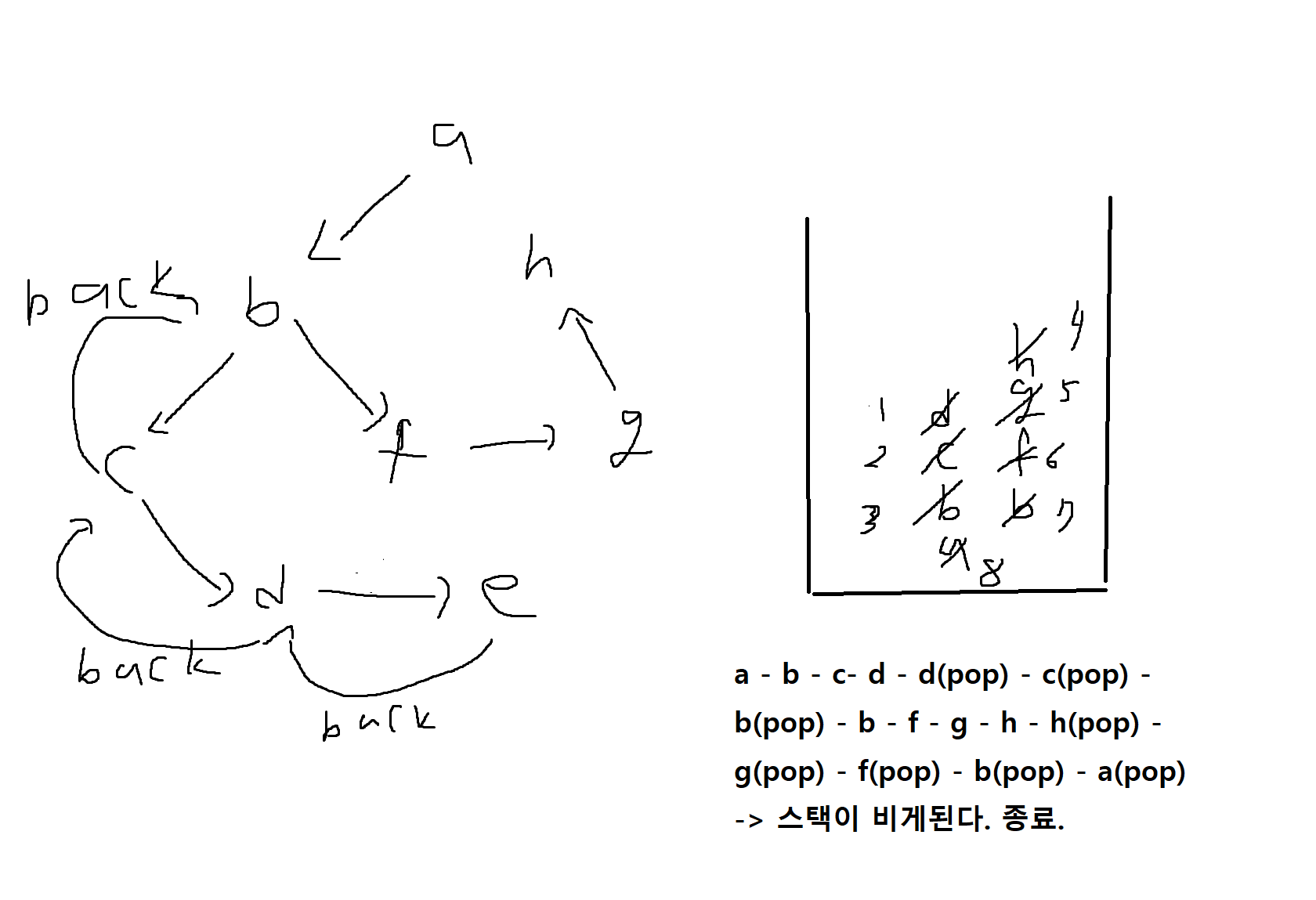
다음 방향성 그래프에서 정점 a부터 시작하는 너비우선탐색(BFS)을 오름차순으로 수행할 경우 방문순서는?
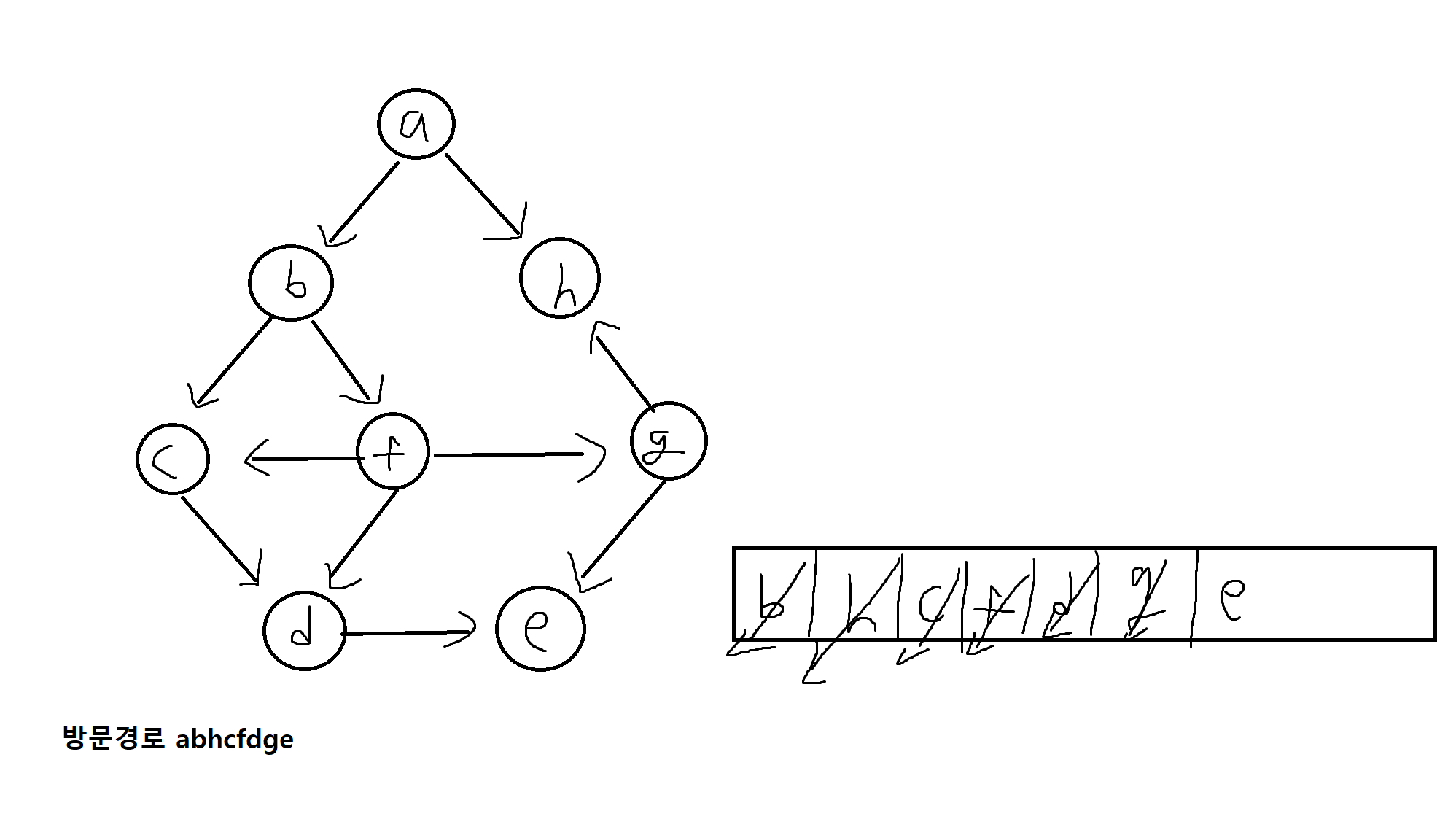
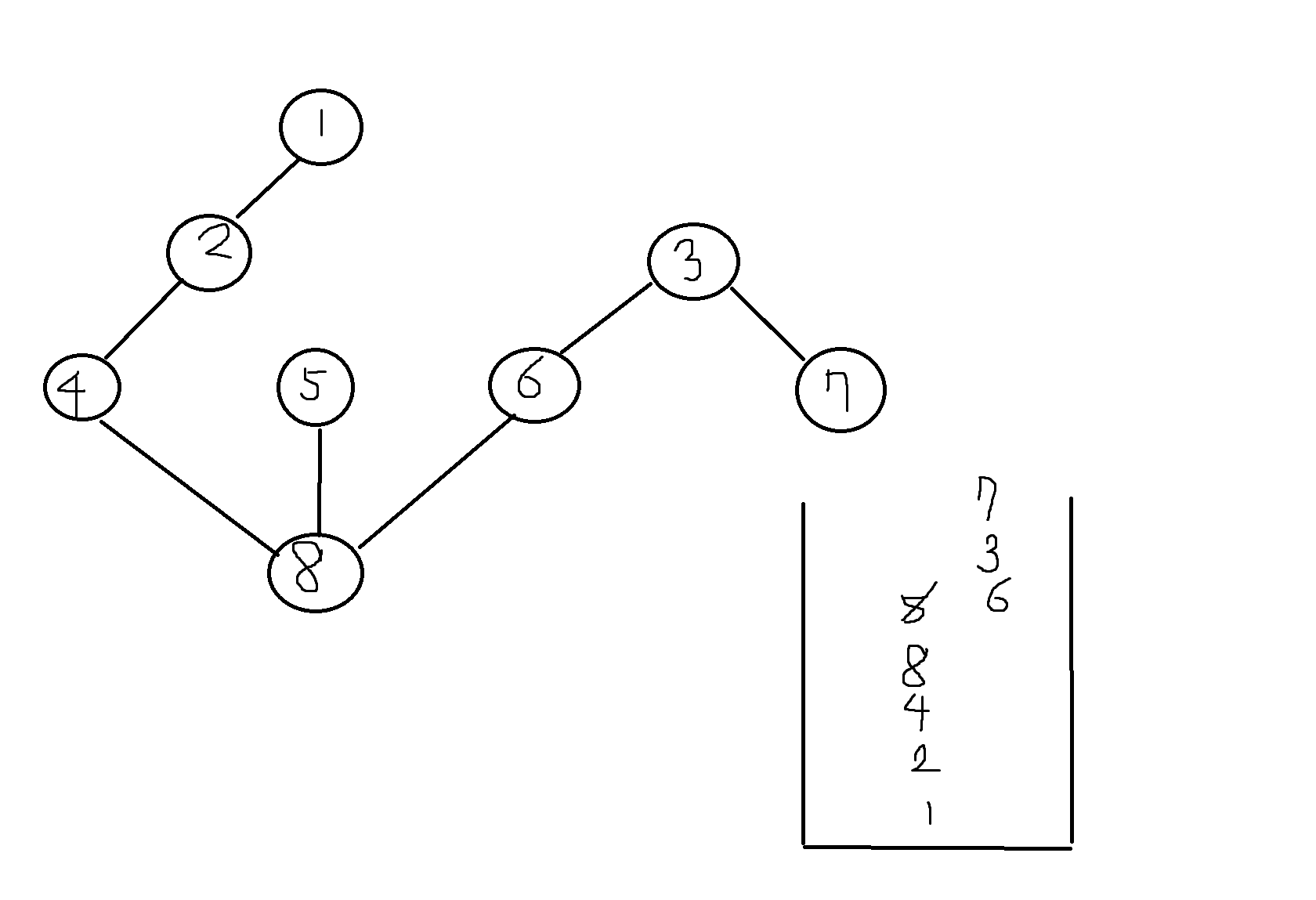
1부터 시작하고 작은 번호부터 탐색한다고 가정할때, BFS의 탐색결과는?
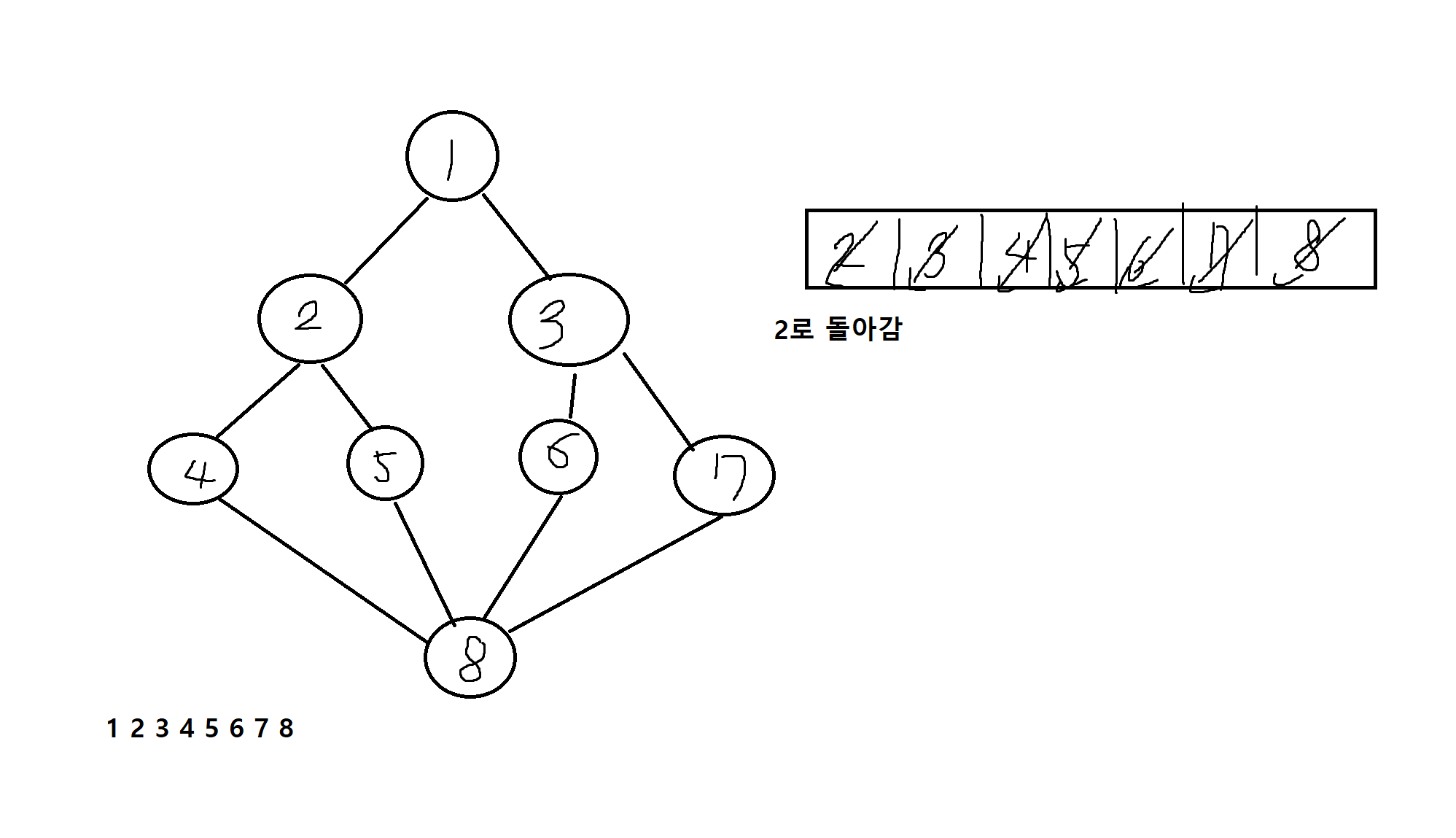
1) 다음 가중 그래프에서 최근접 이웃방법을 적용한 해밀턴 순회(정점 한번씩만 방문, 최소)를 만드시오. (A에서 시작함)
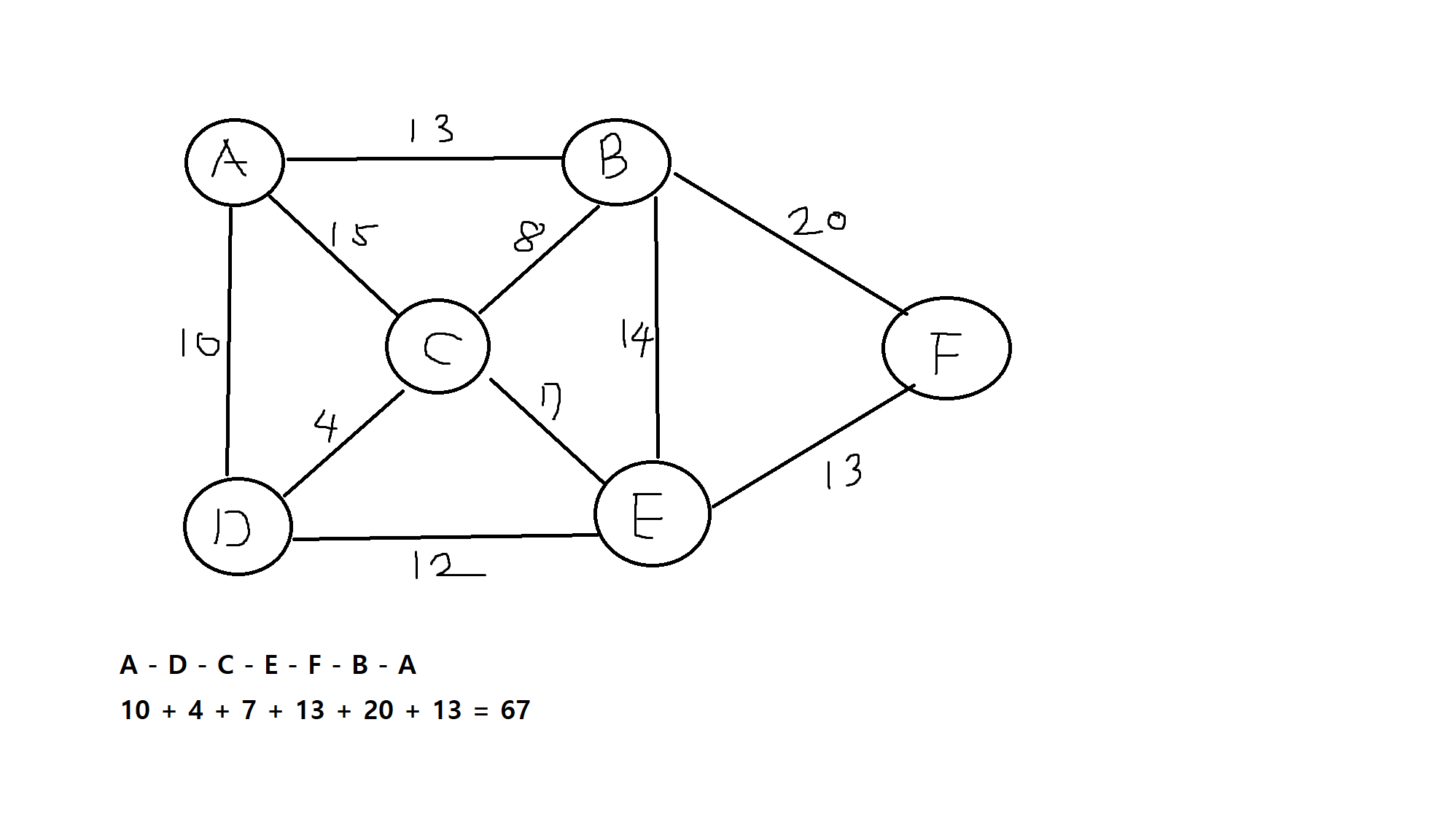
2) a에서 시작하고 알파벳 순서대로 탐색한다고 가정할 때, 깊이우선탐색(DFS)와 너비우선탐색(BFS)의 탐색결과는?
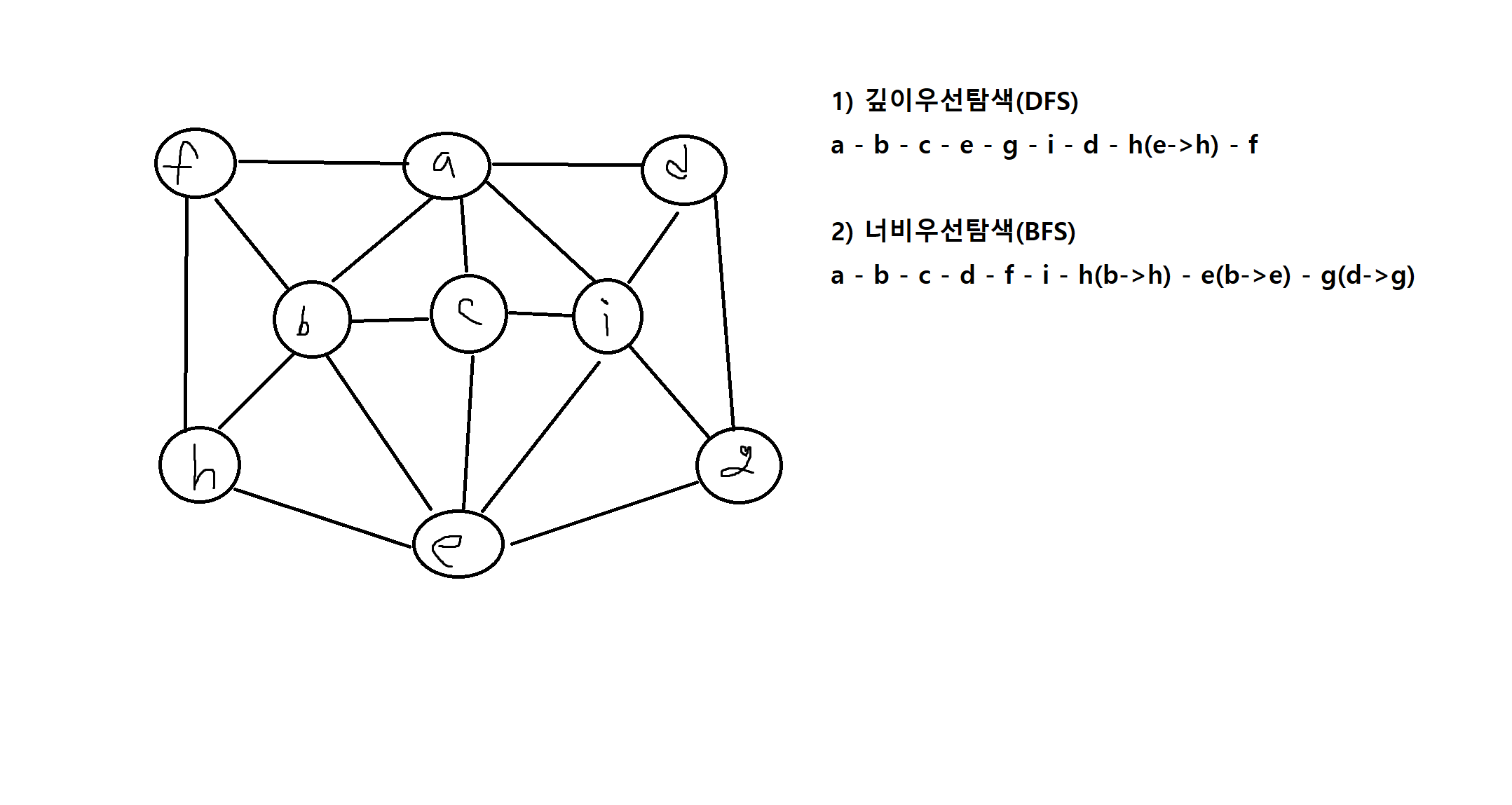
정의 7-20. 어떤 주어진 그래프 G에 대해 인접한 어느 두 영역도 같은 색이 안되도록 각 정점에 색을 칠하는 문제를 그래프 G의 색칠문제라고 한다. 그래프 G를 색칠하는데 필요한 최소한의 색의 수를 X(G)로 표현하고 G의 색칠수(Chromatic number)라고 한다.
- 단순그래프의 색칠은 각각의 정점을 서로 다른 색깔로 색칠함으로써 알 수 있음
- 대부분의 그래프에서는 정점의 수보다 적은 색깔을 사용해도 색칠이 가능함
예제 7-16. 다음 그림과 같이 경계가 주어진 지도를 색칠해보자. (서로 다른색)
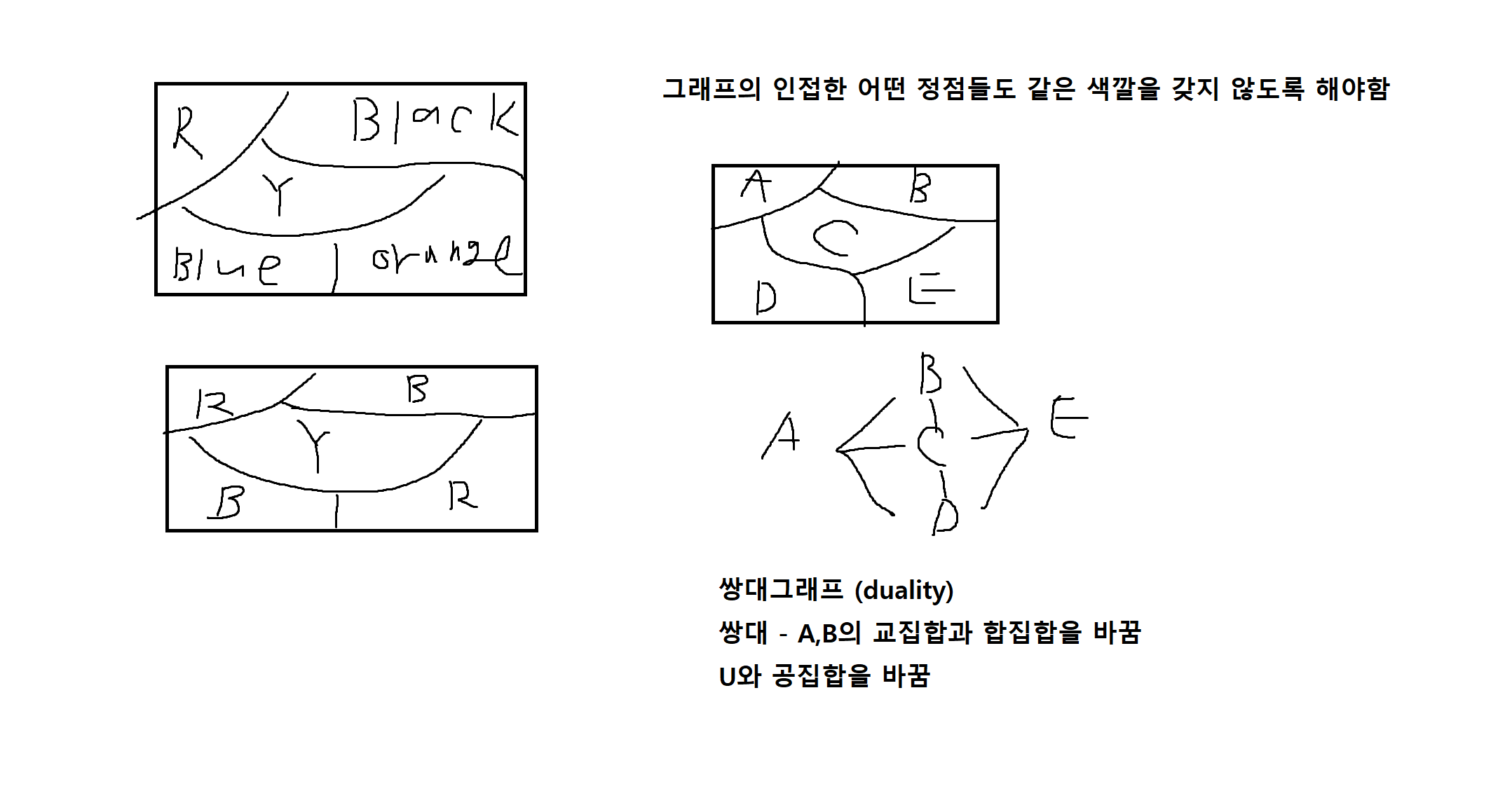
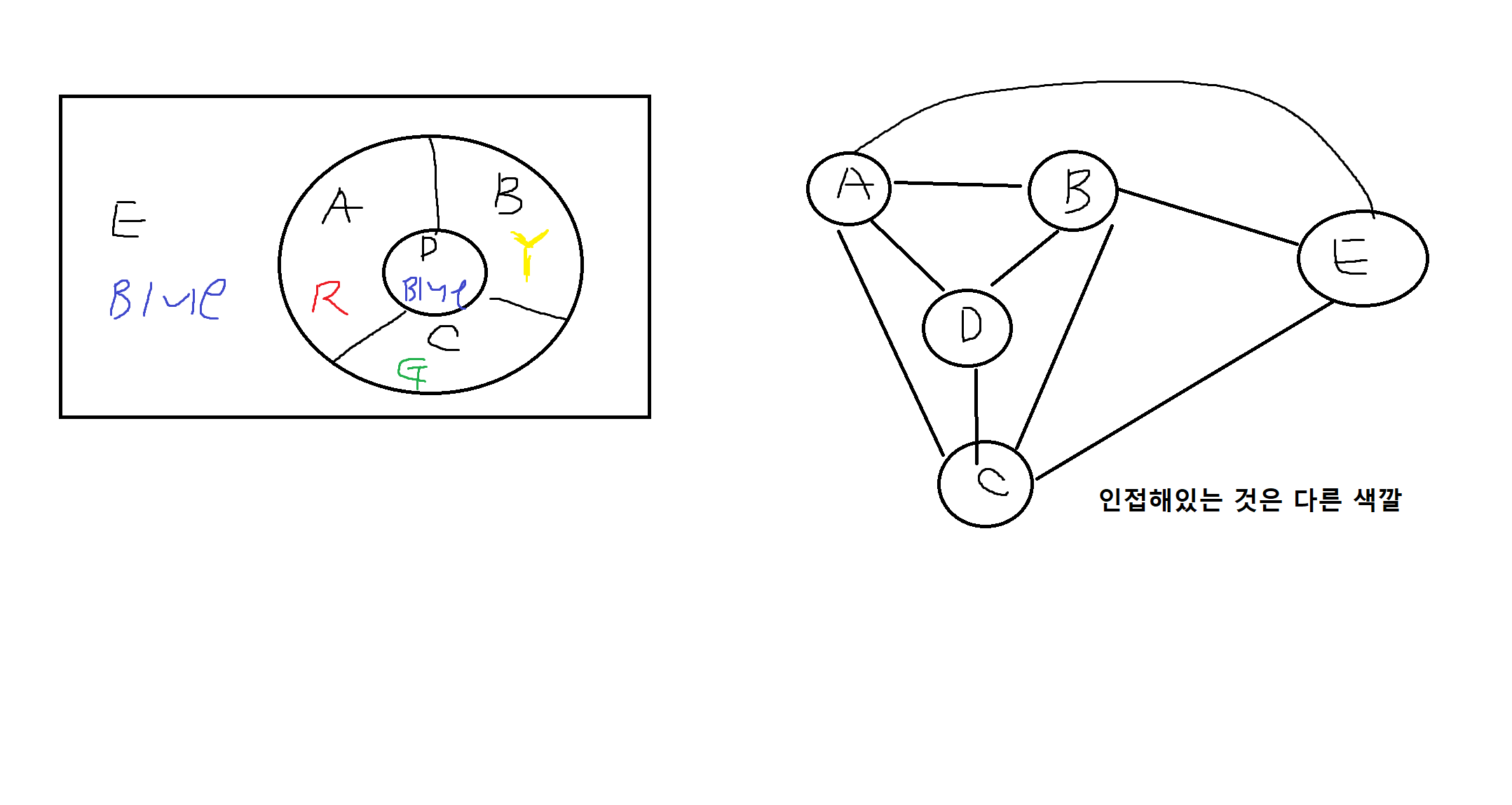
welch와 powell의 알고리즘
1) 주어진 그래프의 각 정점에서의 차수를 계산한다.
2) 구한 차수에 따라 내림차순에 따라 정점을 정렬한 수열을 만든다.
3) 정렬된 첫째 정점에 한색을 선택하여 칠하고 이 정점에 이웃하지 않는 정점을 수열에서 찾아 차례로 동일색을 칠한다. 단, 이웃하지 않는 정점끼리 서로 이웃하면 한 정점만 동일색을 칠한다.
4) 나머지 부분수열에 대해 같은 방법을 되풀이하며 모든 정점에 칠한 색이 정해질 때까지 시행한다.
(1. 차수 가장 큰 정점 색칠 - 2. 1과 인접하지 않는 점 같은색으로 3. 반복)
4색 문제
-
평면을 유한개의 부분으로 나누어 각 부분에 색을 칠할 때, 서로 맞닿은 부분을 다른 색으로 칠한다면 4가지 색으로 충분함
-
지도를 몇가지 색으로 칠할 수 있을까?
-> 둘러싼 나라가 짝수개라면 3가지 색, 홀수개라면 4개의 색이 필요함
정의 7-5. 그래프 G에 대해 다음은 서로 동치이다.
(1) G는 두가지 색으로 칠할 수 있다.
(2) G는 이분그래프이다.
(3) G의 모든 순환은 짝수의 길이를 가진다.
그래프의 컴퓨터 과학분야에서의 응용
-> 컴파일러, 논리회로, 플로우차트, 네트워크, 탐색/정렬...
연습문제
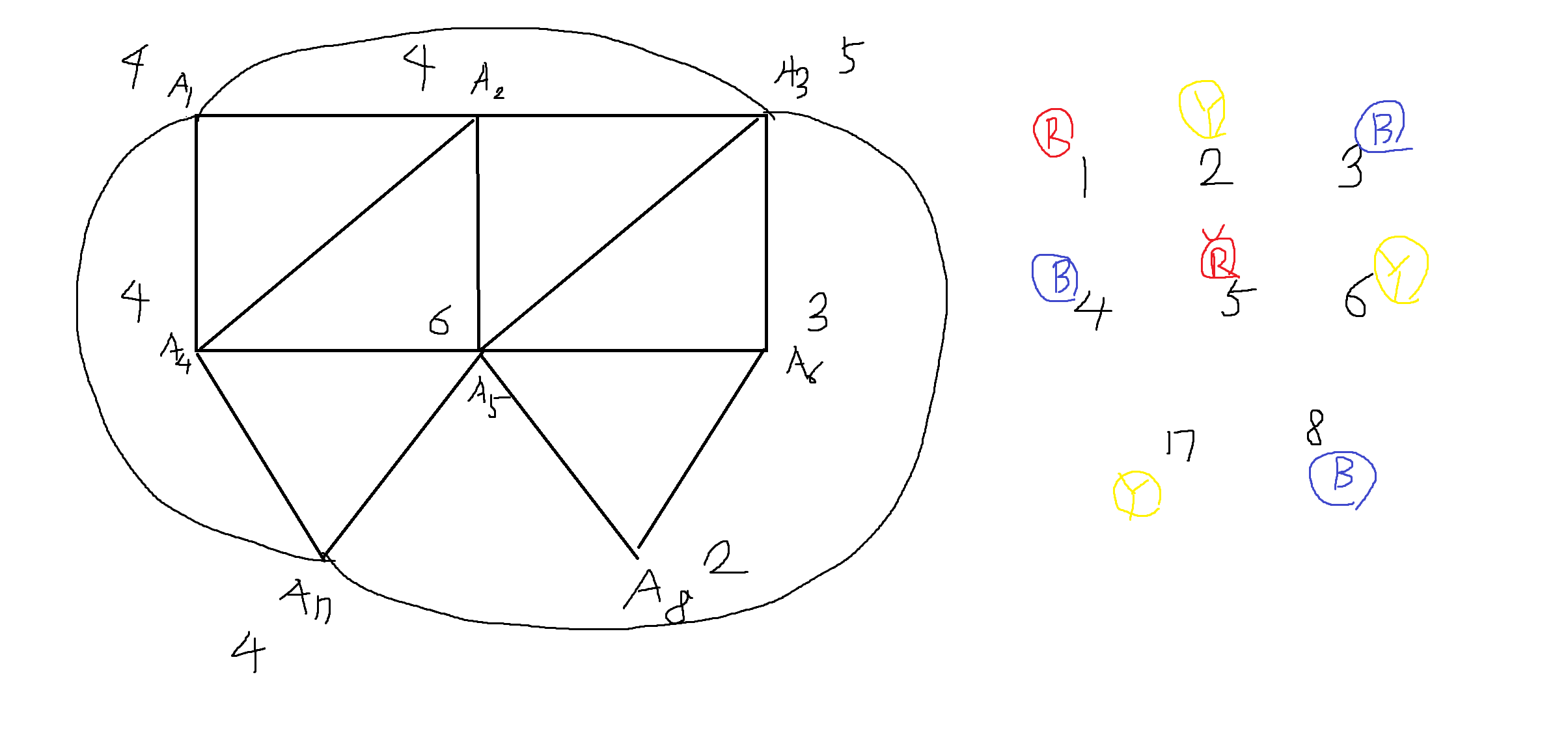
1) 각 정점은 한 국가이고 연결선은 국가간 인접함을 의미한다. 인접국가는 welch와 powell의 알고리즘을 이용하여 다른 색으로 칠할 때 최소로 필요한 색의 수는?
순서
1. 차수 제일 높은 정점 색칠
2. 1의 정점과 인접하지 않는거 같은색 칠함
2) R = {(a,b), (a,c), (a,d), (d,c), (d,e)}일 때 R+를 구하시오. 또한 R+를 나타내는 방향그래프를 구하시오
R+ = 임의의 정점에서 적어도 길이가 하나 이상인 경로로 도달할 수 있는 정점들의 쌍의 집합
R+ == R == {(a,b), (a,c), (a,d), (d,c), (d,e)}
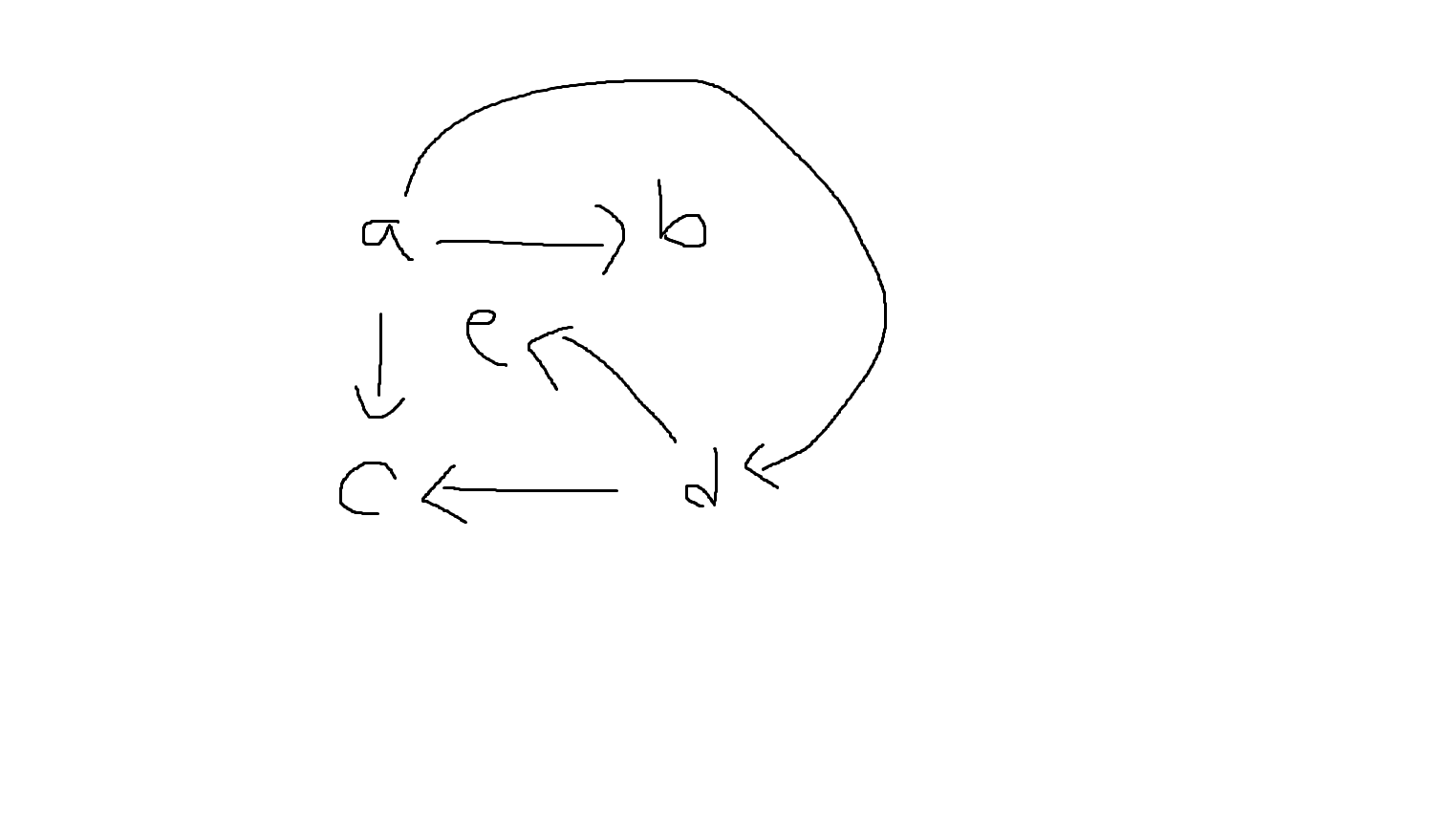
(3) R = {(a,b), (a,c), (a,d), (d,c), (d,e)}일때, R^ 를 구하시오. 또한 R^ 를 나타내는 방향그래프를 구하시오.
R^* (반사 및 transition) 자기자신으로 가는 것(반사) 추가
R^* = {(a,b), (a,c), (a,d), (d,c), (d,e), (a,a), (b,b), (c,c), (d,d)}