그래프 이론
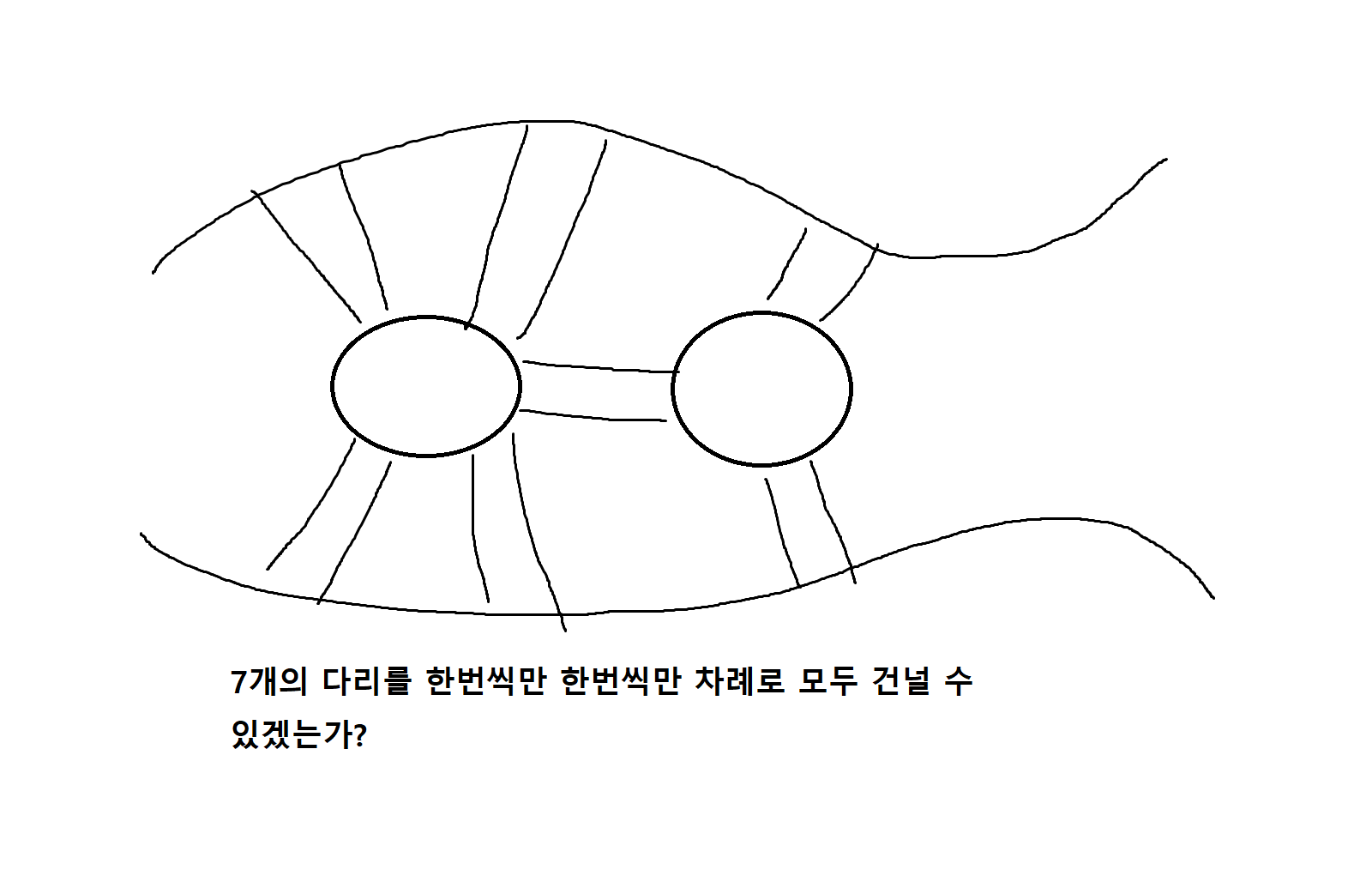
-> 쾨니히스베르크 다리문제
정의 7-1. 그래프 G=(V,E)는 유한한 개수의 정점(Vertex) 또는 노드(Node)들의 집합인 V와 연결선(edge) 또는 에지라고 불리는 정점들의 쌍의 집합인 E로 이루어진다.
G = (vetex, edge)
그래프의 2가지 종류
- 방향그래프 - 방향이 있는 그래프
- 방향이 없는 그래프
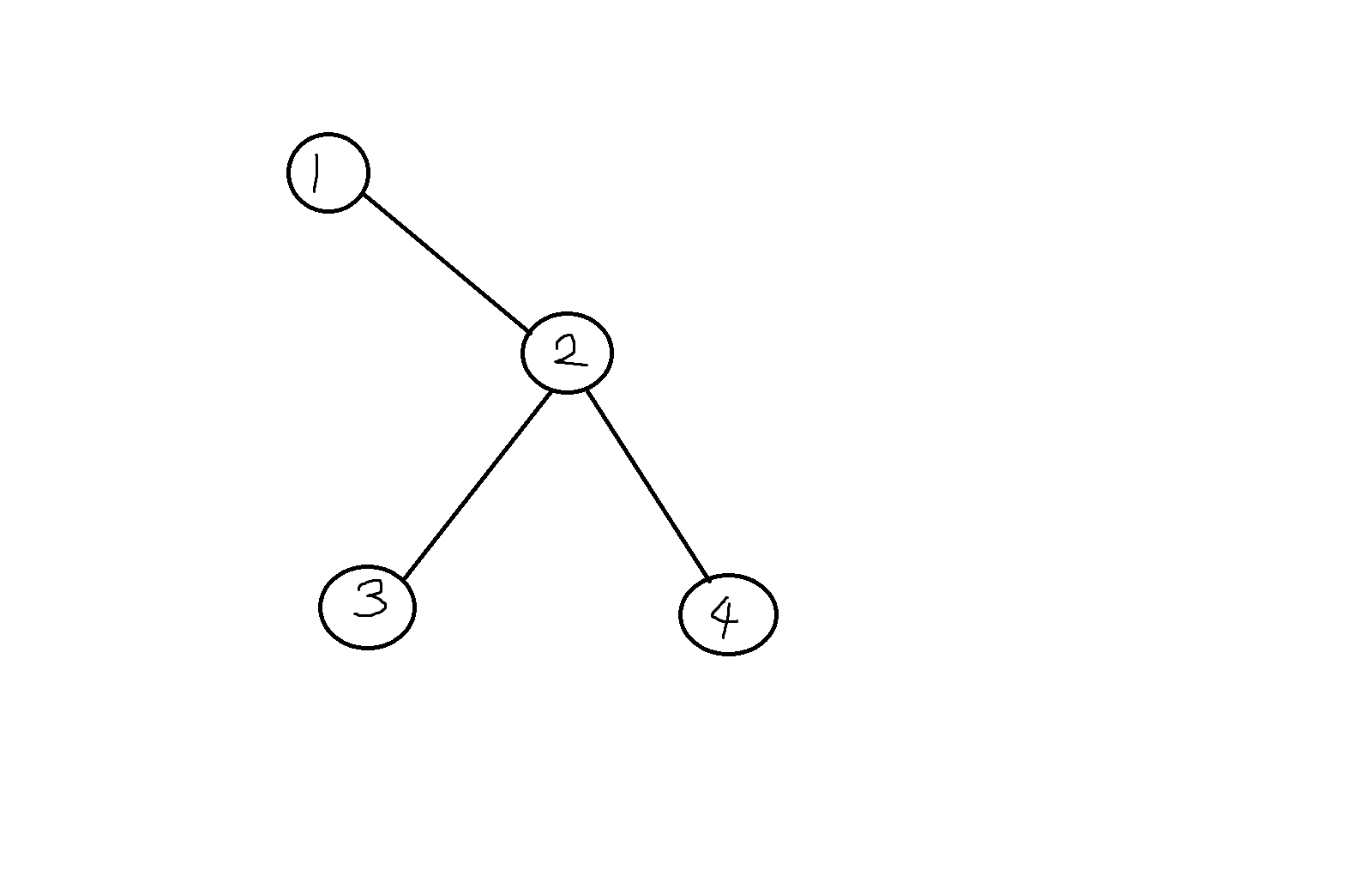
간단한 예
V = {1,2,3,4}
E = {(1,2), (2,3), (2,4)}
사이클(cycle)
v₁ = vk (k!=1)이면 이러한 경로를 사이클이라 함 (시작점과 끝점이 같음)
경로(path)
- 모든 1<=i<k에 대해 연결선(Vi, Vi+1)이 존재할 때, 정점들의 열 V₁,V₂,V₃,... Vk라고 한다.
- k>=1이며 이 경로의 길이는 k-1 임
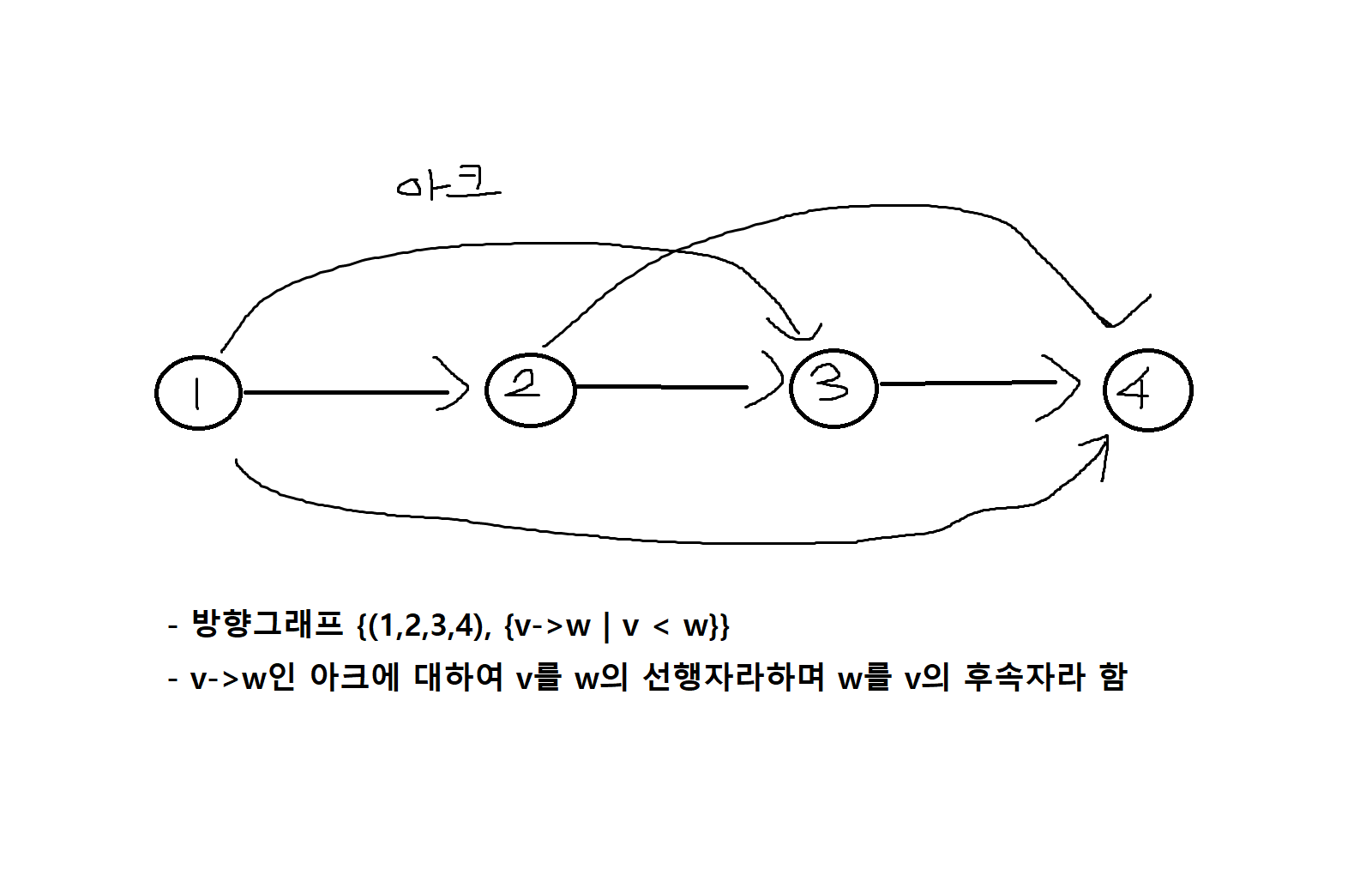
정의 7-2. 방향그래프 또는 다이그래프는 G = (V, E)로 표시한다. 여기서 V는 정점들의 집합이며, E는 정점들의 순서화 된 쌍인 아크(arch) 또는 연결선들의 집합이다. 정점 v에서 정점 w로 가는 아크는 v->w로 표시한다.
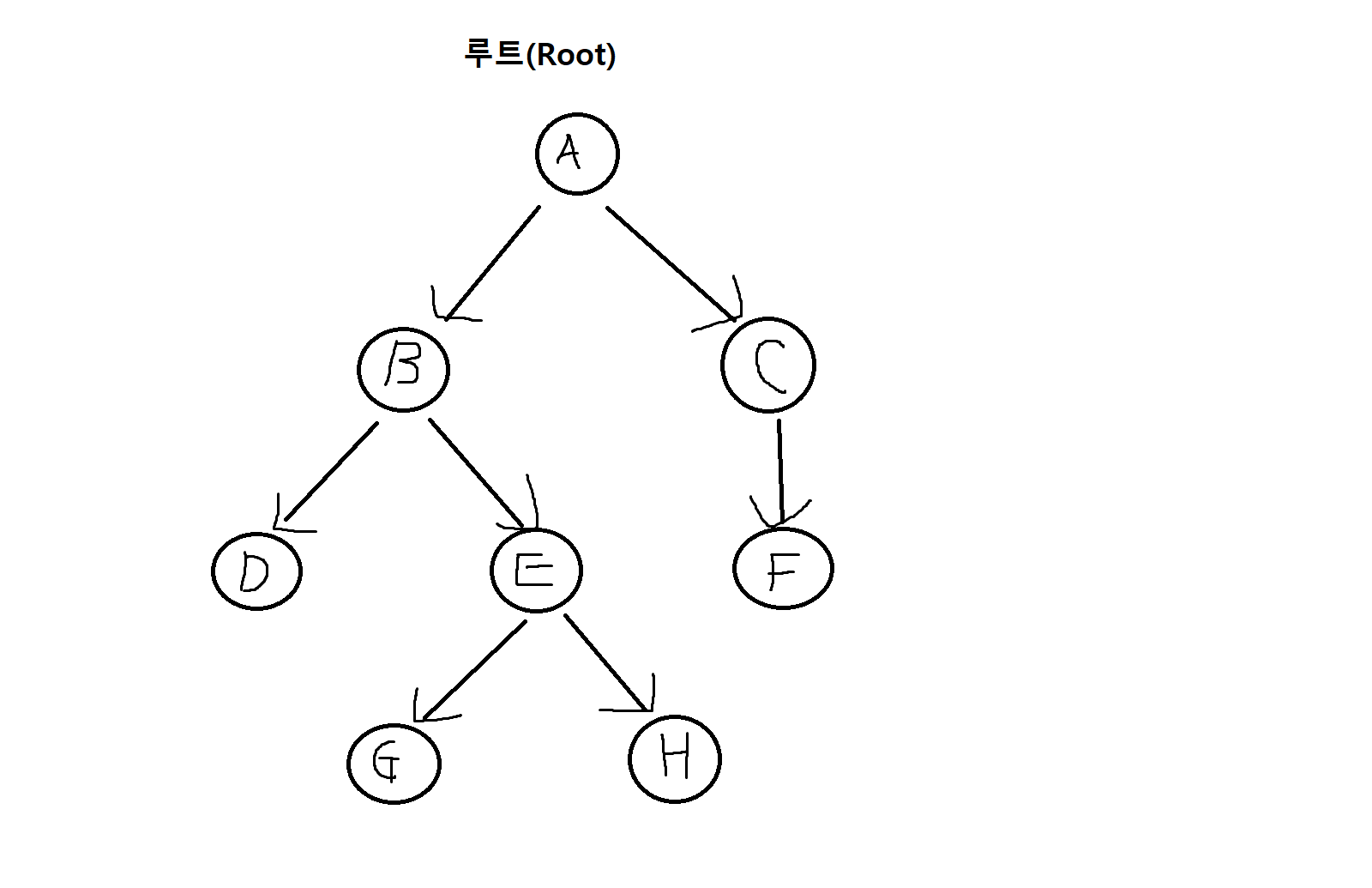
트리(Tree)
- 사이클이 존재하지 않는 그래프임
- 루트(Root)라 불리는 특별한 노드가 한개 존재하고, 루트로부터 다른 모든 노드로 가는 경로가 항상 유일하게 존재함.
- 루트로 들어오는 연결선이 없으므로 루트는 모든 트리의 출발점이 됨
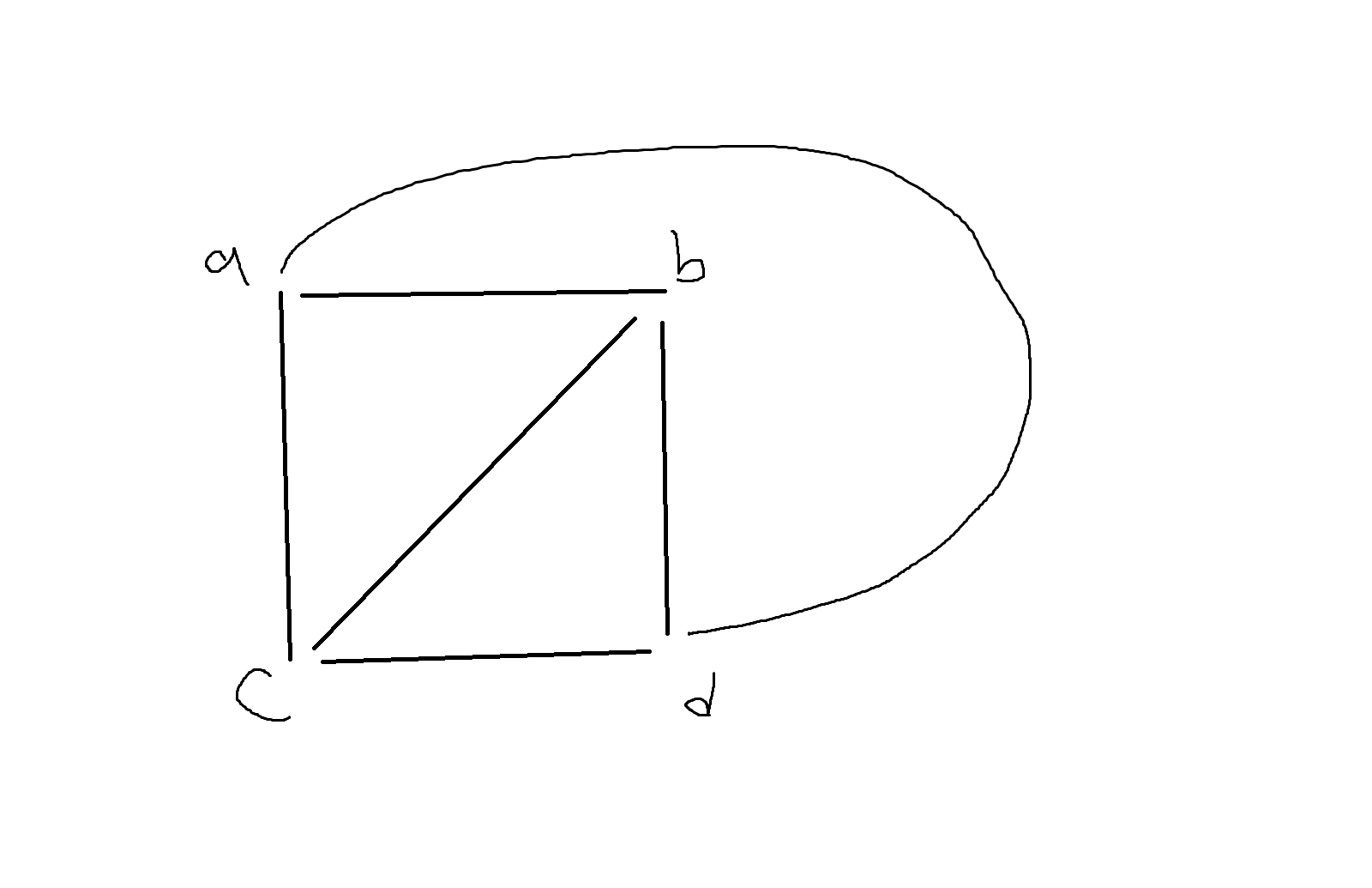
정의 7-3. 단순그래프
- 한쌍의 정점 사이에 많아도 하나의 연결선으로 이루어진, 우리가 통상 다루는 그래프로서 자기 자신으로의 연결선이 없는 그래프이다.
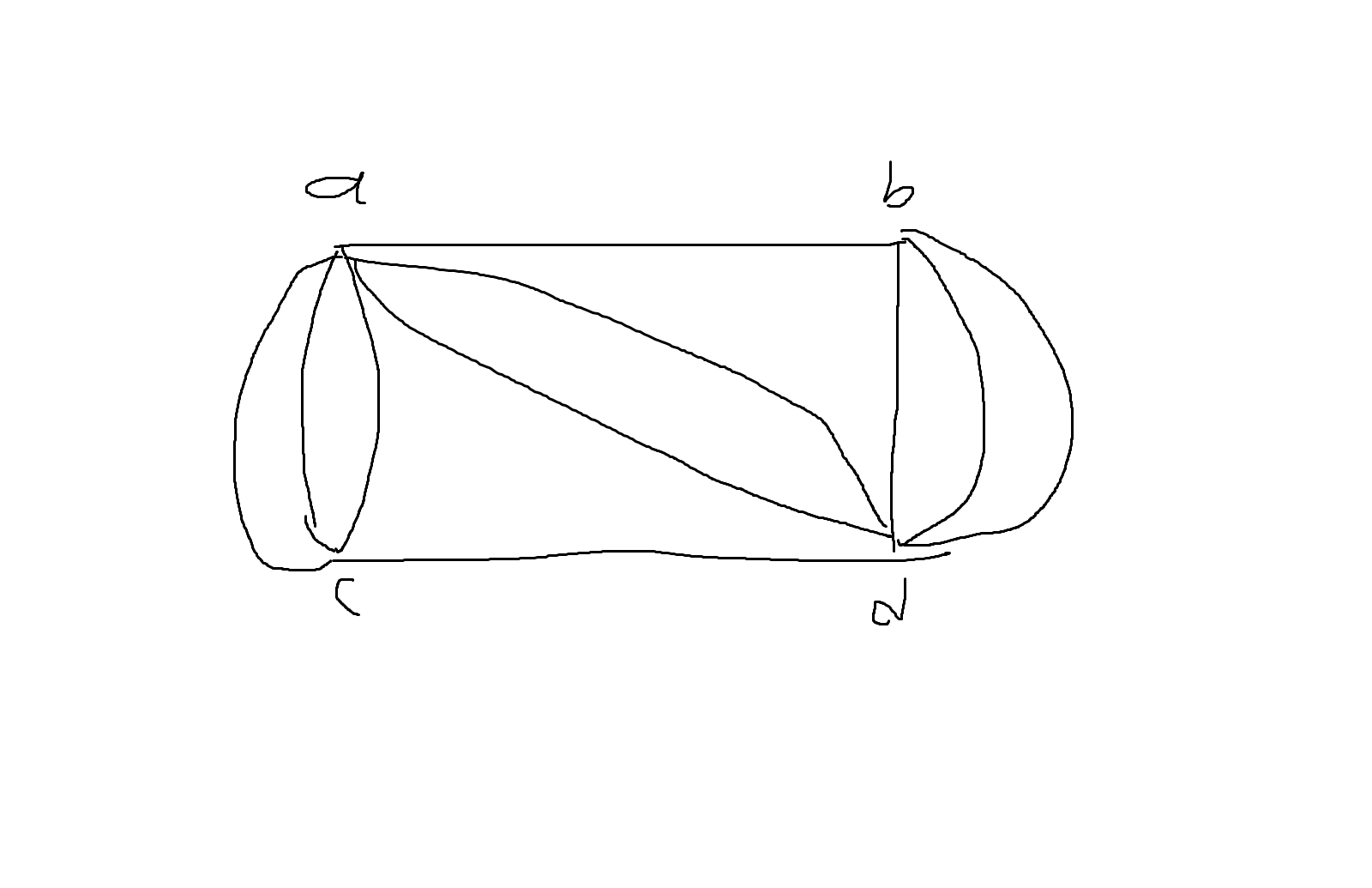
멀티그래프
단순그래프의 확장. 한쌍의 꼭지점 사이에 연결선의 개수의 제한이 없는 일반적인 그래프
정의 7-5. 그래프 G = (V, E)에서 순서화된 쌍 E를 그래프의 연결선(Edge)라고 한다. (u,v) ∈ E 일때 u와 v를 연결하는 연결선 e는 u와 v에 "접했다"(incident)라고 하고 u와 v로 서로 "인접했다"(adjacent)라고 한다.
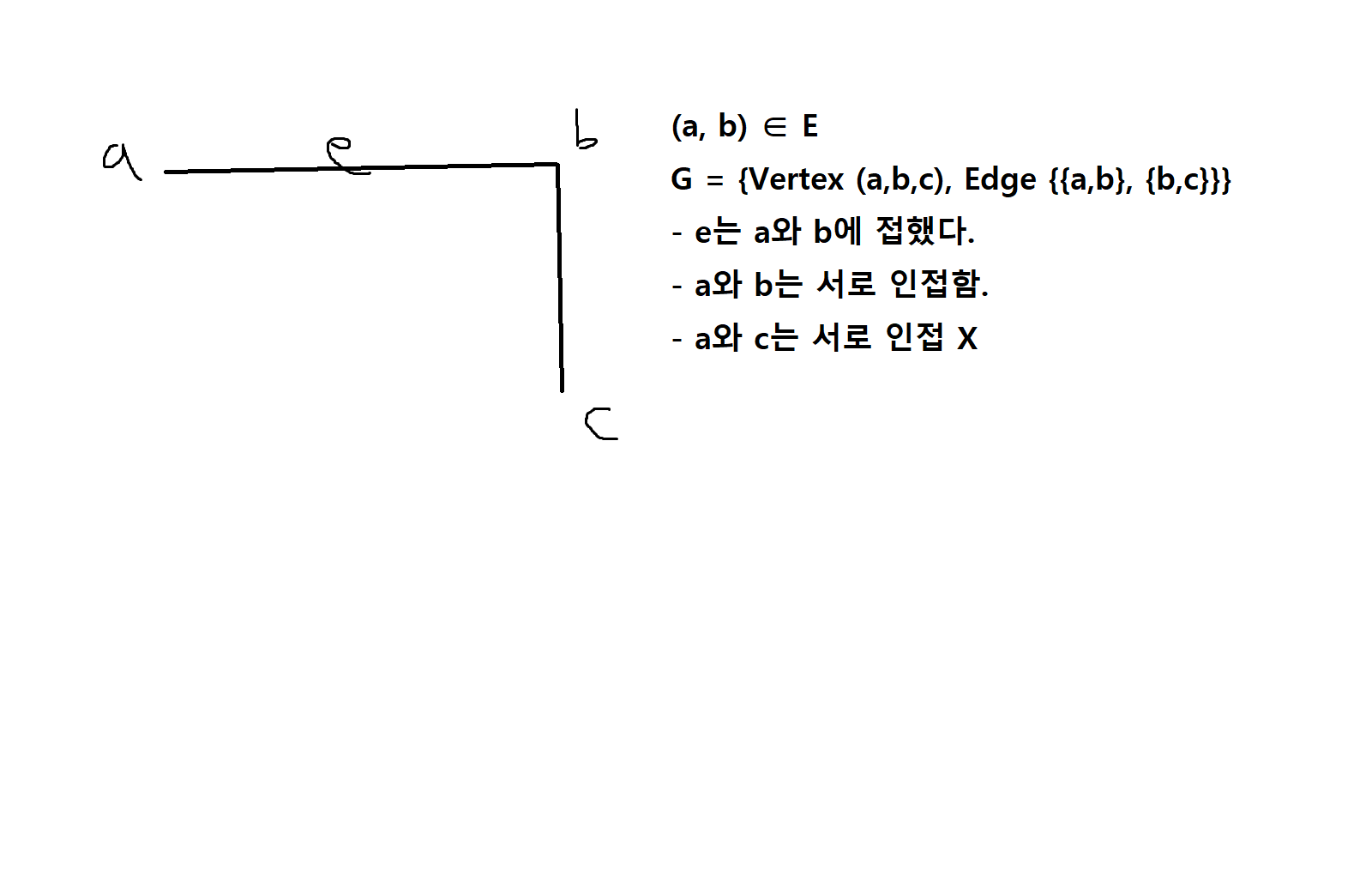
정의 7-6. G = (V, E)가 그래프이고 u,v가 꼭지점이라고 할때, V의 차수(degree)는 V에 인접하는 연결선의 개수
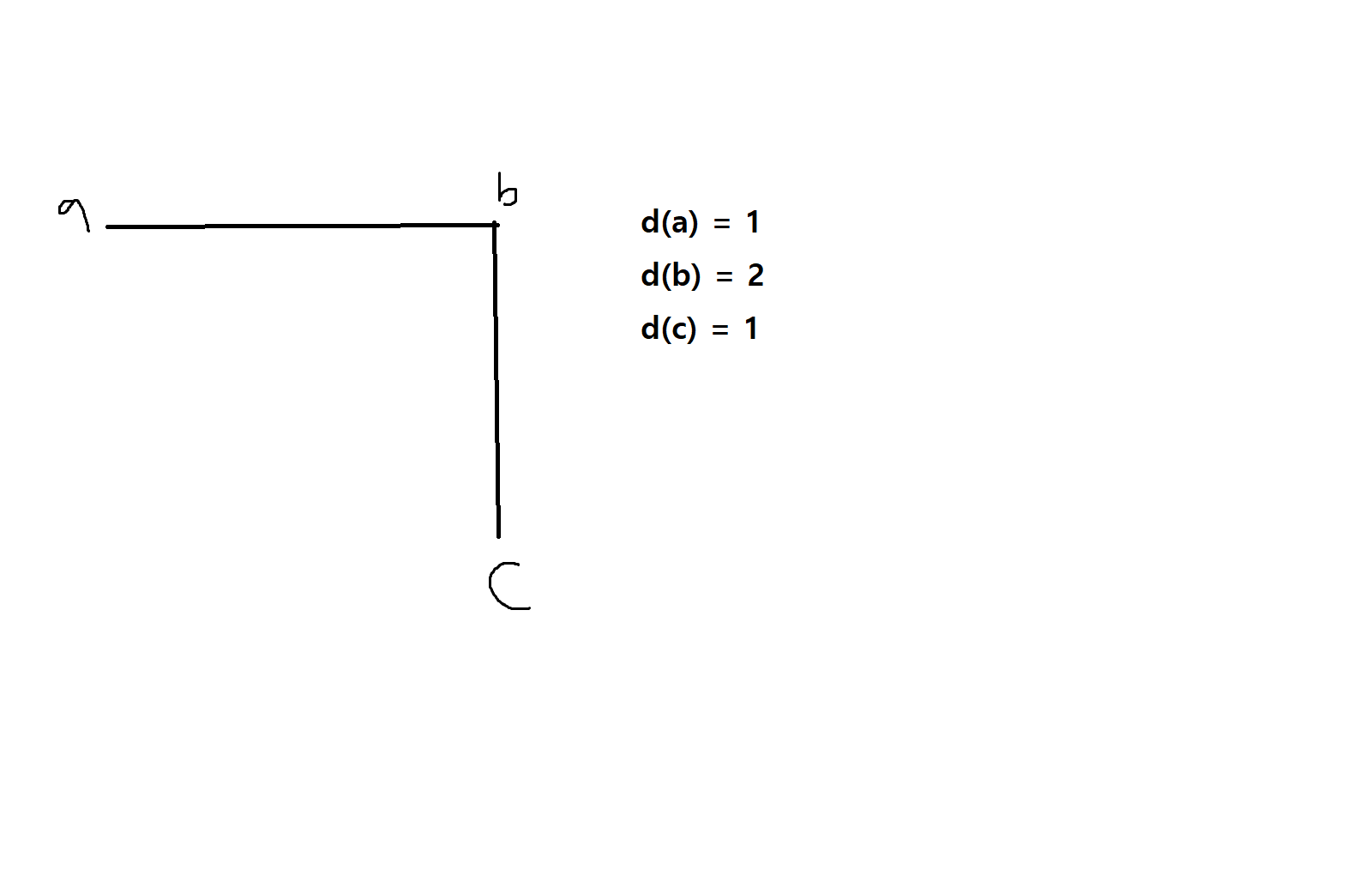
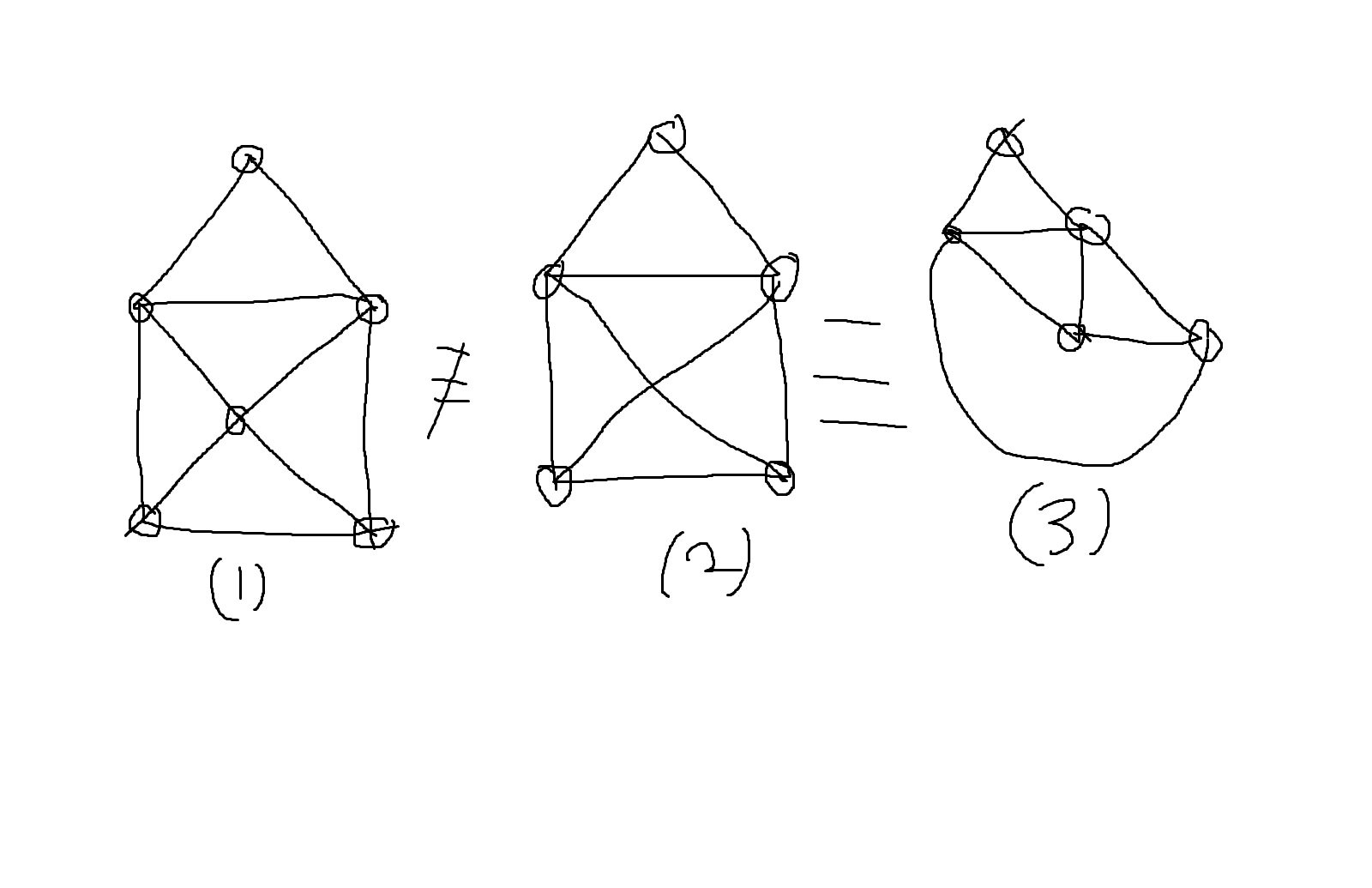
정의 7-7. 두개의 그래프 G = (V,E), G' = (V',E')에서 V'⊂=V, E'⊂=E 일 때 그래프 G' = (V',E')를 G의 부분 그래프라고 한다. 이때 V = V'이고 E'⊂E이면 G'는 G의 생성 부분그래프 라고한다.
예제 7-1. 다음 그림의 (2)는 V'⊂=V, E'⊂=E 이므로 (1)의 부분그래프이다. 또한 (2)는 V=V'이고 E'⊂E이므로 (1)의 생성부분그래프도 된다.
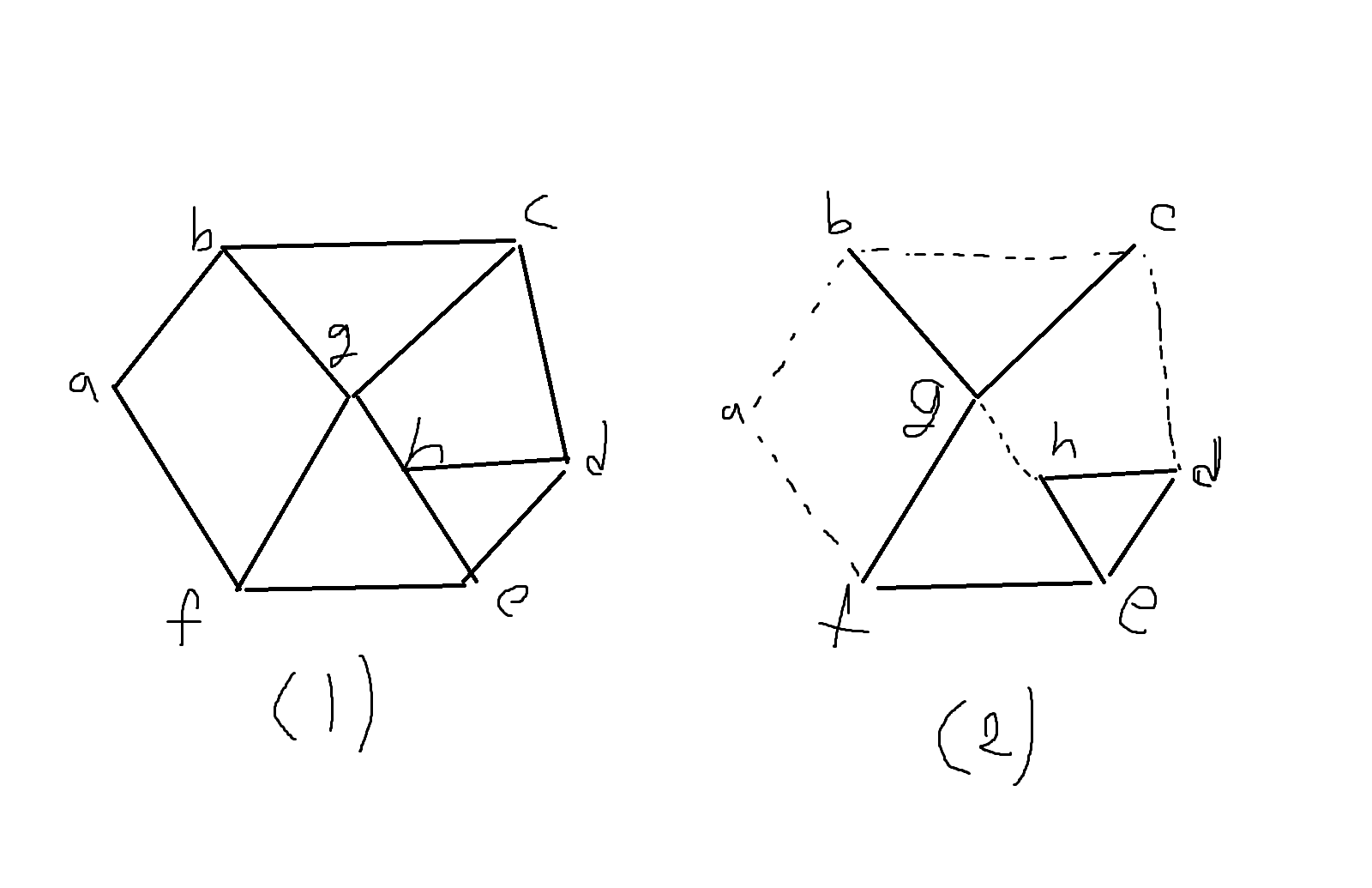
(1) 경로 (Path)
- 그래프에서의 경로란 꼭지점의 열 V₁,V₂...Vn에서 (Vk-1, Vk) ∈ E, 1<k<=n인 경우를 말함
- 경로의 길이는 n-1임
(2) 단순경로 (Simple path)
- 경로가 같은 연결선을 두번 포함하지 않는 경로를 말함
(3) 기본경로 (elementary path)
- 어떤 정점들도 두번 만나지 않는 경로를 말함
(4) 사이클(cycle) 또는 순회(circuit)
- 경로 (v₁,v₂,vn)에서 종점 vn과 시작점 v₁이 일치하는 경우를 말함
(5) 단순 사이클 (Simple cycle)
- 같은 연결선을 반복하여 방문하지 않는 사이클을 말함
(6) 기본사이클
- 시작점을 제외한 어떠한 정점도 반복하여 방문하지 않는 사이클을 말함
정의 7-9. 그래프에서 정점들간의 연결여부에 따라 연결그래프, 강한 연결그래프 등이 정의된다.
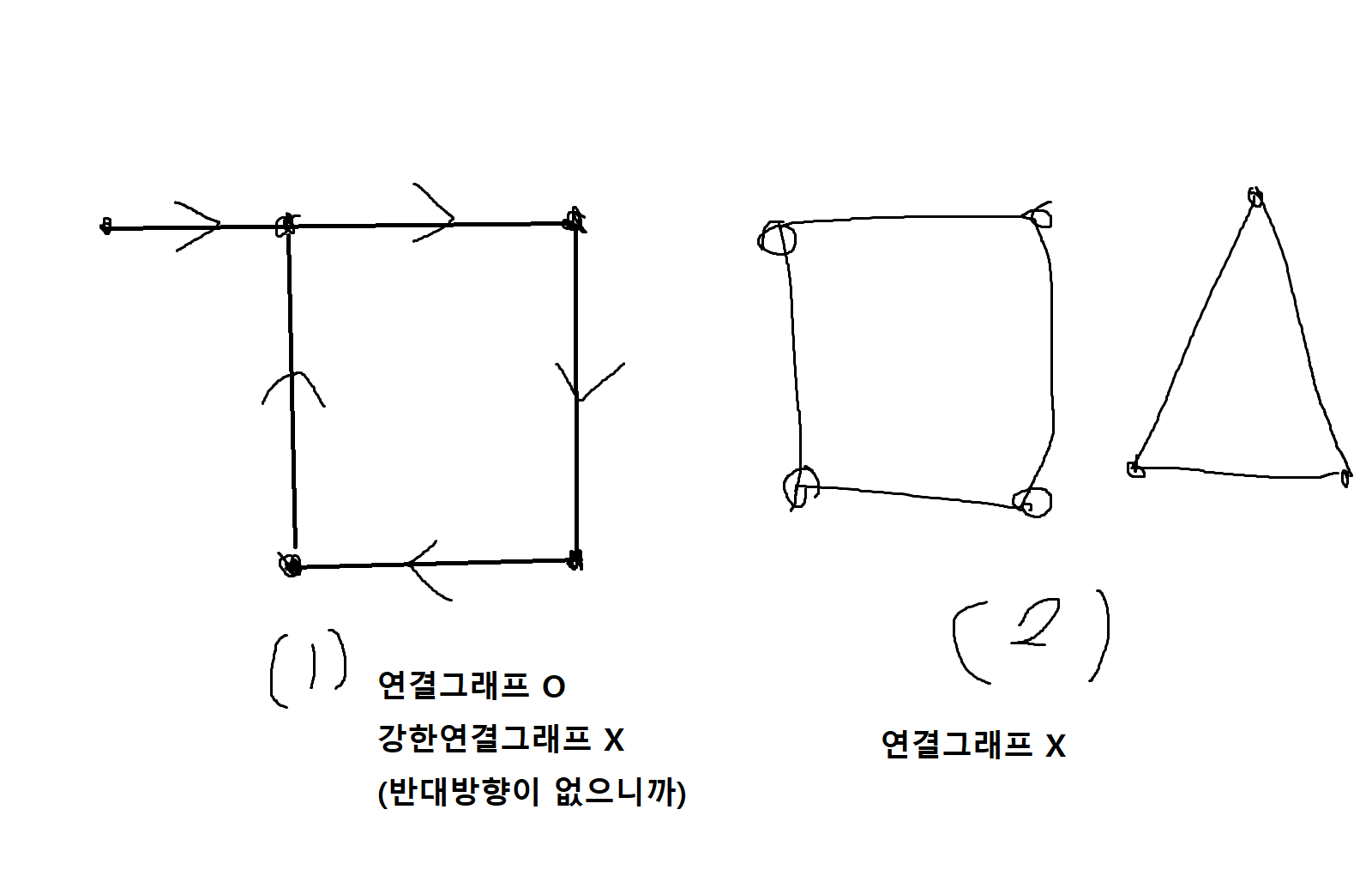
(1) 연결그래프 (connected graph)
그래프의 모든 정점들이 연결되어 있는 그래프
(2) 강한 연결그래프 (strongly connected graph)
그래프에서 모든 두 정점 a와 b에 대해서 a에서 b로의 경로와 b에서 a로의 경로들이 존재하는 그래프를 말하는데, 특히 방향 그래프에서 의미를 가짐
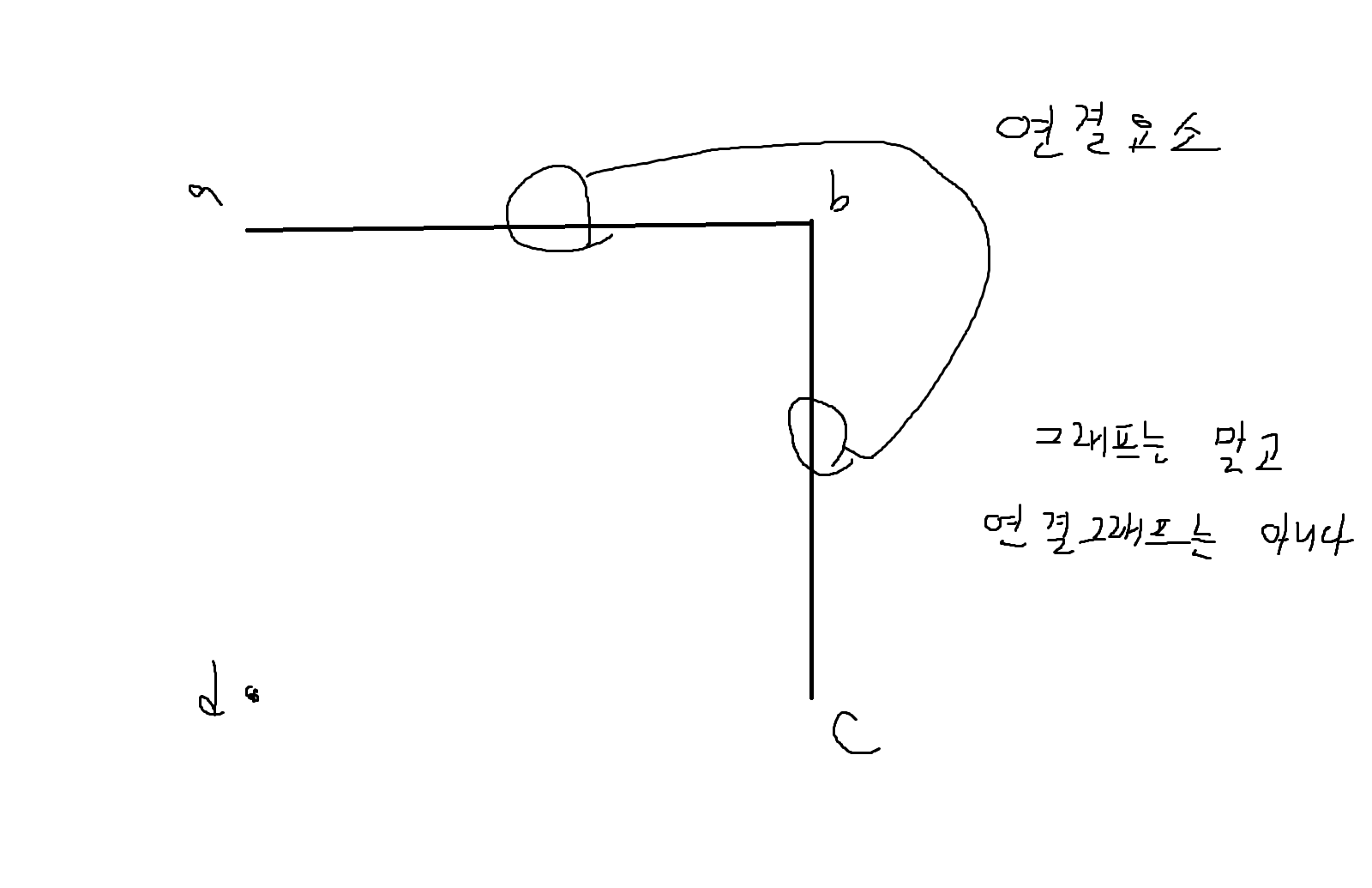
(3) 연결요소 (connectivity component)
그래프에서 모든 정점들이 연결되어 있는 부분을 말하며, 연결수 (connectivity number)란 그래프 G에서의 연결요소의 개수를 말함
예제 7-2. 다음 그림이 연결그래프인지 강한 연결그래프인지 판단해보라
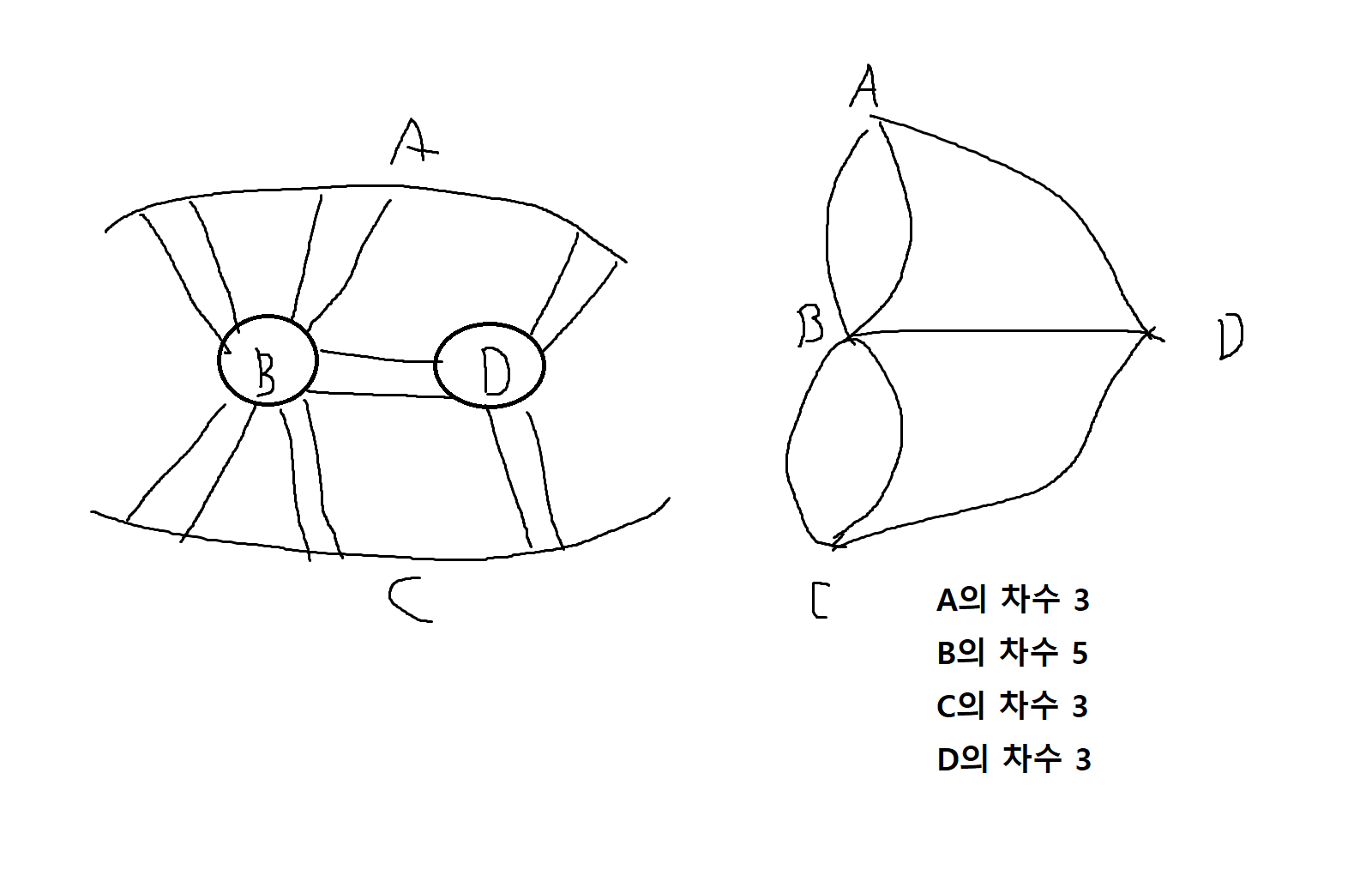
- 멀티그래프란 한쌍의 정렬 사이에 연결선의 개수의 제한이 없는 중복된 연결선을 허용하는 특별한 그래프임.
- 쾨니히스베르크 다리 문제를 해결하는 방법은 멀티그래프를 모델링 하는 것임
-
멀티그래프에서의 오일러의 경로를 판별하는 규칙은 모든 정점에서 그것에 연결된 연결선의 개수(차수)가 홀수인 정점(홀수점)의 개수가 0 또는 2인 경우임
-> 따라서 이 경우 각 다리를 꼭 한번씩만 건너는 경로가 존재하지 않음 -
아래 그림의 (1)과 (2)는 위상적으로 다르지만, (2)와 (3)은 위상적으로 같음
요약
- 그래프 G = (V, E)는 유일한 개수의 정점 또는 노드들의 집합인 V와 연결선 또는 에지라고 불리는 정점들의 쌍들의 집합인 E로 이루어진다.
- 그래프는 방향이 있는 그래프인 방향그래프와 방향이 없는 그래프의 2가지로 구분된다.
- 멀티그래프는 단순 그래프의 확장으로서 한쌍의 꼭지점 사이에 연결선의 개수가 제한이 없어진 일반적인 그래프이다.
- 멀티그래프에서 모든 연결선들은 꼭 한번만 통과할 수 있는 경로를 오일러 경로라고 하는데 쾨니히스베르크 다리 문제는 오일러 경로를 찾을 수 있는지 여부와 동치이다.
연습문제
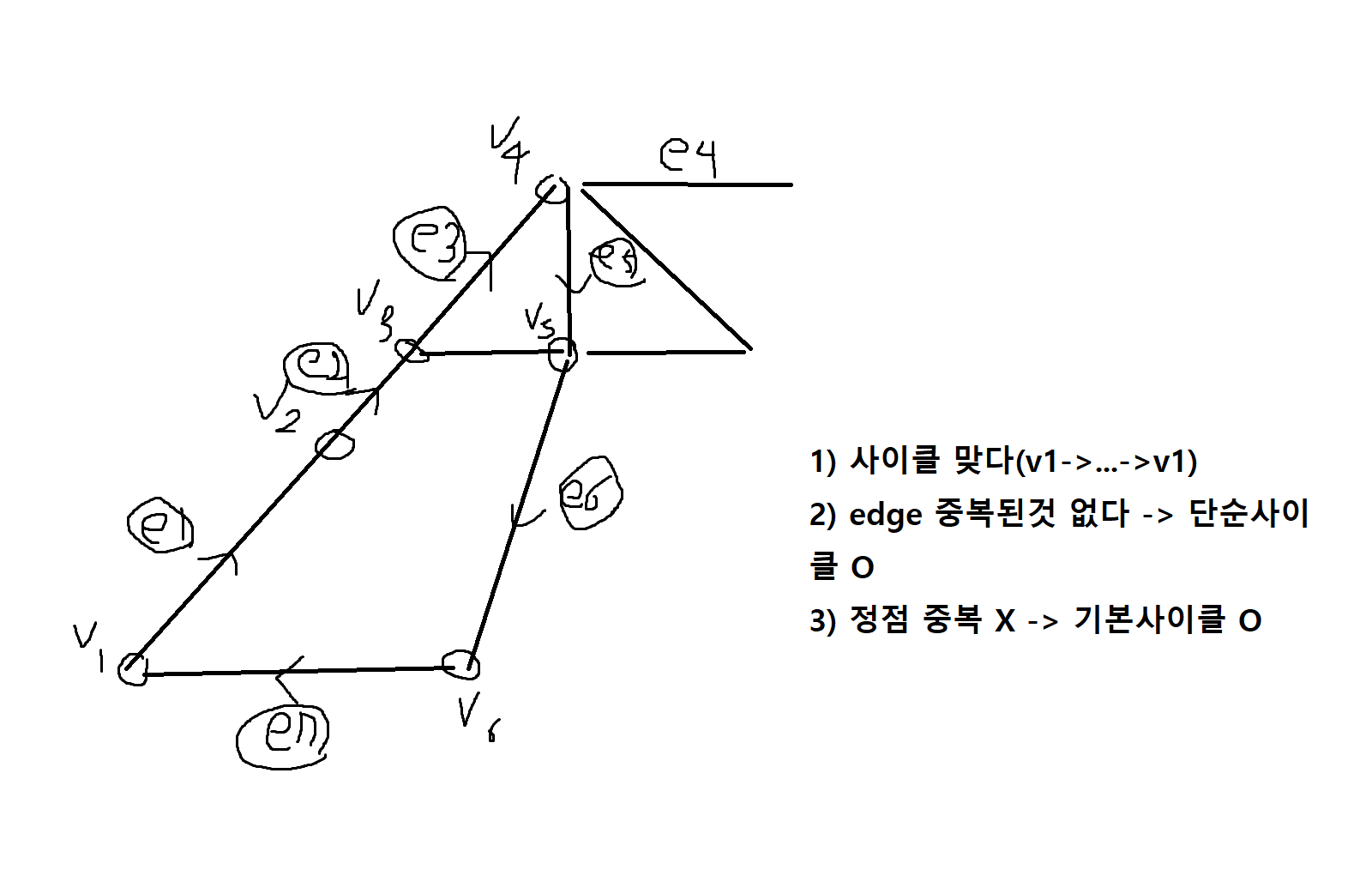
1) (e₁,e₂,e₃,e5,e6 e7)은 단순사이클(연결선)인가? 기본사이클(정점)인가?
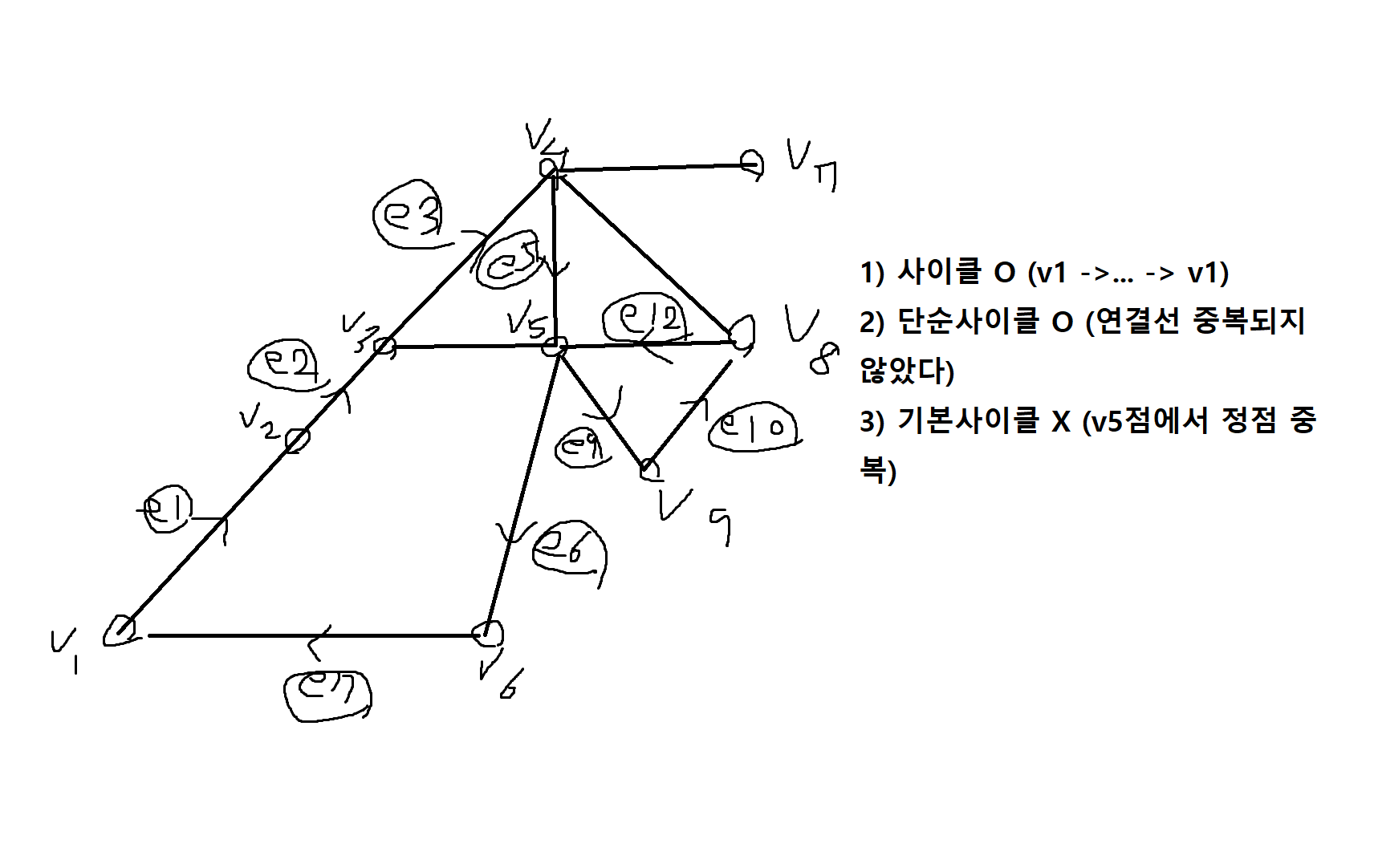
2) (e1, e2, e3, e5, e9, e10, e12, e6, e7)은 단순사이클(연결선)인가? 기본사이클(정점)인가?
(1) 인접행렬 (Adjacent Matrix)
그래프 G = (V, E)에서 IVI = n일때 G의 인접행렬은 n * n 행렬 A로 나타내어지며, 이때 A의 각 원소 aij는 다음과 같이 정의됨
aij = 1 (if (vi, vj) ∈ E), 0 (otherwise)
(i와 j 사이에 연결선이 있으면 1, 없으면 0)
예제 7-3. 다음 그래프의 인접행렬을 구해라
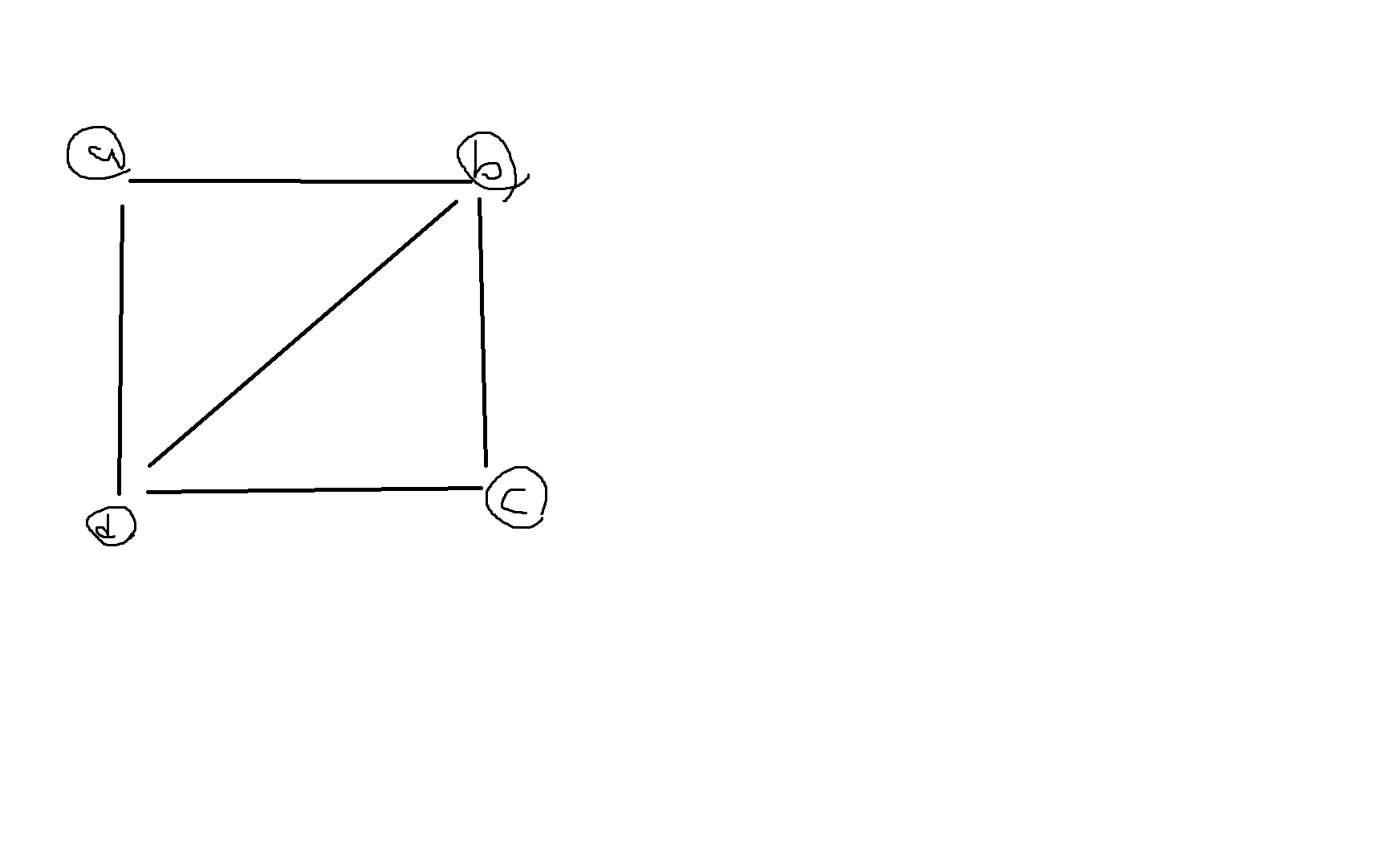
| a | b | c | d | |
|---|---|---|---|---|
| a | 0 | 1 | 0 | 1 |
| b | 1 | 0 | 1 | 1 |
| c | 0 | 1 | 0 | 1 |
| d | 1 | 1 | 1 | 0 |
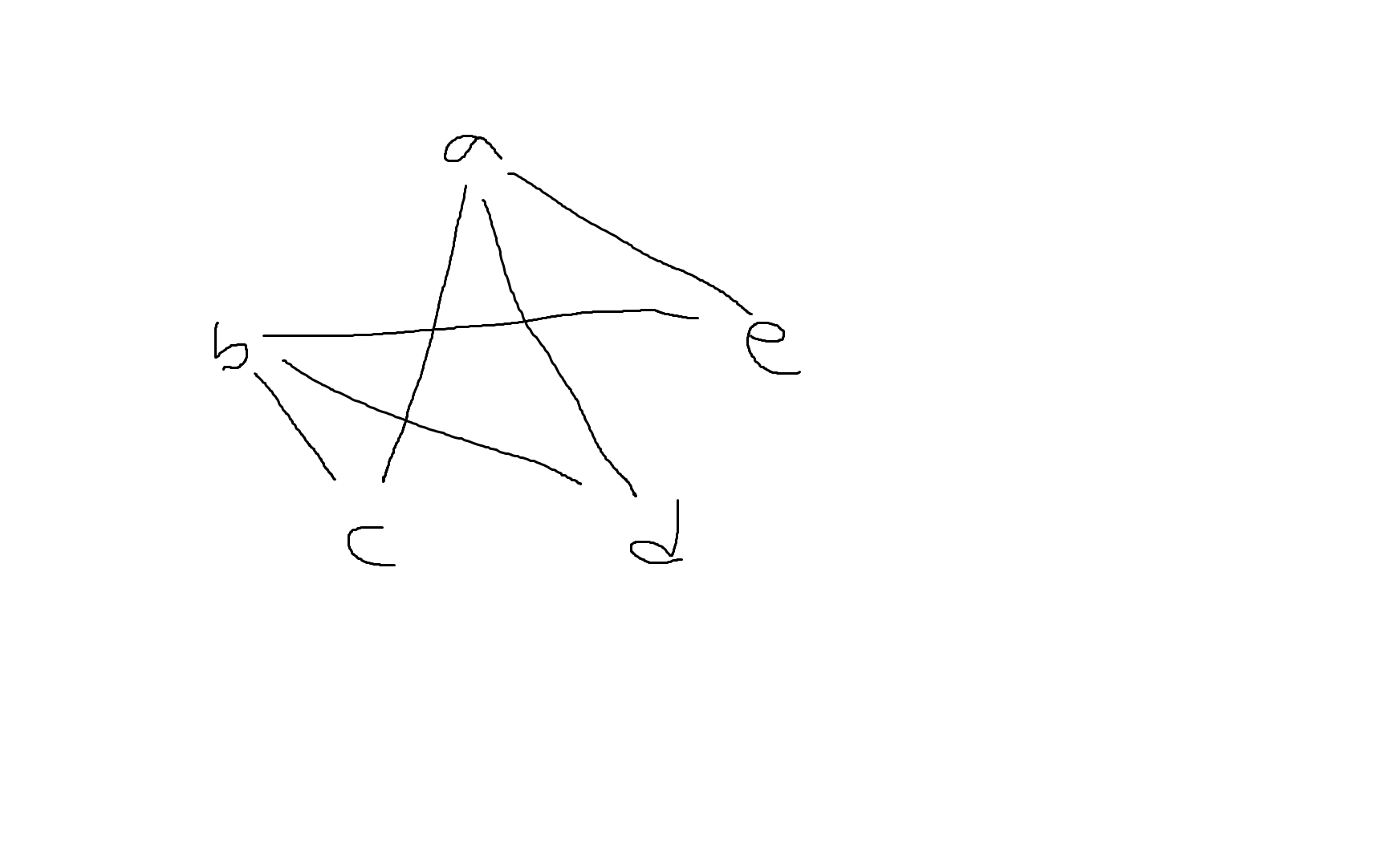
예제 7-4. 다음과 같은 인접행렬을 가지는 그래프를 그려보자
| a | b | c | d | e | |
|---|---|---|---|---|---|
| a | 0 | 0 | 1 | 1 | 1 |
| b | 0 | 0 | 1 | 1 | 1 |
| c | 1 | 1 | 0 | 0 | 0 |
| d | 1 | 1 | 0 | 0 | 0 |
| e | 1 | 1 | 0 | 0 | 0 |
(2) 인접리스트 (Adjacency List)
-
각 정점에 대해 포인터(Pointer)가 주어지고, 그 점으로부터 연결된 정점들을 차례로 연결리스트로 표시함
-
같은 리스트 내에서는 순서에 관계가 없음
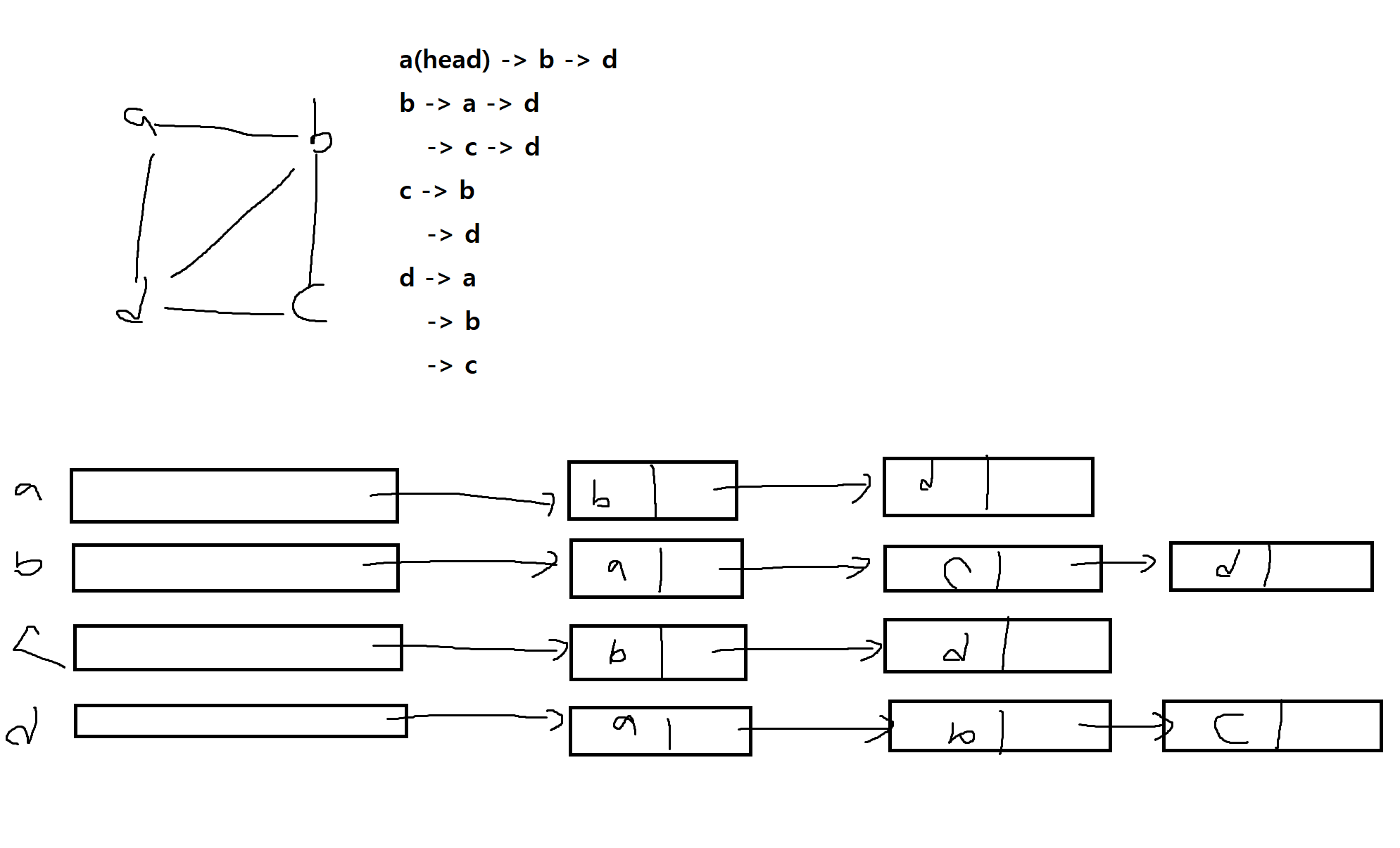
예제 7-5. 다음의 방향 그래프에서 인접 리스트를 구해보자.
정의 2-10. 오일러의 성질을 만족하는 특수한 형태의 그래프인 오일러 경로가 오일러순회를 다음과 같이 정의된다.
(1) 오일러 경로란 그래프에서 각 연결선을 단 한번씩만 통과하는 경로를 말한다.
(2) 오일러 순회란 그래프에서 꼭지점은 여러번 지날 수 있지만, 각 연결선은 단 한번만 통과하는 순회를 말한다.
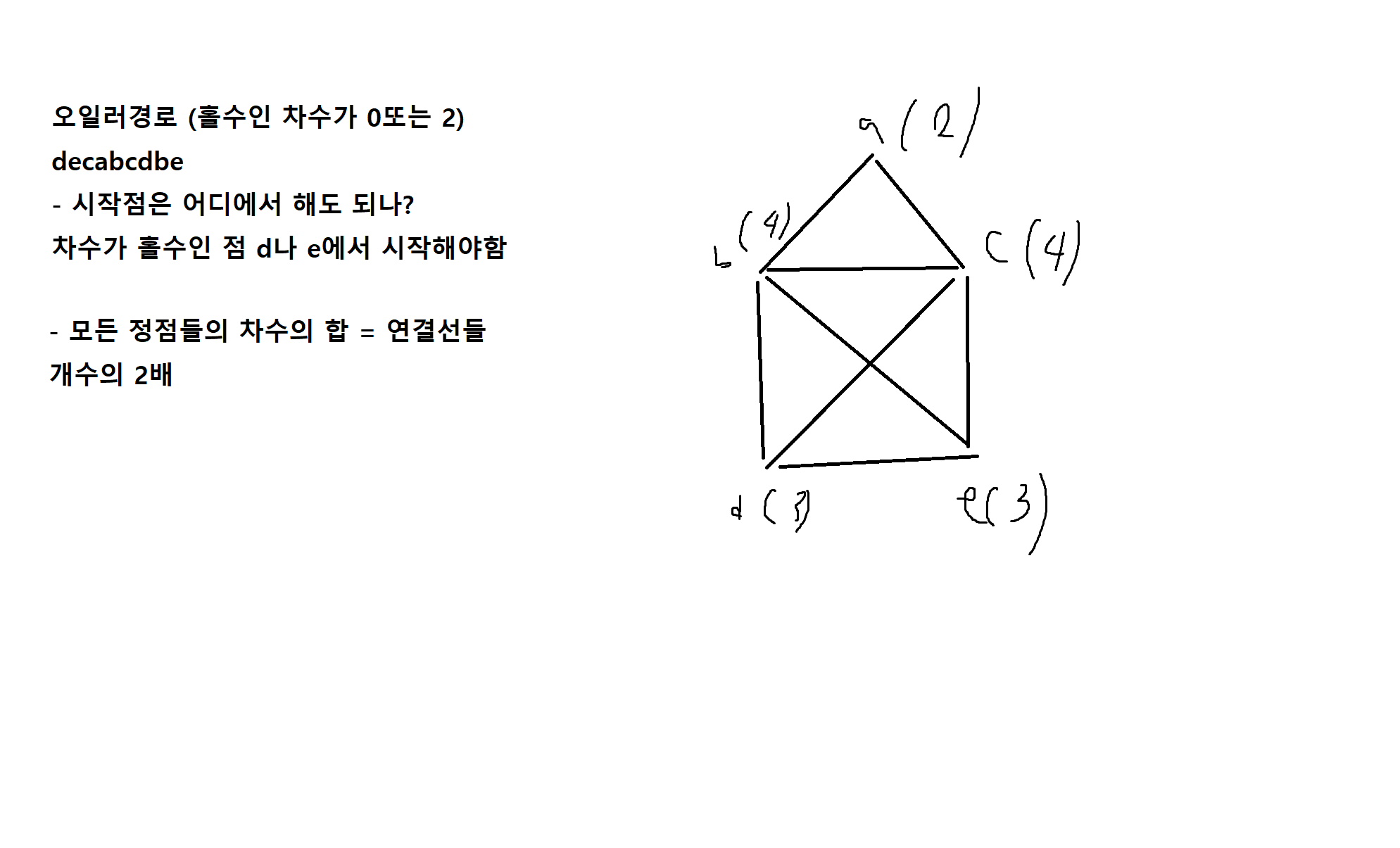
예제 7-6. 다음 그래프에서 모든 정점들의 차수의 합은 연결선들 개수의 2배임을 보여라.
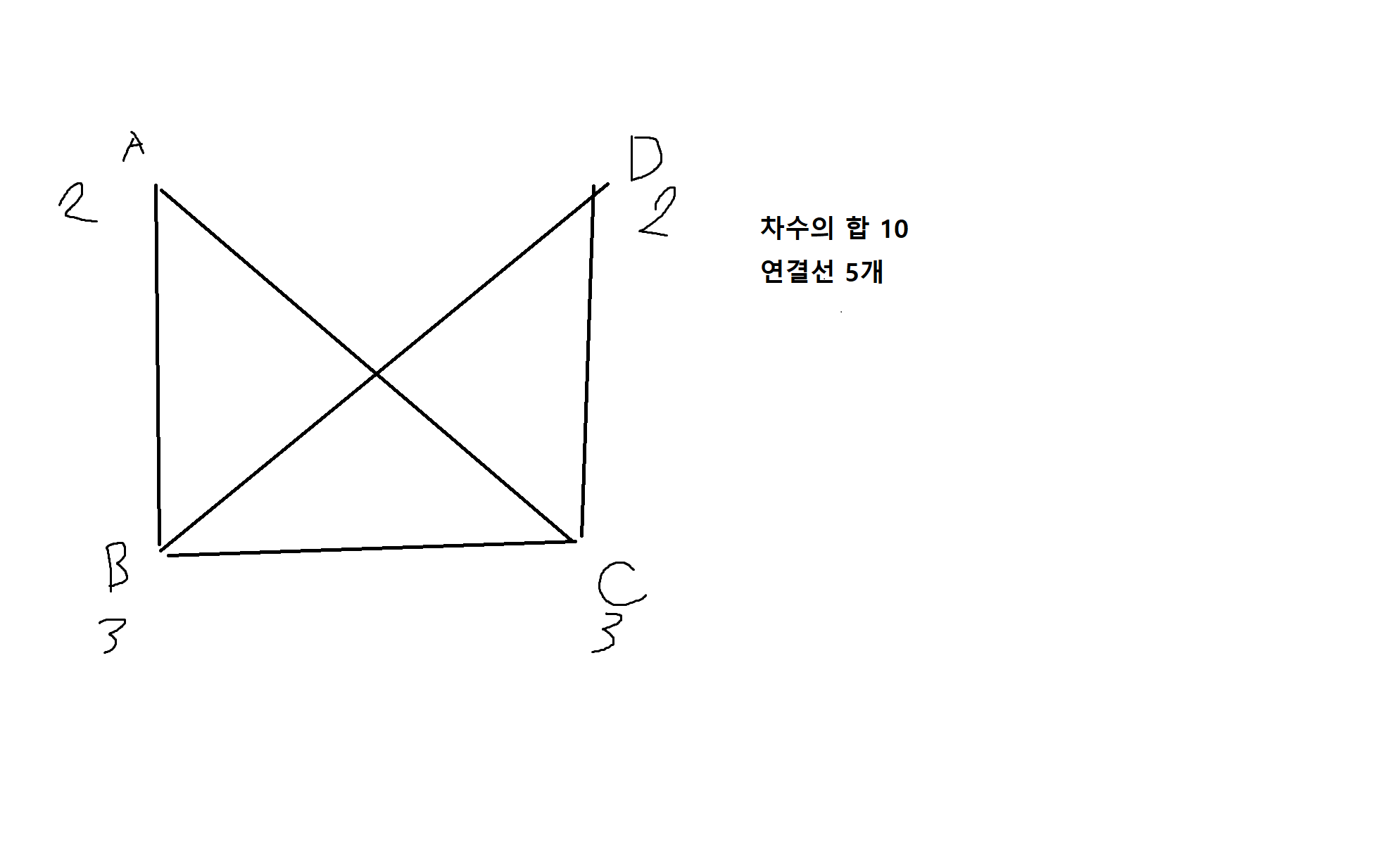
정의 7-2. 어떤 그래프 G가 오일러 경로를 가지기 위한 필요충분조건은 G가 연결그래프이고, 홀수차수의 개수가 0또는 2인 경우이다.
예제 7-7. 다음과 같은 두 그래프들이 오일러경로를 가지는지 확인해라
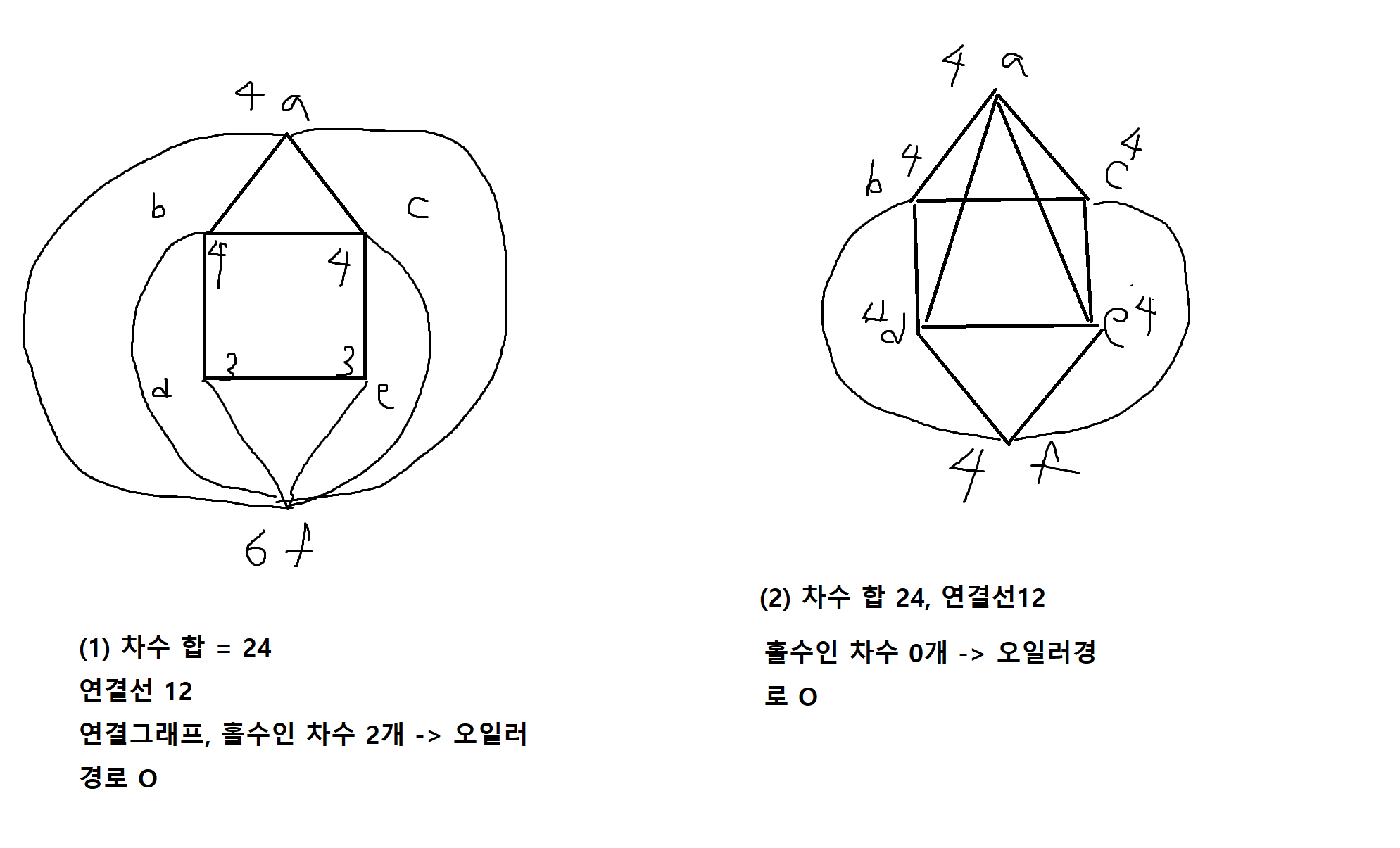
정의 2-3. 어떤 그래프 G가 오일러 순회를 가지기 위한 필요충분조건은 G가 연결그래프이고, 모든 정점들이 짝수 개의 차수를 가지는 경우이다.
예제 7-8. 다음 그래프가 오일러순회가 가능한지 판별해보자.
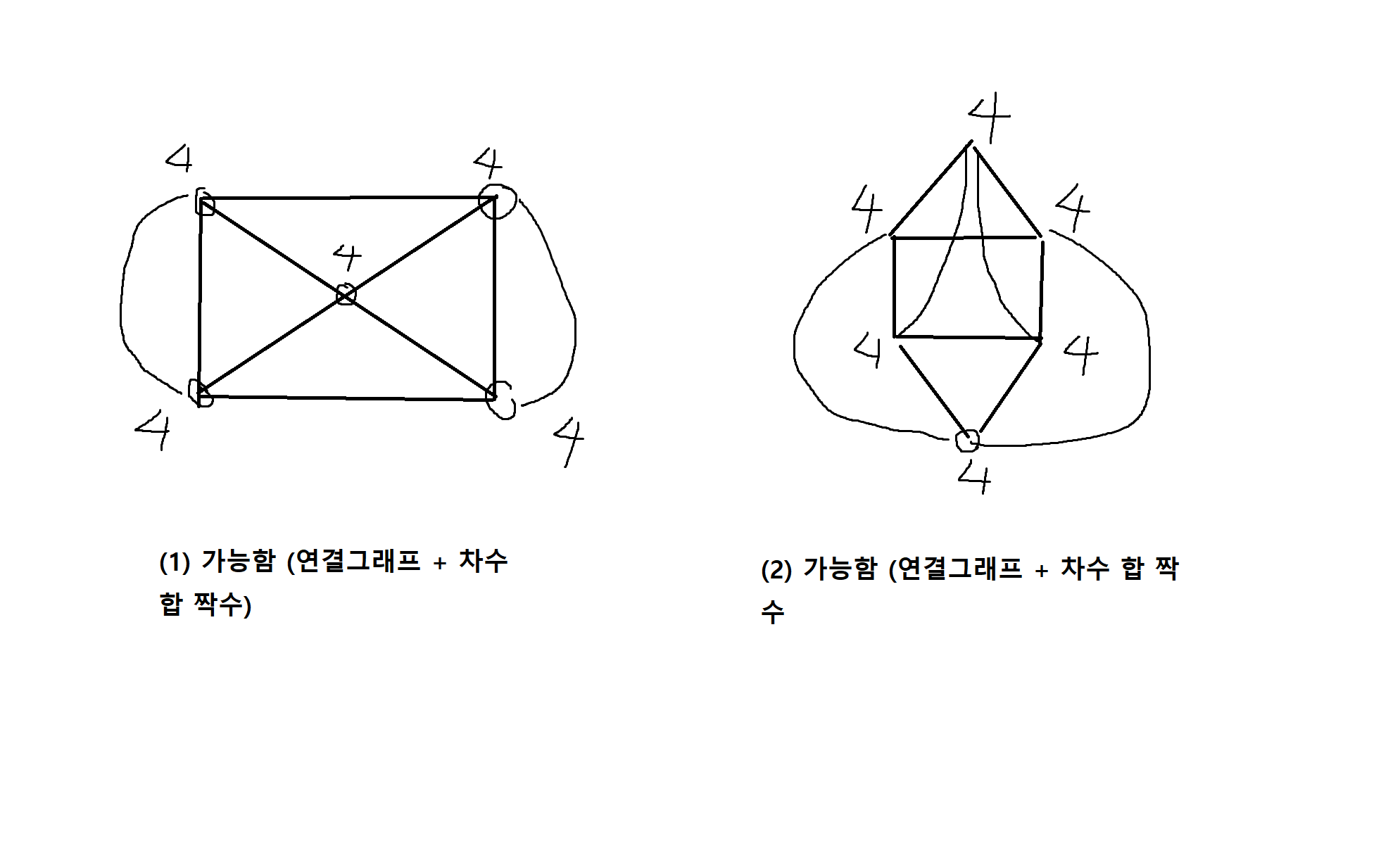
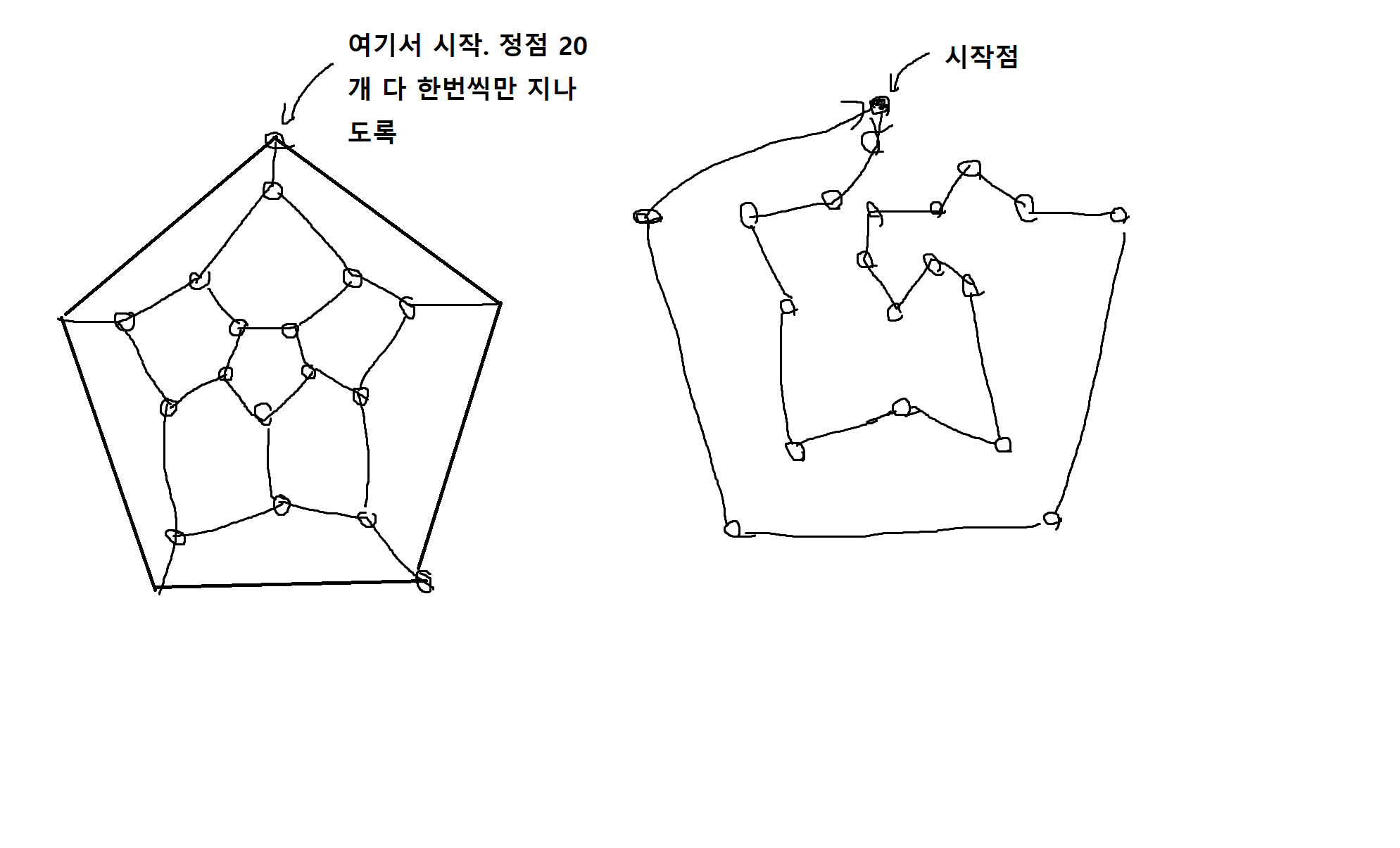
정의 7-12. 해밀턴의 성질을 만족하는 특수한 형태의 그래프인 해밀턴 경로와 해밀턴 순회는 다음과 같이 정의된다.
(1) 해밀턴 경로란 그래프에서 모든 꼭지점을 한번씩만 지나지만 시작점으로 돌아오지 않는 경로
(2) 해밀턴 순회란 그래프에서 모든 꼭지점들을 오직 한번씩만 지나는 순회(시작점으로 다시 돌아감)를 말함
예제 7-9) 다음 그래프에서 굵은 섹션으로 표현된 연결선을 해밀턴 순회를 나타냄을 알아봐라.
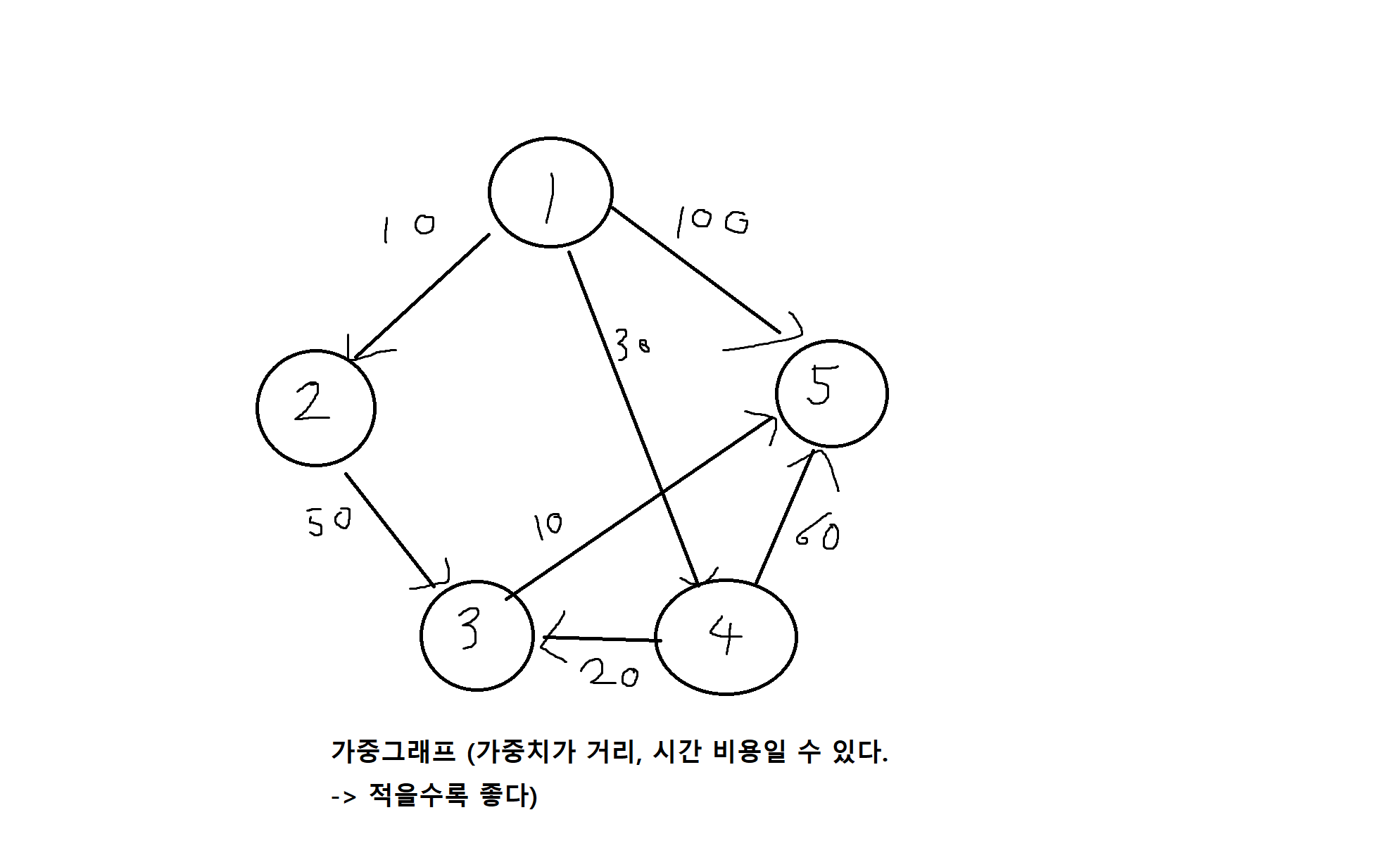
정의 7-13. 그래프 G와 각 연결선에 0보다 큰 수가 할당되었을 때 이 값을 가중값(weight)이라고 하며, 이와 같은 그래프를 가중그래프 (weight graph)라고 한다.
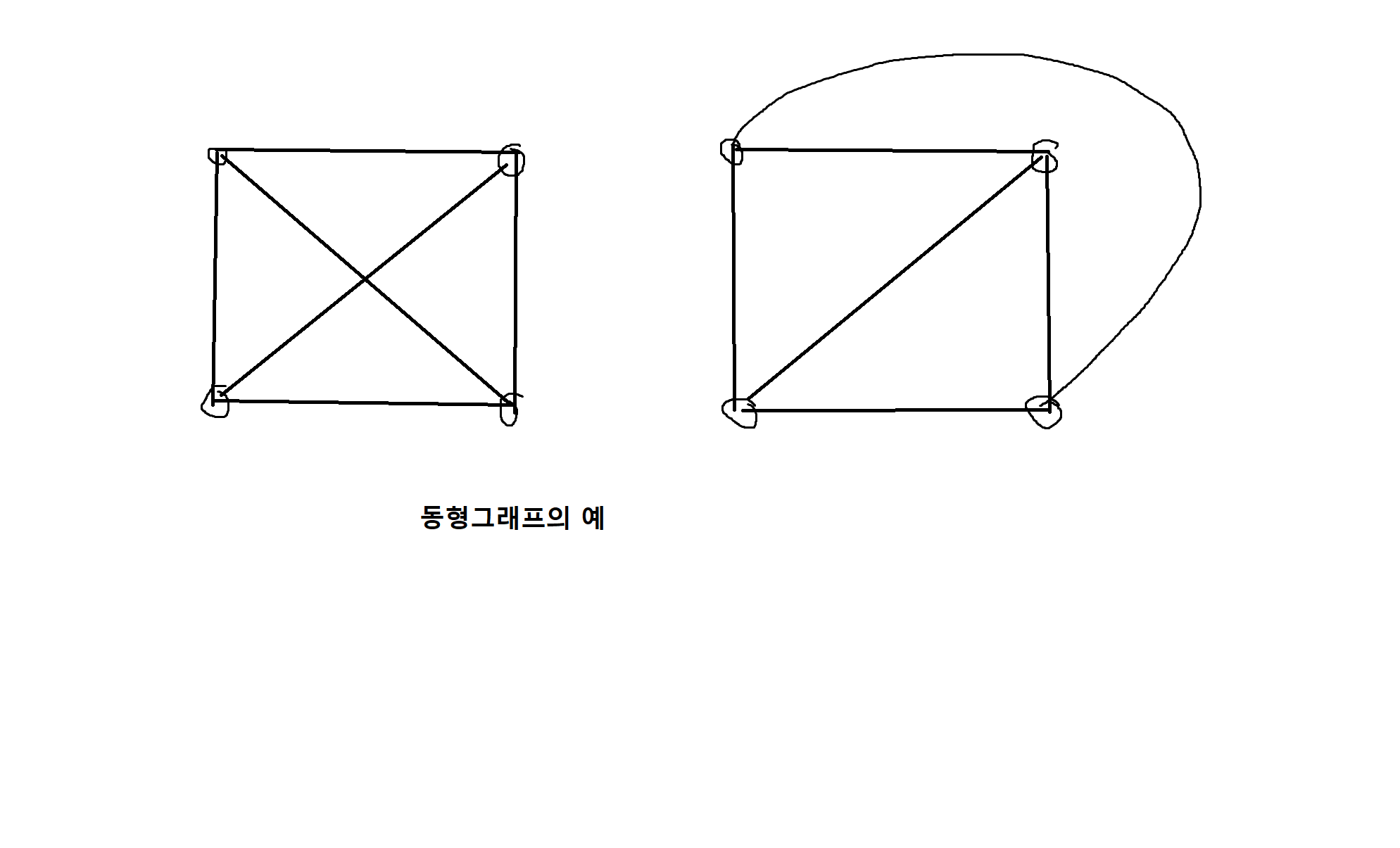
정의 7-14. 그래프 G₁= (V₁, E₁)과 G₂= (V₂, E₂)가 주어졌을 때, 전단사 함수 f: v₁-> v₂가 존재하며 (u, v) ∈ E₁↔ {f(u), f(v)} ⊂= E₂이면 이를 동행(ismorphism)이라고 하고 G과 G₂를 동형 그래프(isomorphic graph)라고 한다.
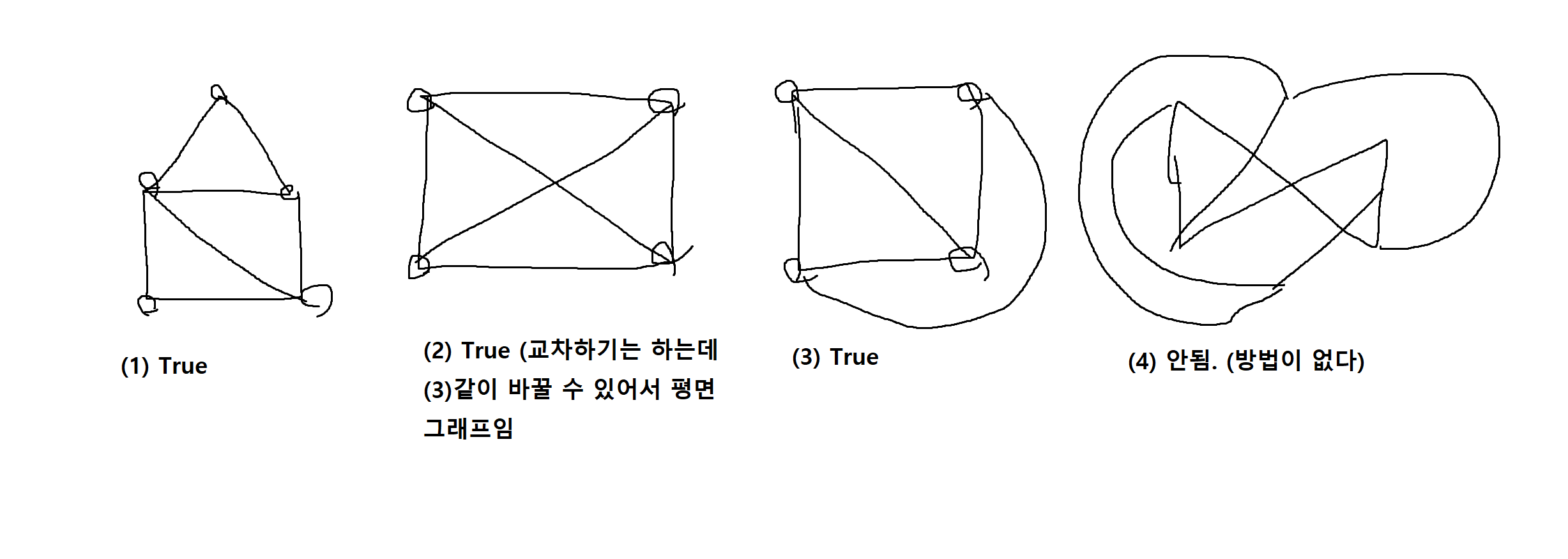
정의 7-15. 평면상에서 어떠한 연결선들도 서로 교차할 수 없도록 그려진 하나의 그래프를 평면그래프(planer graph)라고 한다.
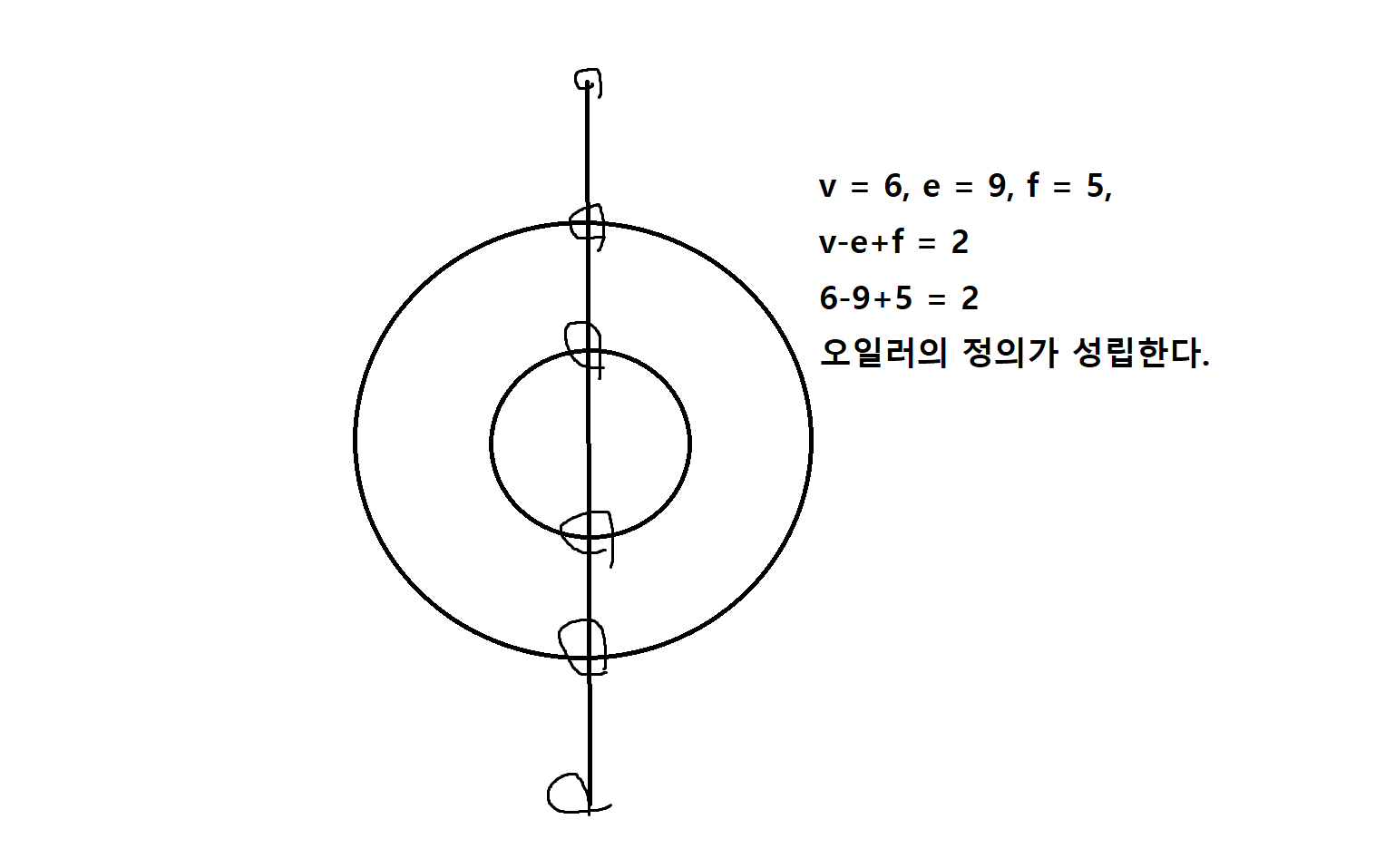
정의 7-4. 연결된 평명 그래프에서 꼭지점의 수를 v, 연결선의 수를 e, 면의 수를 f라고 할때 v-e+f = 2이다. (오일러의 정리)
예제 7-11. 다음 그래프에서 오일러의 정리가 성립하는지 살펴보자.
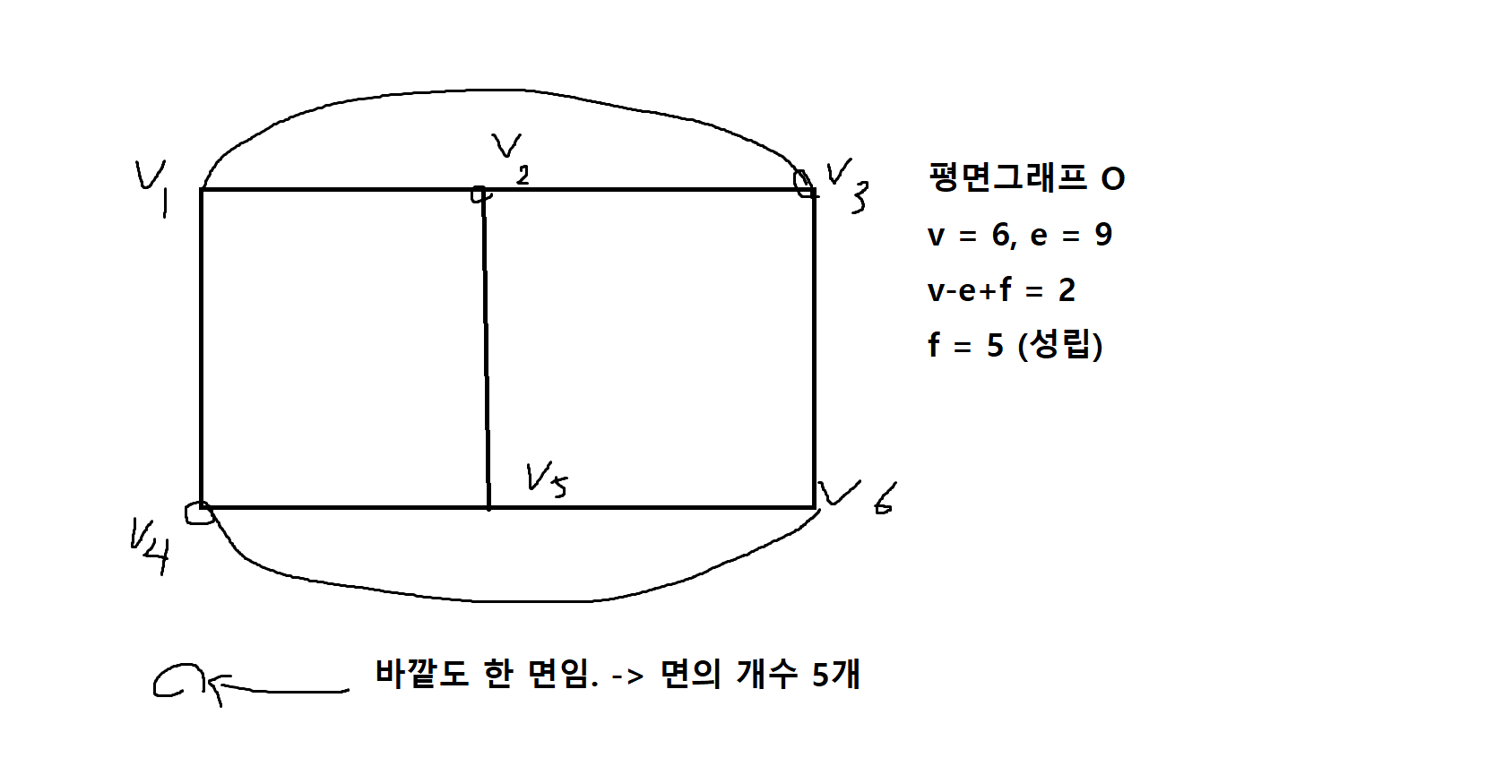
예제 7-12. 다음 그래프에서 오일러의 정리가 성립하는지 살펴보자.
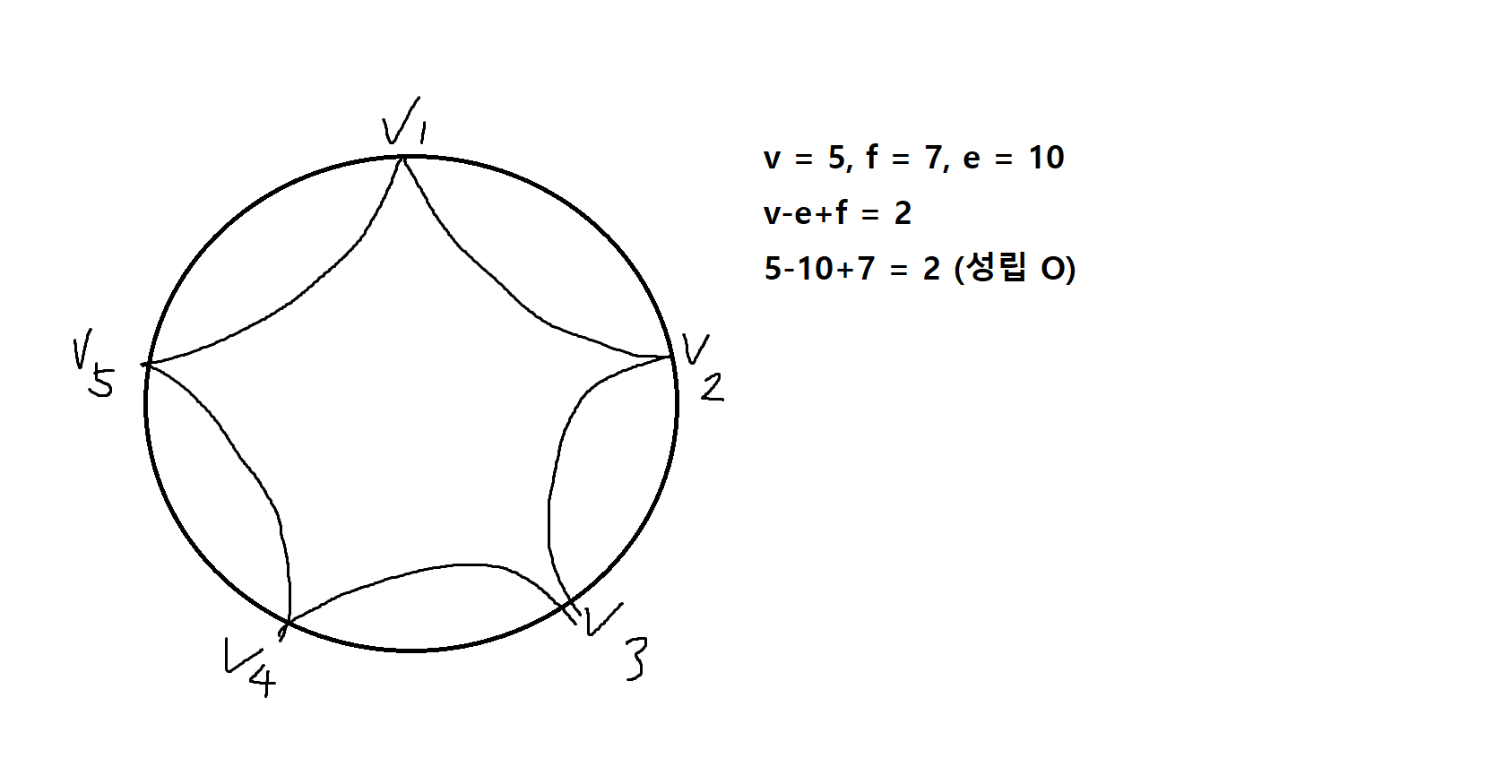
연습문제
1) 다음 그래프의 인접행렬을 구하시오.
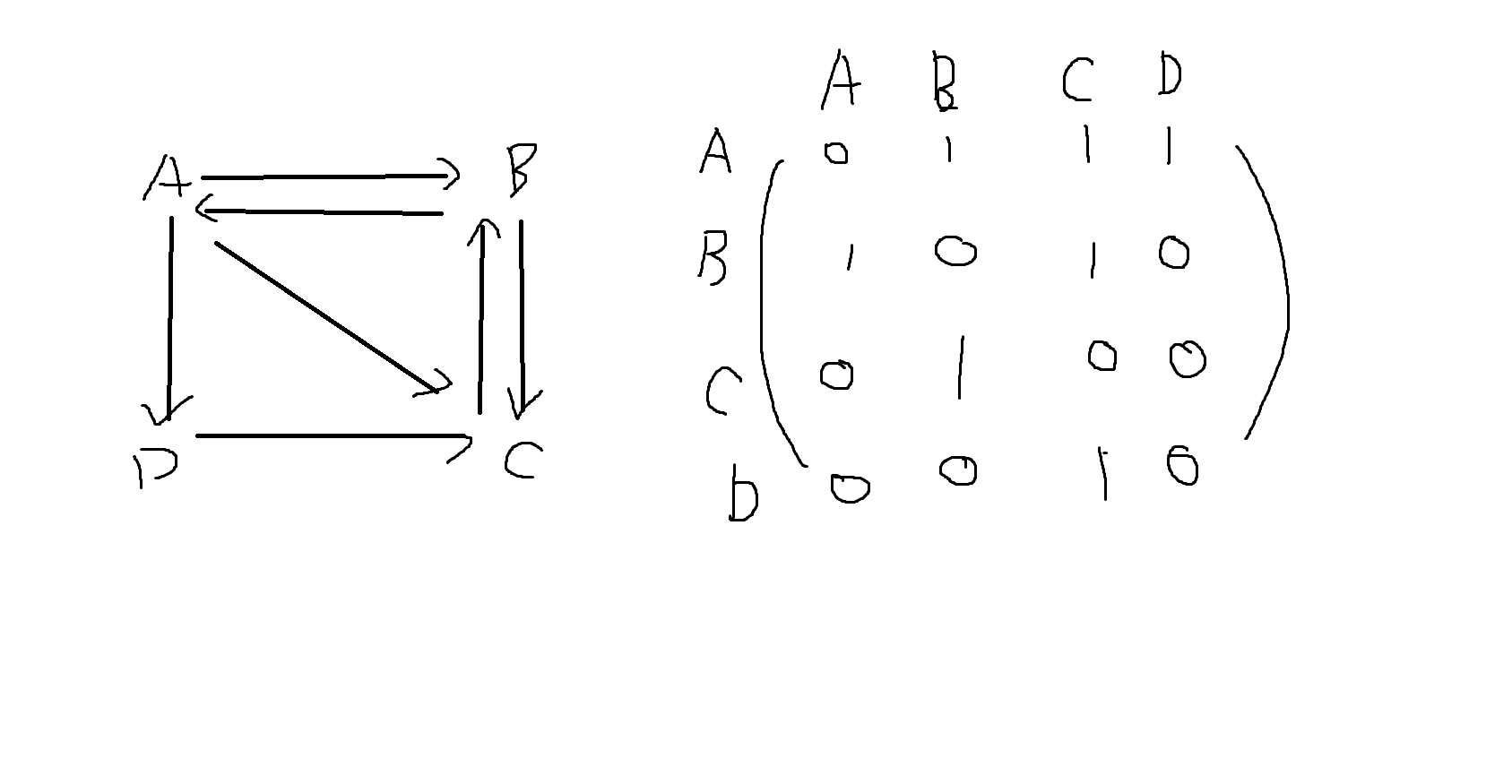
2) 다음 그래프의 인접행렬을 구하시오
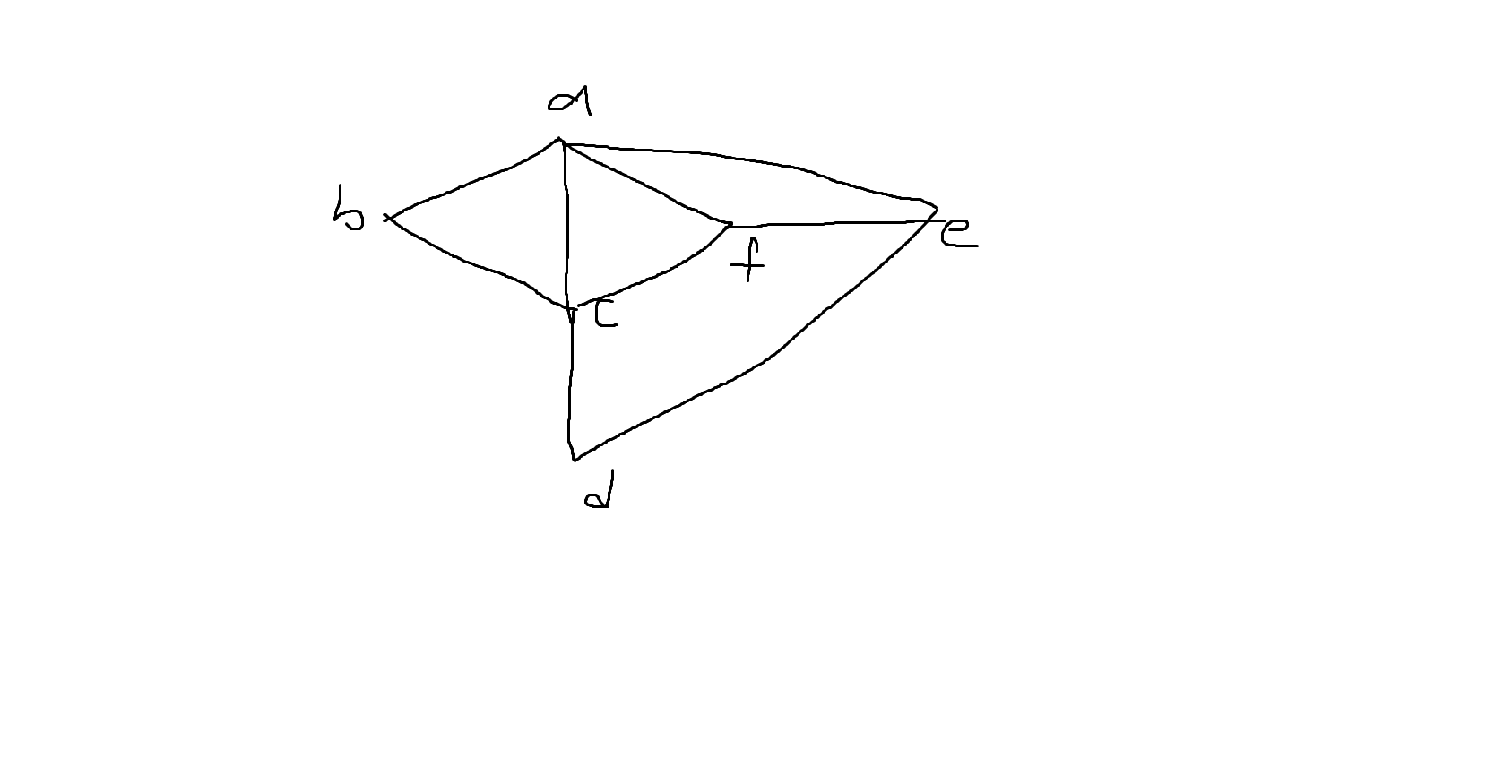
| a | b | c | d | e | f | |
|---|---|---|---|---|---|---|
| a | 0 | 1 | 1 | 0 | 1 | 1 |
| b | 1 | 0 | 1 | 0 | 0 | 0 |
| c | 1 | 1 | 0 | 1 | 0 | 1 |
| d | 0 | 0 | 1 | 0 | 1 | 0 |
| e | 1 | 0 | 0 | 1 | 0 | 1 |
| f | 1 | 0 | 1 | 0 | 1 | 0 |
3) 다음 그림이 오일러 순회(연결그래프이고 모든 차수가 짝수)를 가지는지 판별하고 오일러순회(모든 연결선 한번씩 가서 돌아옴)를 나타내어라
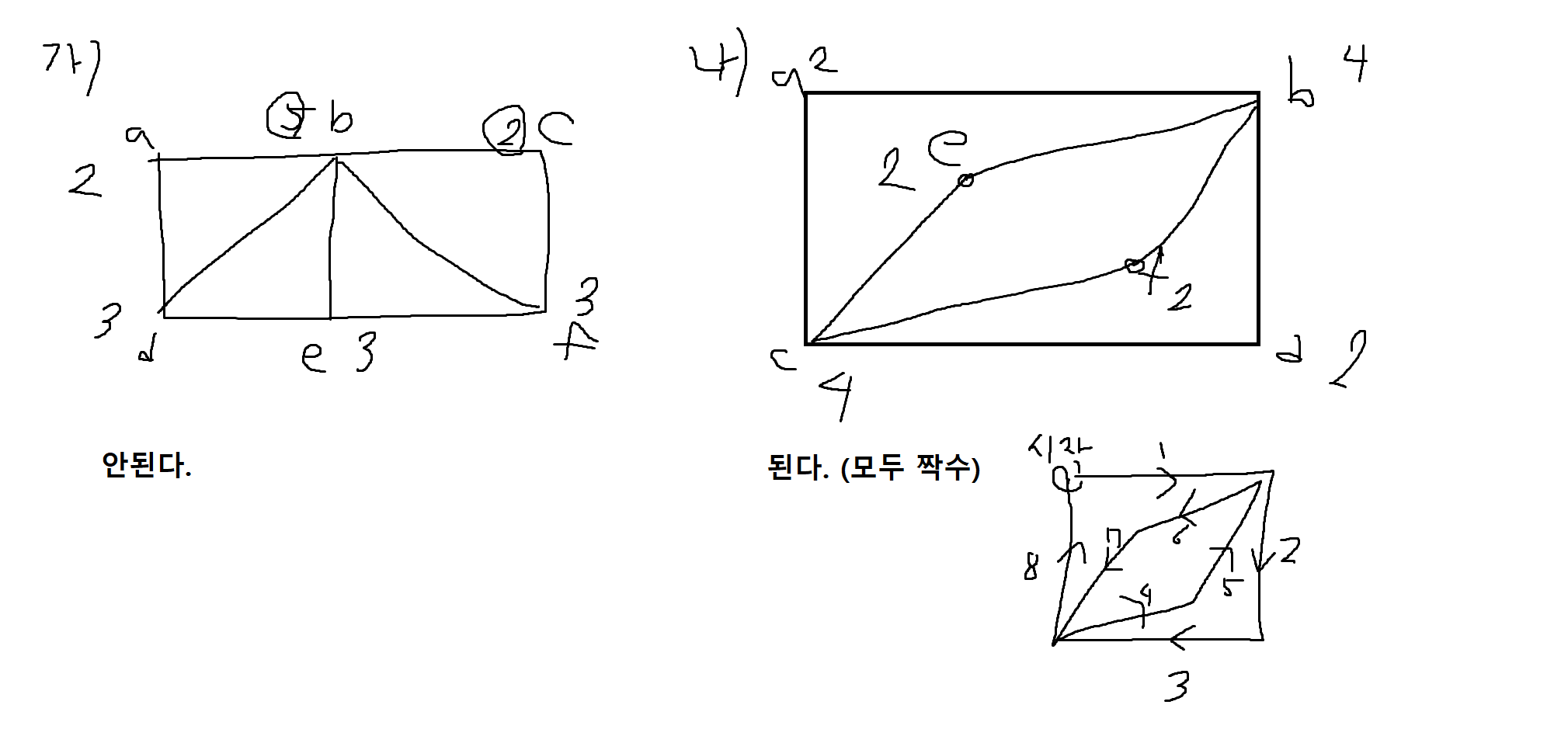
4) 다음 그림이 해밀턴 순회를 가지는지 판별해보시오
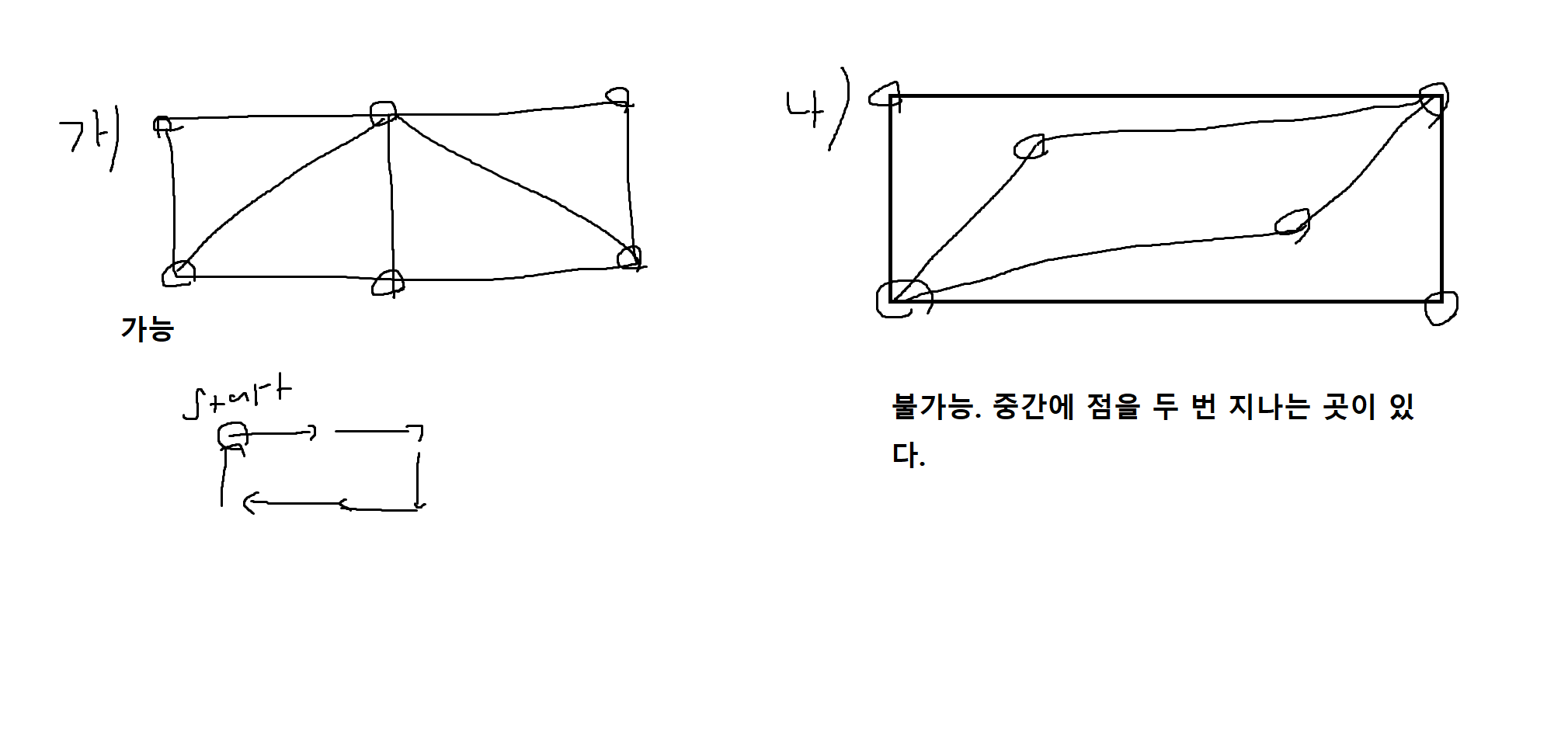
5) 다음의 그래프에서 오일러의 정리가 성립함을 보이시오.
오일러의 정리 (v-e+f = 2)
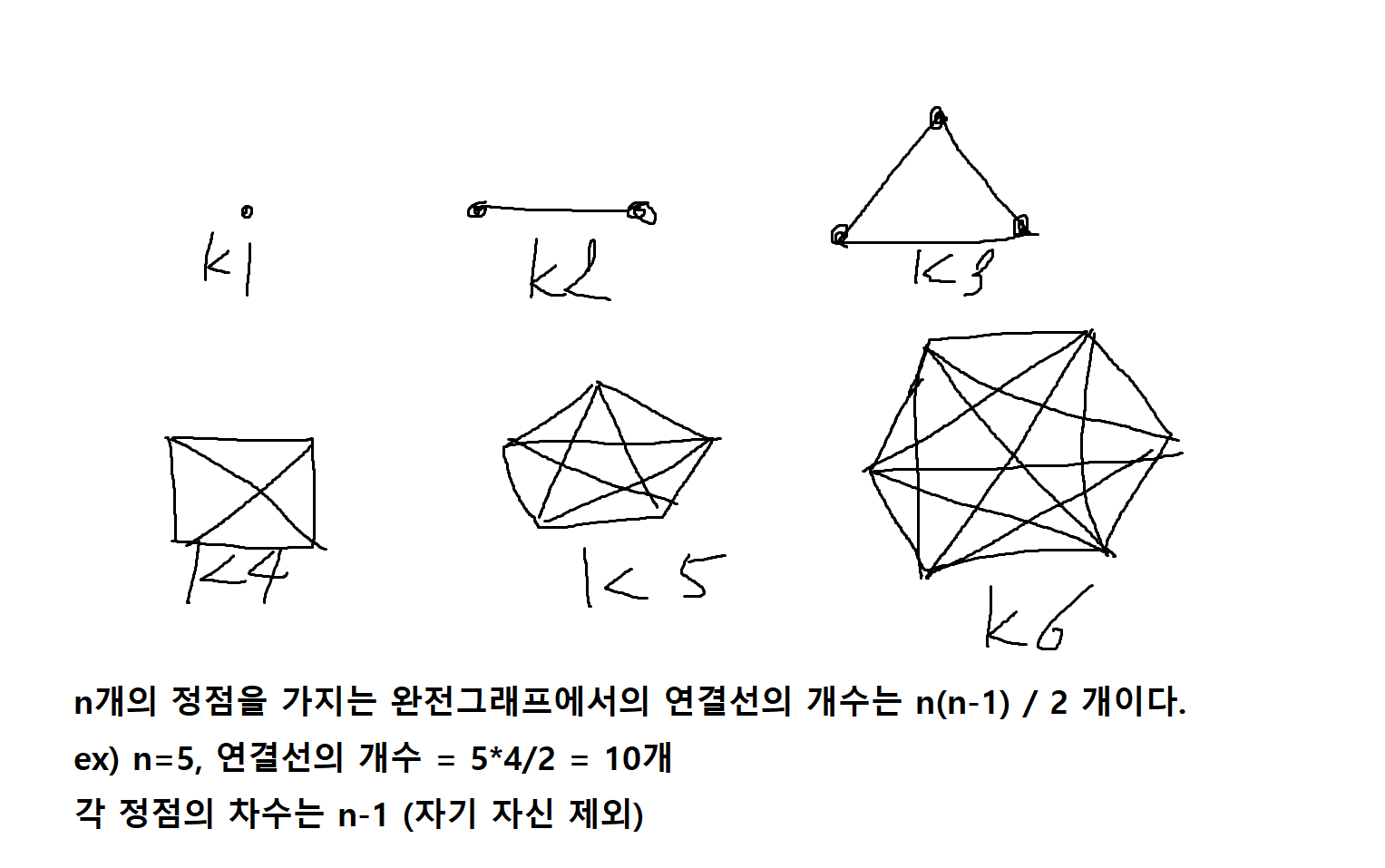
정의 7-16. 그래프 G = (V,E)의 모든 정점들의 쌍 사이에 연결선이 존재하면 G를 완전그래프라고 한다. 즉, 각 꼭지점이 다른 꼭지점들과 연결되는 그래프를 말하는데, n개의 꼭지점으로 구성된 완전그래프는 Kn으로 표기한다.
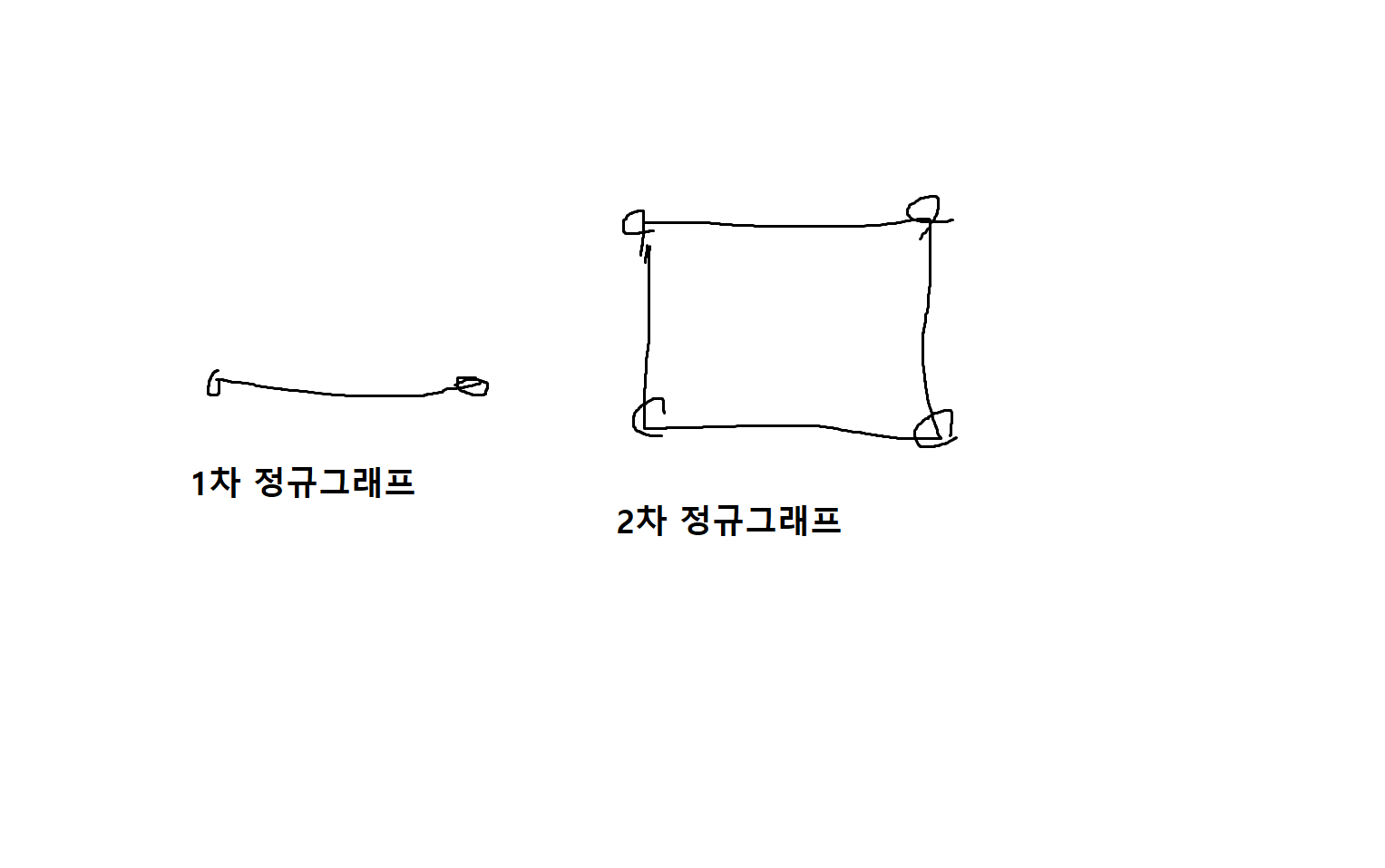
정의 7-17. 그래프 G = (V, E)의 모든 꼭지점의 차수가 k이면 G를 K차 정규그래프라고 한다.
정의 7-18.
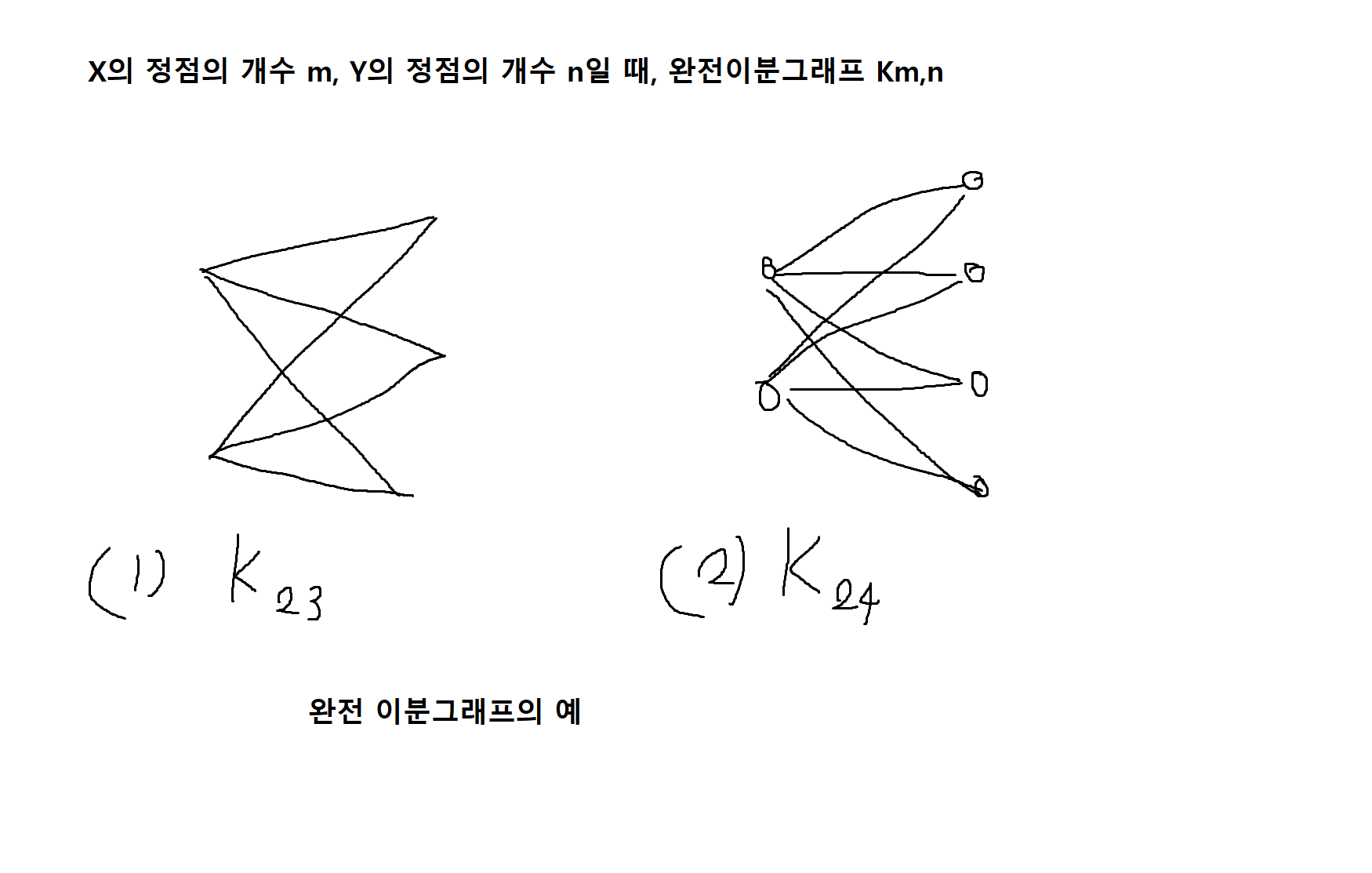
그래프 G = (V, E)에서 V(전체 정점 개수)가 두 부분집합 X와 Y = V - X로 나누어져 각 연결선이 X내의 정점과 Y내의 정점의 쌍으로 연결되면 그래프 G를 이분그래프(bipartite graph)라고 한다. 이때 X내의 모든 정점들과 Y내의 모든 정점들 사이에 연결선이 존재하면 G를 완전 이분그래프(complete bipartite graph)라고 한다.
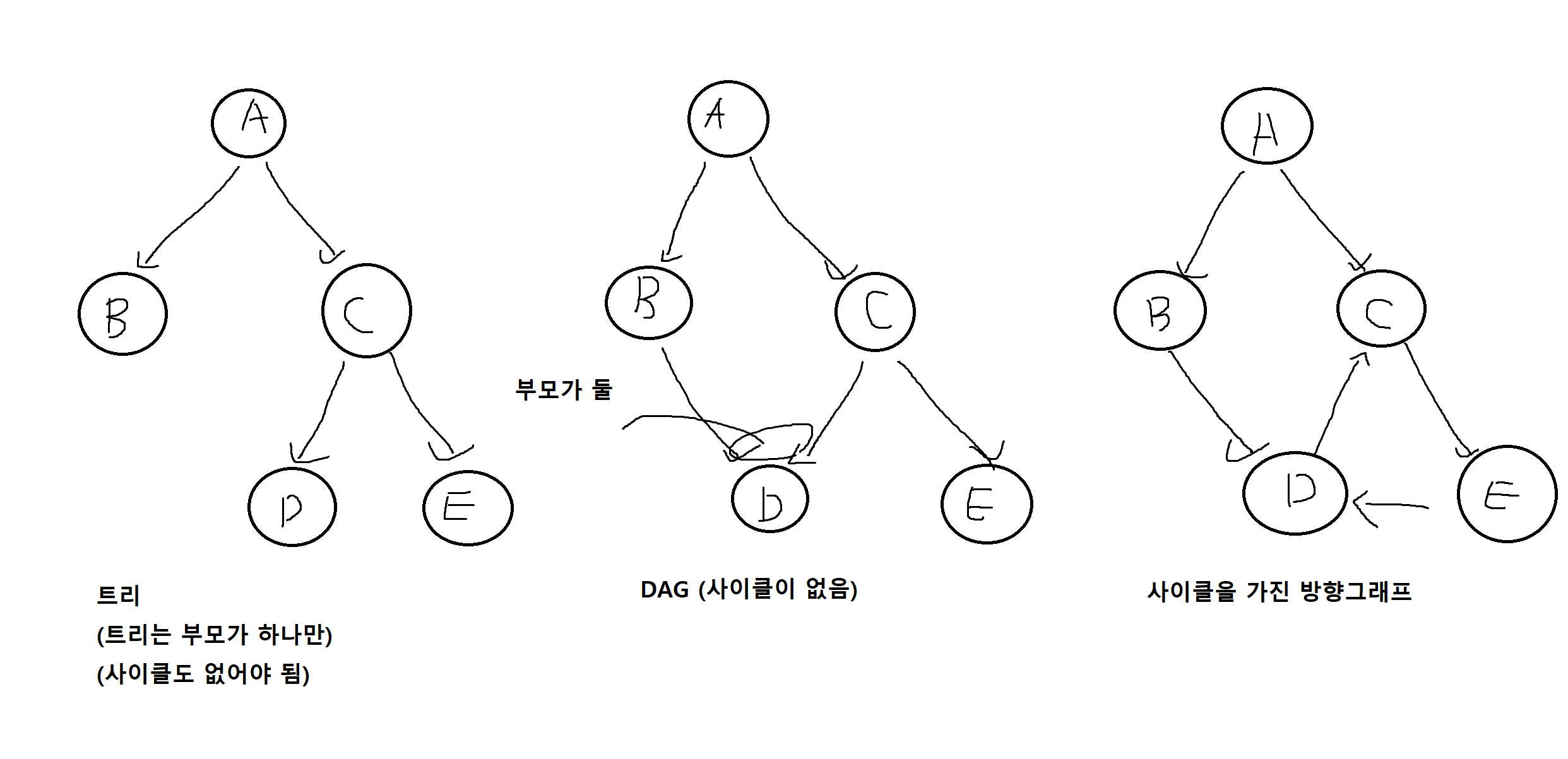
정의 7-19. 방향 비사이클 그래프 (Directed Acycle Graph : DAG)는 사이클이 없는 방향그래프를 말하는데, 트리보다는 일반적이나 임의의 방향그래프보다는 제한적이다.
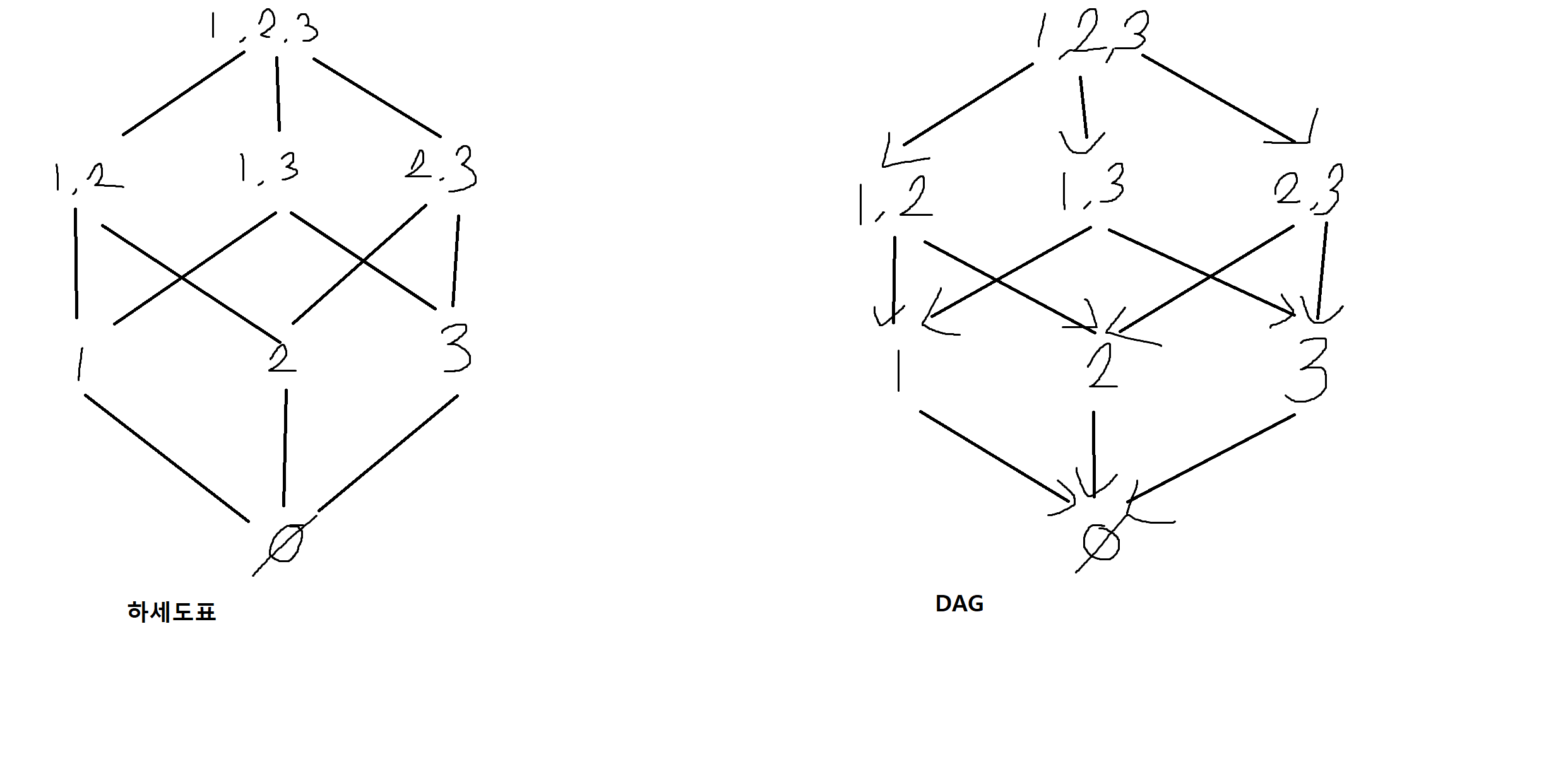
예제 7-13. 집합 {1,2,3}의 진부분집합을 DAG로 표현해보자.
DAG - 방향이 있고 사이클은 없고.
-
DAG는 시스템 흐름도, 컴파일러에서의 최적화 등 많은 분야에서 폭넓게 쓰이고 있다.
-
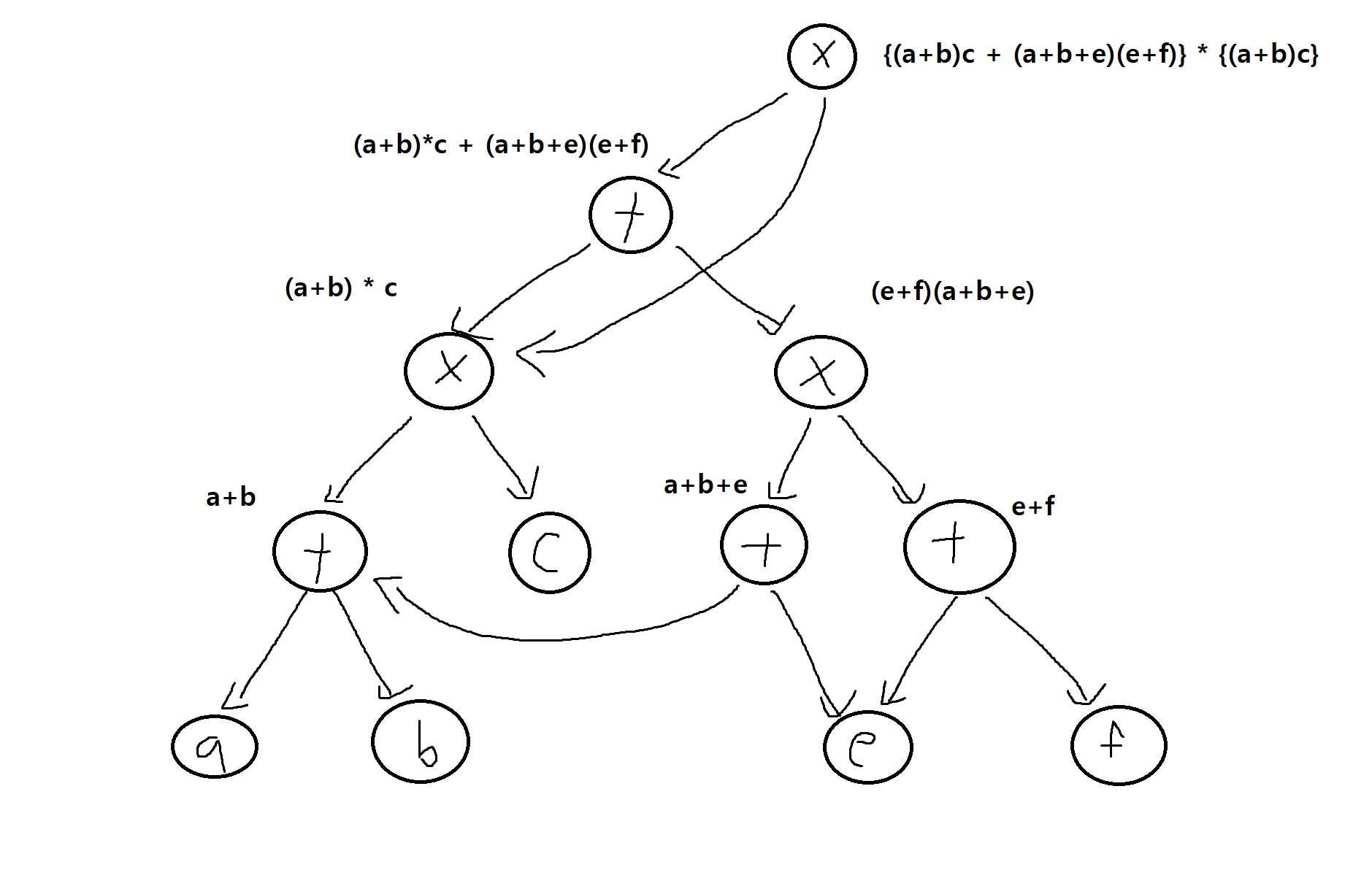
또한 공통인수를 가진 산술적 표현의 구조를 나타내는데 있어서도 매우 유용하다.
-
예를 들어 {(a+b) c + ((a+b)+e) (e+f)} {(a+b) c}에 있어서 a+b와 {(a+b) c}에 있어서 a+b와 (a+b) c는 공통으로 쓰이기 때문에 그림과 같이 DAG로 중복되는 것을 줄이고 간단히 표현할 수 있다.