트리
- 그래프의 특별한 형태로서 컴퓨터를 통한 자료처리와 응용에 있어서 매우 중요한 역할을 담당
- 이진트리에 경우에는 산술적 표현이나 자료구조 등을 매우 간단하게 표현할 수 있다는 장점이 있음
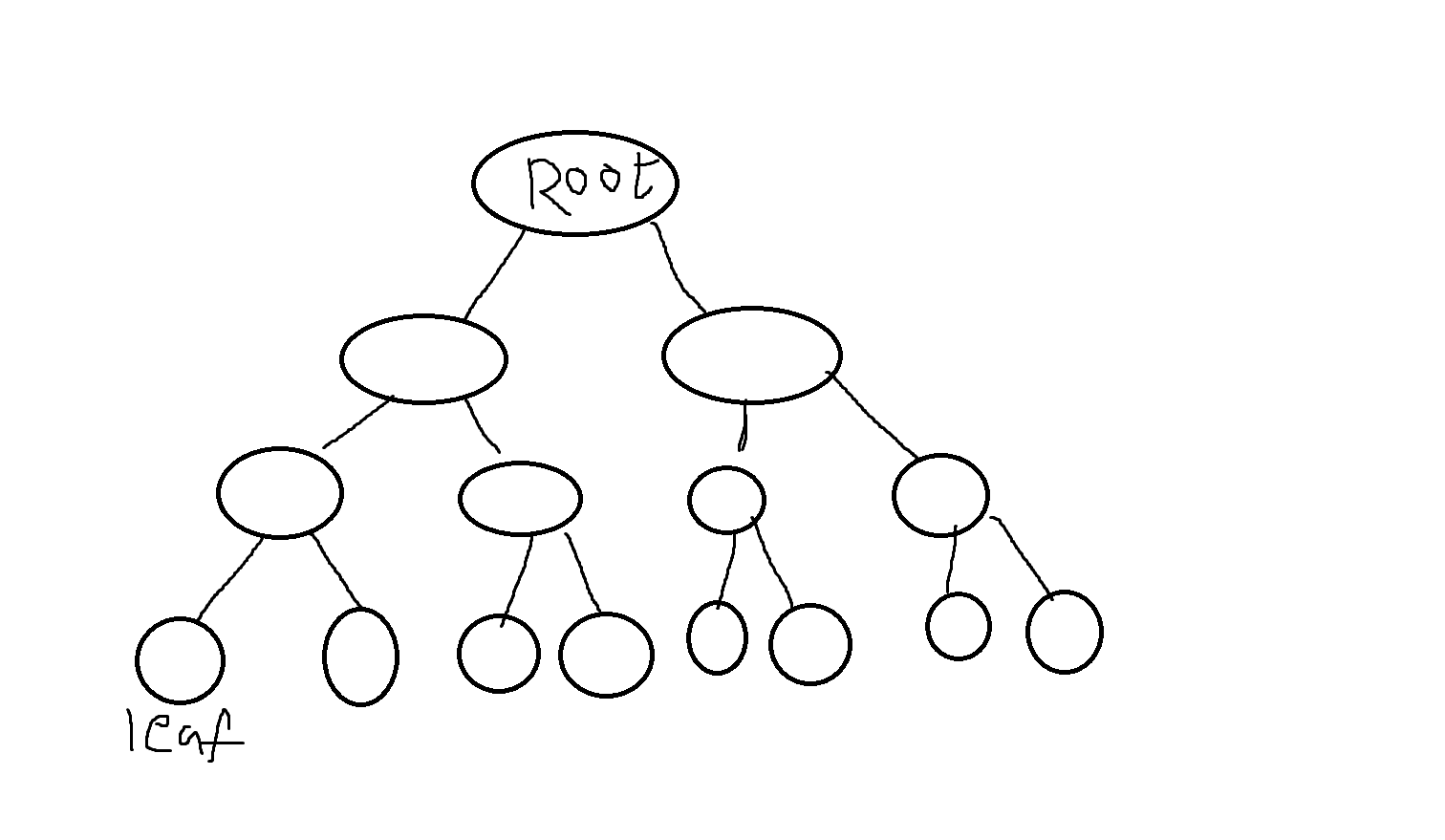
정의 8-1. 트리는 하나이상의 노드(node)로 구성된 유한집합으로서 다음의 2가지 조건을 만족한다.
(1) 특별히 지정된 노드인 Root(루트)가 있고,
(2) 나머지 노드들을 다시 각각 트리이면서 연결되지 않는 T₁,T₂,T₃...Tn (N>=0)으로 나누어진다. 이때 T₁,T₂,T₃...Tn은 루트의 서브트리(subtree)라고 한다.
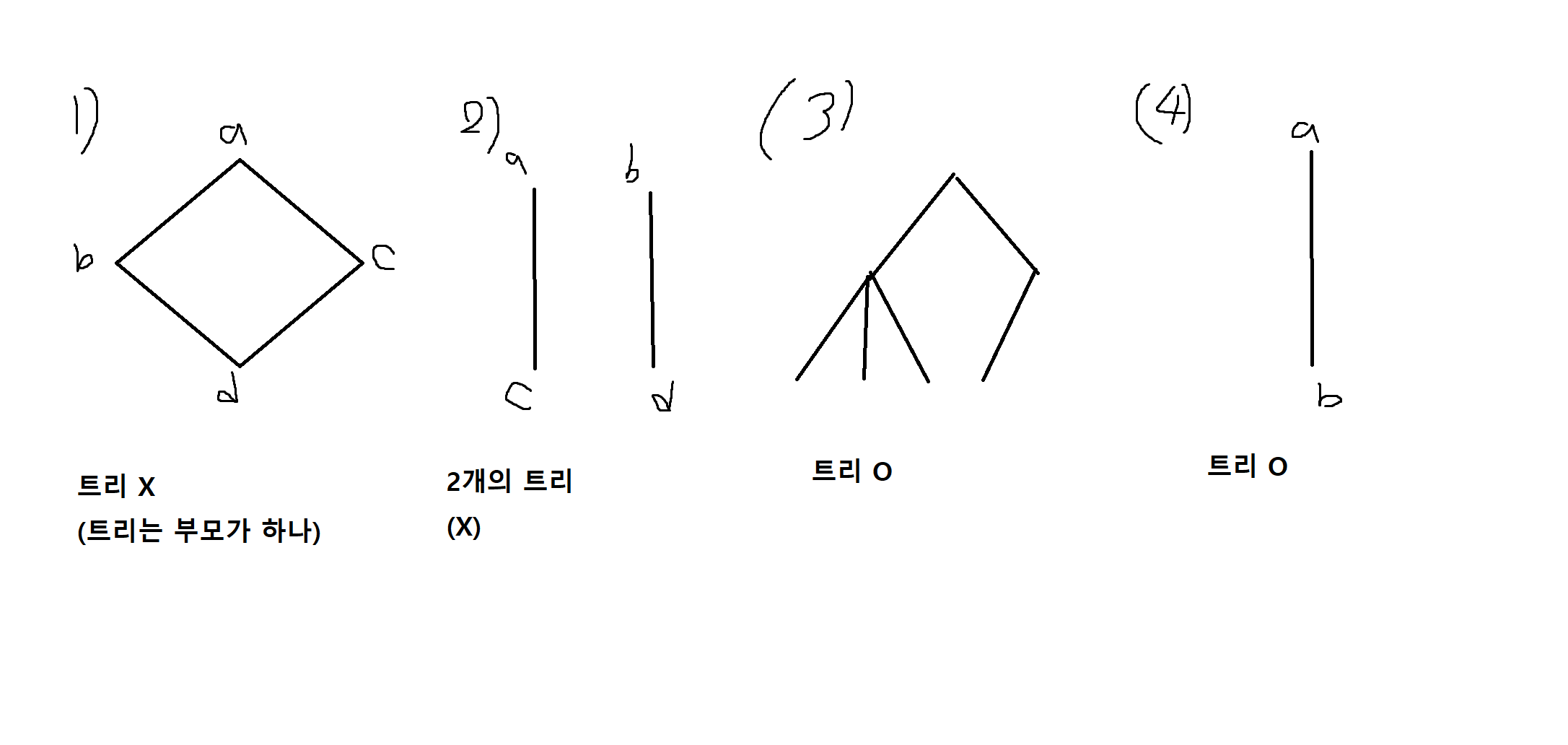
예제 8-1. 다음의 여러 그래프들이 트리에 해당하는지 판단해보자
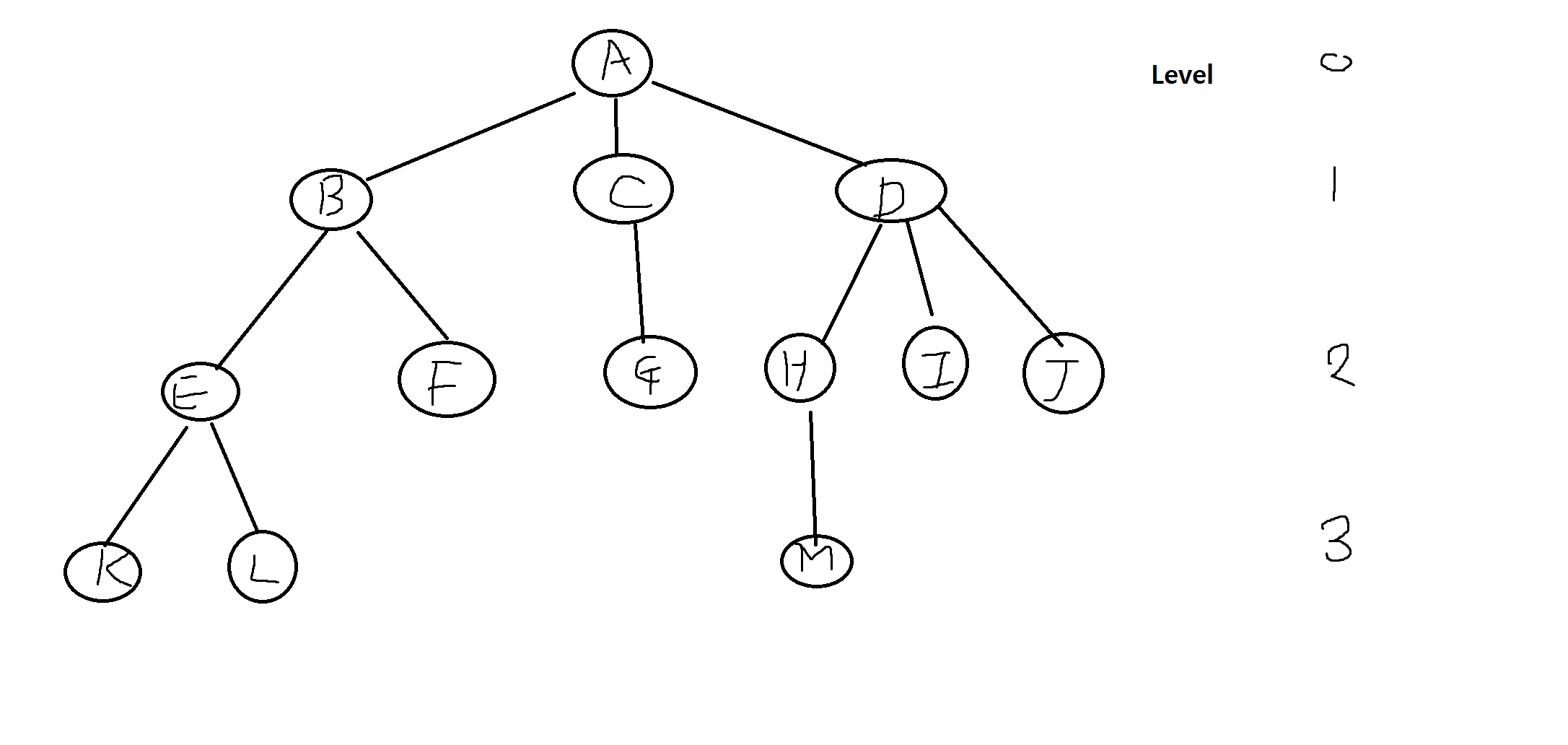
1) 루트 (root) : 주어진 그래프의 시작 노드로서 통상트리의 가장 높은 곳에 위치하며 노드 A가 루트노드임
2) 차수 (degree) : 어떤 노드의 차수는 그 노드의 서브트리의 개수를 나타내고, 노드 A의 차수는 3, B의 차수는 2, F의 차수는 0임
3) 잎노드 (leaf node) : 차수가 0인 노드로서 K,L,F,G,M,I,J가 잎노드에 해당함 (자식이 없을 때 차수가 0)
4) 자식노드 (children node) : 어떤 노드의 서브트리의 루트노드들을 말하는데 A의 자식노드는 B,C,D임
5) 부모노드 (parent node) : 자식노드의 반대개념으로서, B의 부모노드는 A이고, G의 부모노드는 C임
6) 형제노드 (sibling node) : 동일한 부모를 가진 노드. B,C,D는 모두 형제노드.
K,L도 형제, F,G는 아님
7) 중간노드 (internal node) : 루트도 아니고 잎노드도 아닌 노드
B,C,D,E,H 중간노드
8) 조상 (ancester) : 루트로부터 그 노드에 이르는 경로에 나타난 모든 노드. F의 조상은 B,A / M의 조상은 H,D,A
9) 자손 : 그 노드로부터 잎노드까지 경로상의 모든 노드
B의 자손 -> E, F, K, L
H의 자손 -> M
10) 레벨 (level) : 루트의 레벨을 0으로 놓고, 자손노드로 내려가면서 하나씩 증가
어떤 노드의 레벨이 p -> 자식 노드 레벨 p+1
11) 트리의 높이 (height) : 트리에서 노드가 가질 수 있는 최대 레벨로서 트리의 깊이(depth)라고 한다. 위 트리의 높이는 3
12) 숲 (forest) : 서로 연결되지 않는 트리들의 집합으로서 트리에서 루트를 제거하면 숲을 얻을 수 있음
예제 8-2. 다음 트리에서 주어진 물음에 답해보자
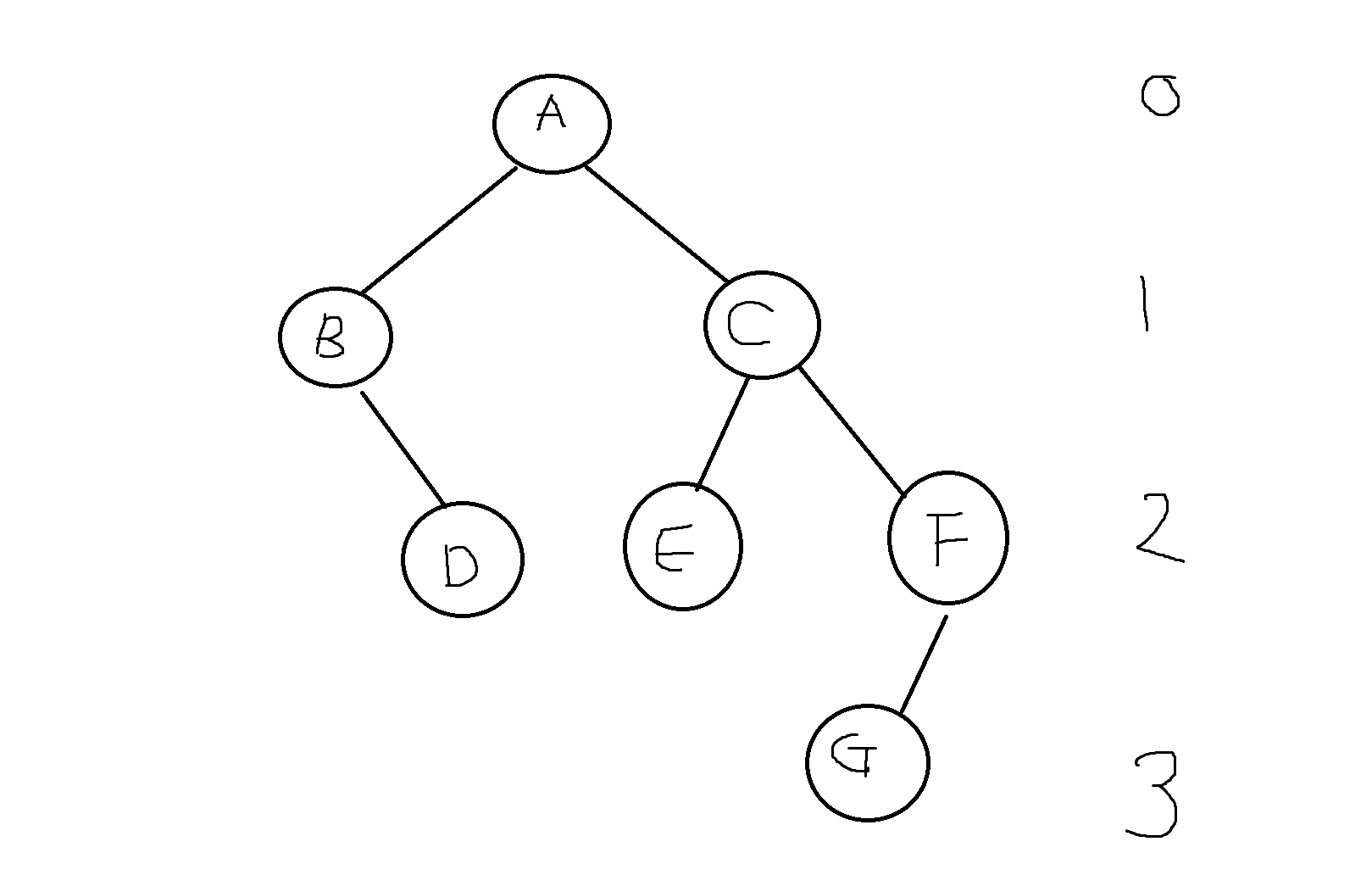
1) 잎노드 -> D, E, G
2) 트리의 높이 -> 3
3) C의 차수(자식이 2개) -> 2
4) G의 조상노드 -> F, C, A
정리 8-1. n개의 노드를 가진 트리는 n-1개의 연결선을 가진다.
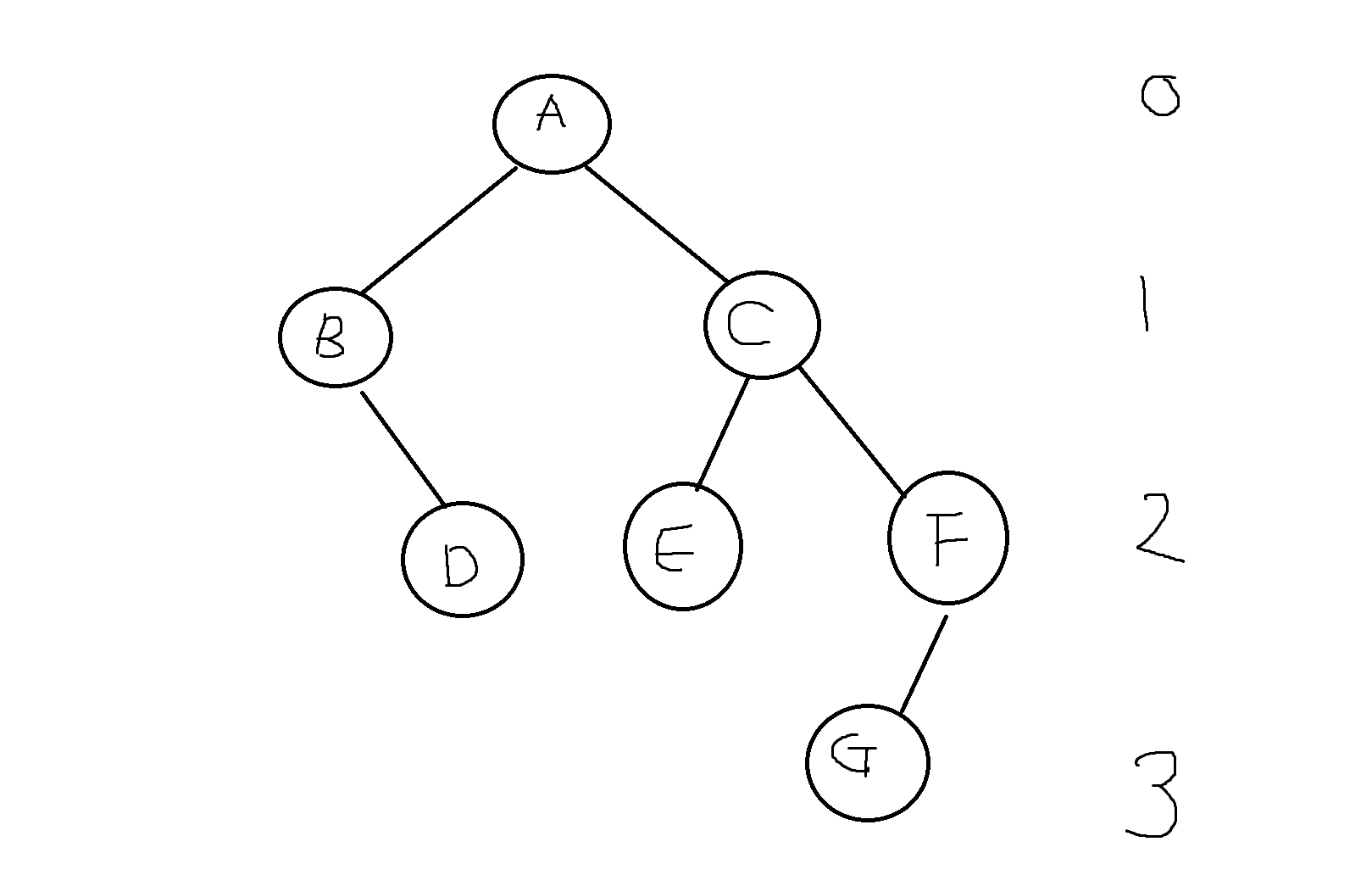
7개 노드 -> 6개의 연결선
15개 노드(정점) -> 14개의 연결선
그래프 G = (V, E)에서 |V| = n이고, |E| = m일 때 다음의 문장들은 모두 동치이다.
(1) G는 트리이다.
(2) G는 연결되어 있고 m = n-1이다.
(3) G는 연결되어 있고 어느 한 연결선만을 제거하더라도 G는 연결되지 않는다.
(4) G는 사이클을 가지지 않으며 m = n-1이다.
(5) G는 어느 한 연결선만 첨가하더라도 사이클을 형성하게 된다.
방향이 있고 순서화된 트리는 다음의 성질들을 만족하는 방향 그래프임
1) 선행자가 없는 '루트'라고 불리는 노드가 하나 있으나, 이 루트에서는 모든 노드로 갈수 있는 경로가 있음
2) 루트를 제외한 모든 노드들은 오직 하나씩만의 선행자(부모)를 가짐
3) 각 노드의 후속자들은 통상 왼쪽으로부터 순서화 됨
- 어떤 방향트리를 그릴 때 그 트리의 루트는 가장 위에 있음
- 아크(연결선)들은 밑을 향하여 그려짐
정의 8-3. 트리 T가 n-트리(n-ary tree)란 말은 모든 중간 노드들이 최대 n개의 자식노드를 가질 때를 말하며, 특히 n이 2인 경우를 이진트리(binary tree)라고 한다.
정의 8-4. 이진트리 (binary tree)는 노드들의 유한 집합으로서,
1) 공집합이거나
2) 루트가 왼쪽 서브트리, 오른쪽 서브트리로 이루어진다.
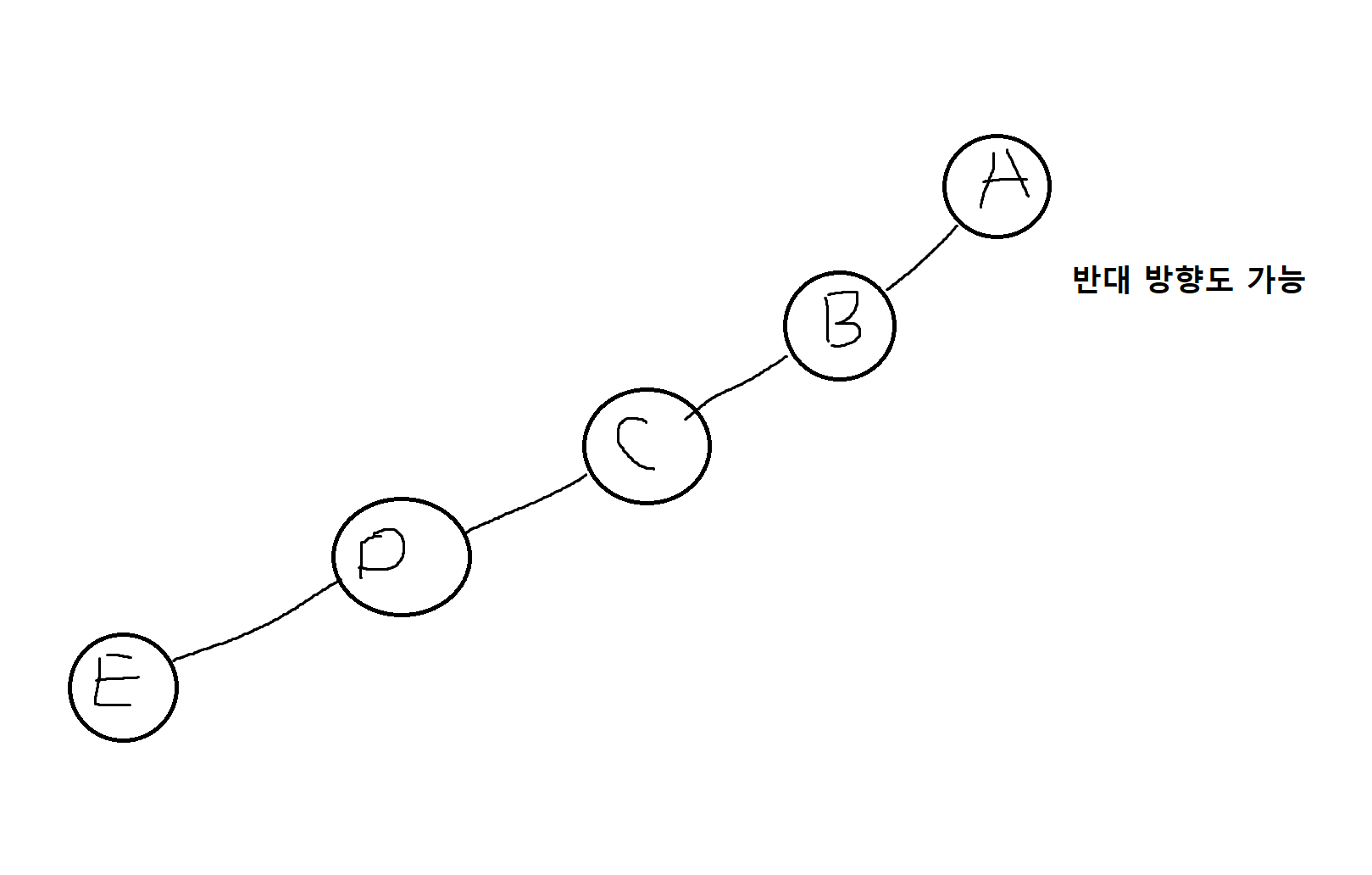
사항 이진트리 (skewed binary tree)
왼쪽 또는 오른쪽으로 편향된 트리의 구조를 가짐. (좋은 형태는 아님)
완전이진트리 (Complete binary tree)
높이가 k일 때 레벨 0부터 k-1까지는 모두 차 있고 레벨 k에서는 왼쪽 노드부터 차례로 차있는 이진트리임
포화이진트리 (full binary tree)
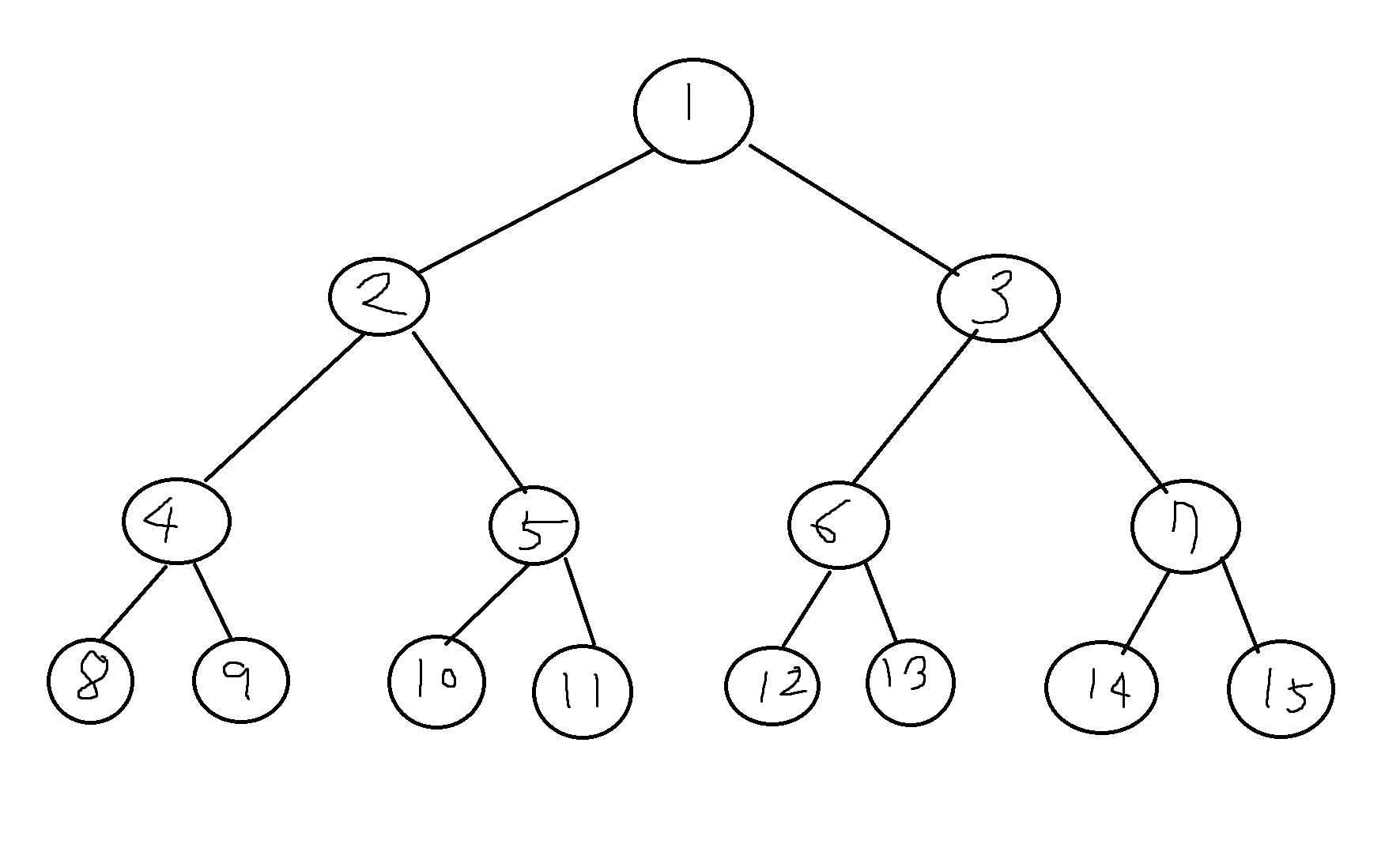
높이 k에 대해 다 찬 경우
-> 잎노드가 아닌것들은 모두 2개씩의 자식노드를 가지며 트리의 높이가 일정한 경우를 말함. 즉, 완전 이진트리에서 전체가 꽉 차있는 경우임
정리 8-3. 이진트리가 레벨 i에서 가질 수 있는 최대한의 노드수는 2^i개이며, 높이가 k인 이진트리가 가질 수 있는 최대한의 전체노드수는 (2^(k+1)) -1이다. 예를 들어, 레벨2의 경우에는 최대한 2²개의 노드를 가질 수 있고, 전체적으로는 (2^(k+1)) -1, 즉 7개를 가질 수 있다.
정의 8-4. 이진트리에서 잎노드의 개수를 n0, 차수가 2인 노드의 개수를 n₂라고 할 때, n0 = n₂+1의 식이 항상 성립한다.
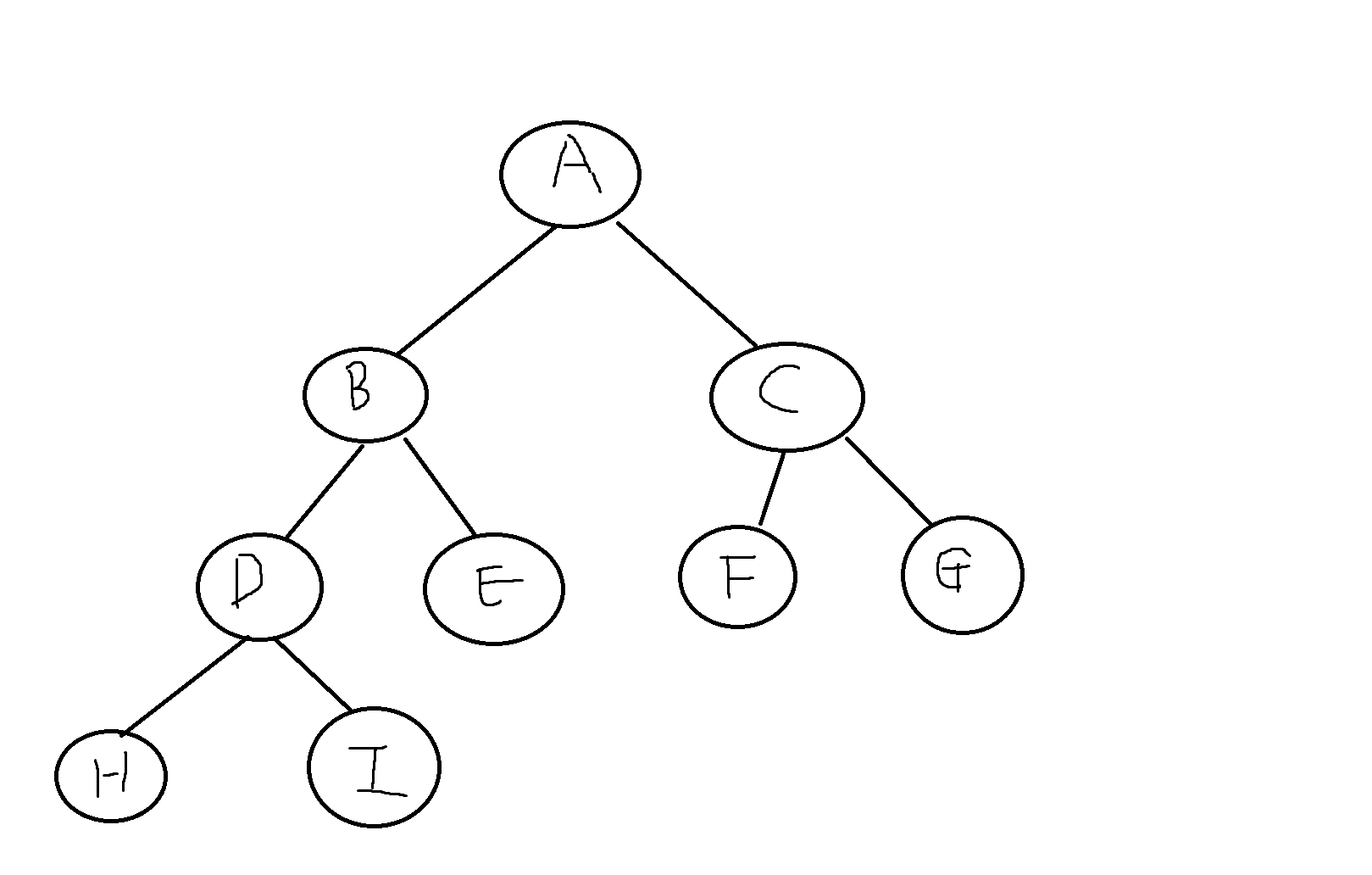
n0(잎의 개수) = 5
n₂(4)
5 = 4 + 1
요약
-
트리는 특별히 지정된 노드인 루트가 있고, 나머지 노드들은 자신의 트리인 서로 겹치지 않는 T₁,T₂...Tn과 같은 서브트리로 이루어진다.
-
트리에서 사용되는 용어들은 루트, 차수, 잎노드, 자식노드, 부모노드, 형제노드, 중간노드, 레벨, 조상, 자손, 숲 등이다.
-
트리는 연결되어 있고 사이클이 없는 그래프로서 어느 한 연결선만 첨가하더라도 사이클을 형성하게 된다.
-
트리 T가 n-트리란 말은 모든 중간노드들이 최대 n개의 자식노드를 가질 때를 말하며, 특히 n이 2인 경우를 이진트리라고 한다. 이진트리는 루트와 왼쪽 서브트리 그리고 오른쪽 서브트리로 이루어진다.
-
이진 트리에는 사향이진트리, 완전이진트리, 포화이진트리 등이 있으며, 이진트리가 레벨 i에서 가질 수 있는 최대한의 노드 수는 2^i개이고, 높이가 k인 이진트리가 가질 수 있는 최대한의 전체 노드수는 (2^(k+1))-1 이다.
연습문제
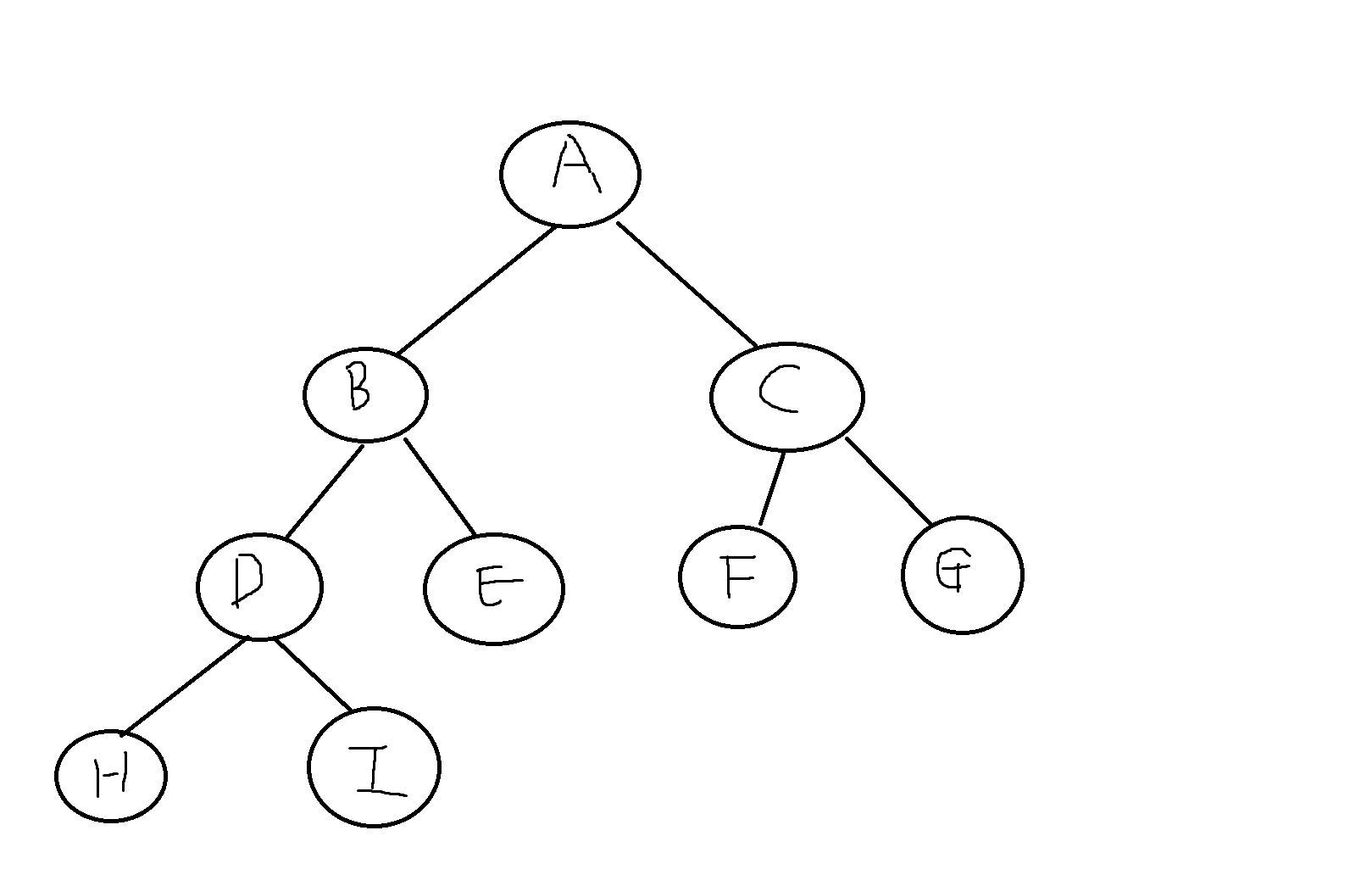
1) 다음 주어진 이진트리에서 다음에 해당하는 노드들을 모두 답하시오
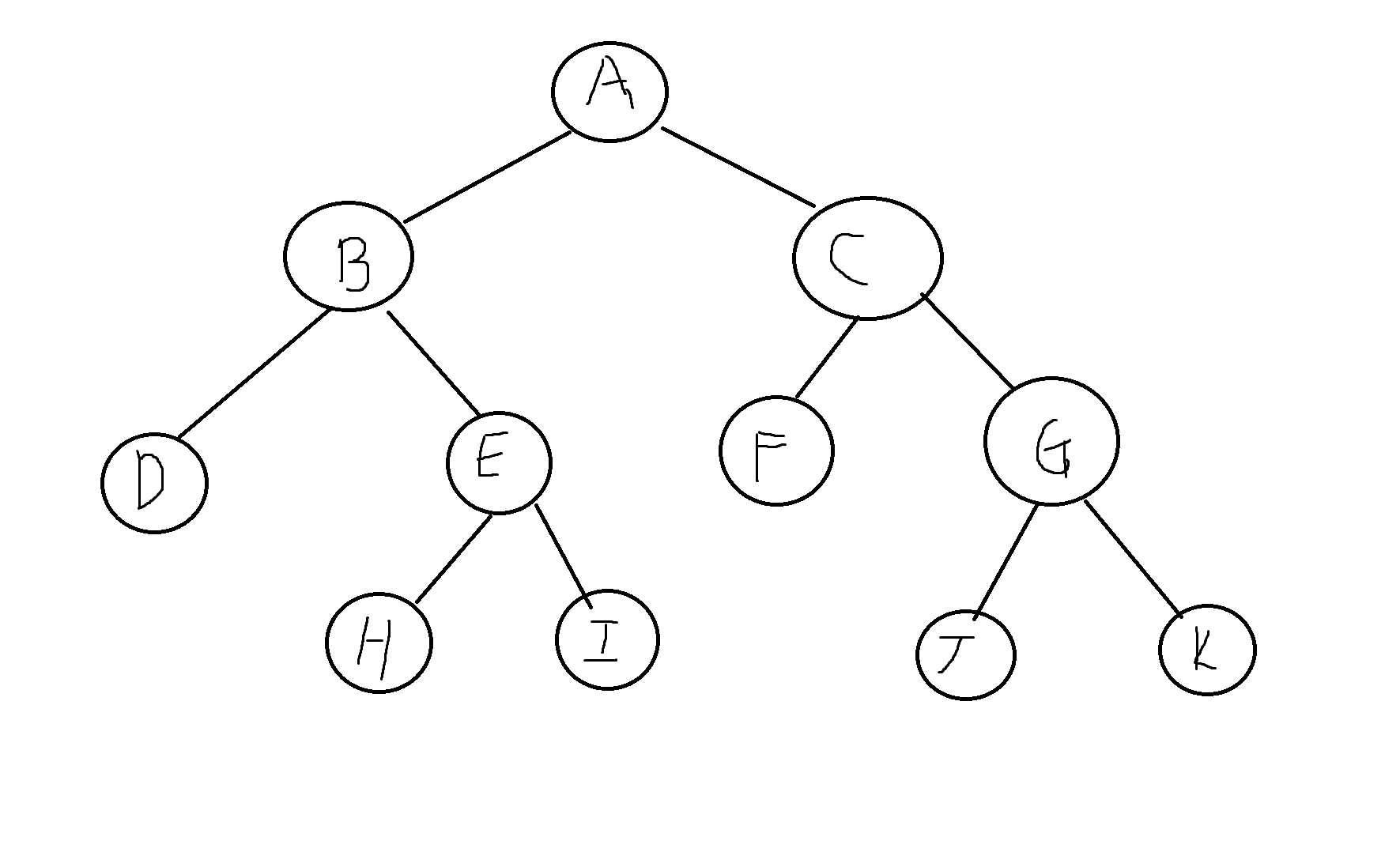
1) 잎노드 -> D,H,I,J,K
2) 루트노드 -> A
3) C의 부모노드 -> A
4) E의 조상노드 -> B, A
5) E의 후손노드 -> H, I
6) D의 형제노드 -> E
7) C의 레벨 -> 1
8) A의 높이 -> 3
2) 이진 트리에서 루트 노드의 높이를 0이라고 가정할 때, 높이가 50인 이진트리가 가질 수 있는 노드의 최소 개수와 최대 개수는 각각 몇개인가?
최소 -> 50+1 = 51개 (루트 1개 포함)
최대 -> 2^51 -1 개
이진트리를 표현하는 방법
- 배열(array)에 의한 방법과 연결리스트(linked list)에 의한 방법으로 나눌 수 있다
- 배열에 의한 방법은 구현하기는 쉽지만 트리의 중간에 새로운 노드를 삽입하거나 기존의 노드를 지울경우 비효율적임
| Arr[0] | [1] | [2] | [3] | [4] | [5] | [6] | [7] |
|---|---|---|---|---|---|---|---|
| C | O | M | P | U | T | E | R |
만약 Arr[5]에 x를 삽입하려면 -> 3번 이동이 필요함
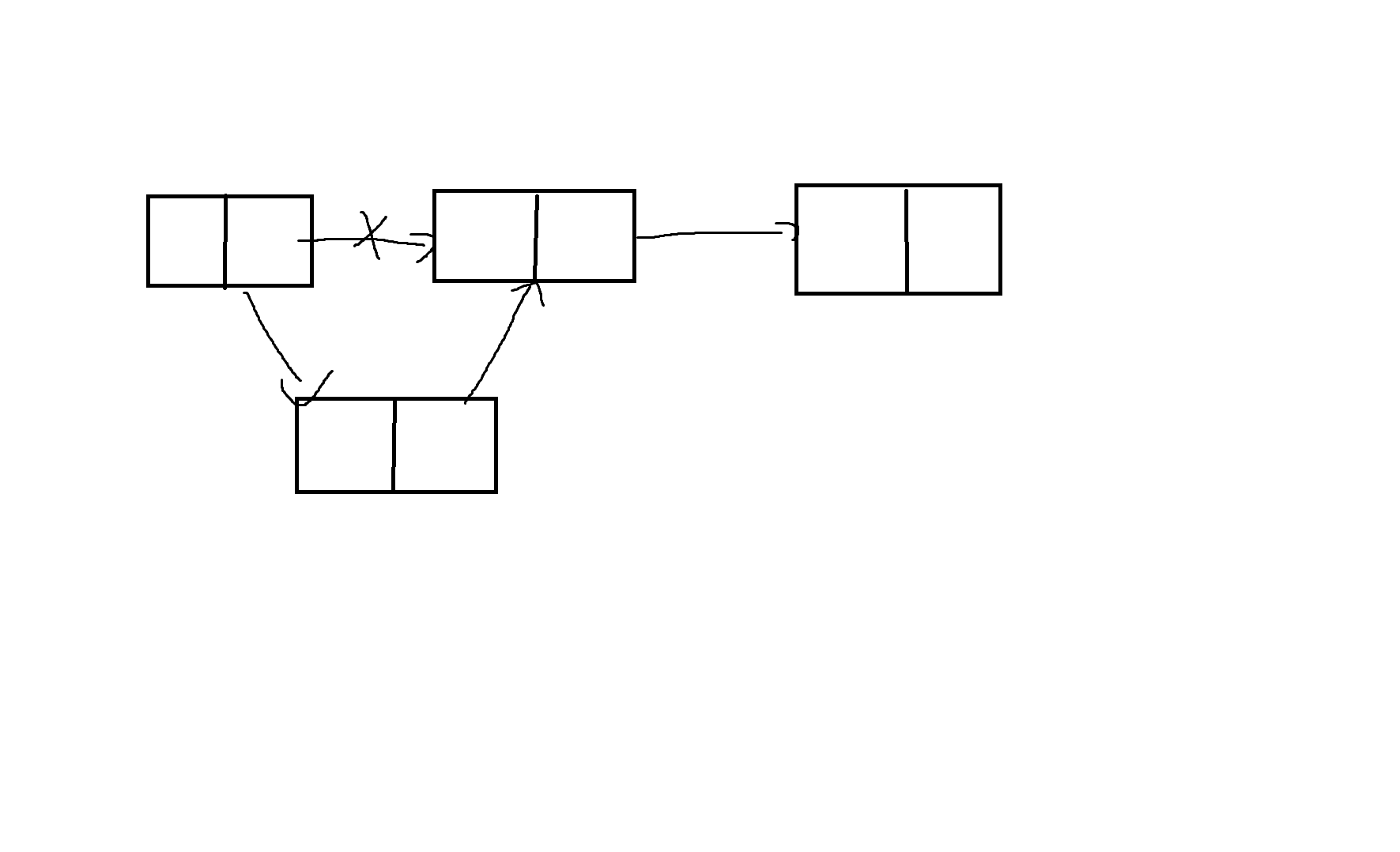
연결리스트의 경우 값의 삽입이 간단하다
이진트리를 표현하는 방법
- 일반적으로 가장 많이 쓰이는 방법은 연결리스트에 의한 방법임. 데이터(data)를 저장하는 중간부분, 왼쪽 자식(left child), 오른쪽 자식(right child)을 각각 가리키는 포인터(Pointer) 부분으로 구성되며, C언어로 나타낼 수 있음
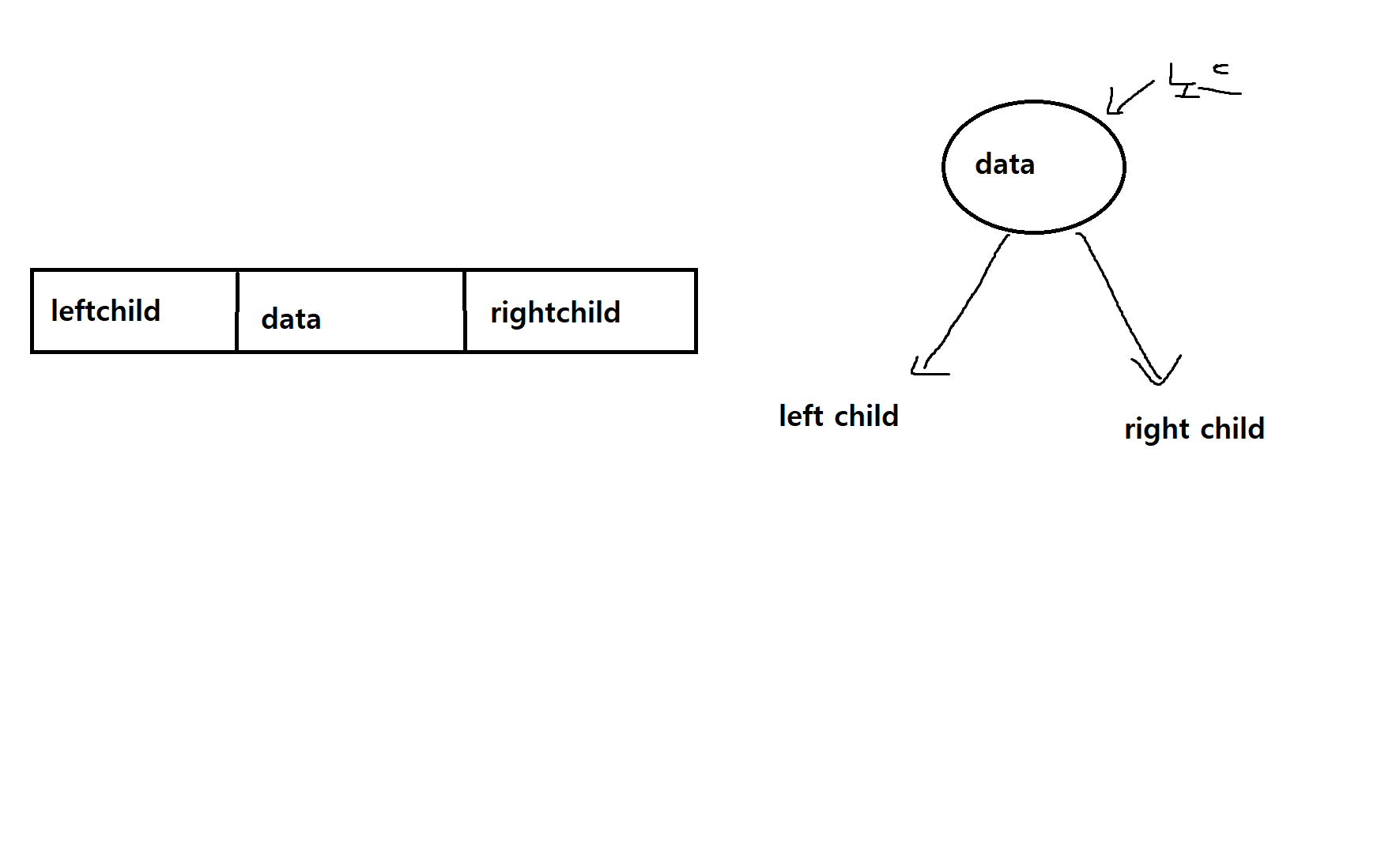
typedef struct treenode
{
struct treenode *leftchild;
char data;
struct treenod *rightchild;
}이진트리의 연결리스트에 의한 표현
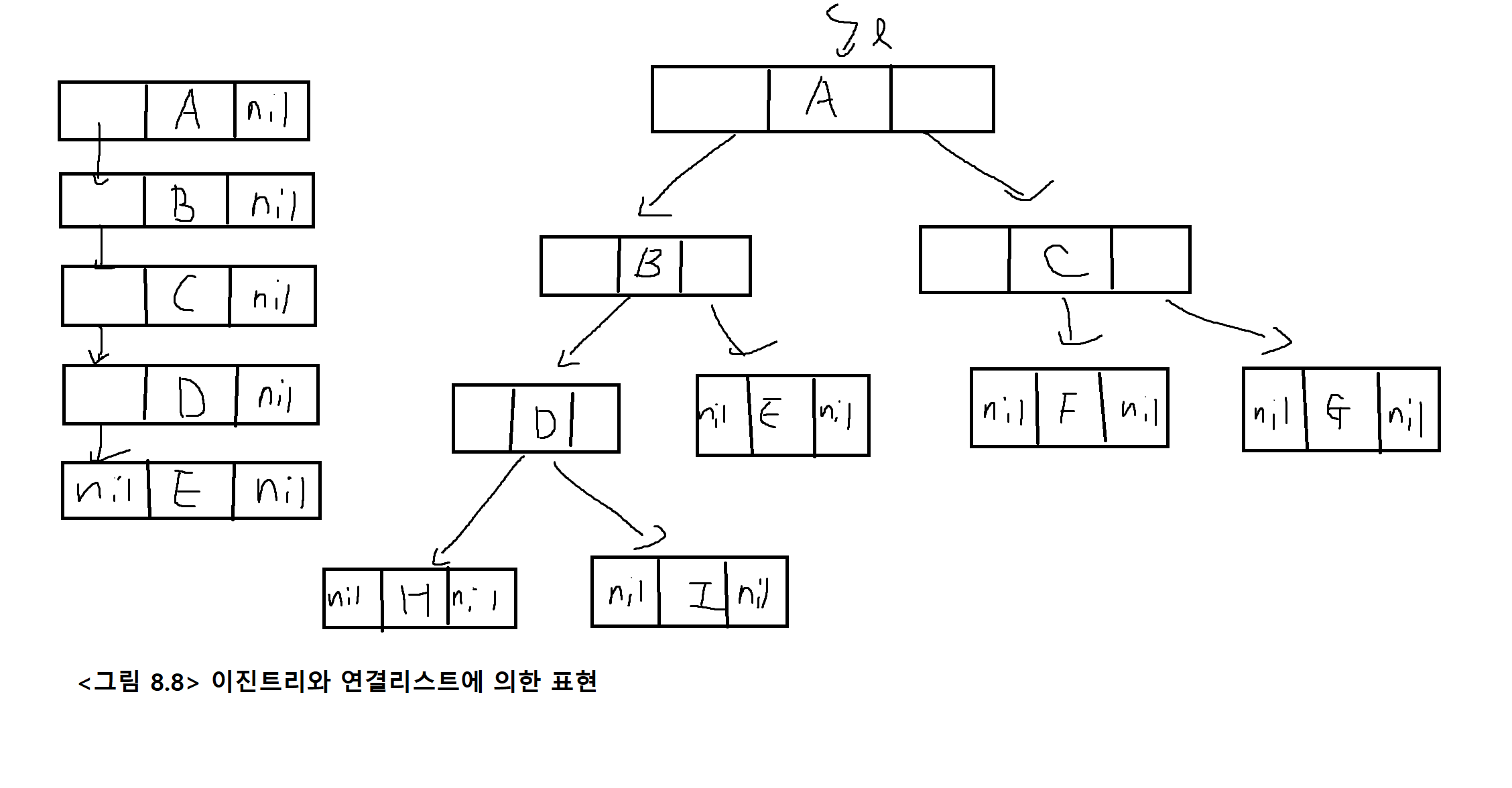
-
트리는 자료의 저장과 검색에 있어서 매우 중요한 구조를 제공함.
-
트리에서의 연산에는 여러가지가 있으나 가장 빈번하게 하는 것은 각 노드를 꼭 한번씩만 방문하는 탐방 (traversal)일 것임
-
탐방의 결과 각 노드에 들어있는 데이터를 차례로 나열하게 됨
-
이진트리를 탐방하는 것은 여러가지 응용에 널리 쓰임
-
각 노드와 그것이 서브트리를 같은 방법으로 탐방할 수 있음
트리탐방의 세 가지 방법은 다음과 같다.
(1) 중순위 탐방
(2) 전순위 탐방
(3) 후순위 탐방
-
L,D,R을 각각 왼쪽(left), 데이터(Data)프린트, 오른쪽(Right)으로의 이동을 나타낸다고 할때 총 6가지의 나열방법이 있음
(LDR, LRD, DLR, DRL, RLD, RDL) -
왼쪽을 오른쪽보다 항상 먼저 한다고 가정하면 LDR, DLR, LRD의 3가지 경우가 있음
-
이것을 각각 중순위(inorder), 전순위(preorder), 후순위(postorder) 탐방이라고 한다. (데이터를 중심으로)
-
이 순서들을 수식표현에서 중순위 표기 (infix), 전순위 표기 (prefix), 후순위 표기 (postfix)와 각각 대응함
정의 8-5. 중순위 탐방 (inorder traversal)은 루트에서 시작하여 트리의 각 노드에 대하여 다음과 같은 재귀적 (recursive) 방법으로 정의된다.
(1) 트리의 왼쪽 서브트리를 탐방한다.
(2) 노드를 방문하고 트리를 프린트한다.
(3) 트리의 오른쪽 서브트리를 탐방한다.
void inorder(TREE *currentnode)
{
if (currentnode != Null)
{
inorder(currentnode -> leftchild);
printf("%c", currentnode -> data);
inorder(currentnode -> rightchild);
}
}중순위 탐방의 재귀적 알고리즘 (Recursive Algorithm)
중순위 담방은 루트로부터 시작하여
inorder(currentnode -> leftchild)
printf(currentnode -> data)
inorder(currentnode -> rightchild)
의 트리형태로 계속 전개시켜 나가서 프린트 된 결과를 왼쪽부터 차례로 적어나감 (가장 쉽고도 정확한 방법)
정의 8-6. 전순위 탐방 (Preorder traversal)은 루트에서 시작하여 트리의 각 노드에 대하여 다음과 같은 재귀적 방법으로 정의된다.
(1) 노드를 탐방하고 데이터를 프린터한다.
(2) 트리의 왼쪽 서브트리를 탐방한다.
(3) 트리의 오른쪽 서브트리를 탐방한다.
void preorder(TREE *currentnode)
{
if (currentnode != Null)
{
printf("%c", currentnode -> data);
preorder(currentnode -> leftchild);
preorder(currentnode -> rightchild);
}
}전순위 탐방 (D, L, R)
printf(currentnode -> data)
preorder(currentnode -> leftchild)
preorder(currentnode -> rightchild)
정의 8-7. 후순위 탐방 (Postorder traversal)은 루트에서 시작하여 트리의 각 노드에 대하여 다음과 같은 재귀적 방법으로 정의된다.
(1) 트리의 왼쪽 서브트리를 탐방한다.
(2) 트리의 오른쪽 서브트리를 탐방한다.
(3) 노드를 탐방하고 데이터를 프린트한다.
void postorder(TREE *currentnode)
{
if (currentnode != NULL)
{
postorder(currentnode -> leftchild);
postorder(currentnode -> rightchild);
printf("%c", currentnode -> data);
}
}후순위 탐방 (L, R, D)
postorder(currentnode -> leftchild)
postorder(currentnode -> rightchild)
printf(currentnode -> data)
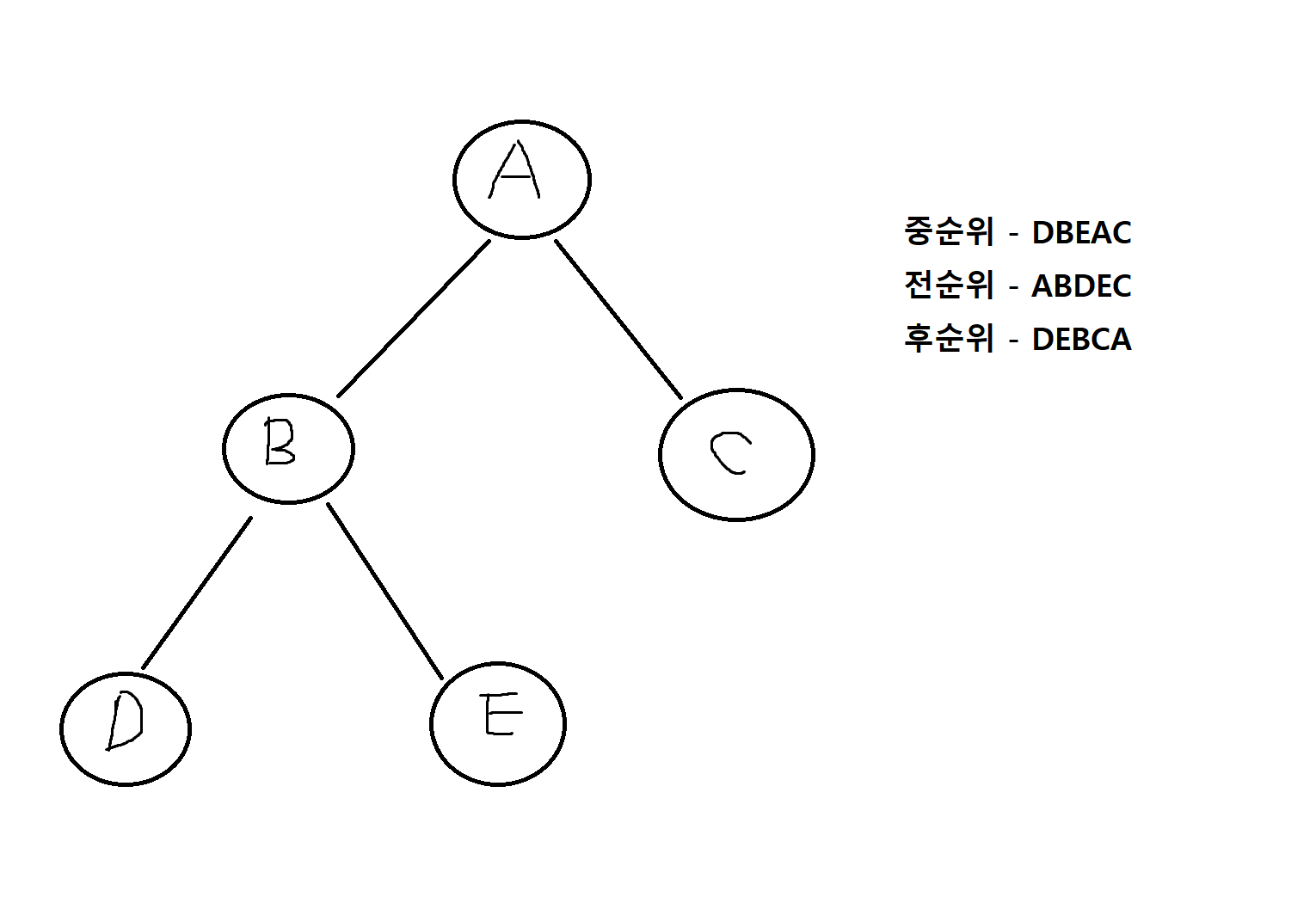
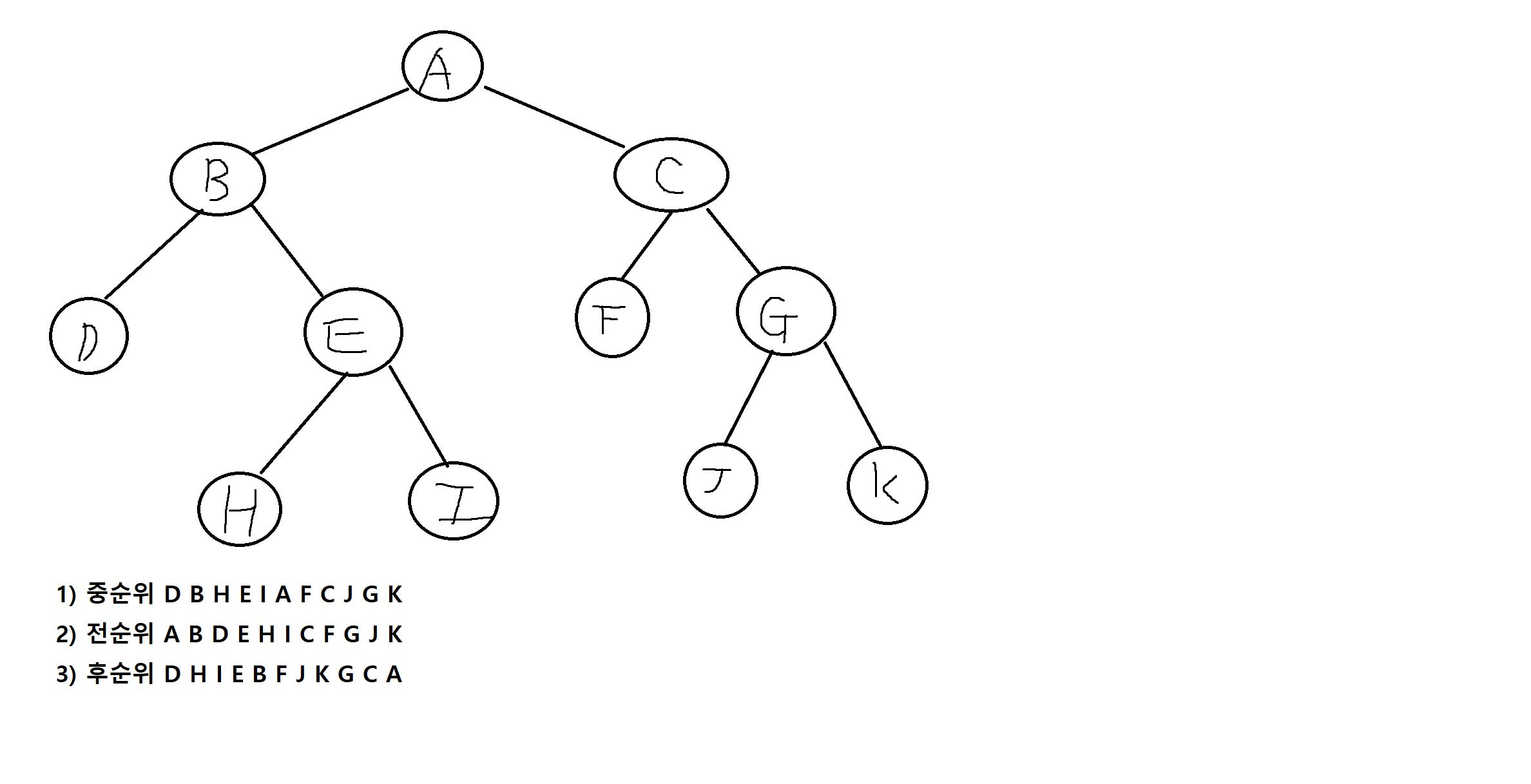
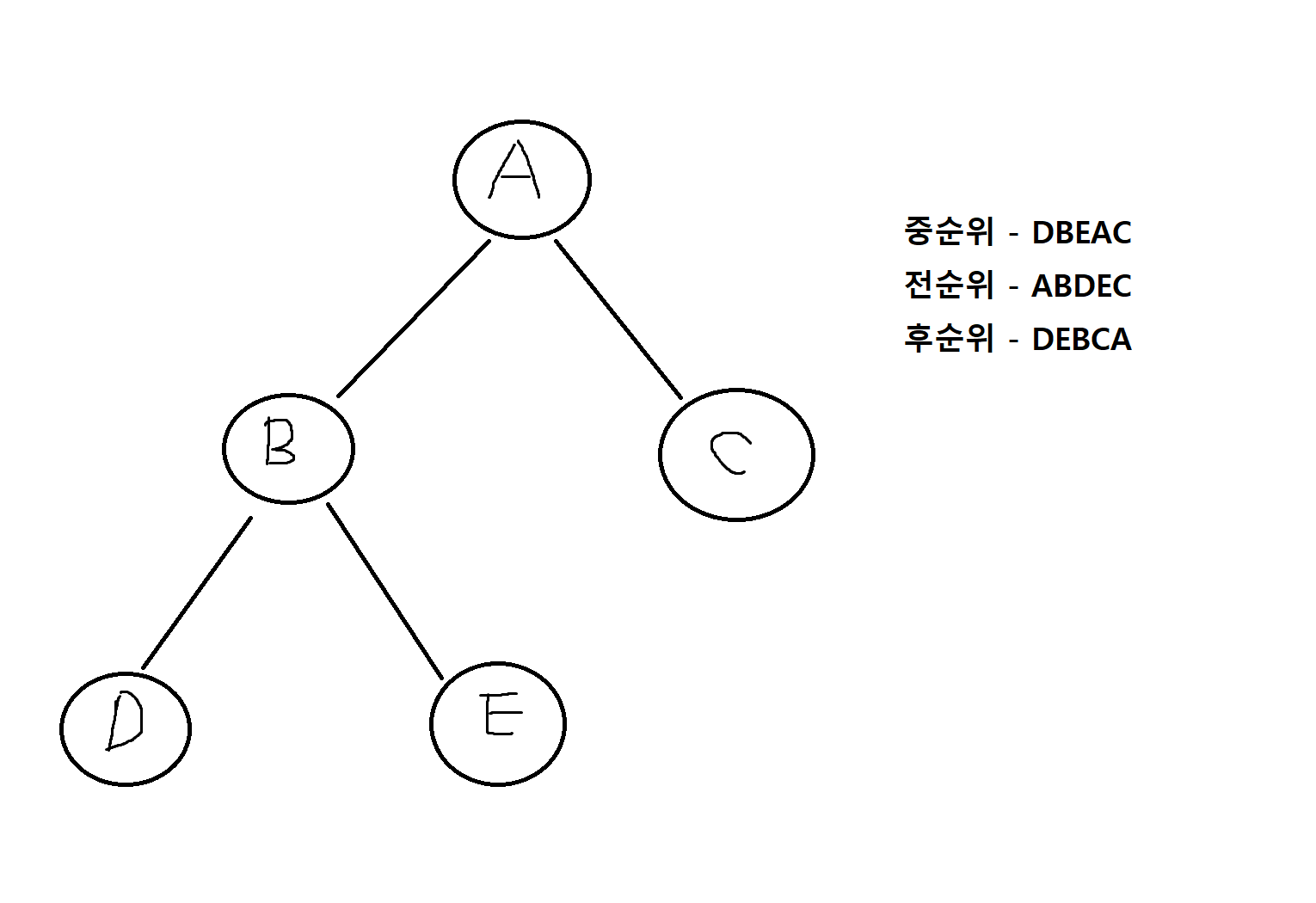
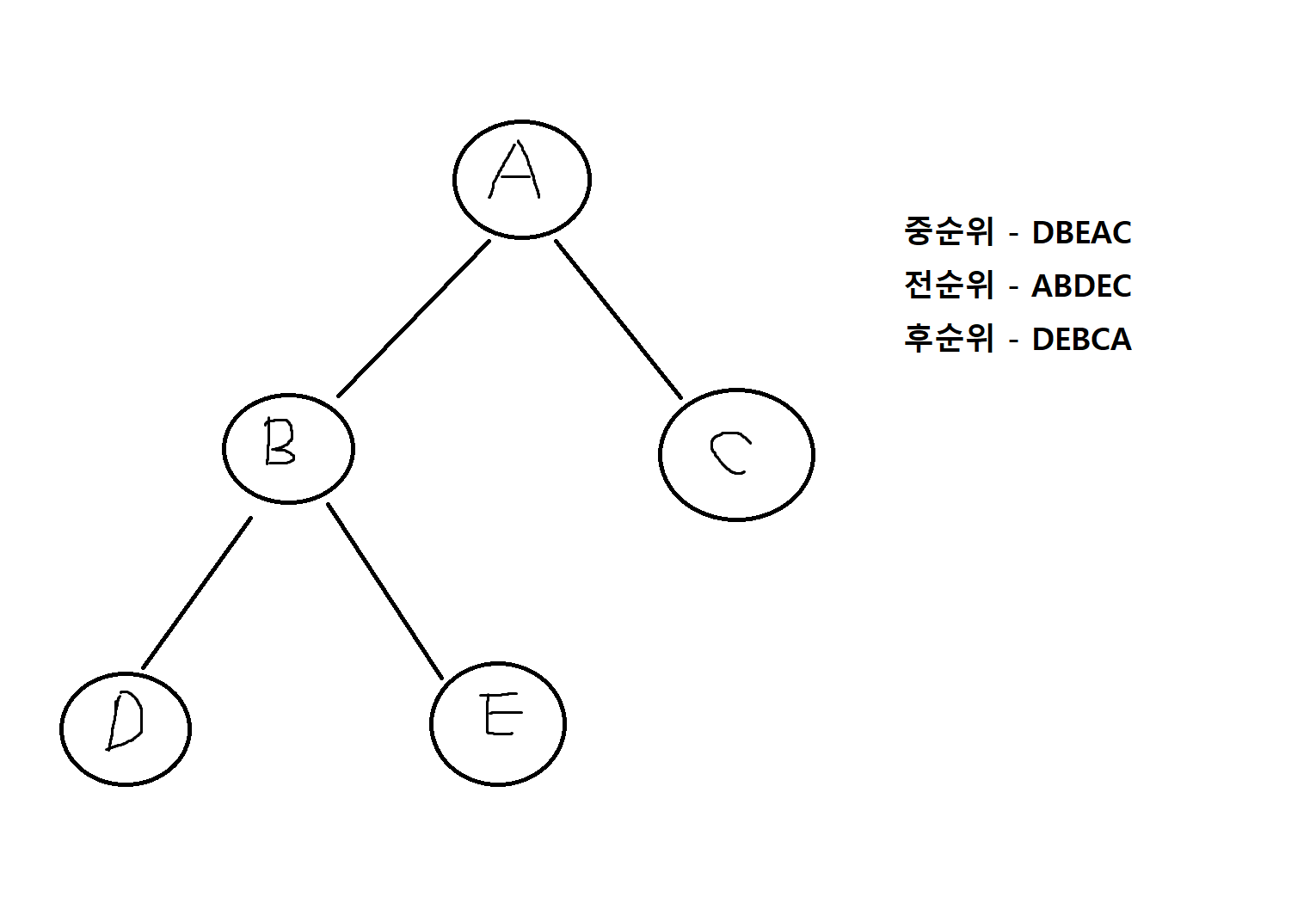
예제 8-4. 다음의 이진트리에서 중순위 탐방, 전순위 탐방, 후순위 탐방의 결과를 각각 구해보자.
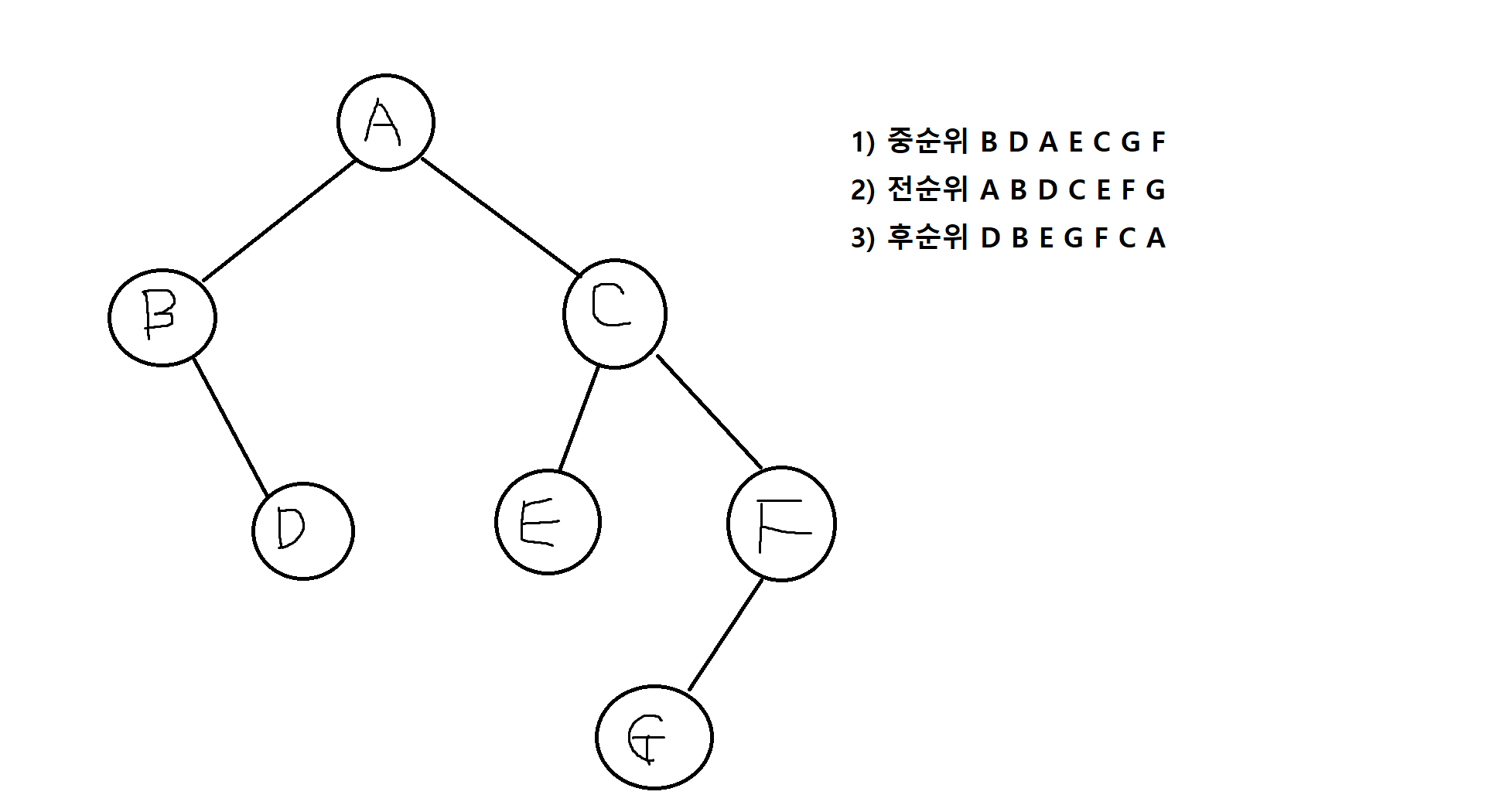
연습문제
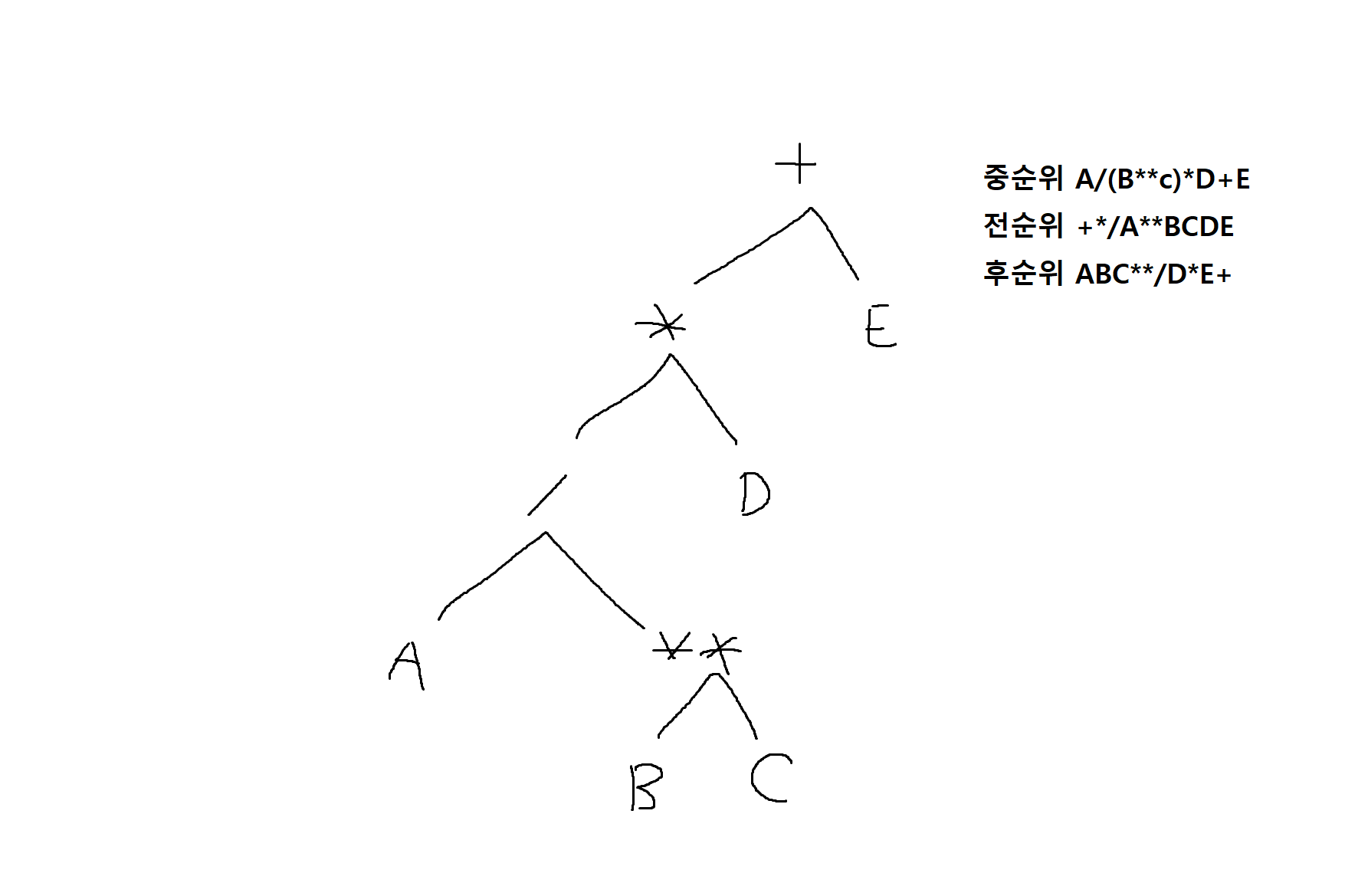
1) 다음 수식을 이진트리로 나타내고, 중순위, 전순위, 후순위 탐방의 결과를 각각 밝히시오
A / (B ** C) * D + E
2) 다음의 트리에서 중순위, 전순위, 후순위 탐방의 결과를 각각 밝히시오