이산수학(17) - 트리(2)

생성트리와 최소비용 생성트리

정의 8-8. 어떤 그래프 G에서 모든 노드들을 포함하는 트리를 생성트리(Spanning tree)라고 한다.

G = (V,E)

주어진 그래프 G와 그것의 3가지 생성트리들

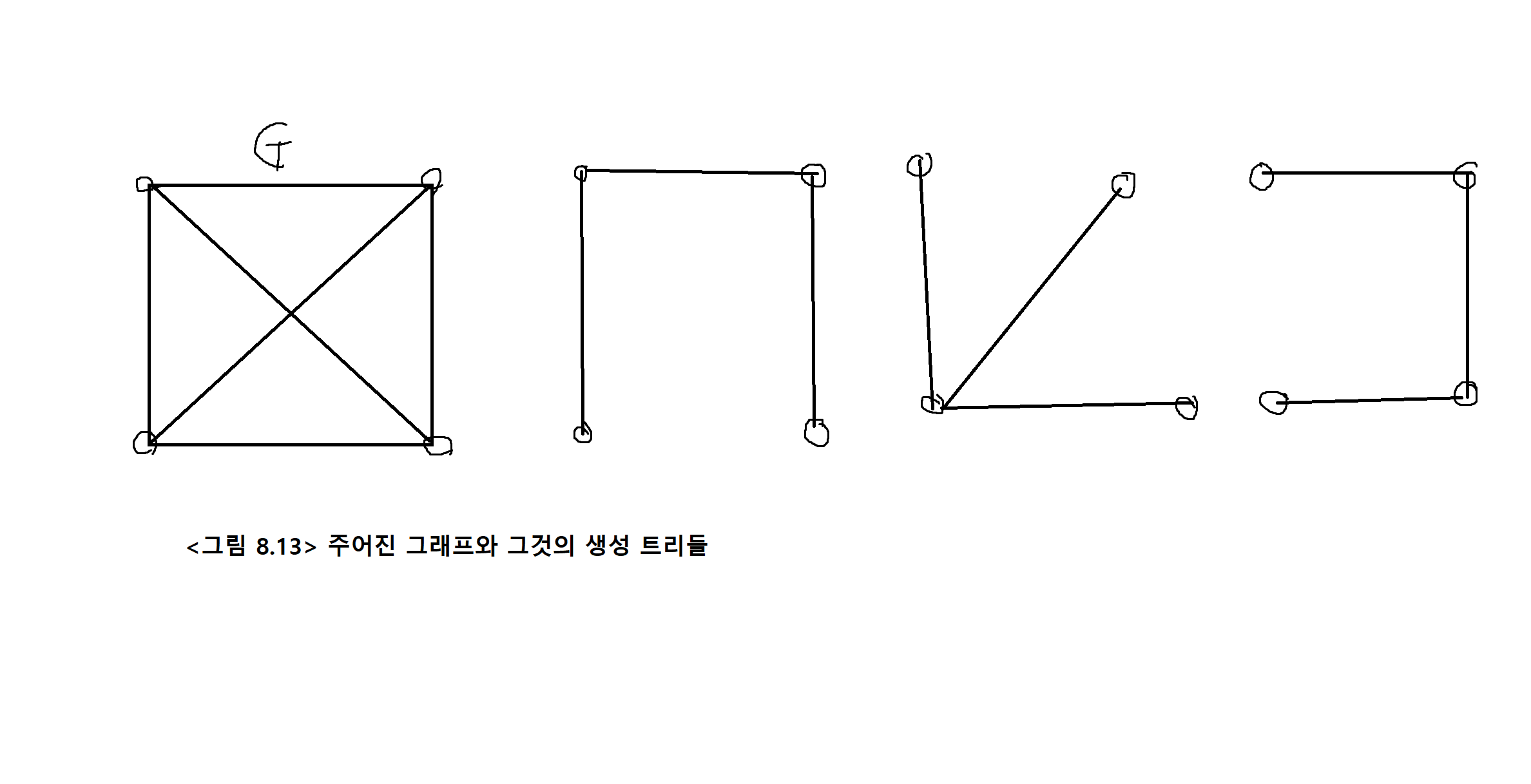
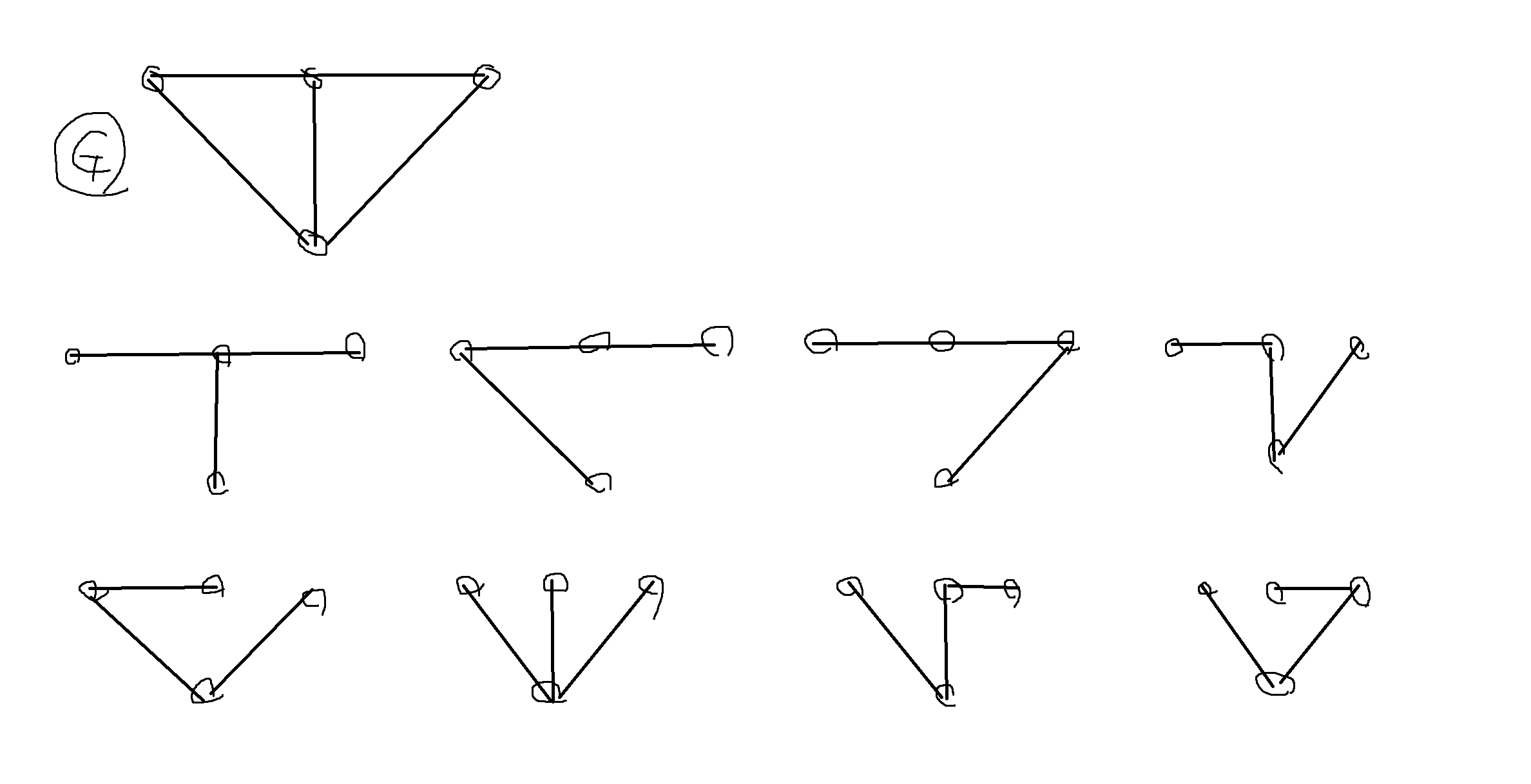
예제 8-5. 다음과 같은 그래프 G의 생성트리를 모두 구해보자.

생성트리 (G의 정점을 모두 가지고 edge로만 구성됨)

정의 8-9. 생성트리의 비용(cost)은 트리 연결선의 값을 모두 합한 값이다.

정의 8-10. 최소비용 생성트리 (Minimum Spanning Tree : MST)란 최소한의 비용을 가지는 생성트리를 말한다.

• 최소비용 생성트리의 대표적인 예는 통신 네트워크의 연결임
• 각 도시들을 연결하는데 있어서 최소 비용으로 연결하는 방법을 찾는 것임
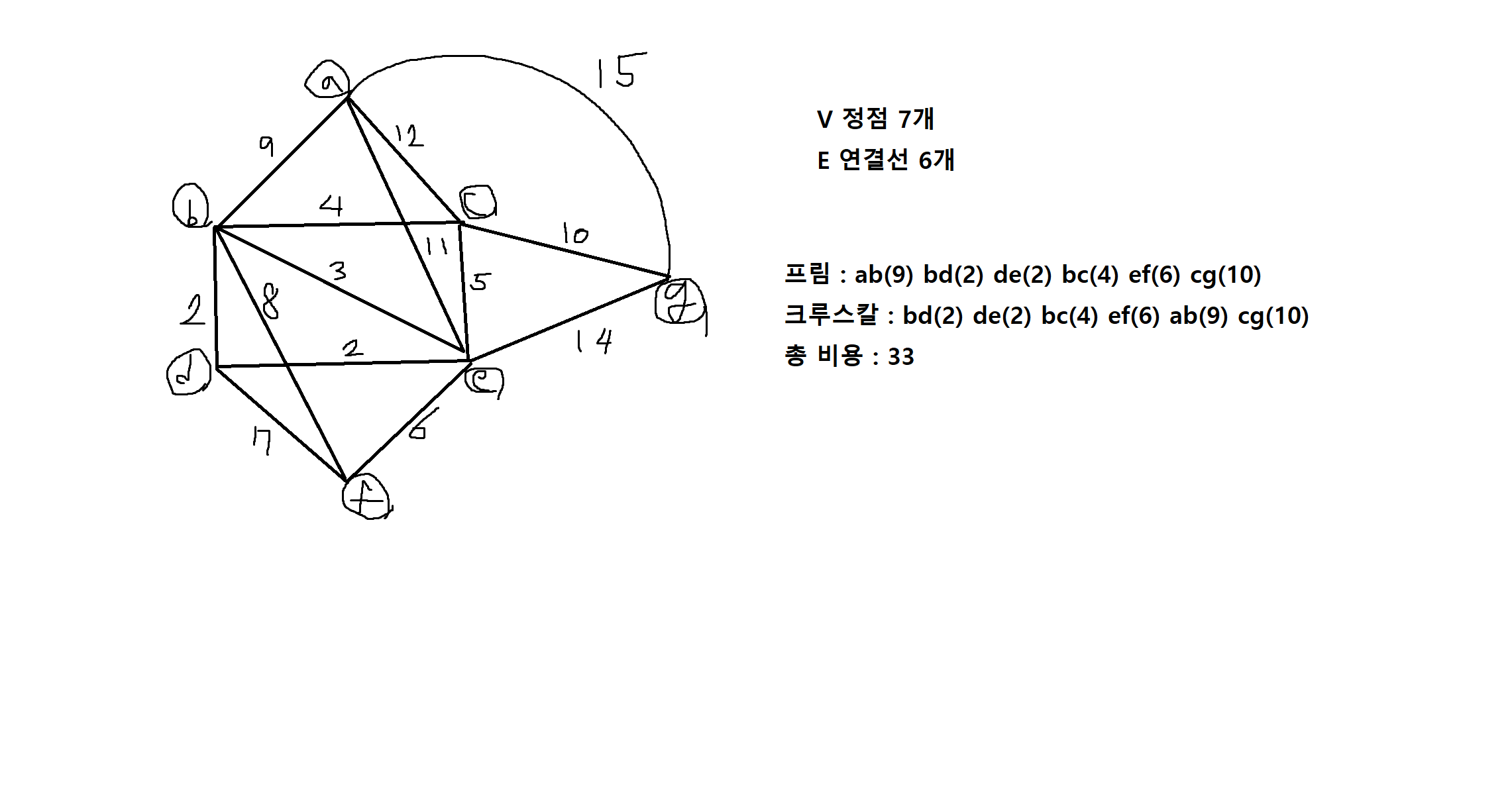
• 최소비용 생성트리의 대표적인 2가지 방법은 프림(Prim)의 알고리즘과 크루스칼(kruskal)의 알고리즘임

프림의 알고리즘

주어진 가중그래프 G = (V, E)에서 V = {1,2,...,n}이라고 하자
(1) 노드의 집합 U를 1로 시작한다.

(2) u∈U, v∈V 일 때 U와 V-U를 연결하는 가장 짧은 연결선인 (u,v)를 찾아서 v를 U에 포함시킨다. 이때 (u,v)는 사이클(cycle)을 형성하지 않는 것이어야 한다.

(3) (2)의 과정을 U = V 때까지 반복한다.

(더 간단한 설명)
1. 임의의 접점을 선택, T에 포함 (이제 T는 노드가 아닌 하나의 개인트리)
2. T에 있는 노드와 T에 없는 노드 사이의 간선 중 가중치가 최소인 간선을 찾음
3. 찾은 간선이 연결하는 두 노드 중, T에 없던 노드를 T에 포함 (2에서 찾은 간선도 같이 T에 포함)
4. 모든 모드가 T에 포함될 때 까지 2, 3 반복

void Prim(graph G: set_of_edges T)
/* 프림의 알고리즘은 G에 대한 최소 비용 생성트리를 만든다. */
{
	set_of_vertices = 0;
    vertex u, v;
    T = Null;
    U = {1};
    while(U!=V)
    {
    	let (u,v) be a lowest cost edge such that u is in U and v is in V-U;
        T = T ∪ {(u, v)};
        U = U ∪ {v};
    }
}
/*Prim*/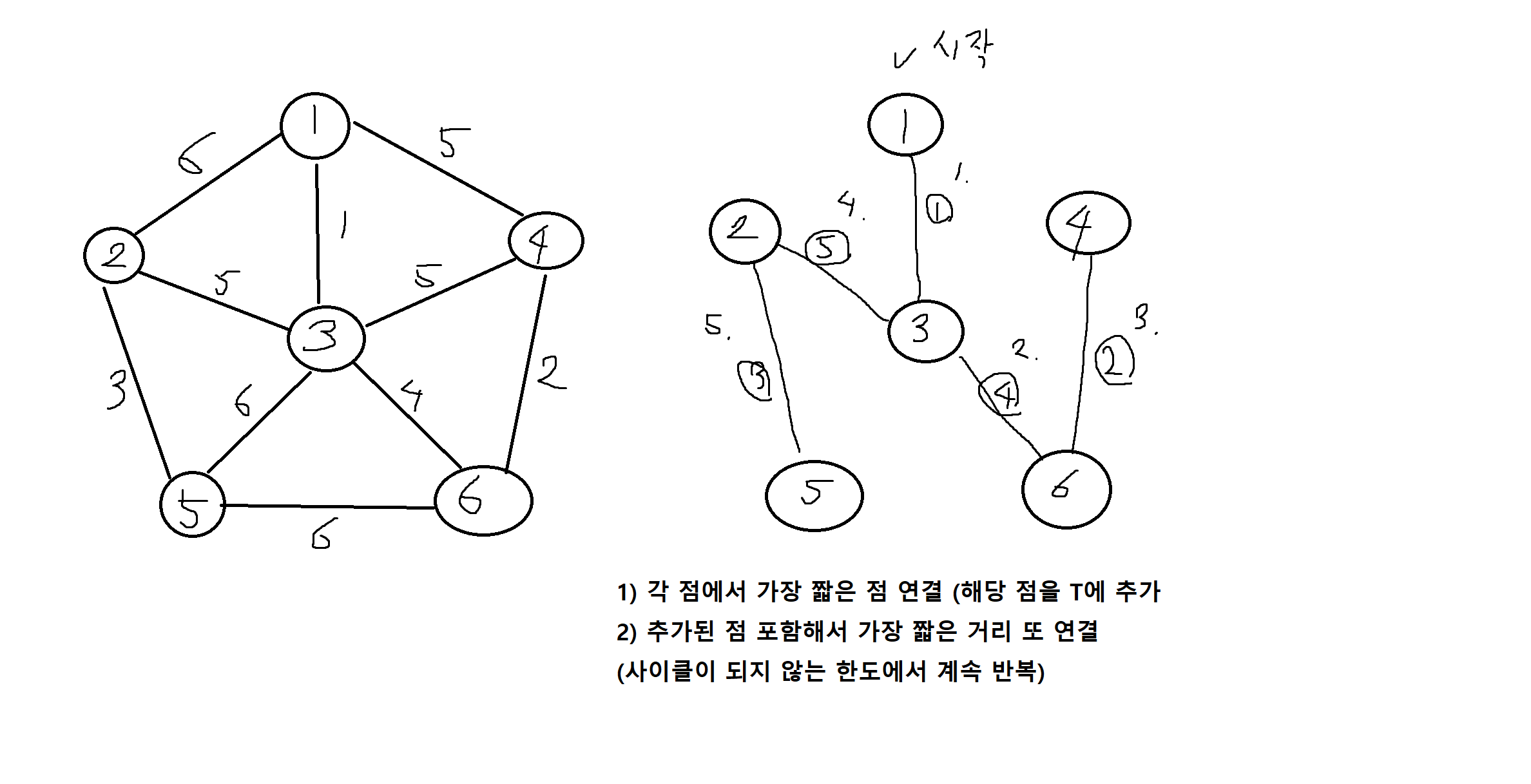

알고리즘 2 | 크루스칼의 알고리즘

주어진 가중그래프 G = (V, E)에서 V = {1,2,...n}이라고 하고 T의 연결선의 집합이라고 하자.

(1) T를 ∅으로 놓는다.
(2) 연결선의 집합 E를 비용이 적은 순서로 정렬한다.
(3) 가장 최소값을 가진 연결선 (u,v)를 차례로 찾아서 (u,v)가 사이클을 이루지 않으면 (u,v)를 T에 포함시킨다.
(4) (3)의 과정을 |T| = |V| - 1 (연결선수 = 노드수 -1)일 때까지 반복한다.

(더 간단한 설명)
1. 간선을 다 끊고 가중치를 오름차순 기준으로 정렬 (작은 것부터 확인)
2. 사이클이 아니면 연결
3. 1,2를 반복하고 모든 정점이 연결되면 종료

/* 크루스칼 */

T = Null;
while (T contains less than n-1 edges and E not empty)
{
	choose an edge (v,w) from E of lowest cost;
    delete (v,w) from E;
    if ((v,w) does not create a cycle in T)
    	add (v,w) to T;
    else discard (v,w);
}
if (T constrains fewer than n-1 deges)
	printf("no spanning tree"\n);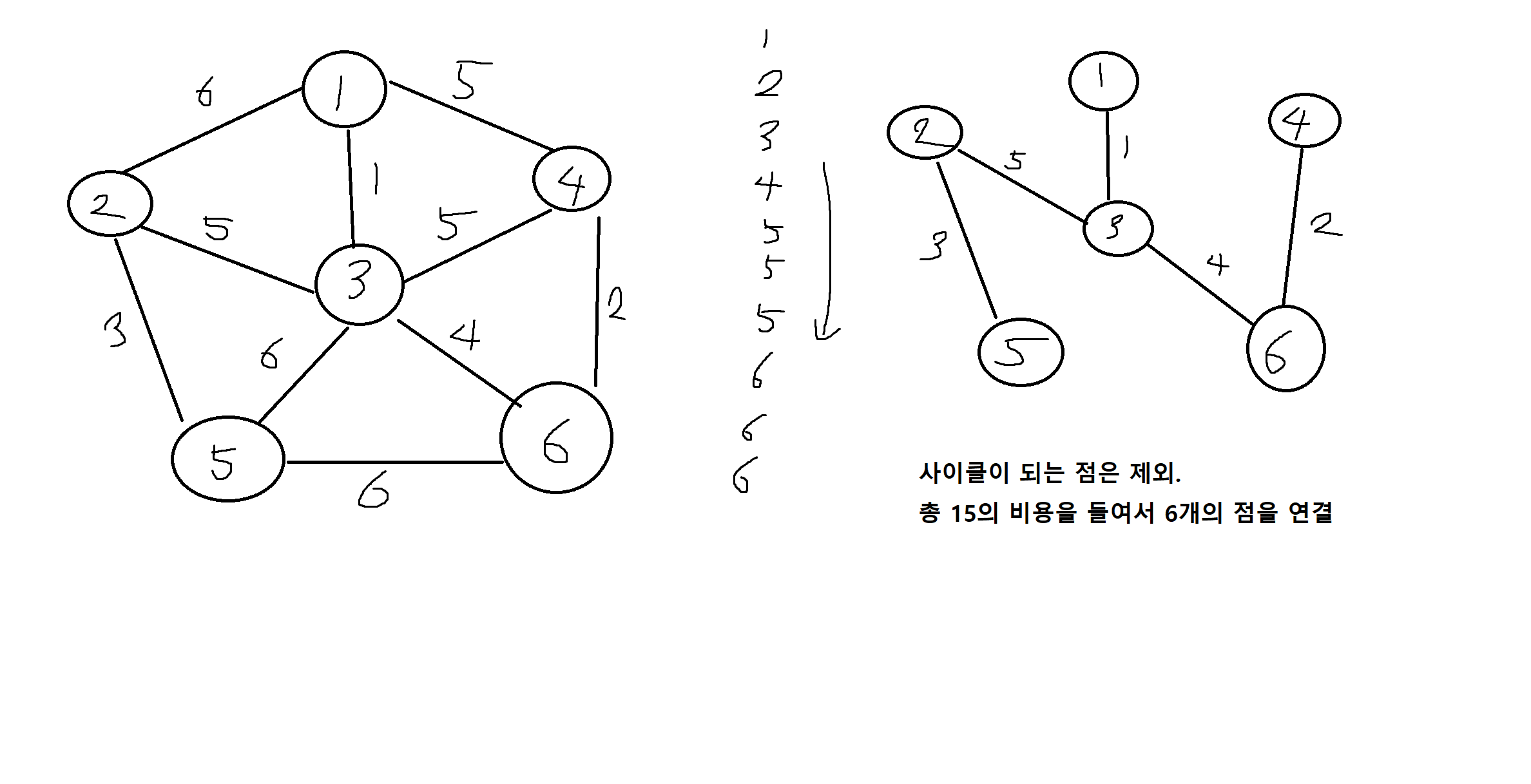

요약

• 어떤 그래프 G에서 모든 노드들을 포함하는 트리를 생성트리라고 하며, 생성트리의 비용은 트리 연결선의 값을 합한 값이다.

• 최소비용 생성트리란 최소한의 비용을 가지는 생성트리를 말하는데, 최소비용 생성트리를 구하는 2가지 방법은 프림 알고리즘과 크루스칼 알고리즘이다.

연습문제

1) 다음 그래프에서 최소비용 생성트리를 a로 시작하는 경우 프림의 알고리즘과 크루스칼의 알고리즘을 이용하여 각각 구하고 생성트리의 비용을 나타내시오.

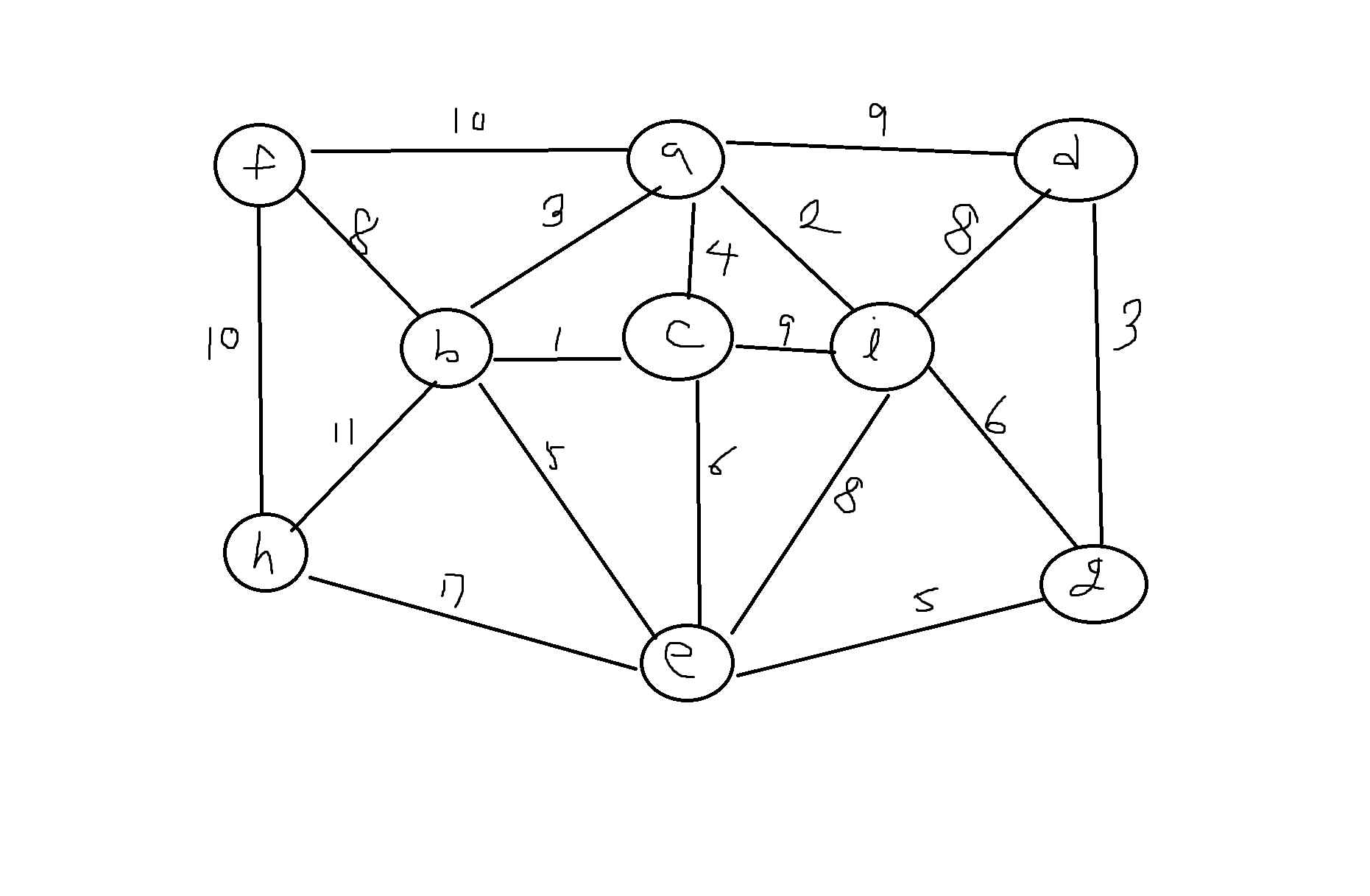
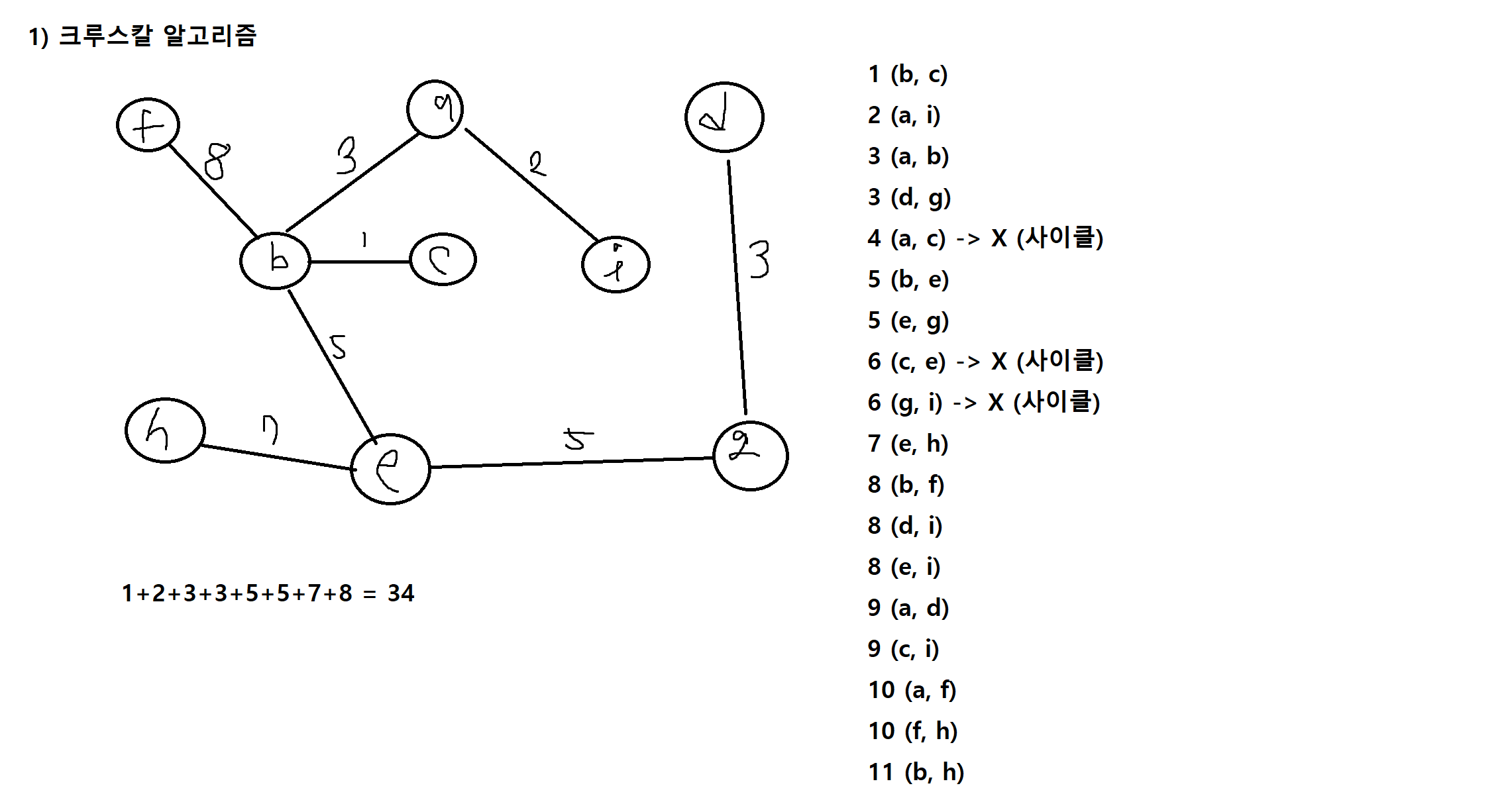
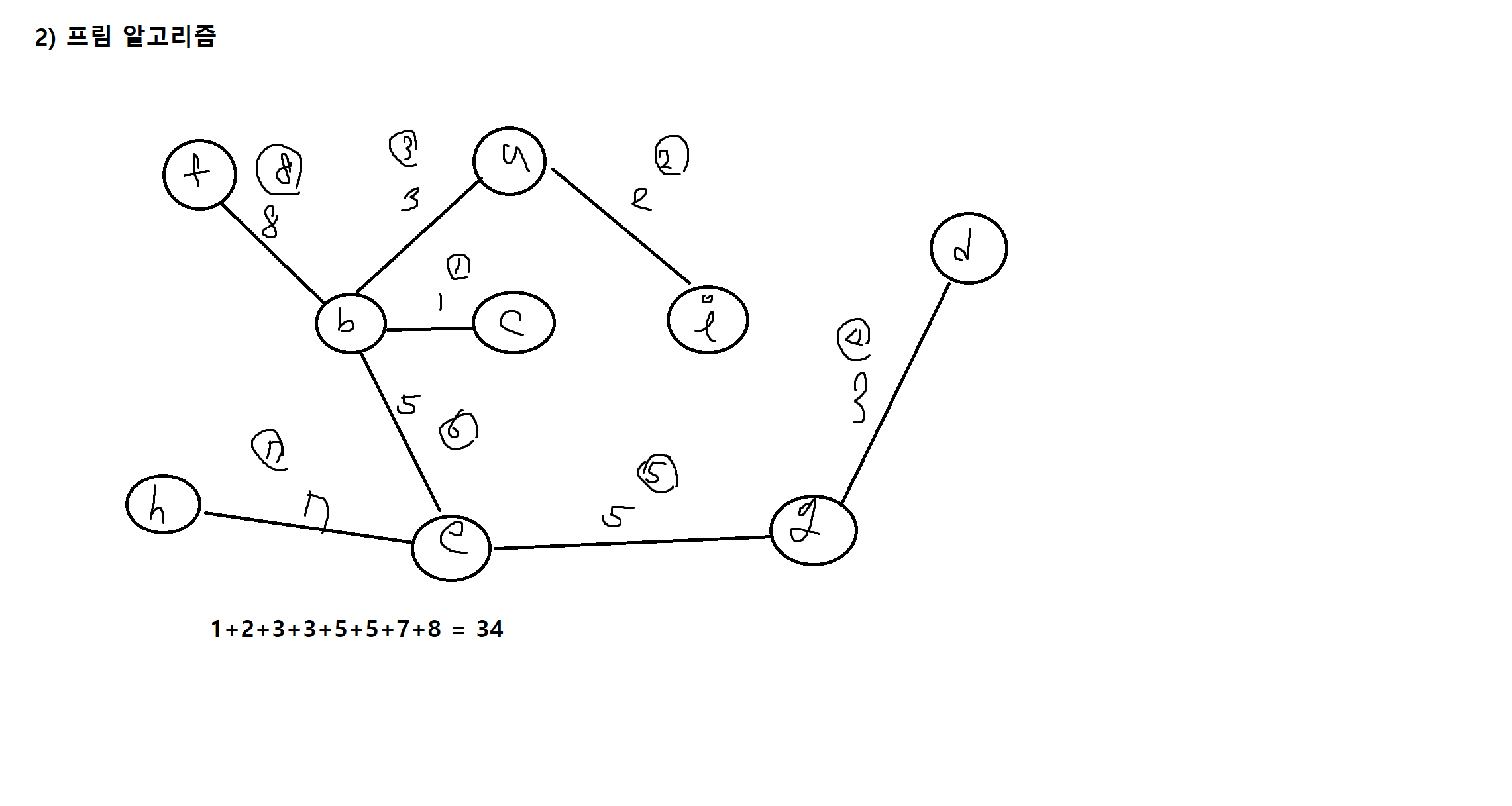
2) 다음 그래프에서 최소비용 생성트리를 a로 시작하는 경우 프림의 알고리즘과 크루스칼의 알고리즘을 이용하여 각각 구하고, 생성 트리의 비용을 나타내시오.

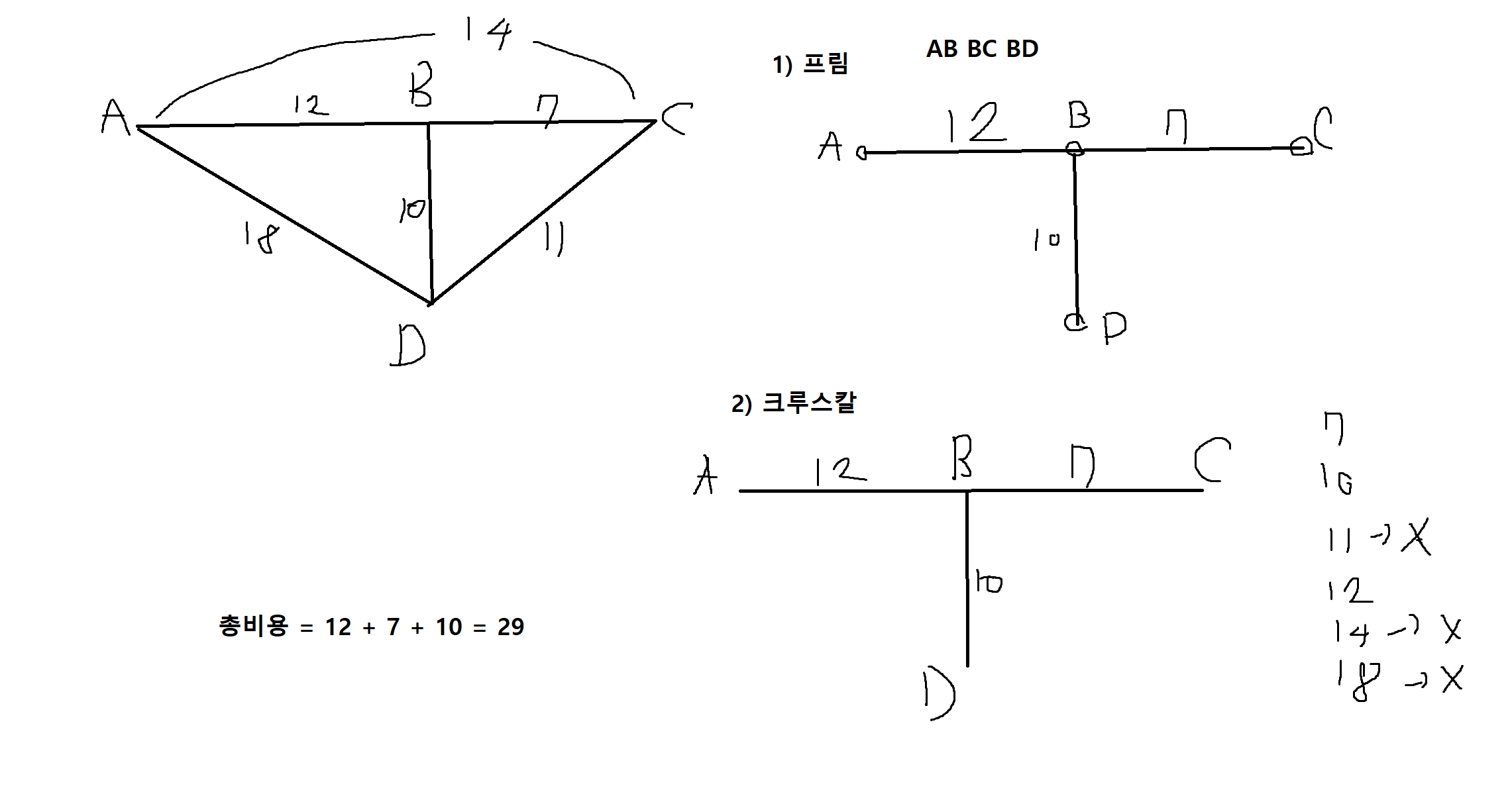
3) 다음 그래프에서 최소비용 생성트리를 a로 시작하는 경우 프림, 크루스칼의 알고리즘을 이용하여 각각 구하고 생성트리의 비용을 나타내시오.

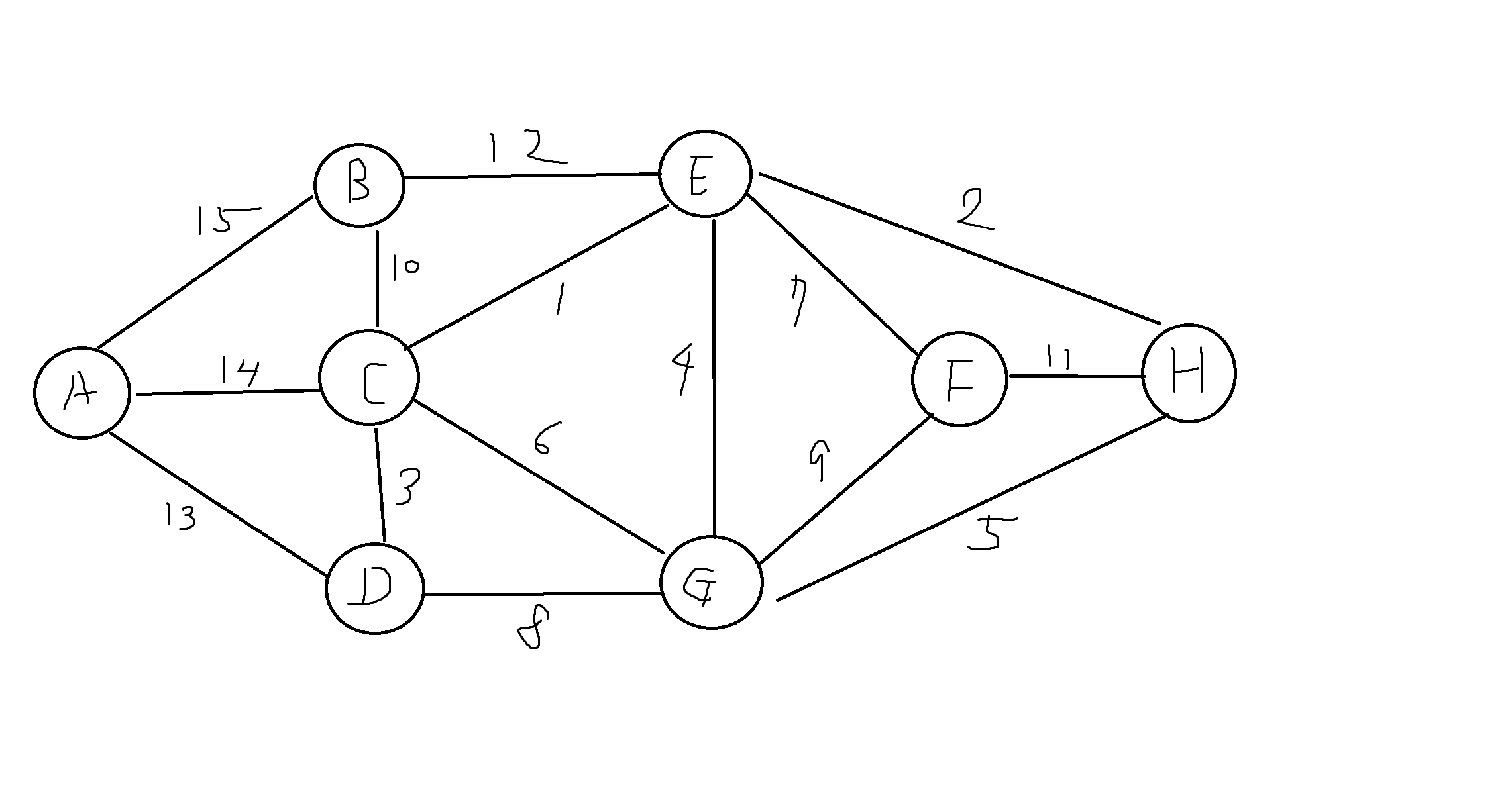
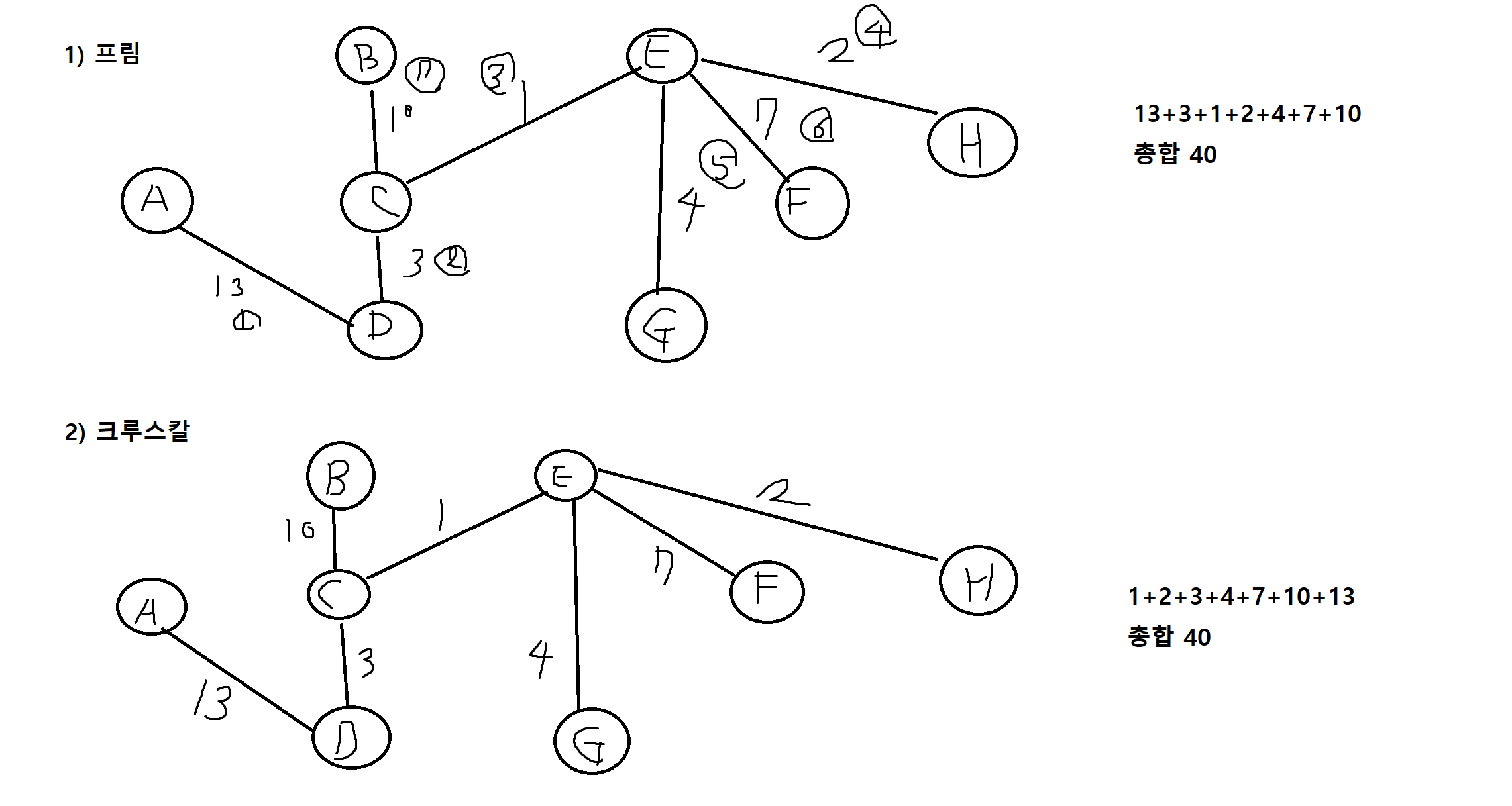
4) 다음 그래프에서 최소비용 생성트리를 a로 시작하는 경우 프림, 크루스칼의 알고리즘을 이용하여 각각 구하고 생성트리의 비용을 나타내시오.

---

트리의 활용 - 문법의 파싱, 하프만 코드, 게임, 결정트리

(1) 문법의 파싱 (Parsing)

• 트리는 문법의 파싱을 통해 자연어처리와 컴파일러(compiler)등에 활용
• 문장 트리에서 문장은 주어, 동사, 목적어로 이루어짐
• 주어는 관사와 명사구로 나누어지고 목적어는 관사와 명사구로 나눠짐
• 명사구는 형용사와 명사로 다시 나누어지는 파싱과정을 반복함

(2) 하프만 코드 (Huffman code)

알파벳의 열(sequence)로서 이루어진 메시지가 있고, 각 메시지의 영문자가 각각 독립적이고 위치에 관계없이 어떤 정해진 확률로 나타남

예를 들어, 5개의 영문자 a, b, c, d, e가 각각 나나탈 확률이 0.12, 0.4, 0.15, 0.08, 0.25라고 할 때, 이 영문자를 각각 0과 1의 열로서 코드화하고자 하면, 어느 영문자의 코드도 다른 어떤 영문자의 코드의 접두어로 표현되어서는 안됨

a가 01이고 b가 010일 때, a는 b의 접두어가 되므로 적합하지 않음

• 하프만 코드 특성을 이용하여 최소 개의 코드로서 정확하게 송신할 수 있으며 수신된 코드를 정확하게 코드화가 가능함

• 접두어 성질을 만족하는 최적의 코드화 방법을 하프만 알고리즘이라고 함

• 그 결과 e와 같이 나타날 확률이 높은 문자는 코드 길이가 짧고, z와 같이 나타날 확률이 작은 문자는 코드길이가 커지는 원리임
  (빈도수를 구하는 것)

영문자	확률	코드1	코드2
a	0.12	000	000
b	0.40	001	11
c	0.15	010	01
d	0.08	011	001
e	0.25	100	10

<그림 8.18> 문자가 나타날 확률과 이진코드의 예

bade -> 001 000 011 100 코드1
11 000 001 10 코드2

(1) 가장 낮은 확률을 가진 두 문자 a,b를 선택하여 가상의 다른 문자 x로 대치한다. x가 나타날 확률은 a와 b의 확률을 합한 것

(2) 위의 과정을 반복하여 최종 확률이 1이 될 때까지 계속한다.

(3) 최종적인 트리가 완성되면 각 서브트리의 왼쪽에는 0을 부여하고, 오른쪽에서 1을 각각 부여하여 각 문자의 코드를 결정한다.

---

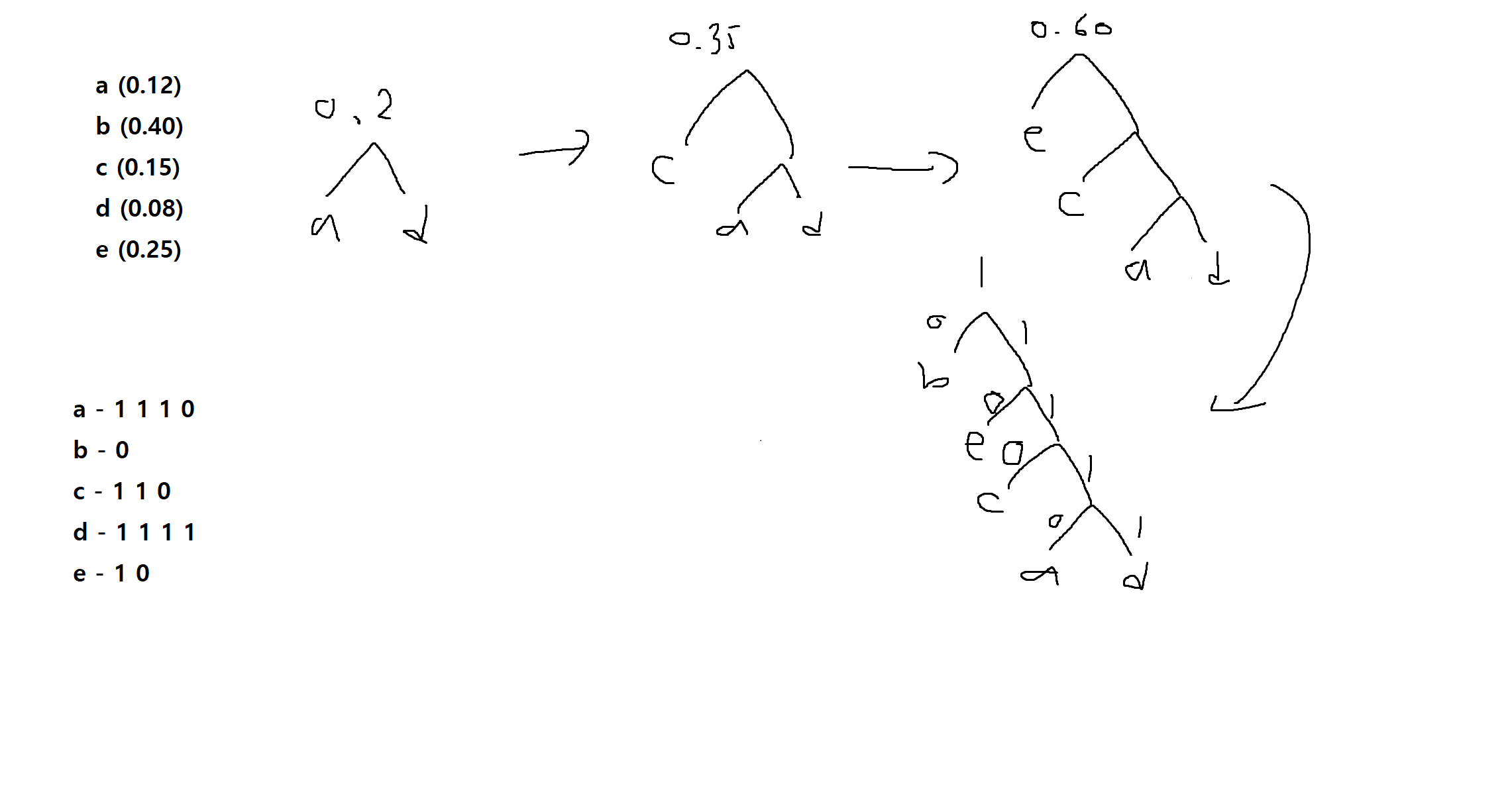
(3) 게임 (game)

• 트리는 체스, 틱택토 (tic-tac-toe), 장기, 바둑 등 게임에 있어서의 진행과 전략을 구사할 수 있는 게임 트리로도 활용됨

• 가로, 세로, 대각선으로 연속된 세 개를 놓으면 이기는 게임인 tic-tac-toe 게임의 일부를 나타냄

• X가 이기면 1, O가 이기면 -1, 무승부면 0
  

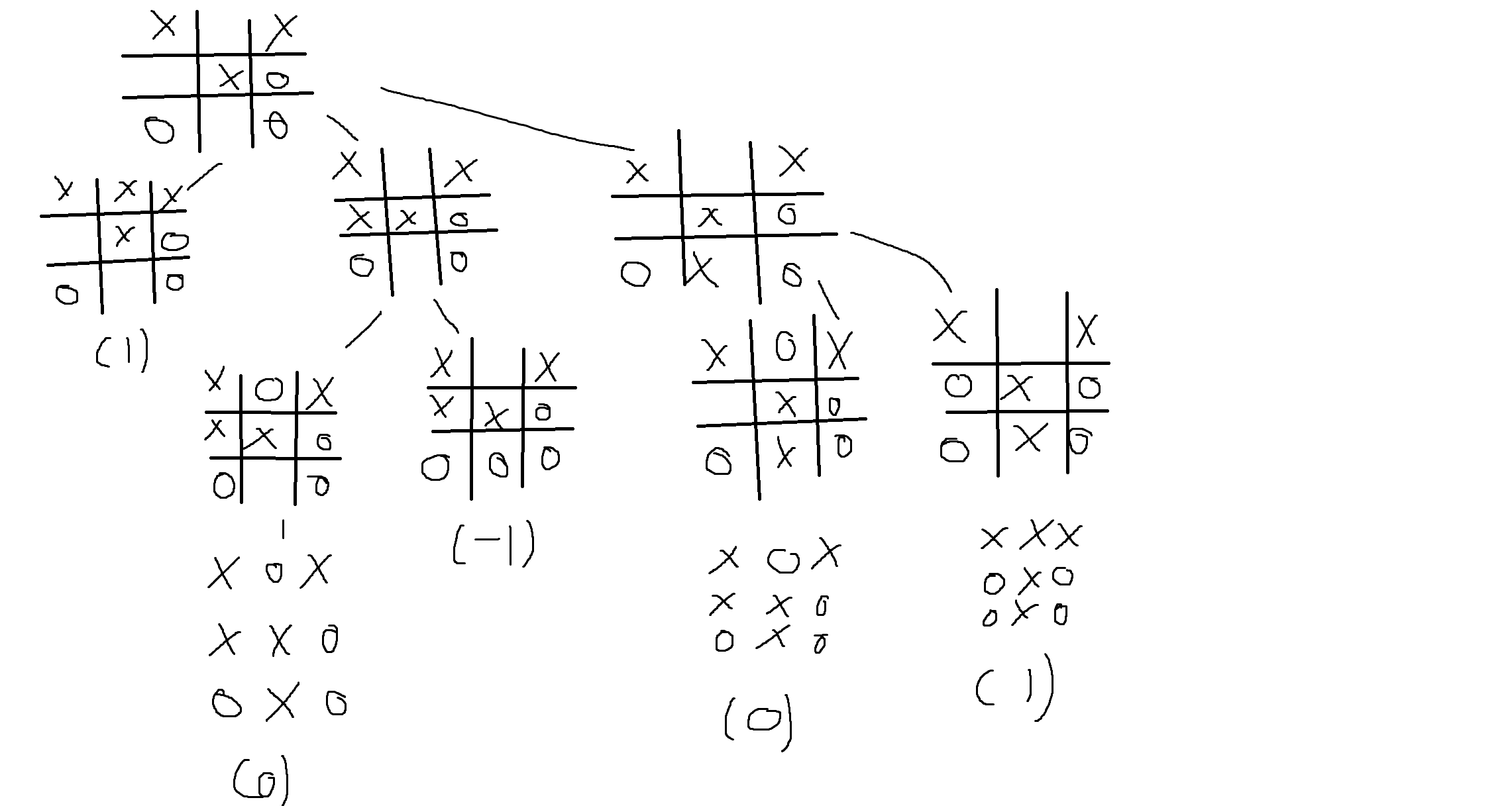
요약

• 트리는 문법의 파싱, 하프만 코드, 결정트리, 게임 등에 활용된다.

연습문제

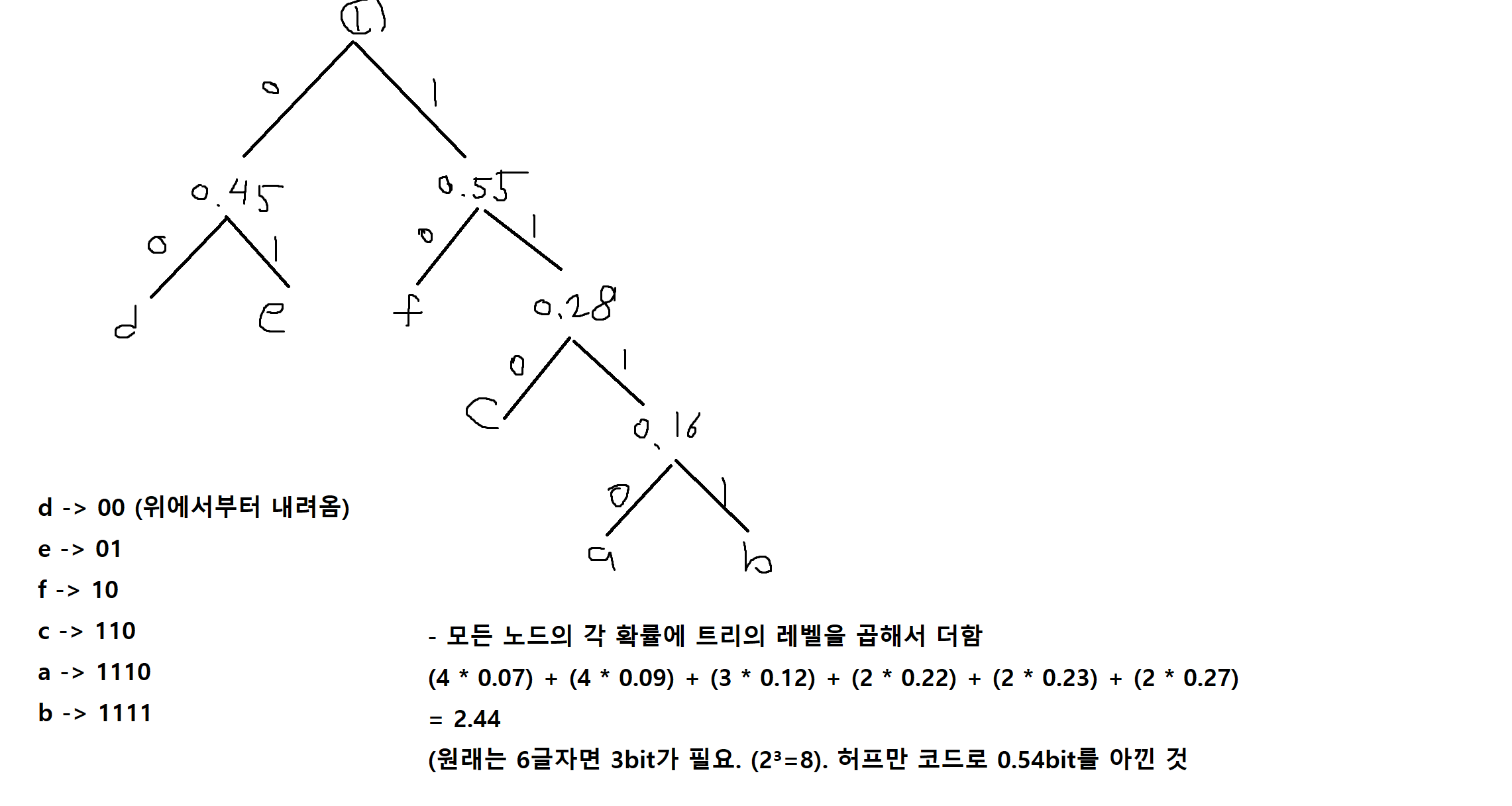
1) 여섯 개의 영문자 a,b,c,d,e,f가 각각 0.07, 0.09, 0.12, 0.22, 0.23, 0.27의 확률을 가진다고 하자. 하프먼 트리를 만들고 최적의 하프먼 코드를 만드시오. 또한 그 코드의 평균길이를 구하시오. (확률이 더 낮은 것을 왼쪽에 놓고 0을 부여함)
(작은 것부터 합치며 왼쪽에 0, 오른쪽에 1)

순서)
1. 가장 작은것 2개를 합침. 해당 2개는 없애고 합친 값을 전체에 넣음
2. 다시 가장 작은 것 2개를 합침. 해당 2개 없애고 합친 값을 전체에 넣음
3. 반복

---

결정트리, 트리의 응용

결정트리 (decision tree)

• 트리를 이용할 때 매우 유용하게 쓰이는 것이 결정트리임

• 가능성이 있는 경우의 수가 너무나 많기 때문에 모든 면에서 입증하기가 어려운 문제를 만날 수 있음

• 결정트리를 활용하면 주어진 문제를 일목요연하게 입증할 수 있음

8개의 동전문제

• 결정트리의 예로 잘 알려짐

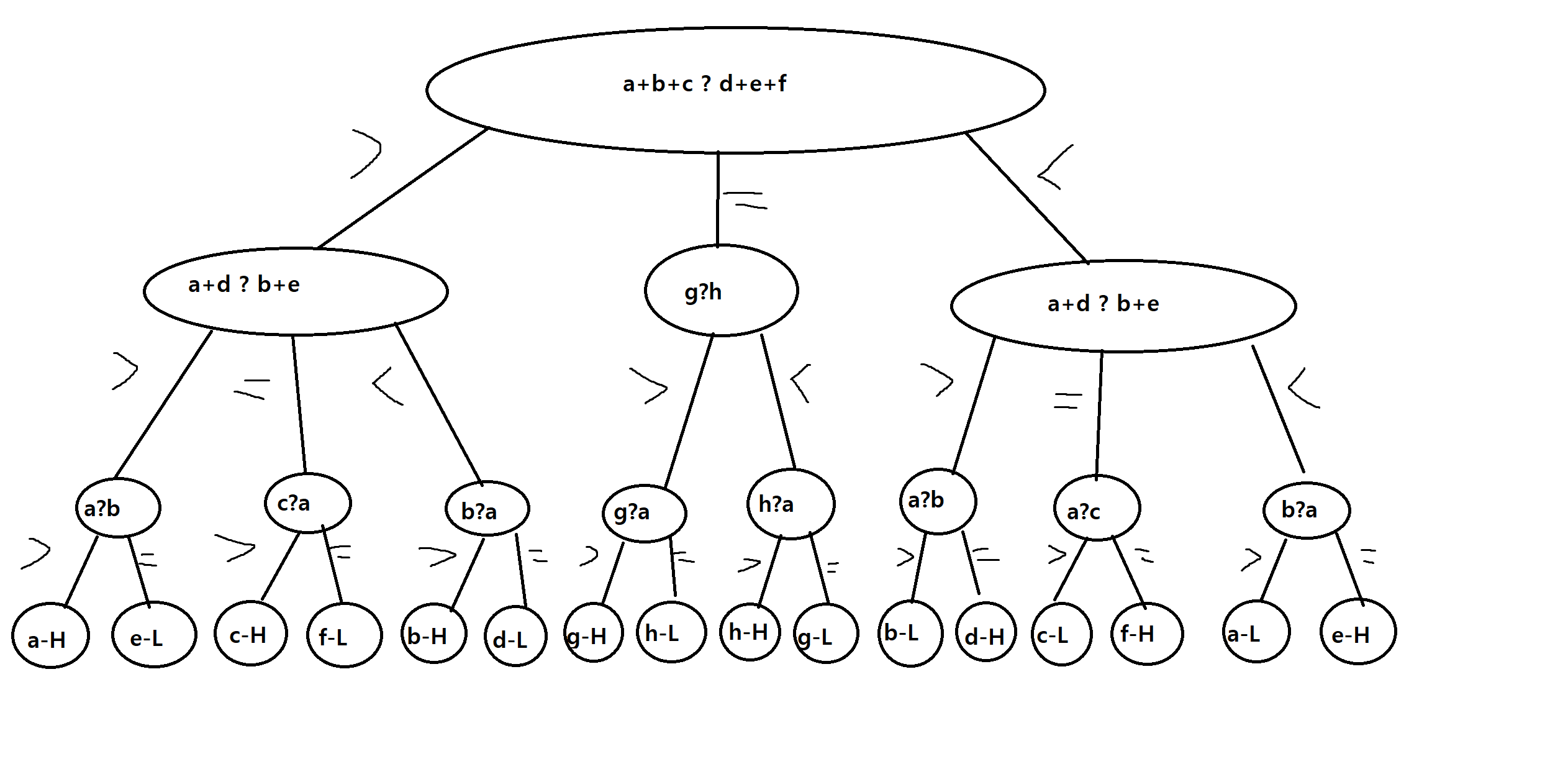
• 크기와 색깔이 똑같은 동전 a,b,c,d,e,f,g,h 중에서 한개가 불량품이어서 다른 동전들과 다른 무게를 가짐

• 무게가 같거나 크고 작은 것만을 판단할 수 있는 하나의 천칭.
  저울을 사용하여 단 세번만의 계량으로 어느 동전이 불량품이고,
  다른 동전보다 무겁거나 가벼운지를 동시에 판단하려고 함

• a+b+c < d+e+f 일 경우 불량품이 (a,b,c,d,e,f) 6개 중에 있으며 g와 h는 정상품이라는 것을 알 수 있다.
  

• 다음 단계에서 d와 b를 저울에서 바꾸어 계량한 결과 a+d < b+e로 부등호에 변화가 없다면 2가지 가능성 (b,c,d,f는 정상품이고 a(L)나 e(H)가 불량품)을 말해줌

• 최종판단을 위한 프로시저인 comp의 프로그램임

• 프로시저 eight-coins는 앞의 결정트리의 판단과 같은 기능을 수행함

void comp(int x, int y, int z)
/* x를 정상품인 y와 비교한다 */
{
	if (x>z)
    	printf("%d heavy \n", x);
    else
    	printf("%d light \n", y);
}
/* comp * /

연습문제

2) 8개의 동전 문제 결정트리에서 (가)와 (나)의 경우는 어떤 것을 유추할 수 있는지 설명하시오. 즉, 어떤 동전의 불량품 가능성과 그 동전이 다른 정상품보다 무거운지 가벼운지 설명하시오.

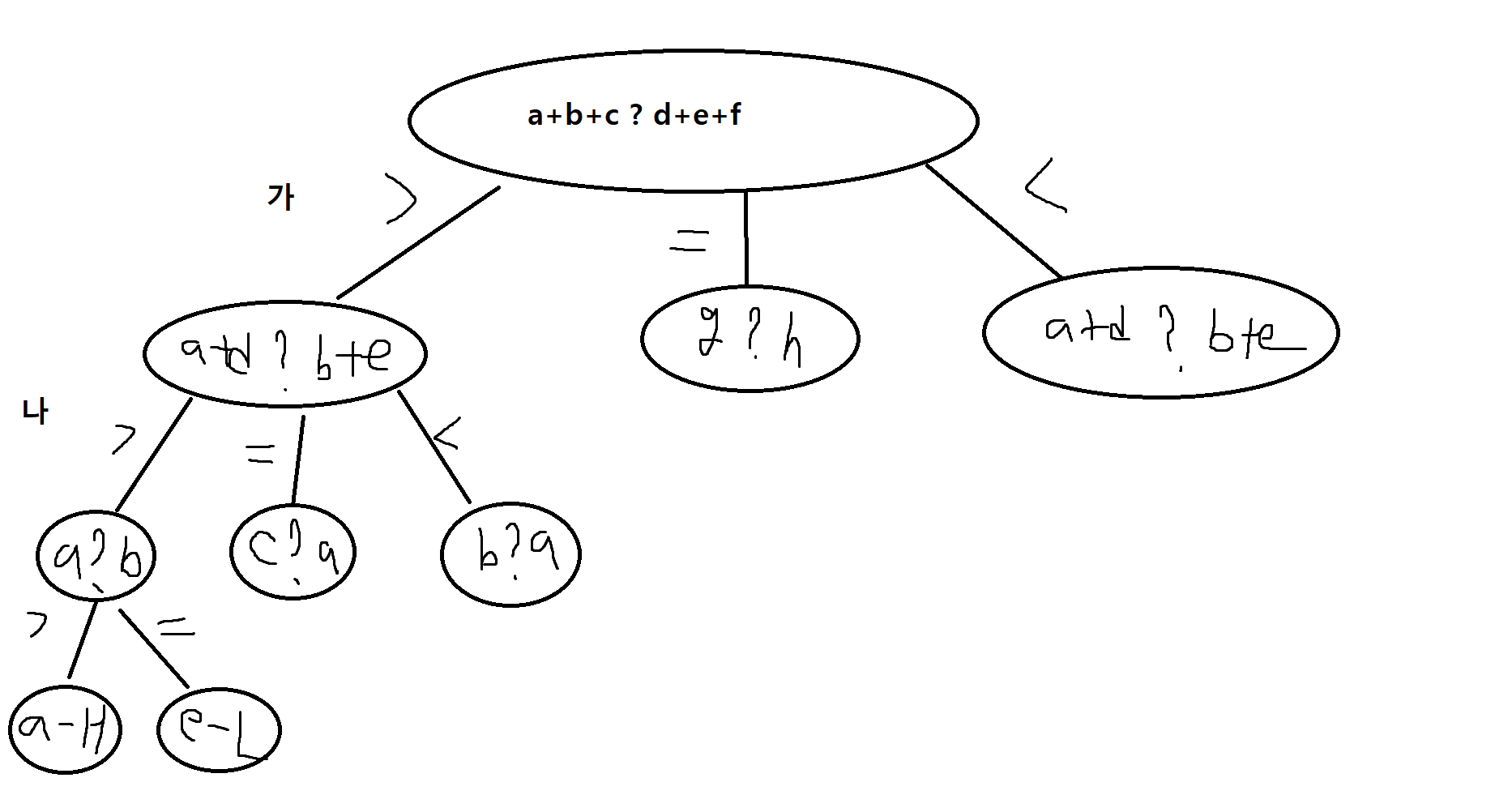
가 -> a+b+c 중에 불량품이 있고 무거운 불량품이다
나 -> a+d 중에 무거운 불량품이 있을 수도 있고, b+e 중에 가벼운 불량품이 있을 수 도 있다.