부울대수
-> 참 또는 거짓 (1, 0)으로 표현
- 부울식은 두 원소를 가지는 집합 A = {0, 1}과 이항연산자 (binary operator) + (or) 와 * (and) 그리고 단항 연산자(unary operator), complement로 표현되는 식을 말함
1) + (or) :
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 1
2) (and)
0 0 = 0
0 1 = 0
1 0 = 0
1 * 1 = 1
3) ' (not)
0' = 1
1' = 0
- 부울식에서 연산자의 연산 우선순위는 ' > * < + 순이다.
0 1 + 1 1 + 0' 1'
= 0 1 + 1 1 + 1 0
= 0 + 1 + 0
= 1
예제 11-1
(1) 0 + 1'
0 + 0 = 0
(2) 0 0 + 1' 0
0 0 + 0 0 = 0
(3) (1 + 0') 1
(1 + 1) 1 = 1
(4) (1 0 + 0 1)' + 0' 0'
(0 + 0)' + 1 1
1 + 1 = 1
정의 11-1. 부울식은 다음과 같이 정의된다.
1) 상수 0과 1 그리고 부울 변수는 부울식이다.
2) f1과 f2가 부울식 일 떄 f₁', f₁+ f₂, f₁* f₂(f₁) 역시 부울식이다.
부울변수가 x,y,z라 할 때 정의에 따라 다른 식들은 부울식이 된다.
x' + yz + (x + y + z)'
0 + (xy)' + (x' + zy)
-
부울식에서 부울변수 x,y,z가 가질 수 있는 값인 0 또는 1을 전해줌으로써 각 부울식에 대한 값을 구할 수 있음
-
두 부울식이 같은 진리표 (truth table)을 가질 경우 두 부울식을 동치(equivalent)라 함
-
두 함수 f1과 f2가 동치일 경우 f1 = f2 로 표시함
부울식의 법칙
p, q, r을 부울변수라 한다.
-
멱등법칙
p * p = p
p + p = p -
항등법칙
p + 0 = p
p * 1 = p -
교환법칙
p + q = q + p
p q = q p -
결합법칙
p + (q + r) = (p + q) + r
p (q r) = (p q) r -
분배법칙
p + (q r) = (p + q) (p + r)
p (q + r) = (p q) + (p * r) -
흡수법칙
p + (pq) = p (하나가 1이면 1, 1+(1q) = 1) (0 + (0 q) = 0)
p (p+q) = p -
역법칙
p + p' = 1
p * p' = 0 -
보법칙
(p')' = p -
우등법칙
p + 1 = 1
p * 0 = 0 -
드모르간 법칙
(p+q)' = p' * q'
(pq)' = p' + q'
예제 11-2. p, q, r이 부울변수일 때 부울식 (p+q')' * r' = p'qr'이 성립함을 보여라
(p+q')' * r' = (p'q) r' = p'qr'
(드모르간), (보법칙)
예제 11-3.
(1) x + xy
x + xy 1
x(1 + y) -> 1+y는 1
x 1 = x
(2) wy + xy + wz + xz
(w + x)y + (w + x)z -> 분배법칙
(w + x)(y+z) -> 분배법칙
예제 11-4. 다음 부울식이 성립함을 진리표를 이용하여 살펴보자.
x+yz = (x+y)(x+z)
| x | y | z | yz | x+y | x+z | (x+y)(x+z) | x+yz |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
두 값이 같다.
부울변수들에 대한 함수를 부울함수라 하며, n개의 부울변수 x₁,x₂,... xn에 대한 부울함수는 f(x₁,x₂,... xn)으로 표시함
부울함수로 표시하면
f(x,y) = x + xy
f(x,y,w,z) = wy +xy + wz + xz
(오른쪽에 없는게 왼쪽에 들어가면 안됨)
부울함수 (Boolean function)
-
부울변수와 부울 연산자로 구성된 부울식으로 표현할 수 있음
-
n개의 부울변수가 있을 때 그 변수들로부터 얻을 수있는 조합은 00...0, 00...1, ... 11...1로 x개임
-
0은 그에 해당하는 원소가 없는 경우임
-
1은 있는 경우로 생각함
정의 11-2. n개의 부울변수로 만들어지는 진리표에서 변수의 각 합을 최소항(Min term)이라고 한다.
변수가 n개면 최소항은 2^n개
변수 2개 -> 2² = 4개
| 00 | x'y' |
| 01 | x'y |
| 10 | xy' |
| 11 | xy |
예제 11-5. x=1, y=0, z=1일 때 부울함수 f(x,y,z)의 값은 1이 되고, 다른 경우에는 0의 값을 가진다고 하자. 이때 그 부울함수에 대한 진리표를 구하고, f(x,y,z) = 1인 최소항을 부울변수의 곱으로 나타내어보자.
변수 3개 -> 2³ = 8
| x | y | z | f |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
f(x,y,z) = xy'z
예제 11-6. 부울변수에 대한 진리표가 다음과 같을 때 부울함수 f(x,y,z)를 구해보자
| x | y | z | f(x,y,z) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
f(x,y,z) = x'y'z + xy'z' + xyz'
-
곱의 합 (Sum of products) 또는 논리합 표준형은 부울함수를 나타내는데 있어서 최소항들의 합으로 표현하는 것임
-
최소항들은 부울변수의 곱으로 표현됨
-
부울함수는 부울변수의 곱의 합으로 표현됨
예제 11-7. 다음의 부울함수를 부울변수의 곱의 합으로 나타내어보자
(1) f(x, y) = x' + y
| x | y | x' | x'+y |
|---|---|---|---|
| 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 |
f(x,y) = x'y' + x'y + xy
(2) f(x,y,z) = (x+y) * z'
| x | y | z | x+y | z' | (x+y) * z' |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 | 0 |
f(x,y,z) = x'yz' + xy'z' + xyz'
-
부울변수의 최소합들로부터 얻어진 부울함수는 좀 더 간단한 형태의 식으로 만들 수 있음
-
간단한 형태의 식이란 같은 기능이나 결과를 도출하면서도 더 작은 변수와 이산자를 사용한 식을 말함
-
부울 함수식을 간소화하는 방법
(1) 부울식의 기본법칙 사용
(2) 카노우맵을 사용 -
부울식의 법칙을 이용하여 부울함수를 간소하게 하는 방법은 부울식의 기본법칙을 이용하는 것으로, 그 과정이 복잡하고 간소화에 대한 확인이 쉽지 않음
예제 11-8. 다음 부울함수를 부울식의 기본법칙을 이용하여 간단하게 해봐라.
f(x,y,z) = x'y'z' + x'yz' + xy'z' + xyz'
x'z'(y'+y) + xz'(y'+y)
= (x'z' + xz') * (y'+y)
= z'(x' + x) = z'
정의 11-3. 카노우맵은 부울변수들에 대한 최소합들을 도표로 그린 후 인접한 최소항들을 서로 묶어서 표현함으로써 부울함수를 간소화하는 방법이다.
연습문제
1)
가) (1+0)' + (0+1)
= 1' + 1 = 1
나) (0+1)' + (1+1)' + 0' 1'
= 1' + 1' + 1 0
= 0
2) 다음 부울식에 해당하는 진리표를 만드시오
(x+y')x
| x | y | y' | x+y' | (x+y')x |
|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 |
3) 다음의 부울식을 부울식의 기본 법칙을 이용하여 간단히 하시오.
wx + (x'z)' + (y+z')
= wx + (x+z') + (y+z')
= (wx + x) + (y+z'+z') -> (z'+z'=z')
= x(w+1) + (y + z') -> w+1 = 1
= x + y + z'
(세부적인 설명)
wx + ((x')' + z') + (y + z') -> 드모르간
= wx + (x + z') + (y + z') -> 보
= (wx + x) + z' + (y + z') -> 결합
= x(w + 1) + z' + (y + z') -> 분배
= x + z' + (y + z') -> 흡수
= x + (z' + z') + y -> 결합
= x + z' + y -> 멱등
4) 다음의 진리표에서 부울함수를 곱의 합으로 나타내고, 기본법칙을 이용하여 간단히 하시오.
| a | b | c | f(a,b,c) |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
f(a,b,c) = a'b'c' + a'bc + ab'c' + abc
= b'c'(a'+a) + bc(a'+a)
= b'c' + bc
카노우맵
-
카노우맵을 그릴 때는 부울변수들로부터 나타내어지는 모든 경우의 최소합들을 사각형으로 연결시켜서, 최소항들 중 1의 값을 가지는 사각형 안에 '1'을 표시함
-
'1'로 표시된 사각형들에서 부울식의 공통점을 찾아내어 부울함수를 간소화하는데, 사각형을 연결시킬때는 인접한 사각형끼리는 한 변수의 변화만 있게 만들어야 함
-
예를 들어 x와 y가 부울변수일 때 xy와 x'y'는 두 변수 모두 다른 값을 가지기 때문에 서로 인접하지 않음
xy -> x'y' (X)
xy -> x'y (O)
xy -> xy' (O)
(1) 두 변수에 대한 카노우맵
두 변수를 x와 y라 할 때, 그에 필요한 사각형은 변수들이 가질 수 있는 모든 경우인 x'y', x'y, xy', xy에 대한 것임
| x,y | 0 | 1 |
|---|---|---|
| 0 | x'y' | x'y |
| 1 | xy' | xy |
-
x가 0이고 y가 0일 때는 그에 해당하는 부울식은 x'y'가 됨
-
다른 사각형들도 그 위치에 따라 부울식의 값이 정해짐
-
예를 들어 f(x,y) = x'y' + x'y + xy'일 경우 이 함수를 카노우맵으로 나타내면
| x,y | 0 | 1 |
|---|---|---|
| 0 | 1 | 1 |
| 1 | 1 |
-
카노우맵의 사각형에 해당하는 논리값이 1이면 '1'로 표시, 0이면 그냥 공백으로 남겨둠
-
'1'로 표시된 사각형이 인접할 경우, 그들을 함께 묶어서 표현하는 방법은 다음과 같다.
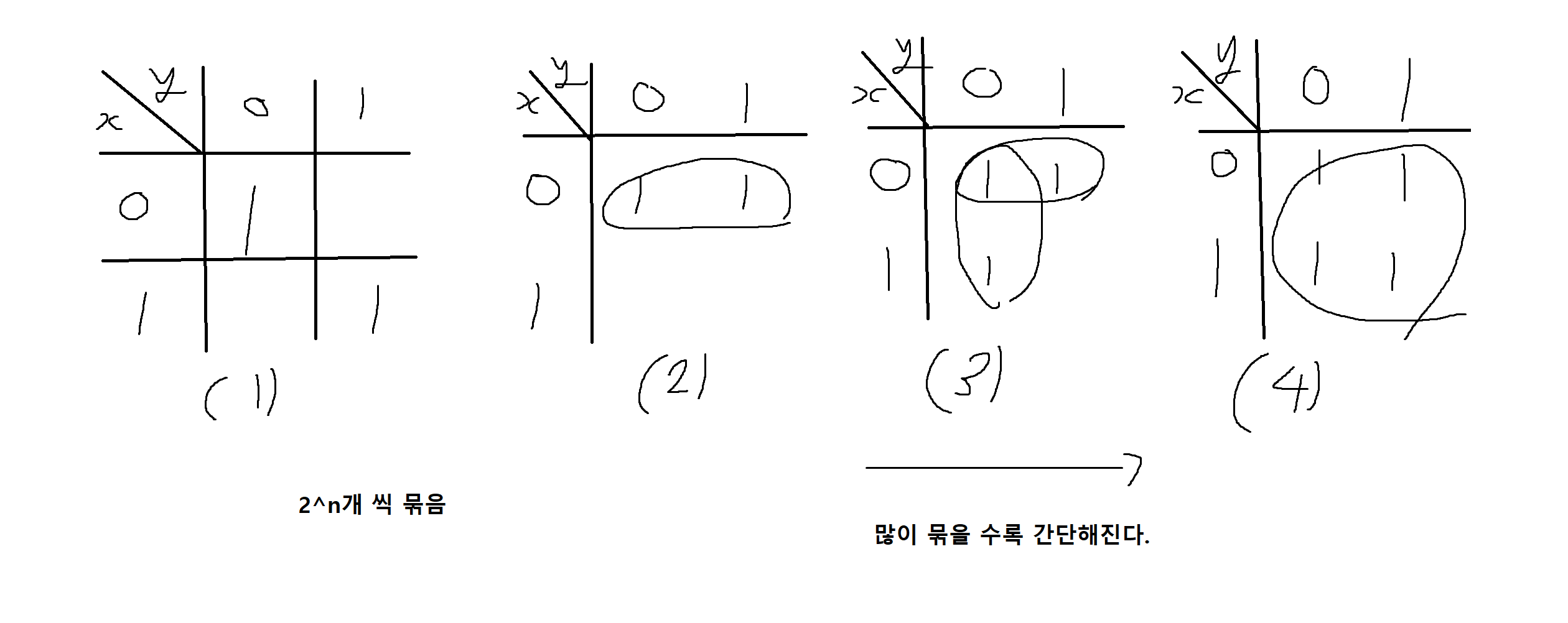
(1)의 경우에는 서로 인접한 1이 없어서 묶을 수 없으므로 각각 따로 표현하면 x'y' + xy가 됨
(2) y의 값이 0이든 1이든 관계없이 x의 값이 0일 때, 다시 말해 x'일 때 1의 값을 가지므로 x'가 됨
(3) 윗 부분의 묶음은 (2)의 경우와 같고, 아랫쪽으로의 묶음은 x의 값과 관계없이 y'이므로, 부울식은 x' + y'가 된다.
(4) x와 y의 값에 관계없이 항상 1이므로 부울식은 1이 됨
(3)을 부울식의 기본법칙으로 간소화하려면 중복으로 묶인 최소항을 중복으로 써주면 됨
x'y' + x'y + x'y' + xy' = x'(y'+y) + y'(x'+x) = x' + y'
예제 11-9. 다음 부울함수에 대한 카노우맵을 그린 후 간소화해보자.
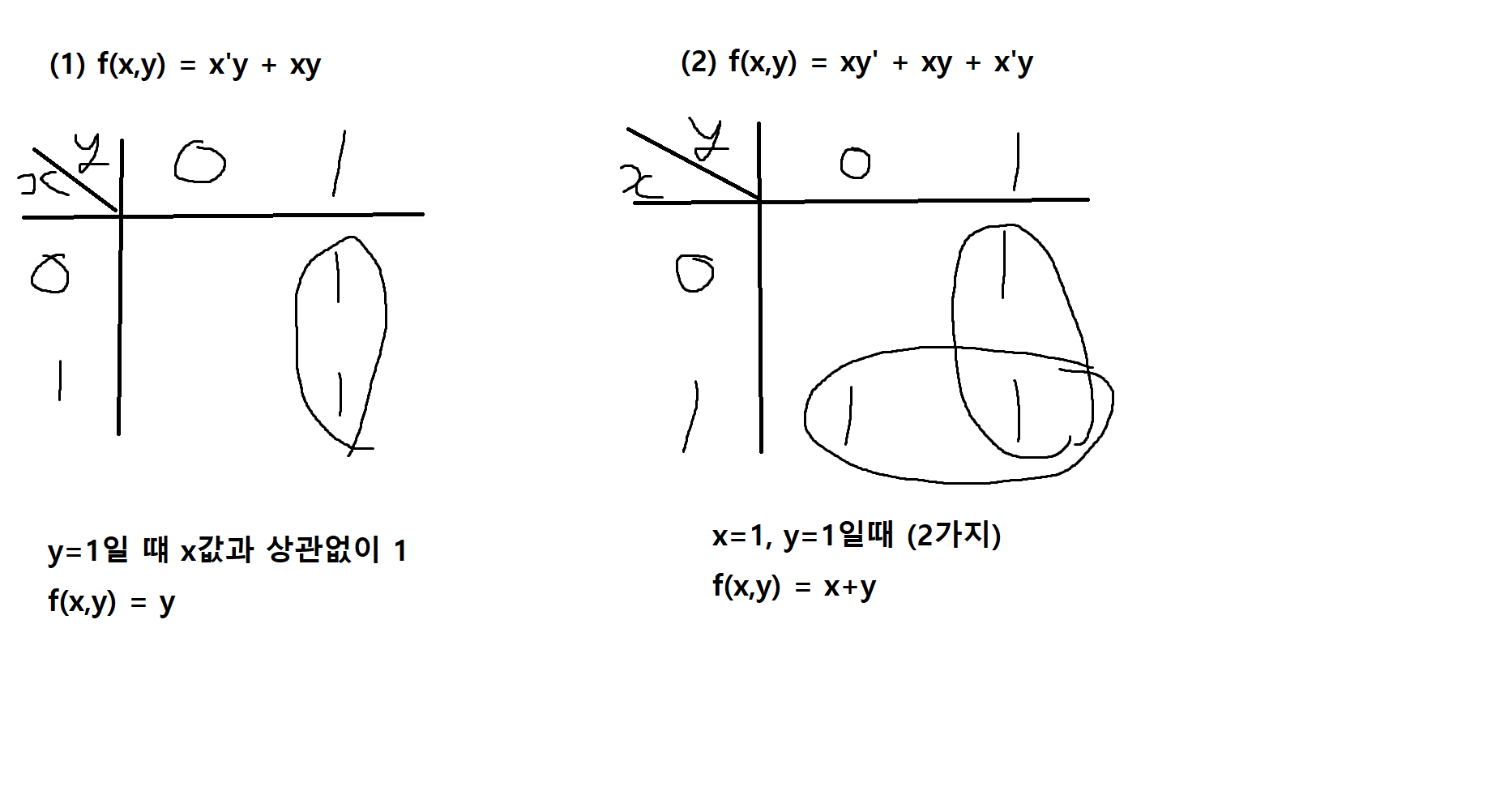
(2) 세 변수에 대한 카노우맵
-
변수가 세 개인 경우에는 2³=8개의 사각형이 필요함
-
세 변수에 대한 카노우맵 그림은 아래와 같음
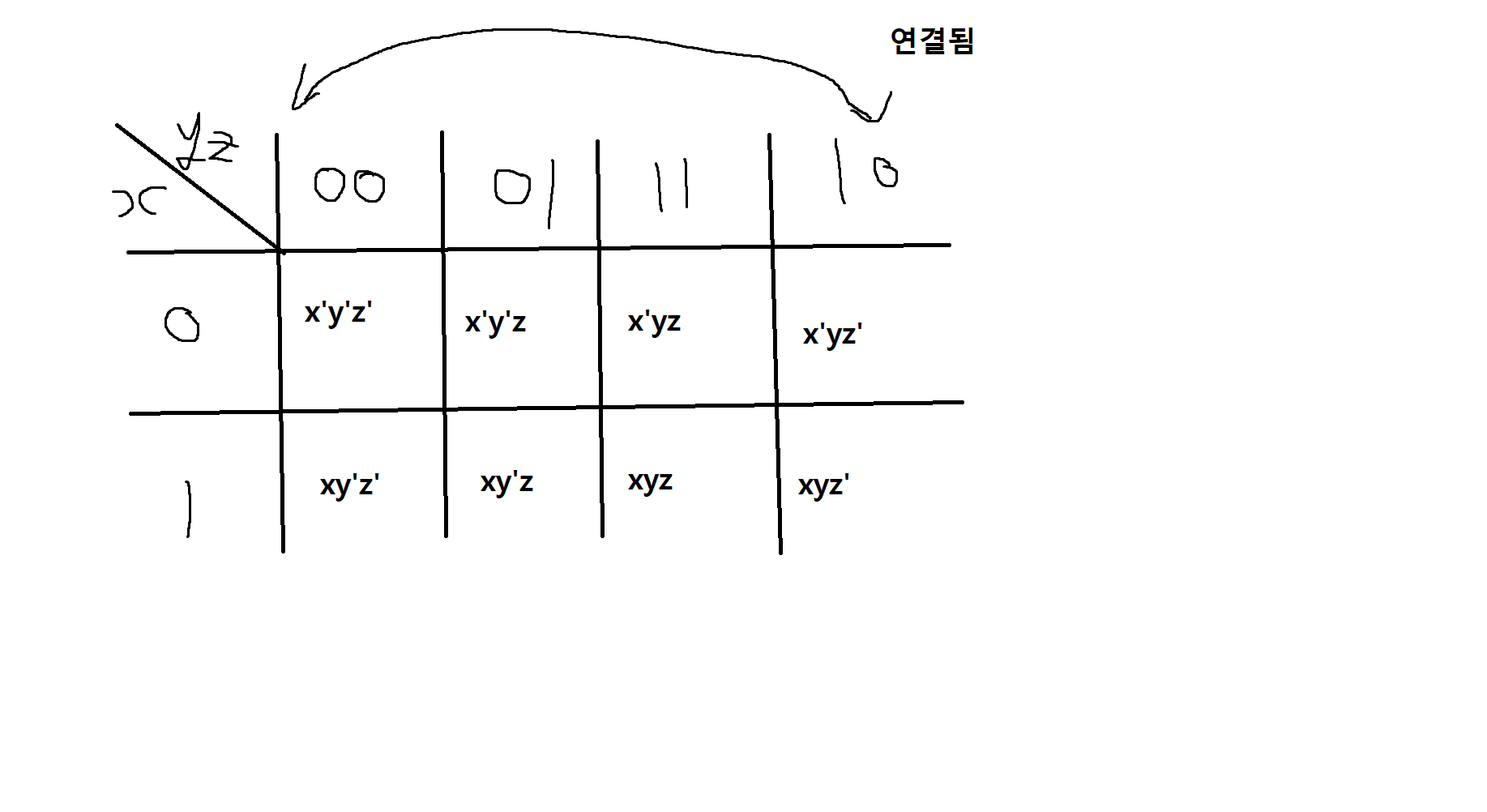
세 변수에 대한 카노우맵을 그릴때 유의해야 할 사항
-
yz에 대한 사각형에서 오른쪽 방향으로 00, 01 다음에 10이 아니라 11이라는 것
-
두 변수가 한꺼번에 변하는 것은 인접할 수 없기 때문에 이 옆에는 10이 아닌 11이 옴
-
왼쪽 끝의 사각형들을 오른쪽 끝의 사각형들과 인접되어 있다고 생각해야 함
예) 카노우맵이 아래 그림과 같은 경우 서로 연결되어 있다고 생각하므로 4개의 사각형을 1개로 묶어서 표시하면 z'가 됨
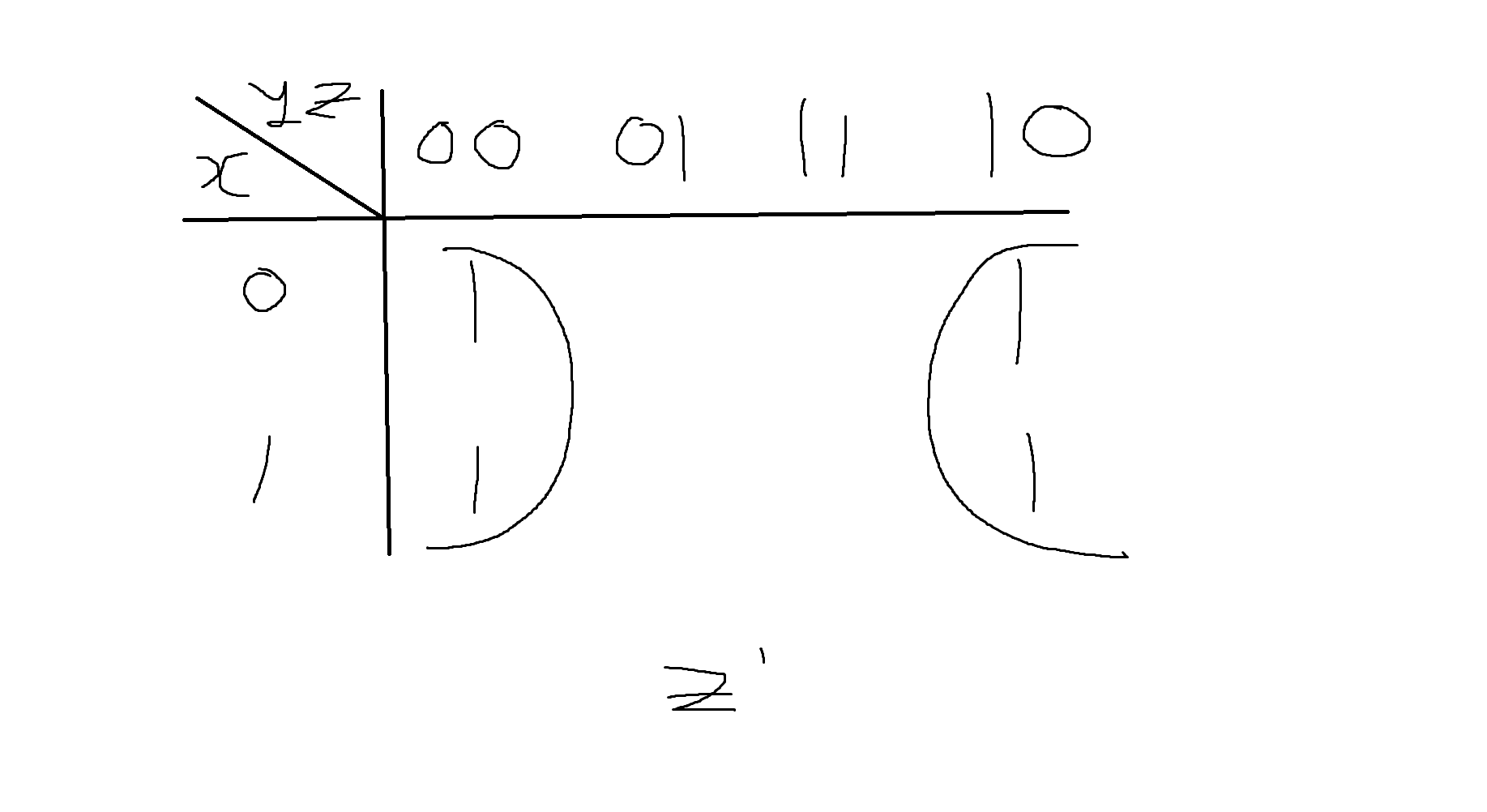
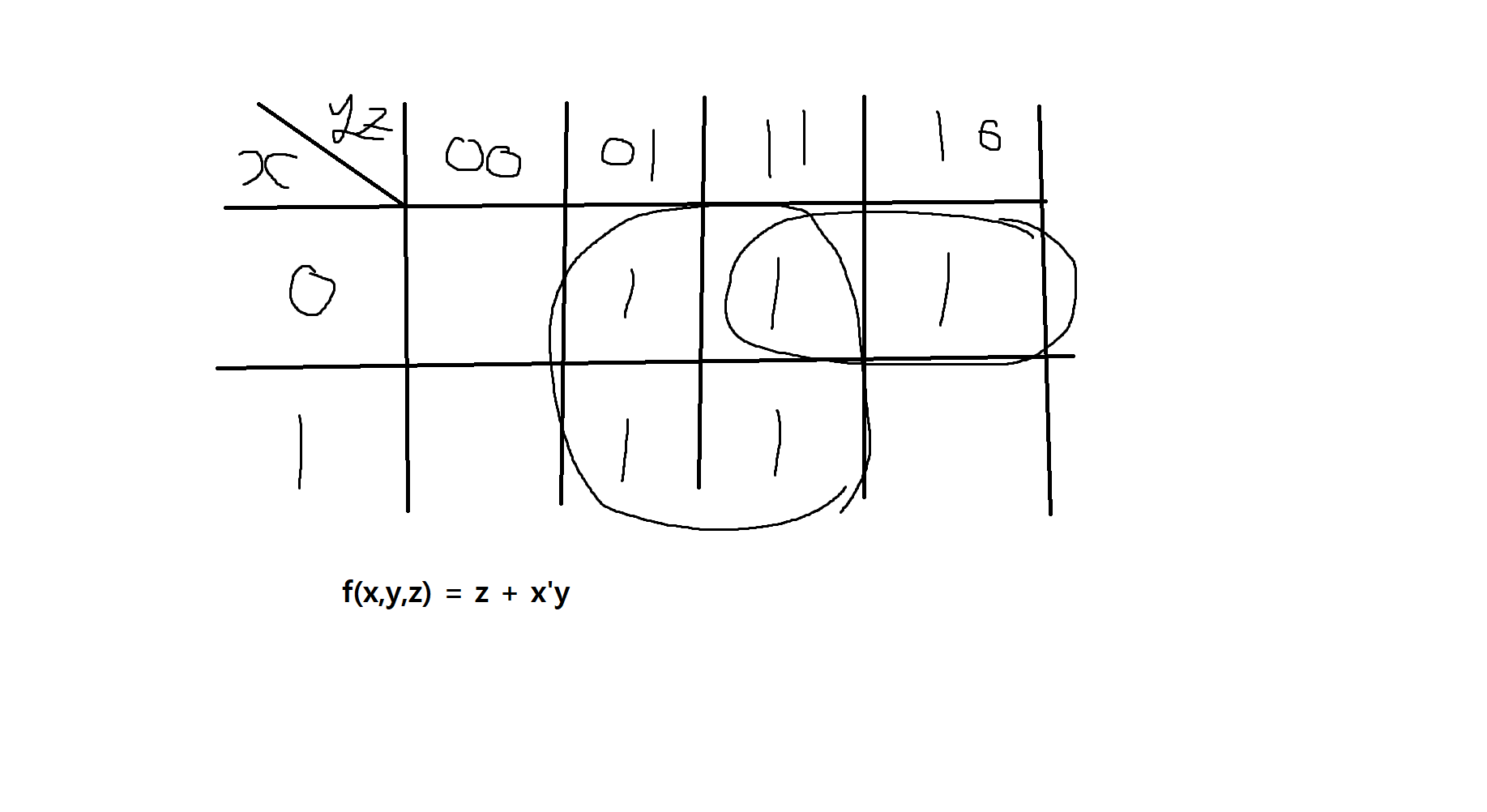
예제 11-10. 다음의 진리표를 보고 카노우맵을 사용하여 부울함수를 간소화해보자.
| x | y | z | f(x,y,z) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
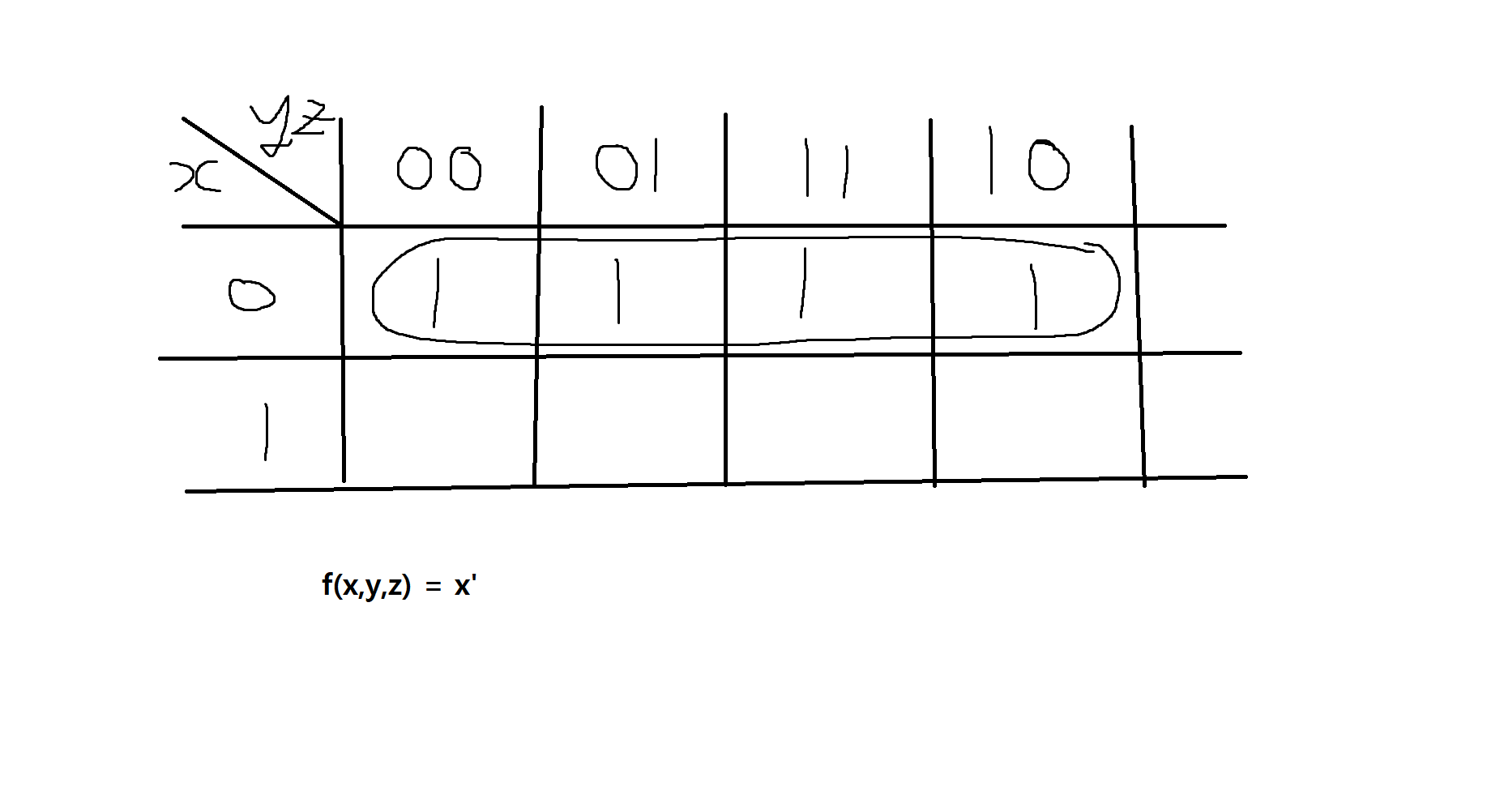
예제 11-11. 다음 부울식을 카노우맵을 사용하여 간소화해보자.
x'y'z' + x'yz'+ x'y'z + x'yz
(3) 네 변수에 대한 카노우 맵
-
네 변수에 대한 카노우맵도 세 변수에 대한 카노우맵과 같이 가로와 세로축에 01 다음에 11이 옴
-
왼쪽 끝과 오른쪽 끝 사각형들이 인접하고 있다고 보며, 위쪽과 아랫쪽 사각형들 역시 인접하고 있다고 봄
| xy,zw | 00 | 01 | 11 | 10 |
|---|---|---|---|---|
| 00 | x'y'z'w' | x'y'z'w | x'y'zw | x'y'zw' |
| 01 | x'yz'w' | x'yz'w | x'yzw | x'yzw' |
| 11 | xyz'w' | xyz'w | xyzw | xyzw' |
| 10 | xy'z'w' | xy'z'w | xy'zw | xy'zw' |
예제 11-12. 카노우 맵을 사용하여 다음 부울함수를 간소화해보자
f(x,y,z,w) = x'y'z'w' + x'y'zw' + x'yz'w + x'yzw + xyz'w + xyzw + xy'z'w'+ xy'zw'
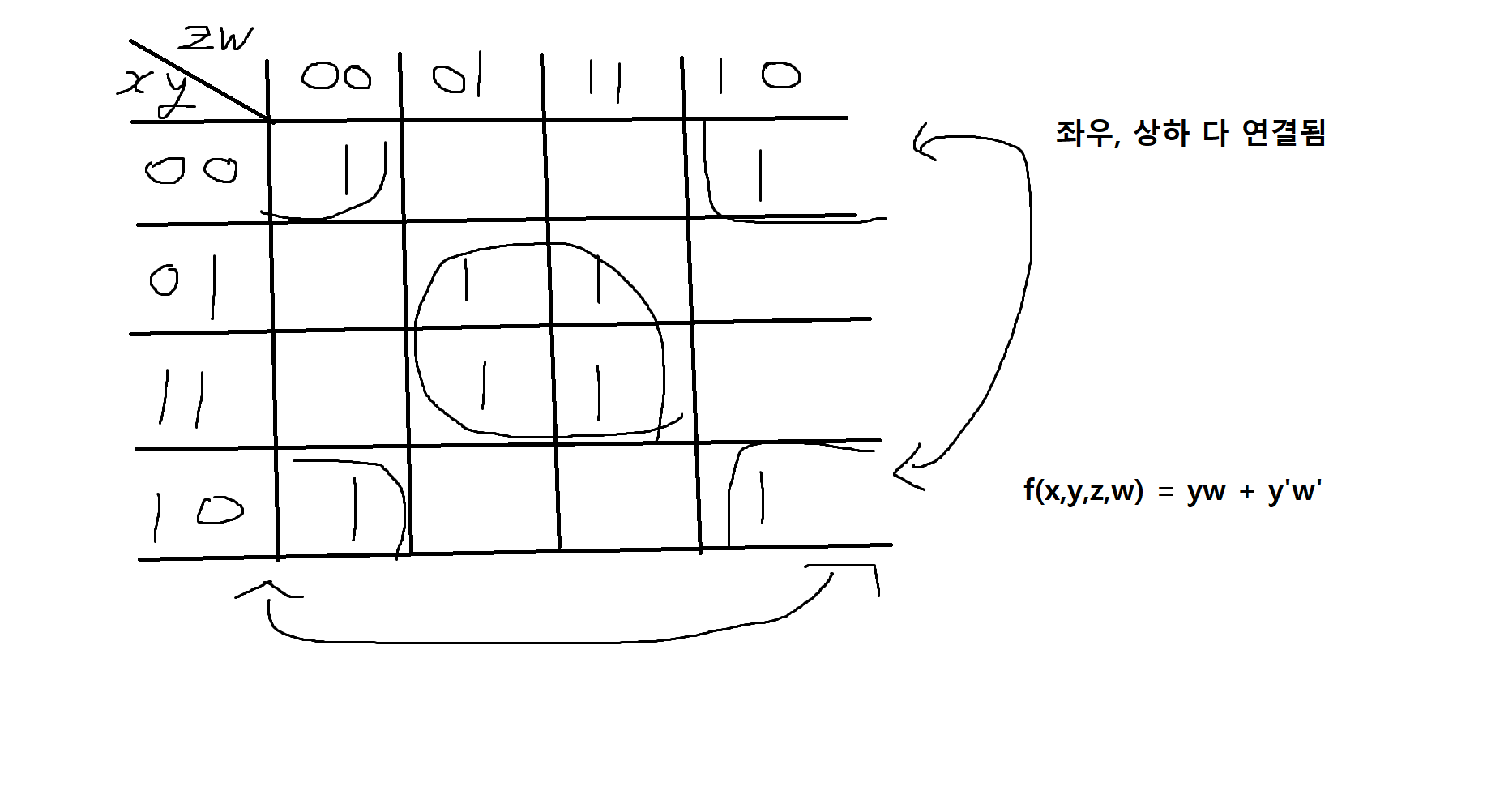
예제 11-13.
카노우맵
1) 2^n 개씩 묶는다.
2) 중복되도 상관없다.
3) 한번에 많이 묶을 수록 간단해진다.
| x | y | z | w | f(x,y,z,w) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
f(x,y,z,w) = xw + xyz'
연습문제
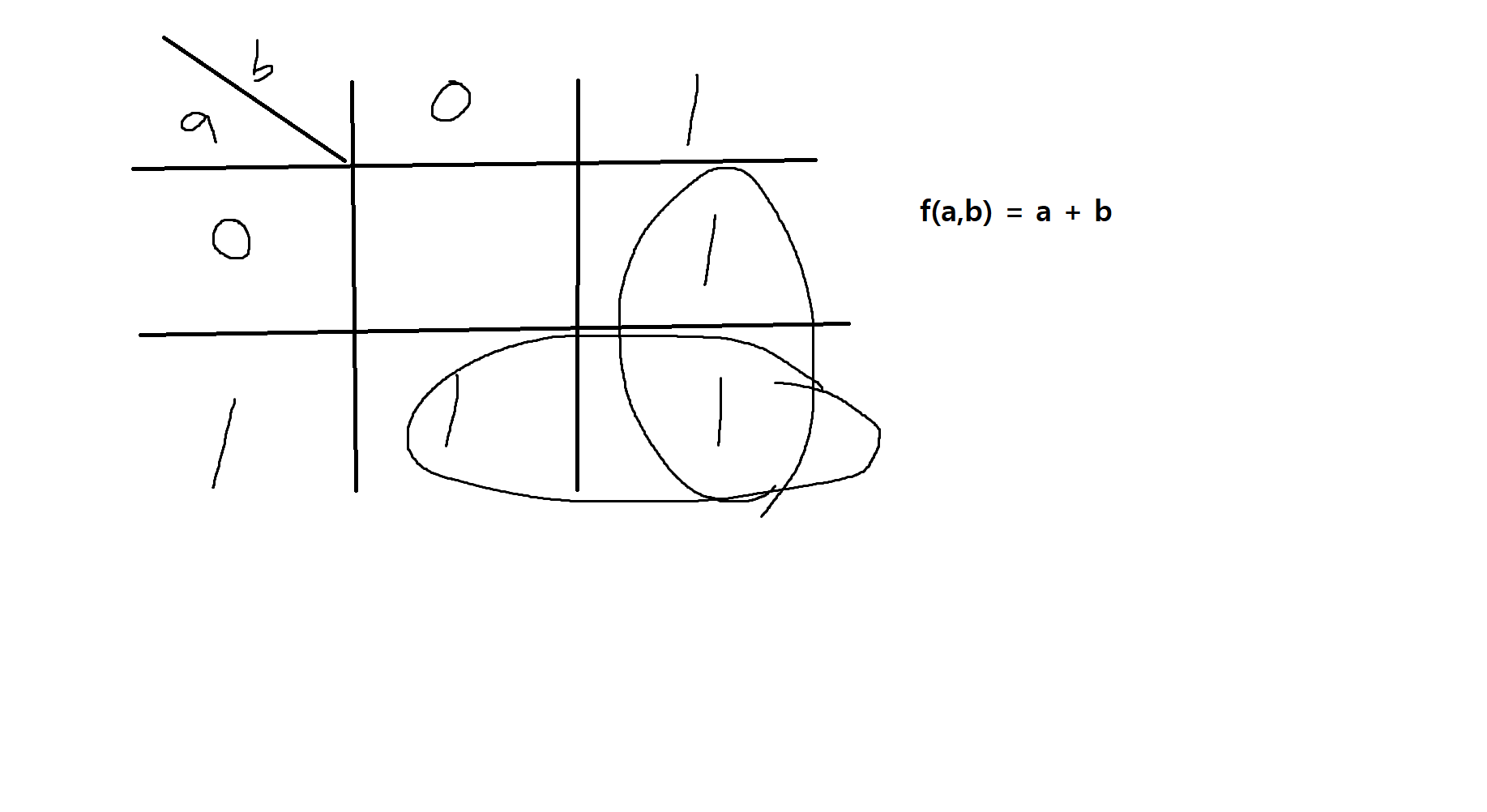
1) f(a,b) = ab' + a'b + ab인 부울함수를 카노우맵을 사용하여 간소화하시오
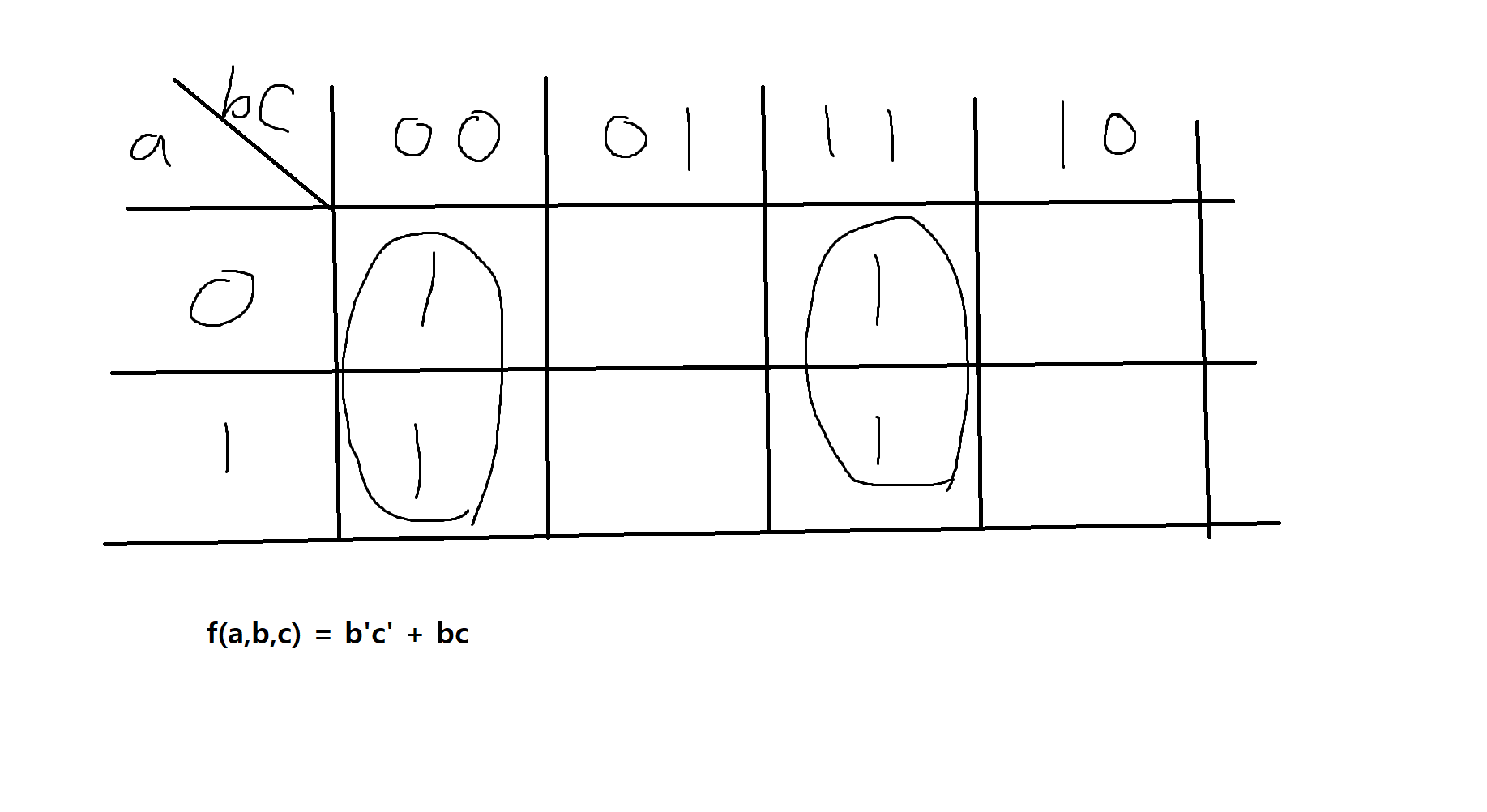
(2) f(a,b,c) = a'b'c' + a'bc + ab'c' + abc 인 부울함수를 카노우맵을 사용하여 간소화하시오.
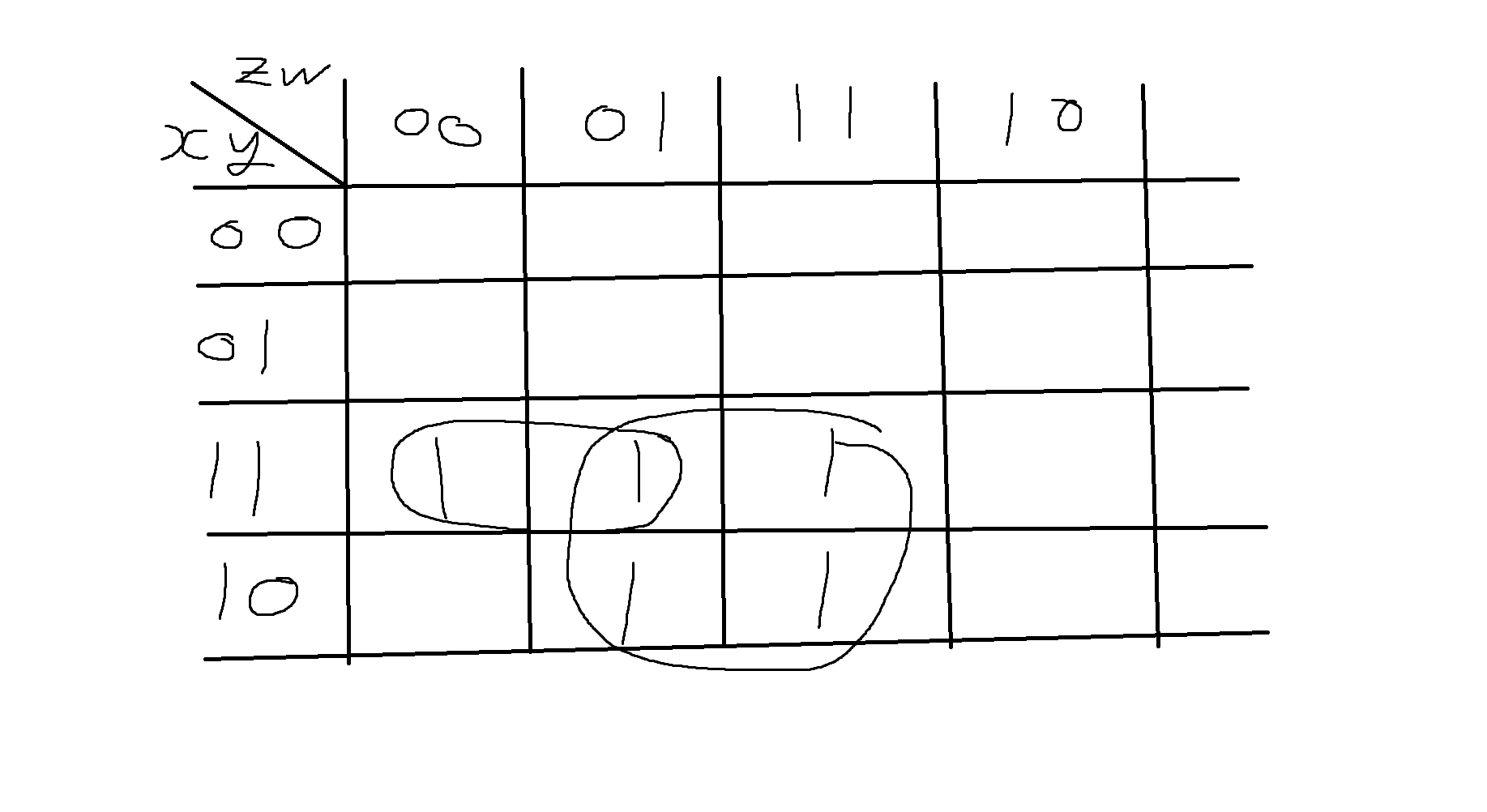
3) 다음의 카노우맵을 보고 간소화된 부울변수 f(x,y,z,w)를 구하시오.
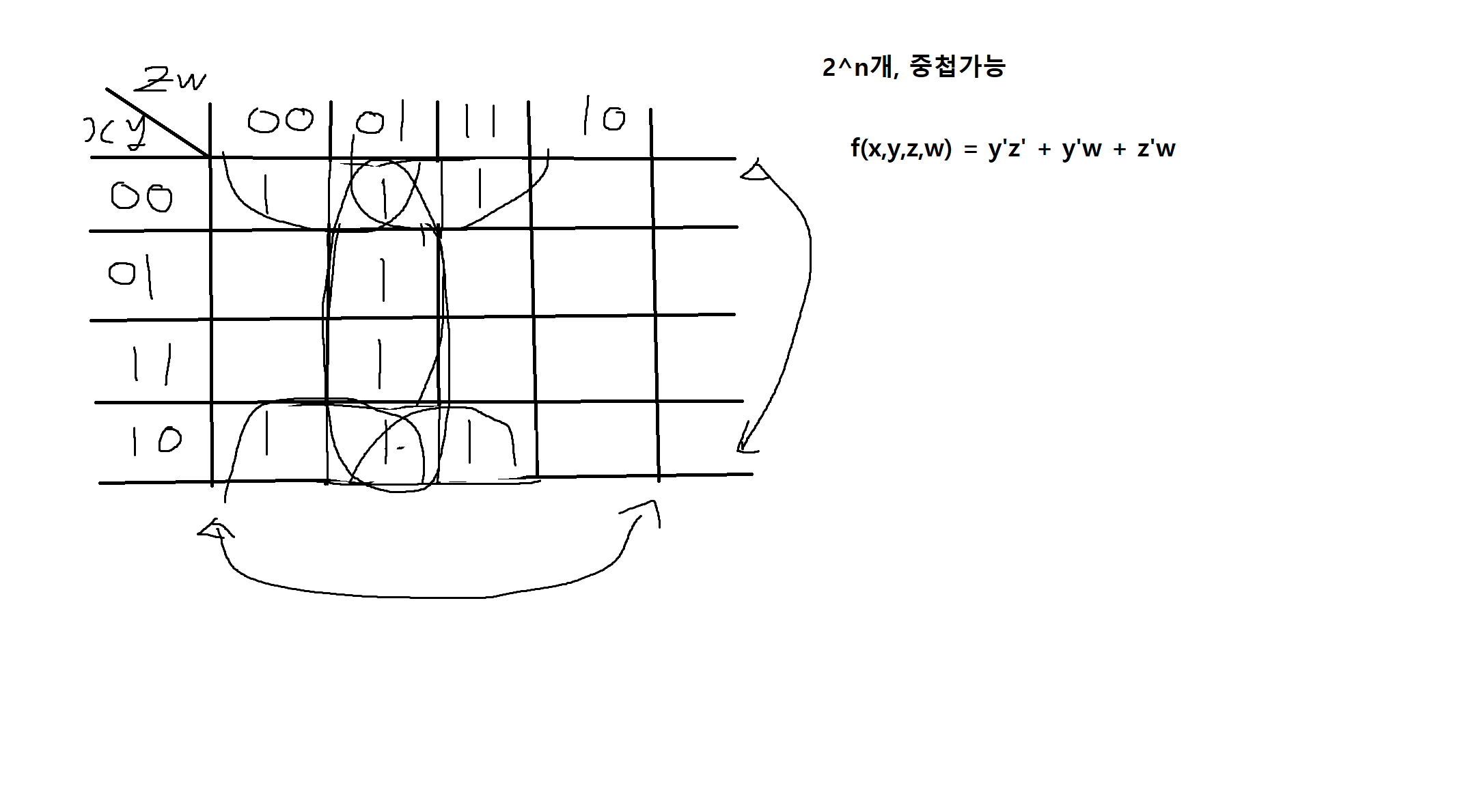
4) 다음의 카노우맵을 보고 간소화된 부울변수 f(x,y,z,w)를 구하시오.
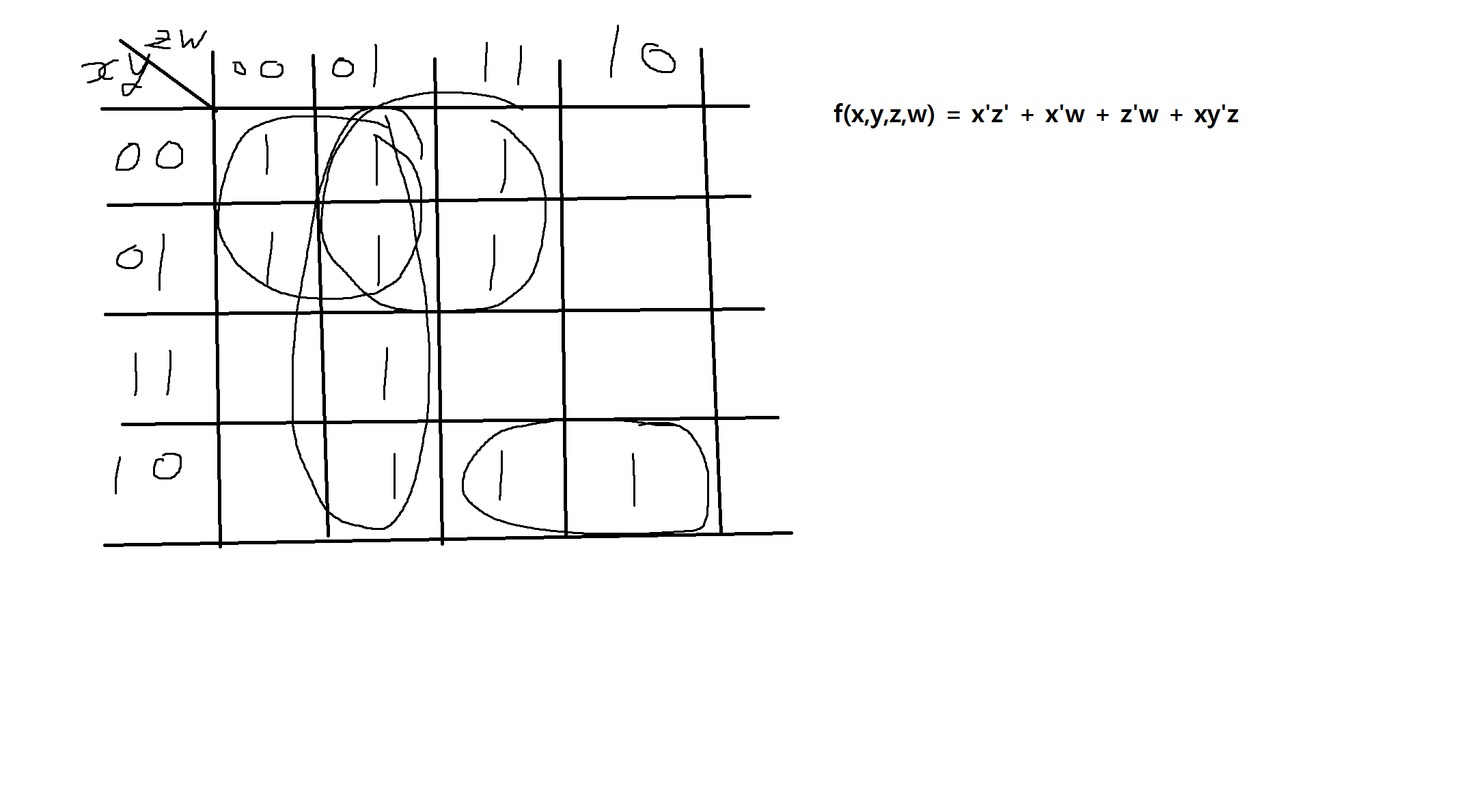
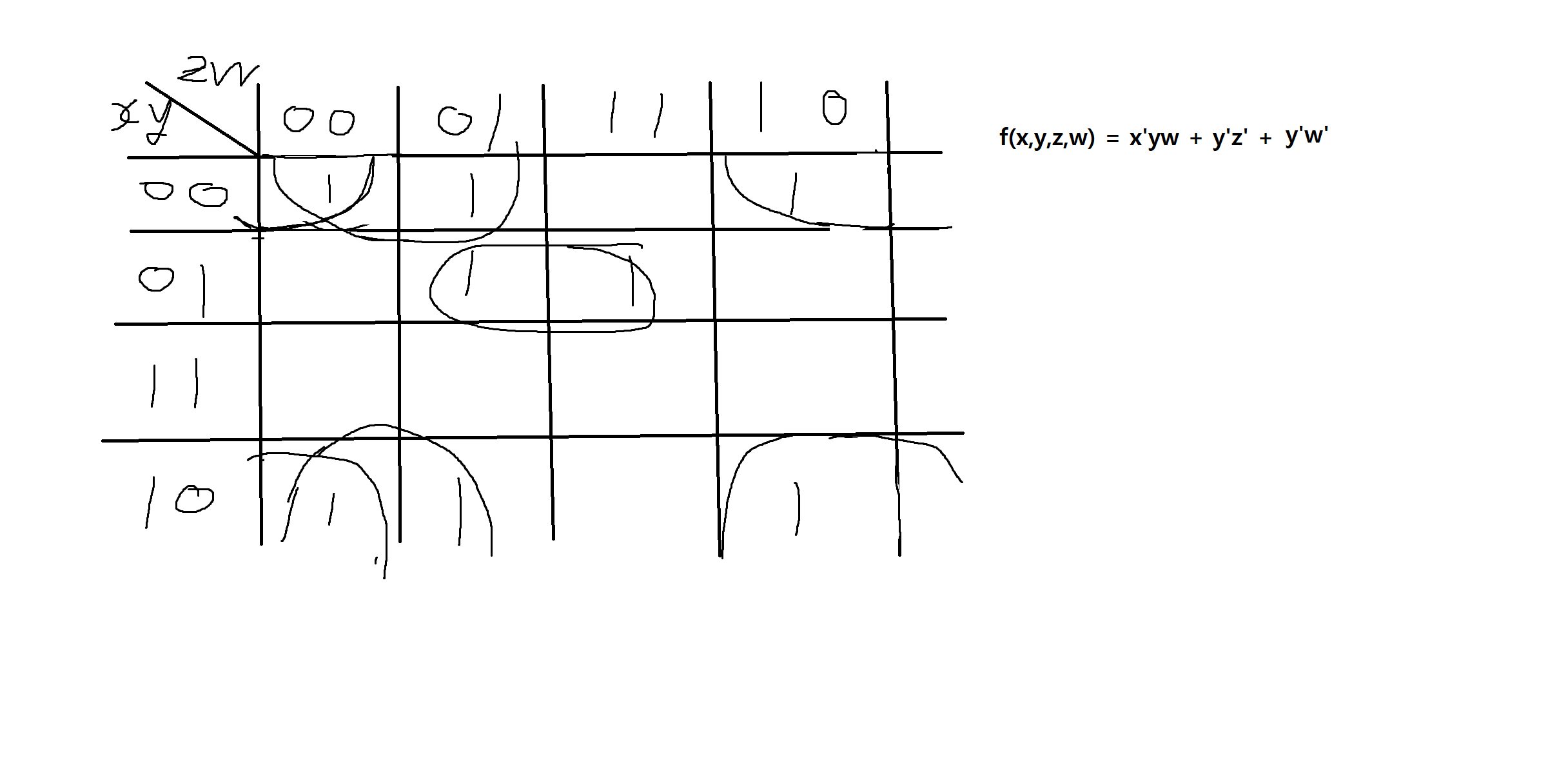
5) f(x,y,z,w) = x'y'z'w' + x'y'z'w + x'y'zw' + x'yz'w + x'yzw + xy'z'w' + xy'z'w + xy'zw'
인 부울함수를 1. 부울식의 기본법칙과 2. 카노우맵을 사용하여 간소화하자.
-
기본법칙
x'y'z'(w'+w) + y'zw'(x'+x) + x'yw(z'+z) + xy'z'(w+w')
= y'z'(x+x') + y'zw' + x'yw
= y'z' + x'yw + y'zw' -
카노우맵
논리회로설계
-
부울함수로 표현된 식은 컴퓨터에서 사용되는 기본적인 논리회로를 설계하는데 활용
-
컴퓨터회로를 설계하는데 있어서 입력과 출력을 논리회로의 게이트(gate)들을 상호연결함으로써 구성할수 있음
-
입력을 부울변수로, 출력을 부울함수로, 부울연산자는 게이트로 표현함
-
논리값이 1일때는 최고의 스위치가 연결된 (on) 상태이고, 0일때는 연결되지 않은(off)상태를 나타냄
(1) 논리곱회로 (AND Gate)
- 2개의 입력 A, B가 모두 1인 경우에만 출력 Y가 1이 됨
- *로 표현
- 두개의 스위치가 모두 1일 때
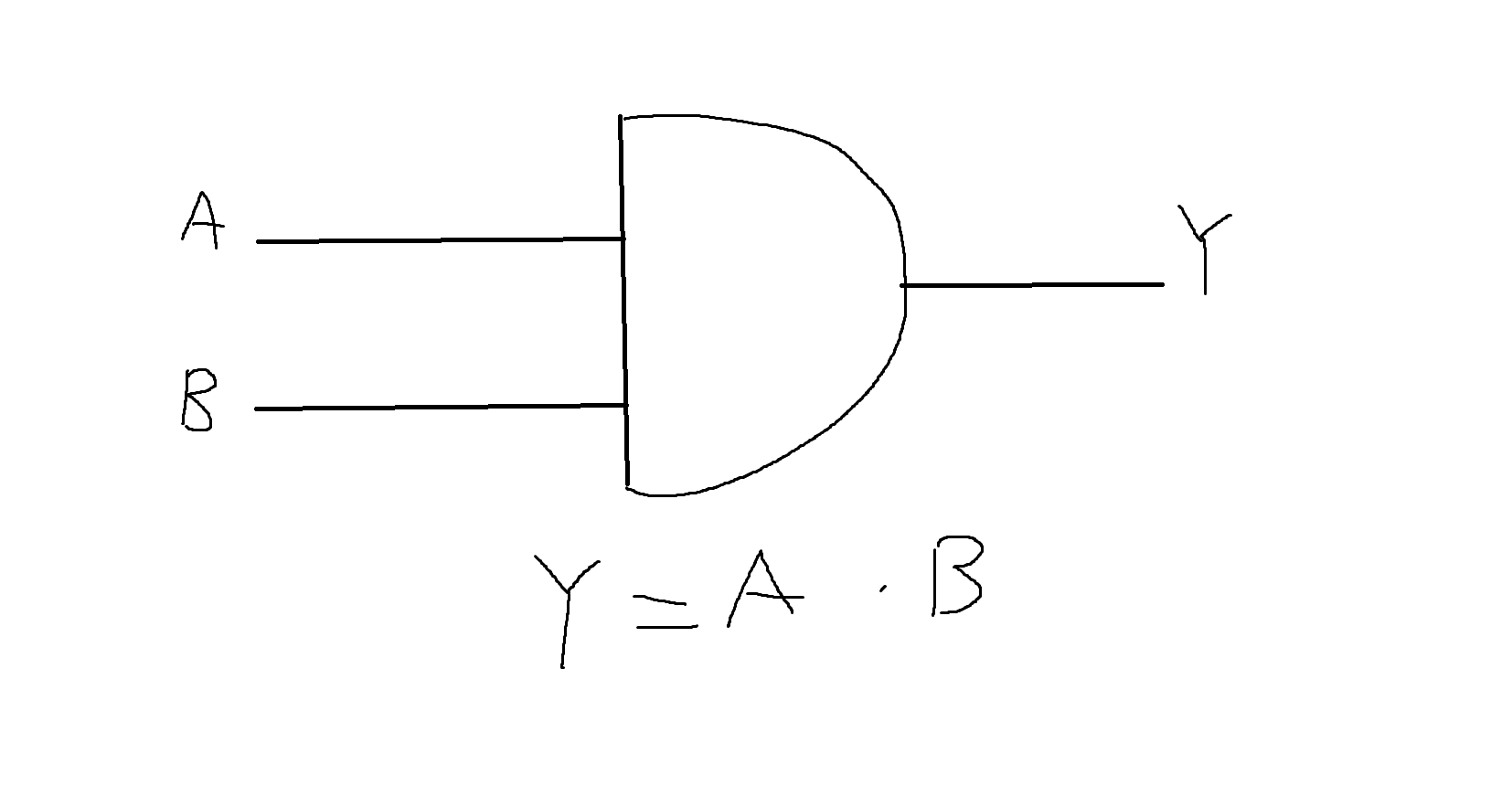
(2) 논리합회로 (OR Gate)
- 입력 A와 B중 적어도 하나가 1일 때 출력 Y가 1이 됨
- +로 표현
- OR Gate는 스위치가 병렬로 연결 -> 두 스위치 중 하나만 1이 되면 회로가 연결
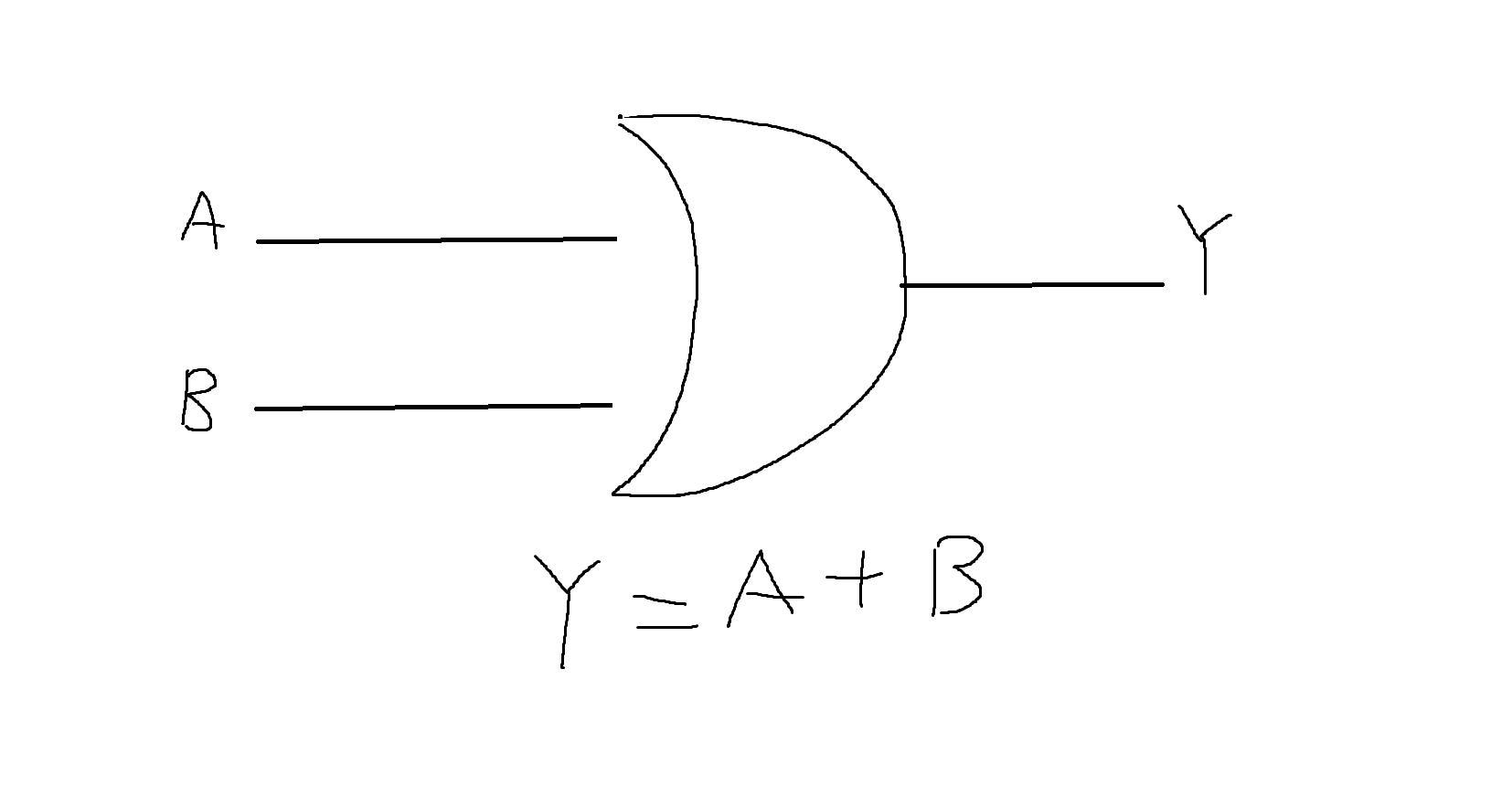
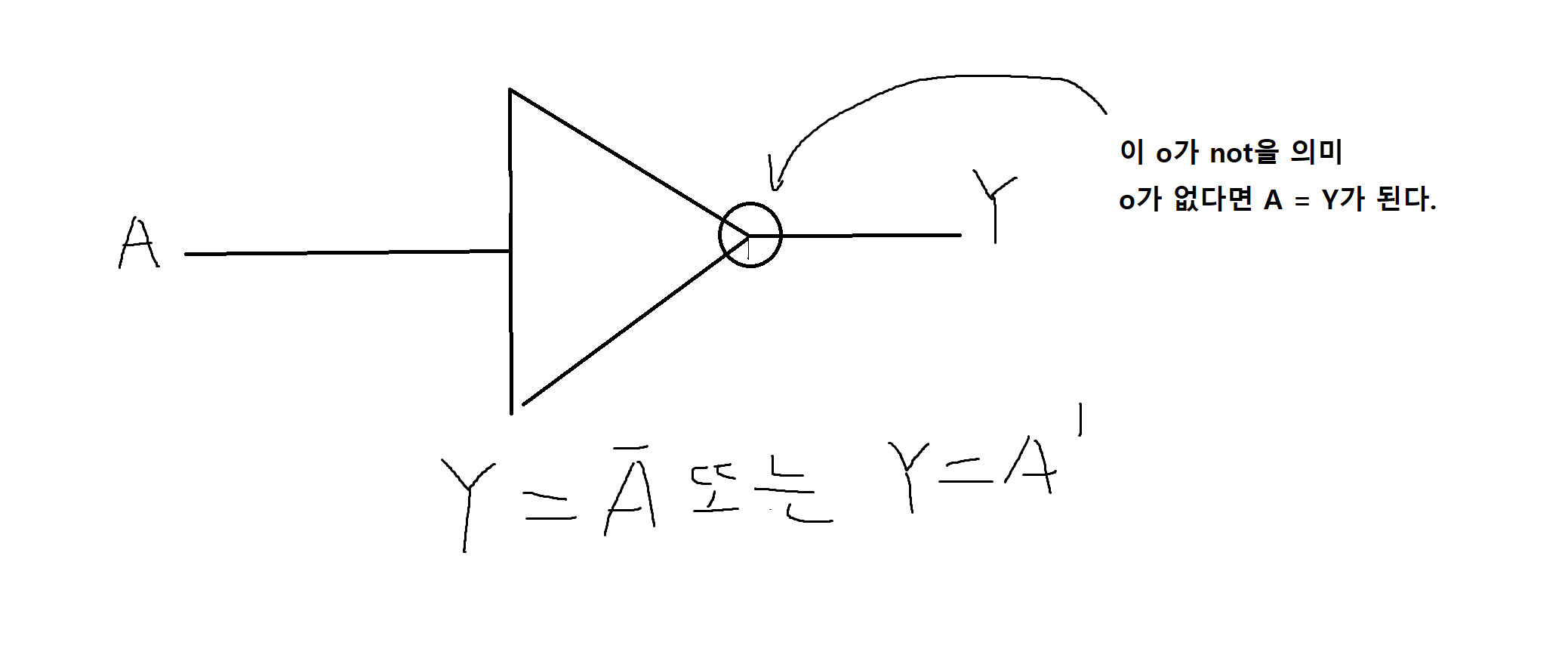
(3) 논리부정회로 (NOR gate)
입력 A = 1 -> 출력 Y = 0
입력 A = 0 -> 출력 Y = 1
- "'" 또는 '-'로 표현 됨
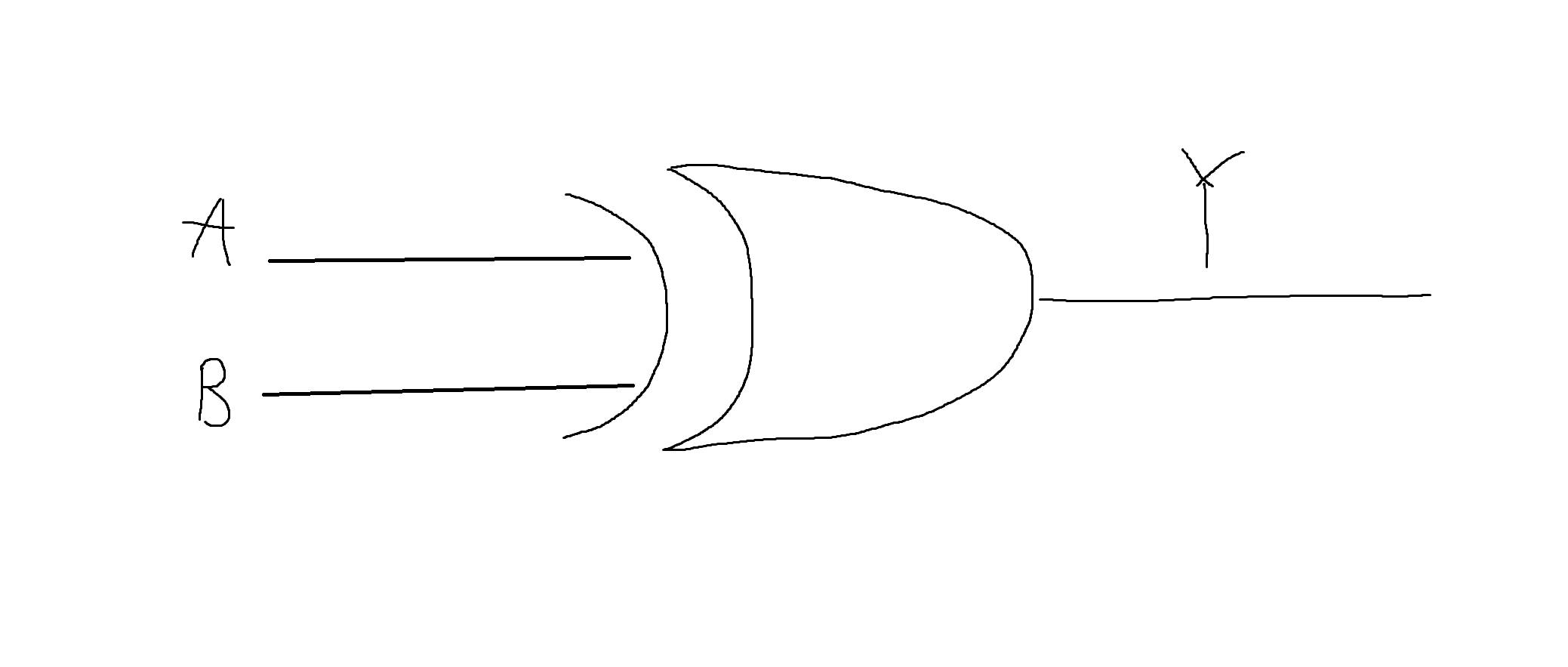
(4) 배타적 논리합 (XOR) (Exclusive OR gate)
| X | Y | XOR |
|---|---|---|
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| 1 | 1 | 0 |
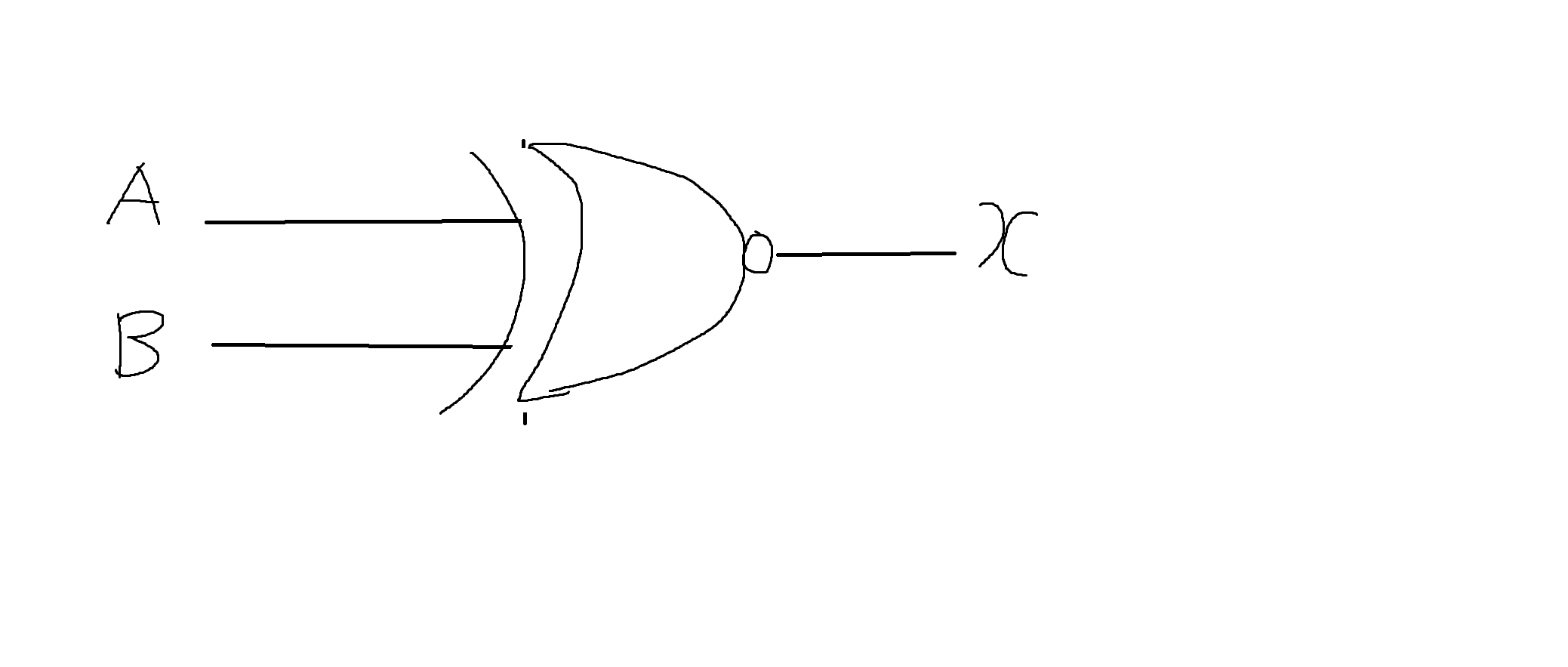
(5) NAND (Not And) -> (A∩B)'

| A | B | x |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
(6) NOR
| A | B | Y |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
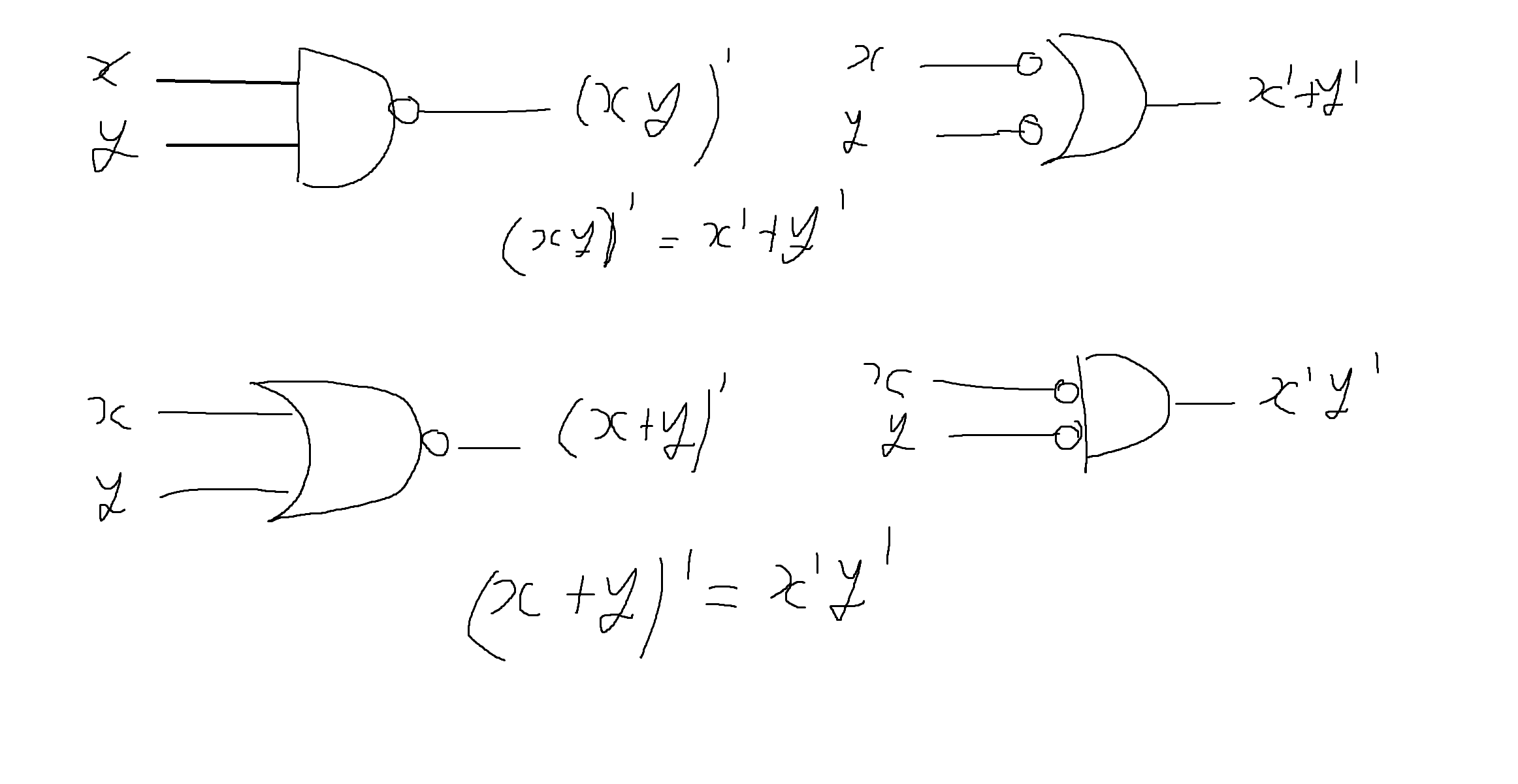
-
NAND 게이트와 NOR 게이트에 드모르간의 법칙을 적용하면 위와 같다.
-
AND, OR, NOT 세 가지로 모든 논리함수를 만들 수 있다. (논리 함수의 완전성)
예제 11-14. 다음 부울식을 논리 회로로 표현해보자.
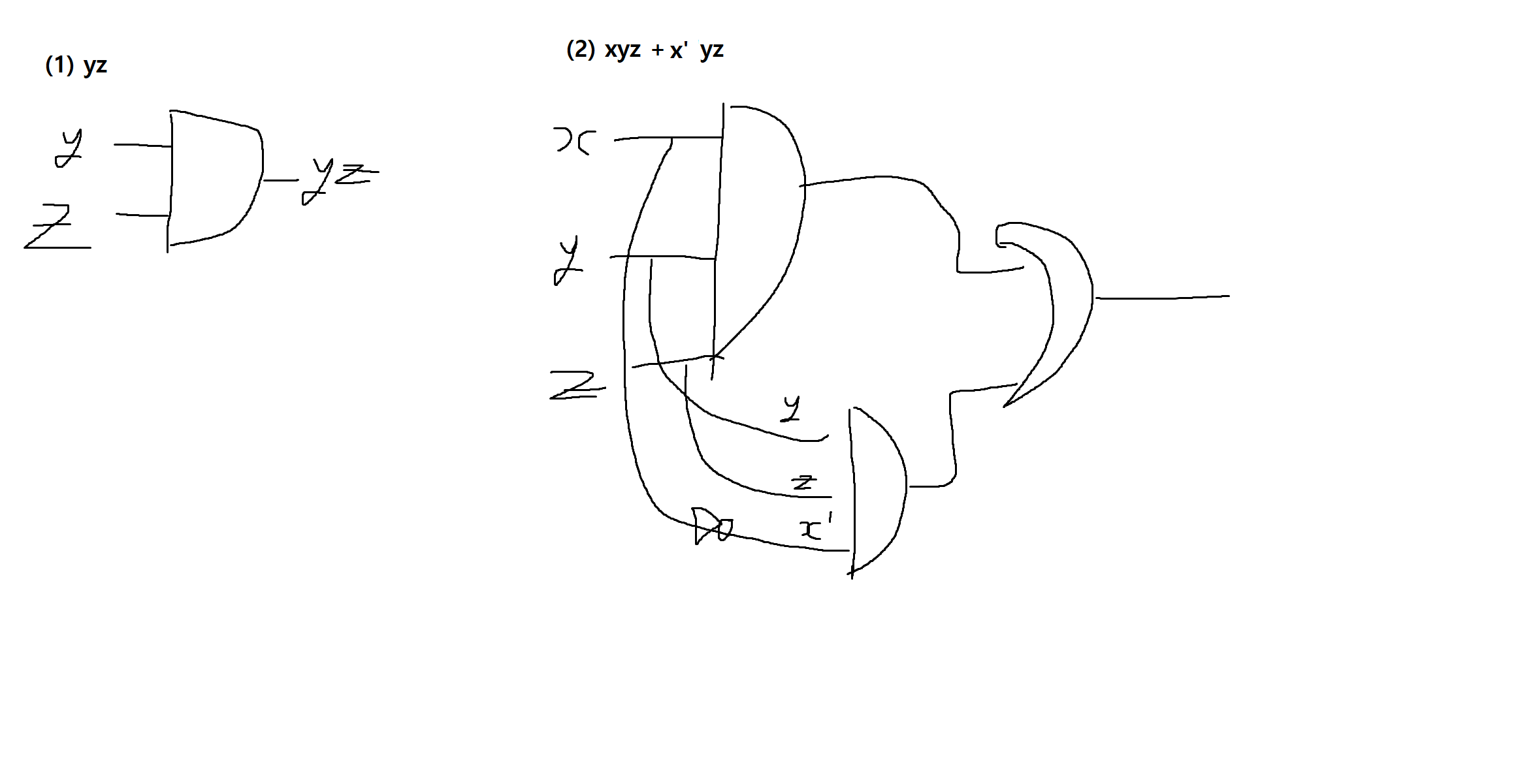
xyz + x'yz
= yz(x + x')
= yz
카노우맵으로 하면)
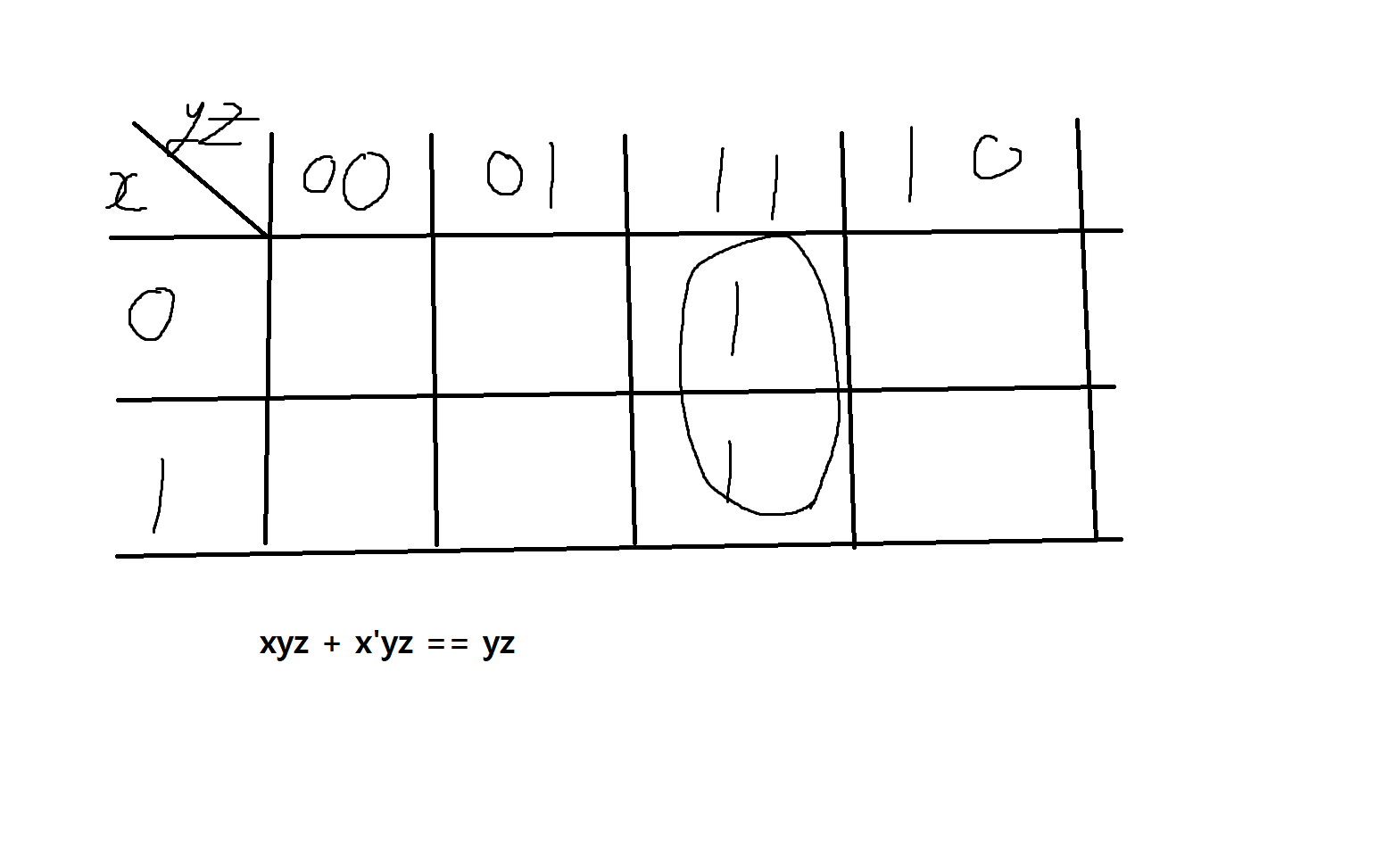
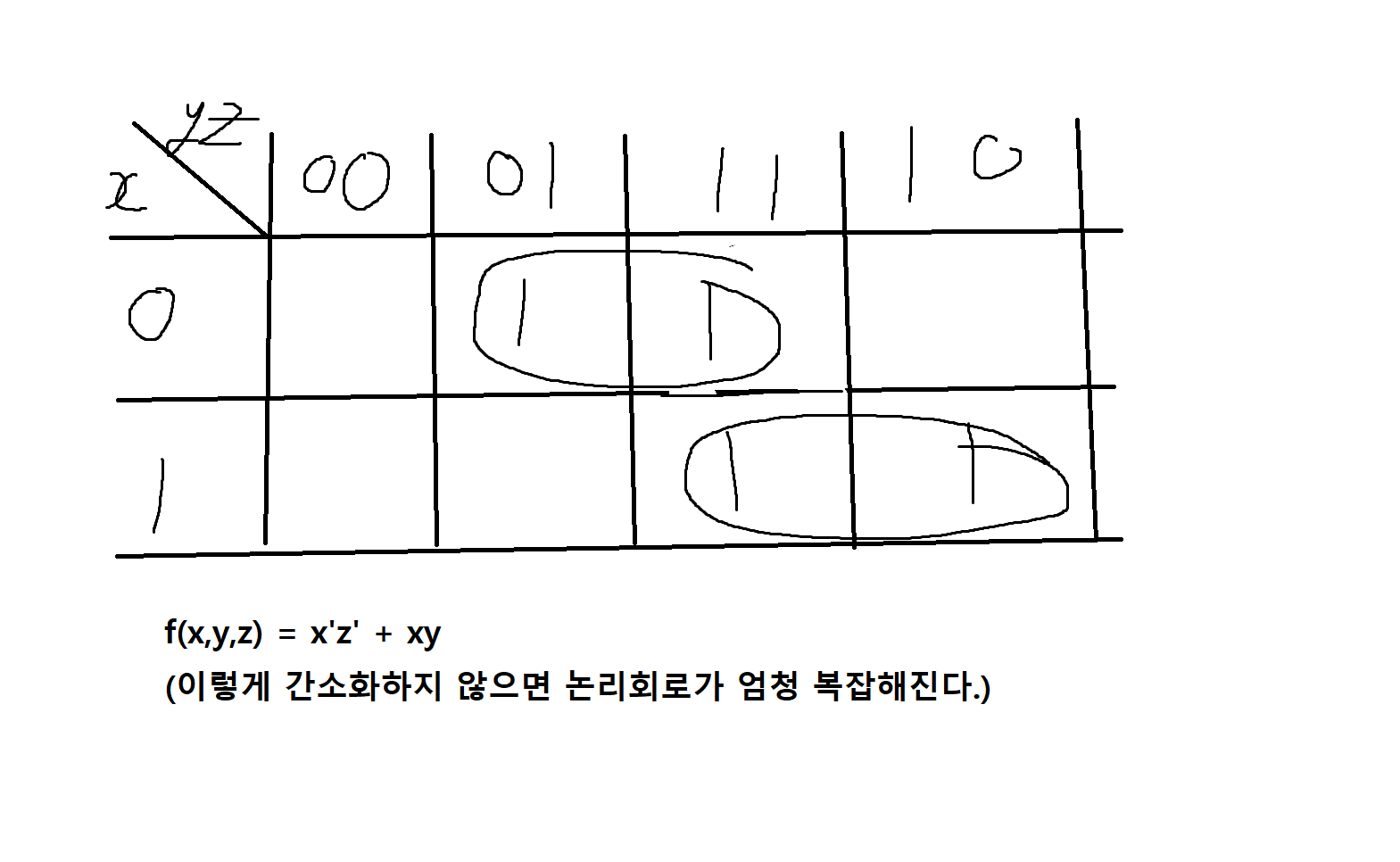
예제 11-15. 다음 부울함수를 간소화하고 간소화 된 함수의 논리회를 그려보자.
f(x,y,z) = x'y'z + x'yz + xyz + xyz'
-> 이걸 그대로 논리회로화 하는 건 힘듬 (8개의 gate 필요)
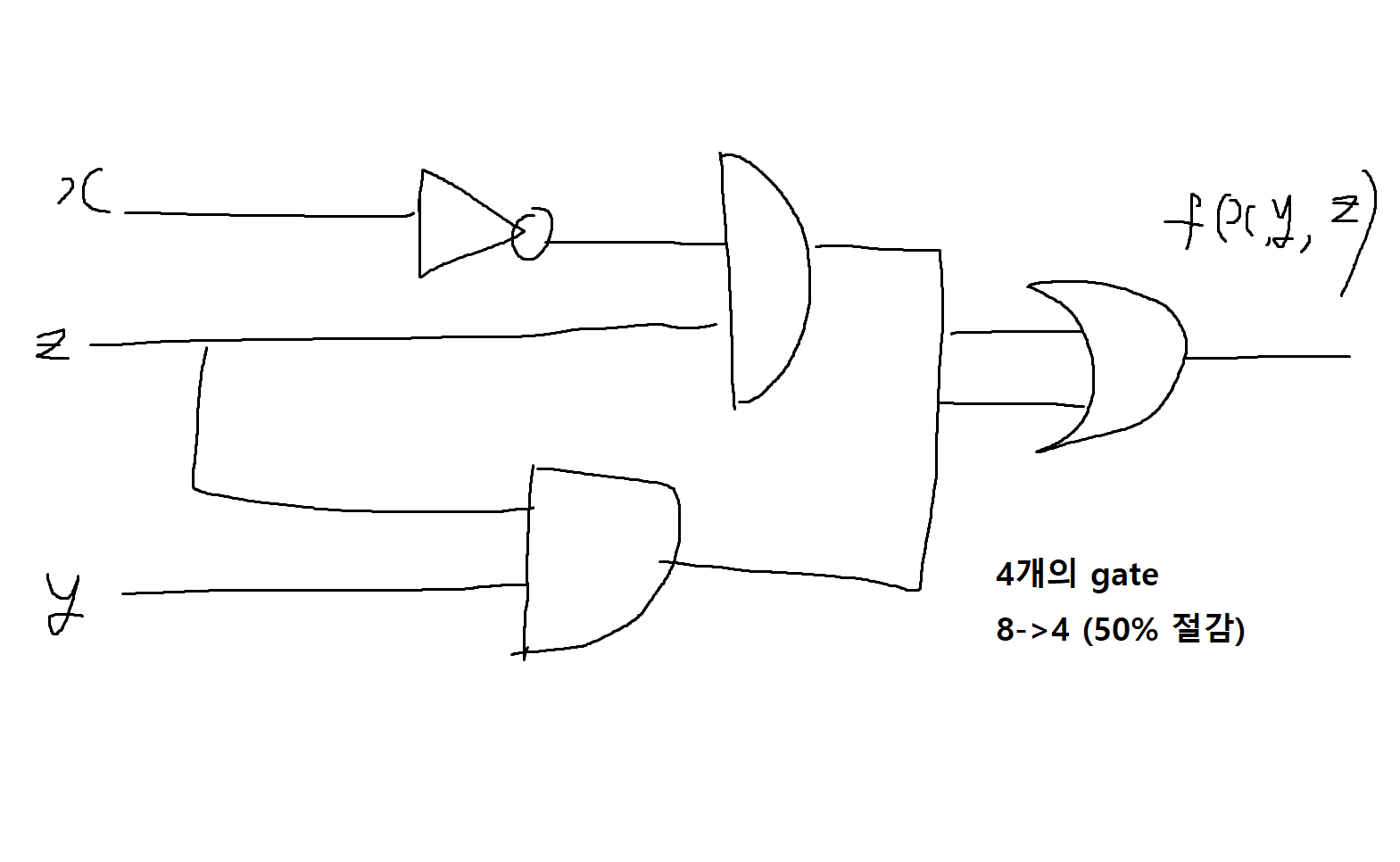
예제 11-16. 다음 논리회로에 해당하는 부울함수를 구해보자.
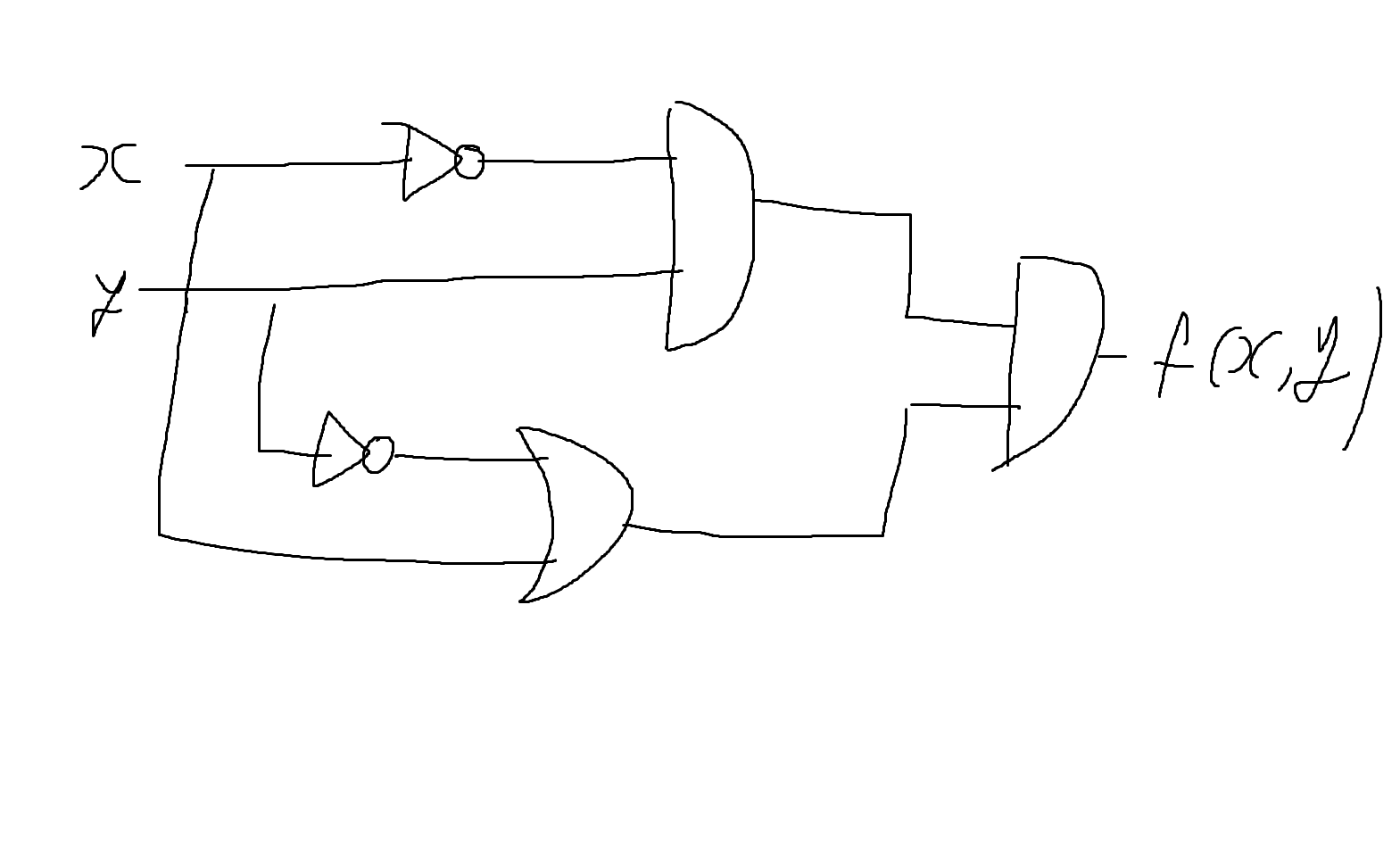
f(x,y) = x'y * (x+y')
= x'yx + x'yy'
= (xx')y + (yy')x' -> (xx'=0, yy'=0)
= 0
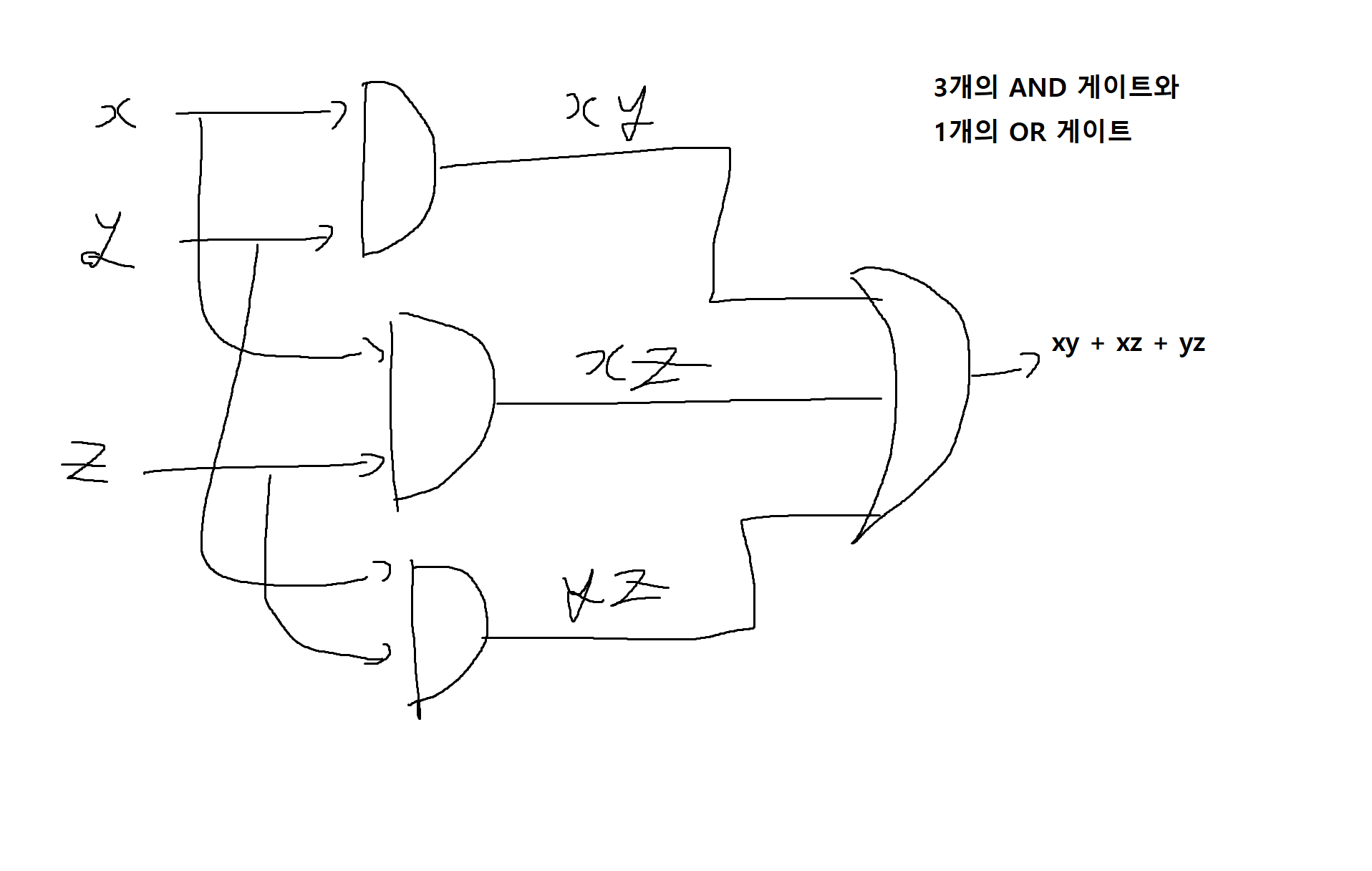
(2) 전자투표기
- 3명이 어떤 안건에 대해 '찬성', '반대'중 하나를 투표하고 2명 이상이 '찬성'할 때 안건이 통과. 이를 논리회로로 그리면 아래 그림과 같음
연습문제
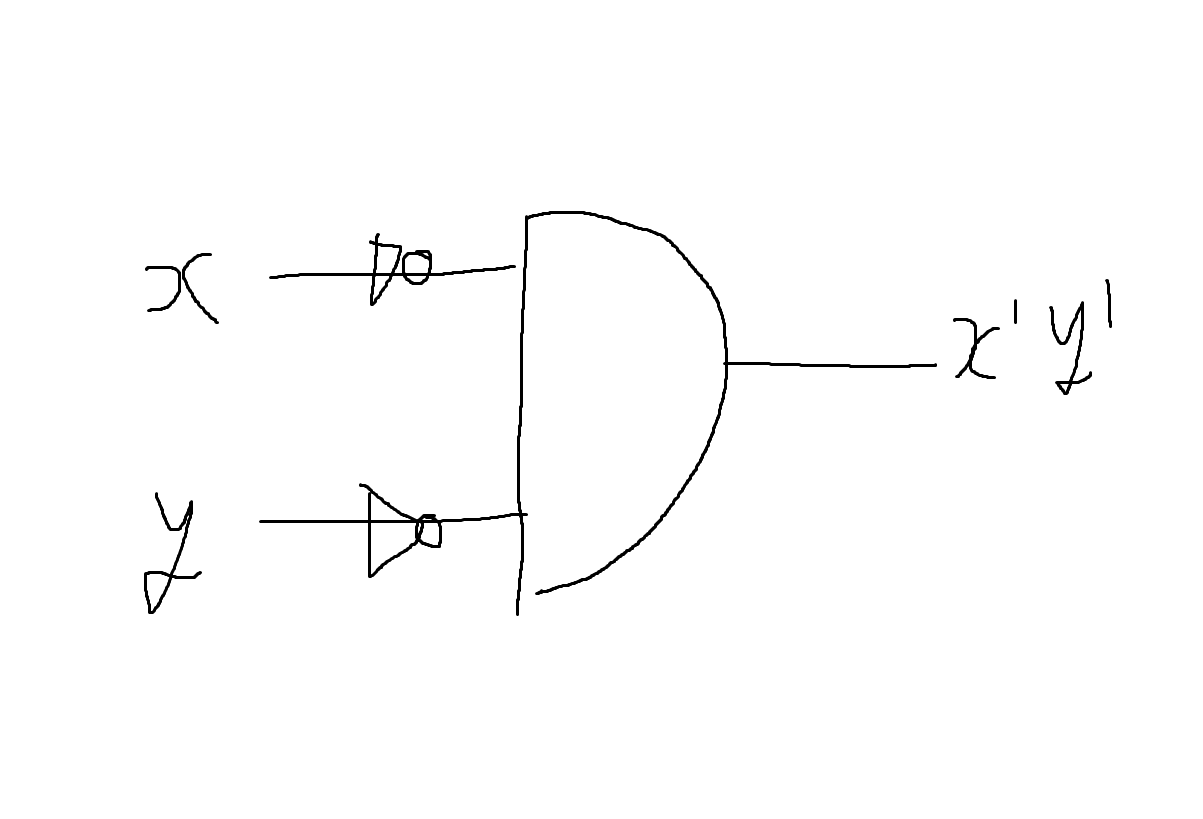
1) 다음 부울함수에 대한 논리회로를 그리시오.
(x'+y) y'
-> x'y' + y y' = x'y'
2) 다음 부울함수에 대한 논리회로를 그려라
(x+y) (x'+z')
= x x' + x z' + y x' + y z'
= x z' + y x' + y * z'
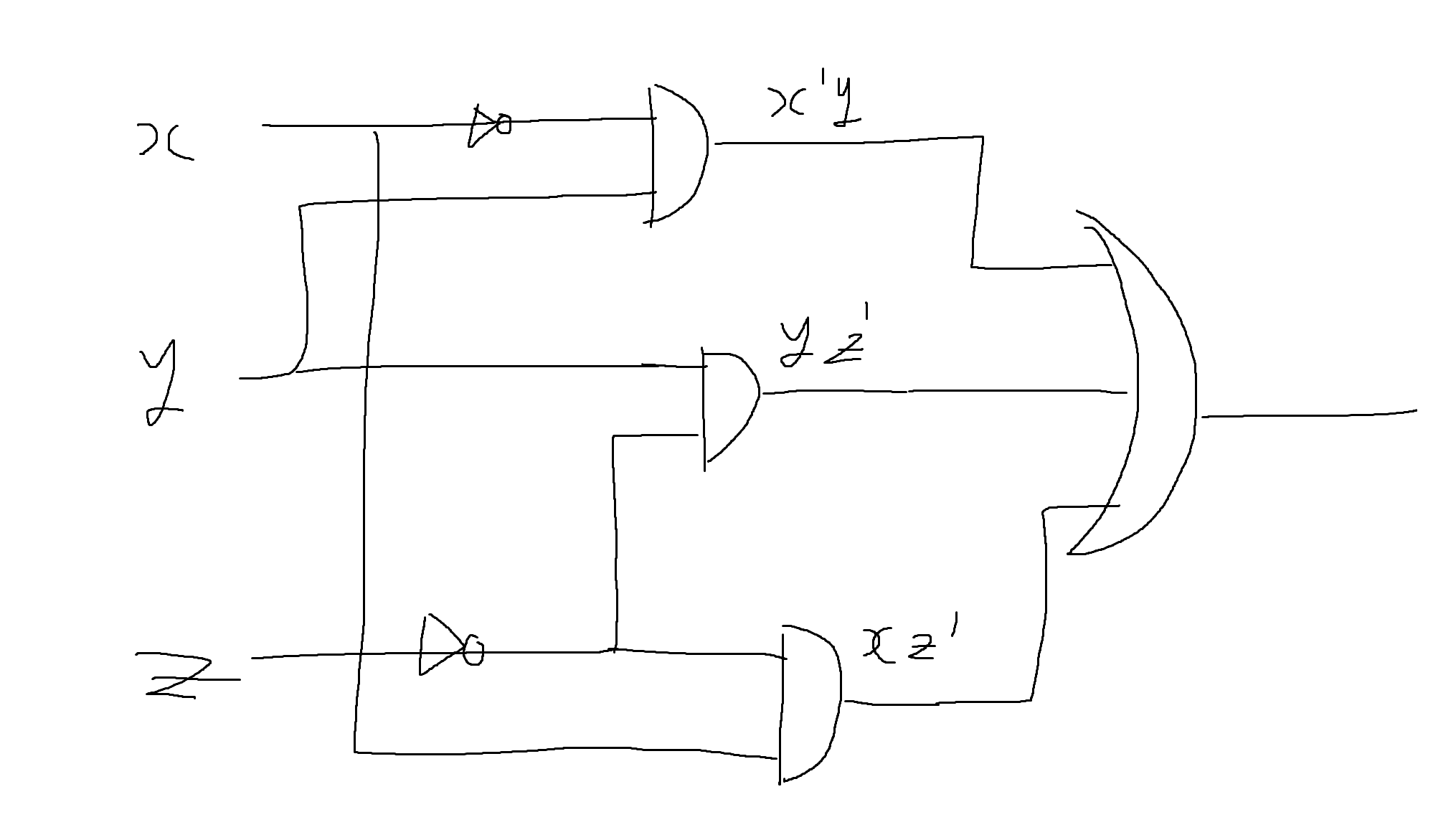
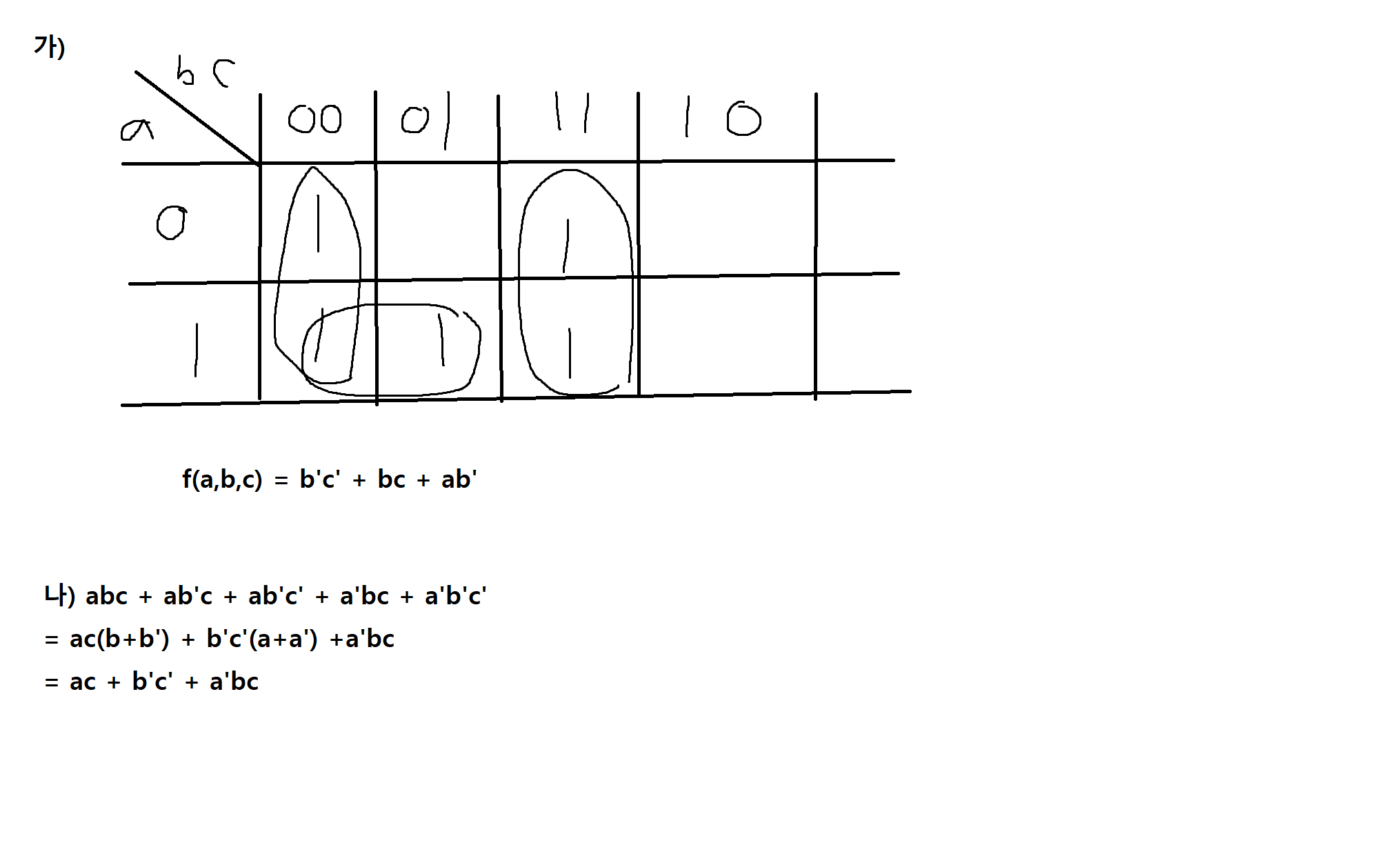
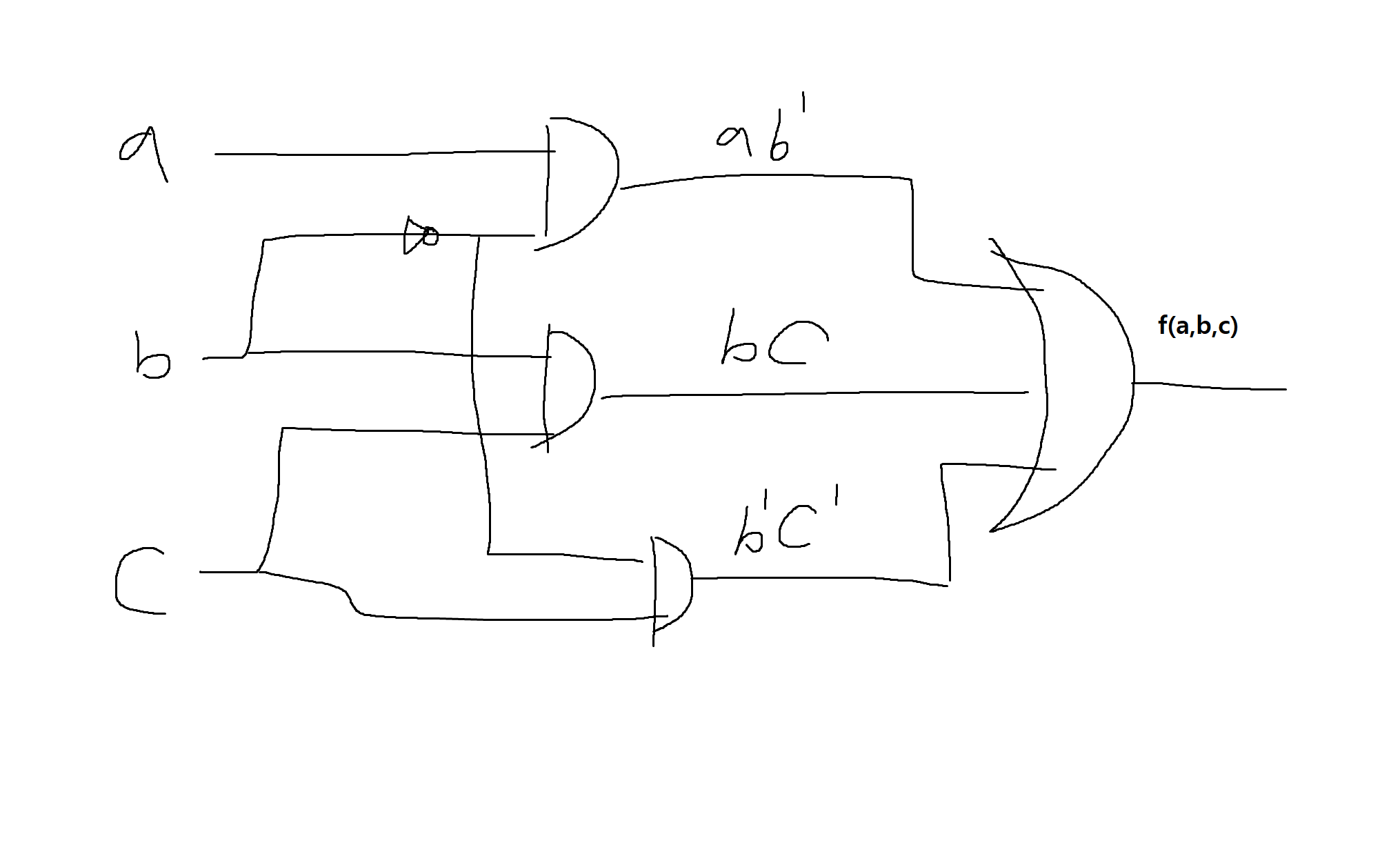
3) f(a,b,c) = abc + ab'c + ab'c' + a'bc + a'b'c'인 부울함수를
가) 카노우맵을 사용하여 간소화하시오.
나) 부울식의 기본법칙을 사용해 간소화 하시오
다) 간소화된 함수의 논리회로를 그리시오