(현실) 수학적 확률로
-
몬티홀 문제
-
확률지식을 요구 (전공과목을 배우는데 필요한)
-
수학적 공리에 근거한 확률론을 학습
-
베이즈 정리, 확률변수, 가우스 확류련수
확률론의 기본
- 집합론의 기본
집합 -> 대상들의 모임 (대상 = 원소 = 집합을 구성하는 대상)
a∈A (a는 A의 원소이다)
(집합은 대문자, 원소는 소문자로 표현)
벤 다이어그램
부분집합
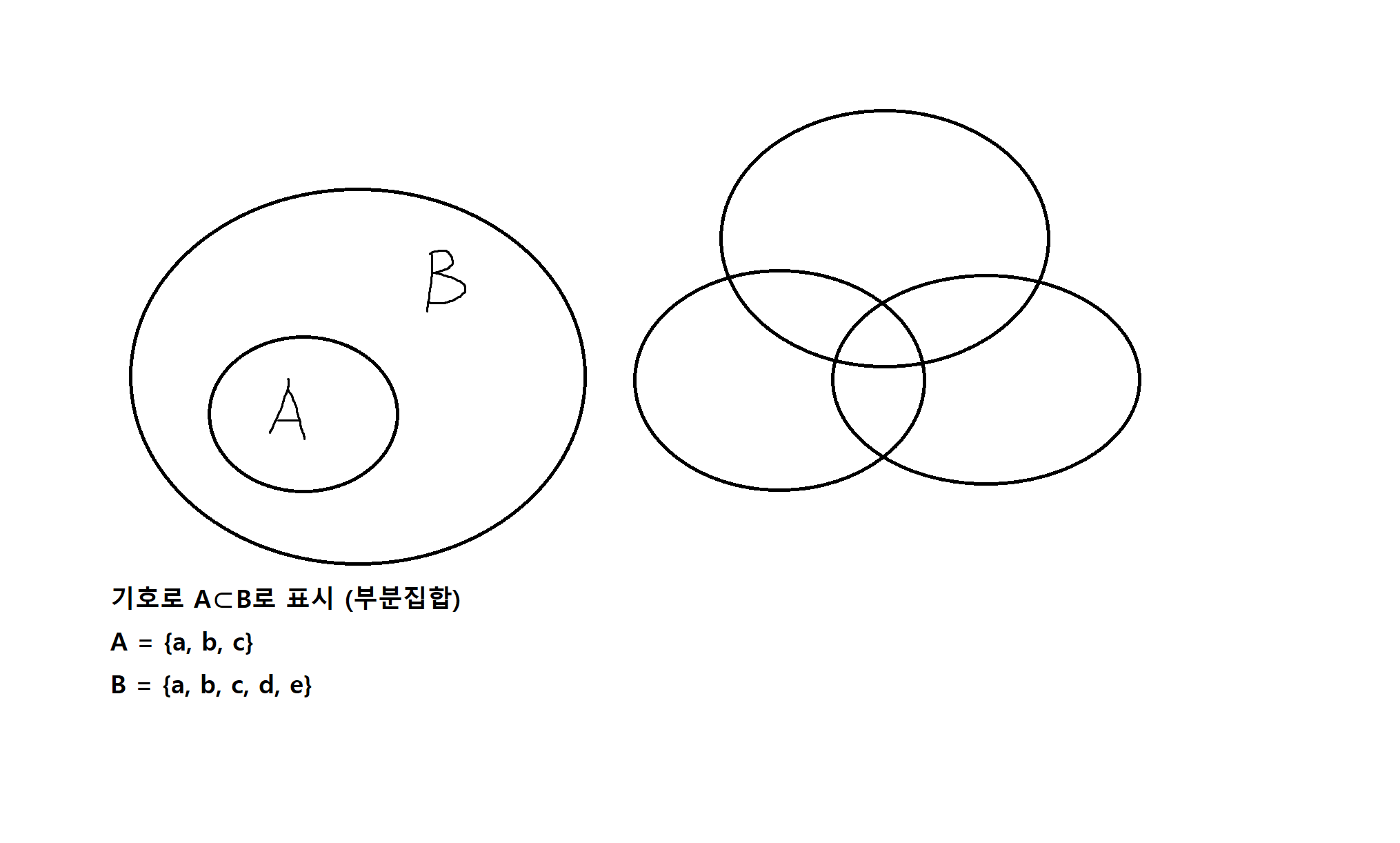
특수한 집합
- 전체 집합 U : 주어진 환경에서 관심있는 모든 대상들의 집합
- 공집합 ∅ : 아무 원소도 가지고 있지 않은 집합
- 카디날리티 |S| : 집합에 포함되있는 서로 다른 원소의 수
A = {a,b,c}
|A| = 3
-
원소개수 유/무한에 따라 유한/무한 집합으로 구분
-
합집합 A∪B
-
교집합 A∩B
-
서로소 -> A,B의 교집합이 공집합일 때, 두 집합은 서로소 관계
-
여집합 (A^c) -> A에 속하지 않는 모든 원소의 집합
-
차집합 A-B -> 공통적으로 겹치는 부분만 빼준다
-
멱집합 : 집합 S에 대하여 S의 모든 부분집합을 원소로 가지는 집합
P(S) 혹은 2^s로 표기
P(S) = {A|A⊂S}, |P(S)| = 2^|s|
A = {1,3}
P(A) = {∅, {1}, {3}, {1,3}}
S = 2^n = 2² = 4
P(S) = 2^|s| = 2⁴ = 16개
합집합 sum i=1 to n Ai = A₁∪ A₂∪ A₃...∪An
교집합 A₁∩ A₂∩ A₃...∩An
곱집합 A * B : x∈A이고 y∈B인 모든 순서쌍 (x,y)의 집합
A = {1, 3} (1차원)
B = {2, 4} (1차원)
A * B
{(1, 2), (1,4)
(3,2), (3,4)}
조건제시법 A * B = {(x,y)|x∈A, y∈B}
순서쌍 (a, c) != (c, a)
예제 2-2.
S = {1,2,3,4}, T = {2,4}, {(x,y)|(x,y) ∈ S * T, x < y}
x < y조건 충족
-> (1,2), (1,4), (2,4), (3,4)
정수 Z, 자연수 N 유리수 Q, 실수 R
예제 2-3.
1) A = R R = R²
2) B = Z Z
3) C = N * N의 의미
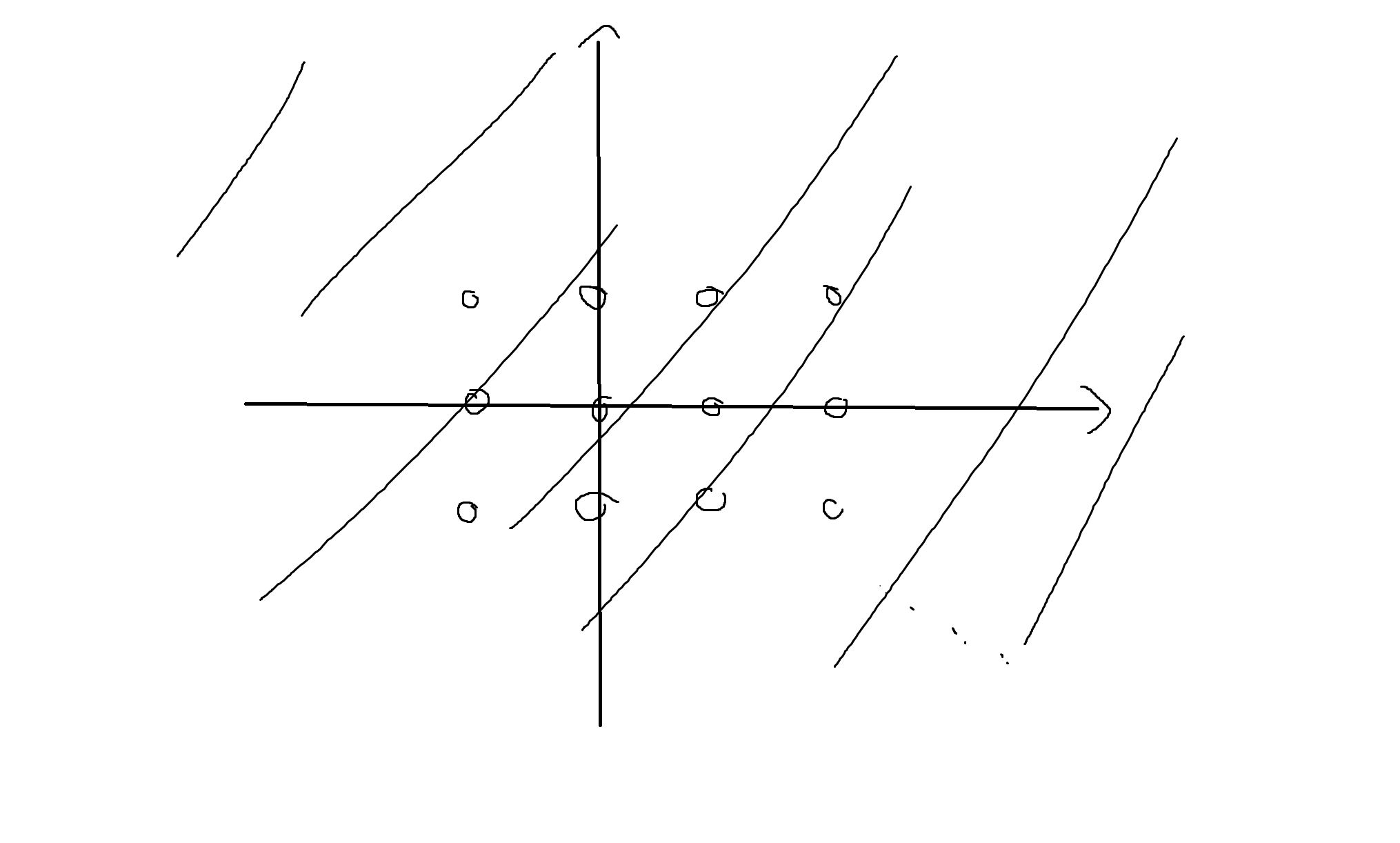
1) 실수인 순서쌍의 모음 (전체 범위)
2) 1) 중에서 정수점들의 모음
3) 2) 중에서 자연수 점들의 모음
-
교환법칙
A∪B = B∪A 그리고 A∩B = B∩A
-> A-B != B-A -
결합법칙
A∪(B∪C) = (A∪B)∪C 그리고 A∩(B∩C) = (A∩B)∩C -
분배법칙 (중요)
A∪(B∩C) = (A∪B)∩(A∪C)
A∩(B∩C) = (A∩B)∪(A∩C) -
드모르간 법칙 (중요)
(A∪B)^c = A^c ∩ B^c 그리고 (A∩B)^c = A^c ∪ B^c
예제 2-1. U = (x|1<=x<=10, x∈N}, A={1,3,9}, B={1,2,3,4,5,6,7}
(1) A∩B
{1,3}
(2) A와 서로소 관계인 어떤 집합 C
-> 1,3,9를 제외한 원소를 가진 집합
(3) B^c ∩ A
= A-B = {9}
(4) A^c ∩ B^c
= (A∪B)^c = {8, 10}
(5) P(A)
2^|s| = 2^3 = 8개
P(A) = {∅. {1}, {3}, {9}, {1,3}, {1,9}, {3,9}, {1,3,9}}
∅ ∈ P(A) (공집합은 P(A)의 원소이다)
∅ ⊂ P(A) (공집합은 P(A)의 부분집합이다)
확률모델의 필요성
-
모델링 : 실제하는 현실을 다양한 방식으로 분석, 예측하는 방법
결정모델 vs 확률모델
모델링 방법에 따라 다양한 수학이 활용됨 -
결정모델 -> 실험 조건이 주어졌을 때, 정확한 결과가 예측가능한 시스템으로 모델링
예) V = I * R -
확률모델 -> 실험조건(입력값)이 주어지더라도 정확한 결과를 예측할 수 없는 시스템을 모델링
예) 주사위 던지기. 1/6 확률로 3
Q. 확률?
-
어떤 일이 일어날 가능성
-
불확실성을 측정하는 척도
-
고전적 접근법 -> 그것이 일어날 수 있는 경우의 수 대 가능한 모든 경우의 수의 비, 모든 사건이 동일하게
-
상대도수 : 어떤 사건이 일어나는 빈도수
-
공리적 접근법 - 수학적 확장을 위한 확률의 정의
확률실험 : 실험이 같은 조건에서 반복될 때 그 결과가 예측할 수 없는 방식으로 변하는 실험
같은 절차로 구성된 실험도 관측하고자 하는 값에 따라 결과가 다르다.
예제 2-4.
(1) 실험 E₁: 동전을 3번 던져 앞면과 뒷면의 순서를 기록
-> HHH, HHT, HTT, TTT
(2) 실험 E₂: 동전을 3번 던져 앞면이 나올 횟수를 기록
-> 3, 2, 1, 0
표본 공간(Sample space) -> 나올 수 있는 모든 가능한 결과들의 집합
예제 2-5. 예제 2-4의 각 실험의 표본공간을 구하시오.
E₁-> S = {HHH, HHT, HTH, ... HHH}, 2³ = 8개
E₂ = S = {0, 1, 2, 3}
이산표본공간 : 불연속 표본점 (어느 한 지점에서의 확률값 P(x=a)을 뜻함)
예제 2-6. 동전의 앞면이 나올 때까지 던진 횟수
S = {1,2,3,4,5...} -> |S| = ∞
(크기가 무한대가 될 수도 있다)
연속표본공간 : 연속 표본점 (연속형 데이터를 담고 있는 표본공간)
예제 2-7. 0과 1사이에서 임의로 선택한 실수값
S = {x|x ∈ [0,1], x ∈ R}
-> 무한대에 해당함
확률적 사건 (event)
-
기본사건 : 1개의 결과로 이루어진 사건 (이산표본공간)
-
특정사건 A는 표본공간 S의 부분집합. A⊂S
-
사건 자체를 집합으로 간주하고 사건 사이의 집합연산이 가능
-
확실한 사건 -> 항상 발생 (확률 1), A = S
-
공사건 -> 절대 발생하지 않음, A = ∅
-
사건클래스 F -> 표본공간 S에서 발생가능한 사건의 집합 (Power Set)
초기확률 할당 -> 이산표본공간의 경우 {a₁, a₂, a₃...}
-
일반적으로 같은 빈도의 결과를 가정
-
표본공간 S의 기본 사건은 서로소 관계 (서로 배반적)
-
기본사건의 확률 1/n
-
k의 결과로 이루어진 사건 B
P[B] = k/n
예제 2-10. 동전을 3번 던진다고 가정. 앞면과 뒷면의 순서를 관찰한다면, 앞면이 2번 나올 확률은? (단, 동전의 앞면과 뒷면이 나올 확률은 동일)
S = {HHH, ... TTT} -> 8개
A = {HHT, HTH, THH}
P[A] = 3/8
초기확률할당 : 연속표본공간의 경우
- 사건이 한 점일 경우 : 결과가 특정값을 갖는 확률은 0
P[A] = 0
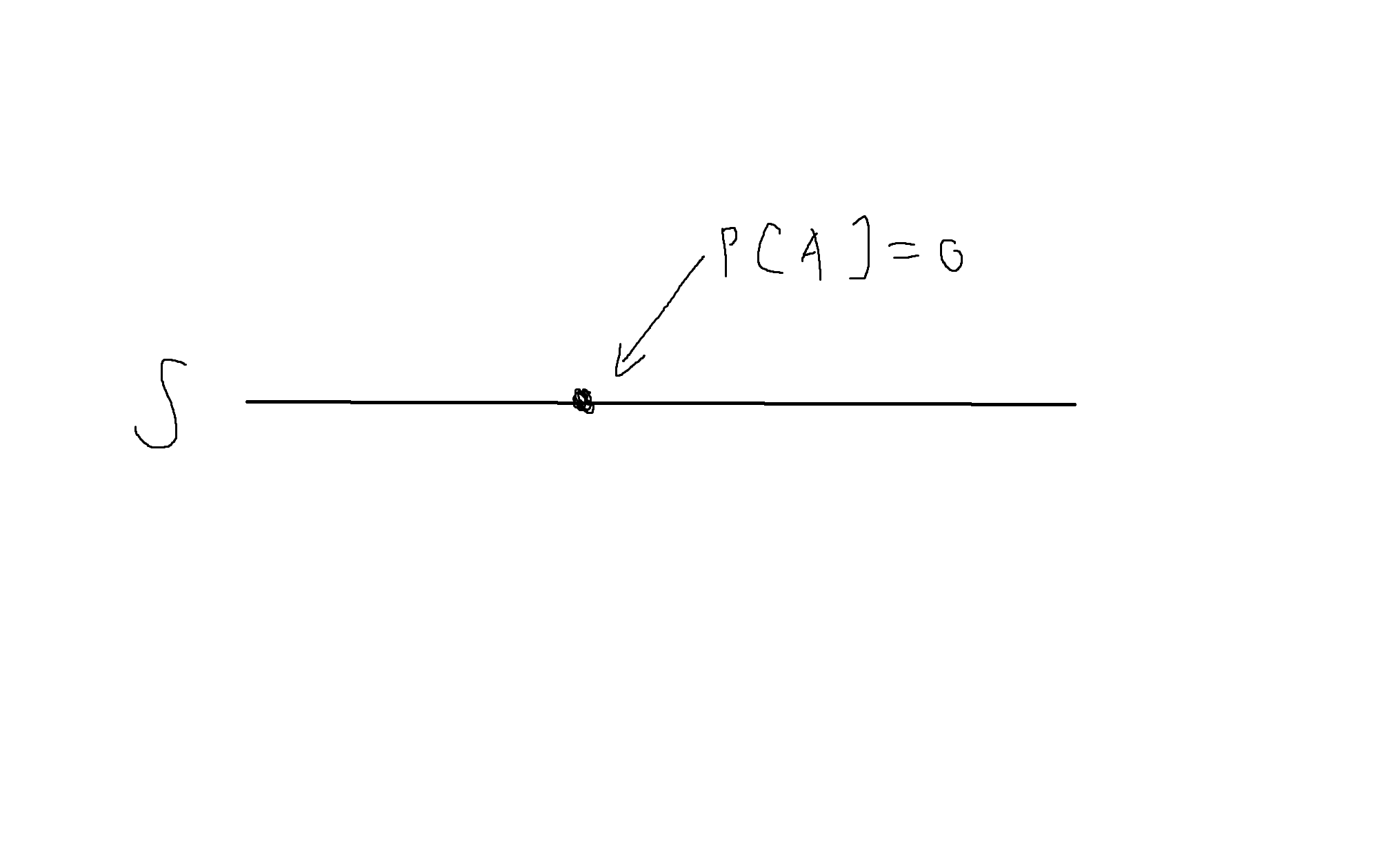
전체 집합 S에 무한히 많은 실수가 있으니 1/∞이니 0이 됨
- 사건이 구간일 경우 : 해당 사건이 차지하는 구간의 비율 (균등분포가정)
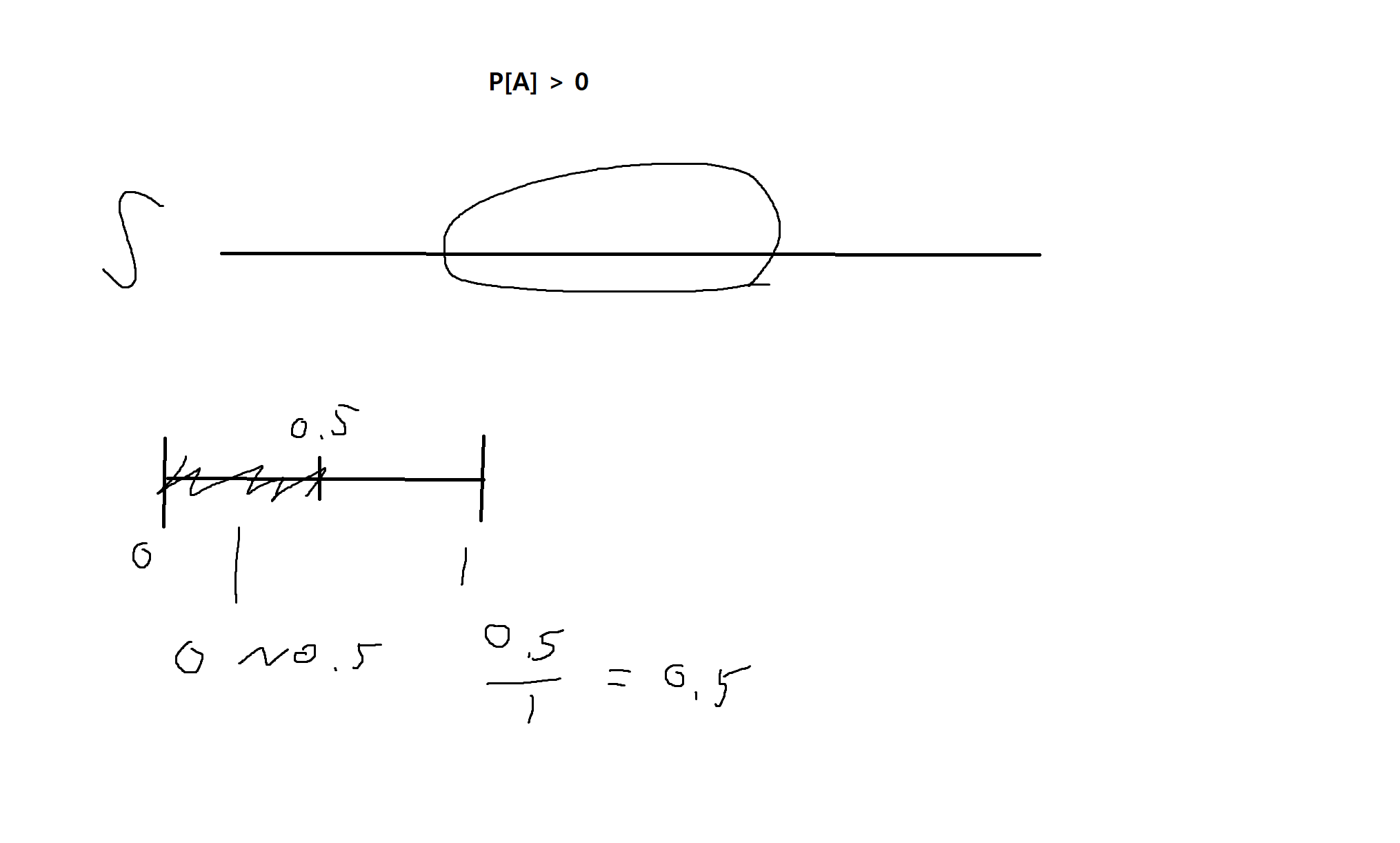
예제 2-8. 동전을 2번 던져서 나온 횟수를 기록할 때, 다음 사건의 의미
(1) 앞면이 나온 횟수가 1 또는 2
A = {1, 2}
{(H,T), (T,H), (H,H)}
P(A) = 3/4
확률의 공리 -> 확률법칙이 만족해야 하는 특성
- 0 <= P[A]
- P[S] = 1
- A∩B = ∅이면 P[A∪B] = P[A] + P[B]
예제 2-9.
(1) P[A^c] = 1 - P[A]
(2) P[A∪B} = P[A] + P[B] - P[A∩B]
(3) A⊂B이면 P[A] <= P[B]
예제 2-11. 0과 1사이에서 임의로 두 수 x,y,를 뽑는 실험을 생각했을 때, 다음 사건의 확률을 구하시오.
(1) A = {A > 0.5}

(2) B = {x²+y²<1}

-
조건부 확률 : P[A|B] : 사건 B가 발생했을 때 사건 A의 발생확률
P[A|B] = P[A∩B] / P[B] -
사건 B가 발생했다는 것은 실험의 결과가 집합 B안에 포함되는 것을 의미
(표본공간이 B로 축소되는 것으로 간주)
예제 2-12.
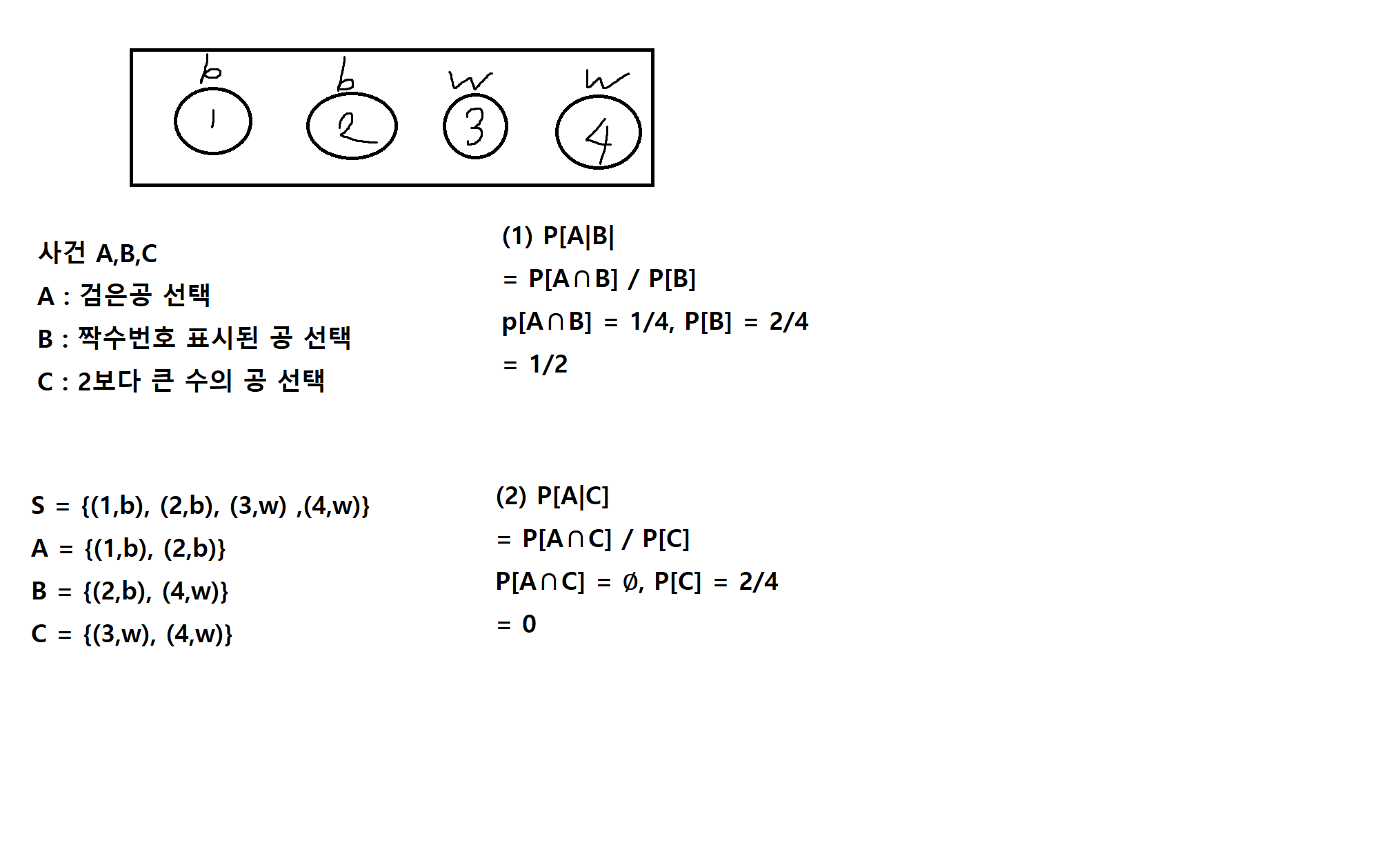
분할 (Partition) : 표본공간 S의 분할 π는 다음의 세 조건을 만족
(1) i = 1,...,k에 대해서 Bi ⊂ S이고 Ai != ∅
(2) S = sum i=1 to k Bi (집합을 다 모으면 S가 된다)
(3) i != j 이면 Bi ∩ Bj = ∅ (서로소관계)
(각 사건들이 서로소 관계) == 교집합이 없다
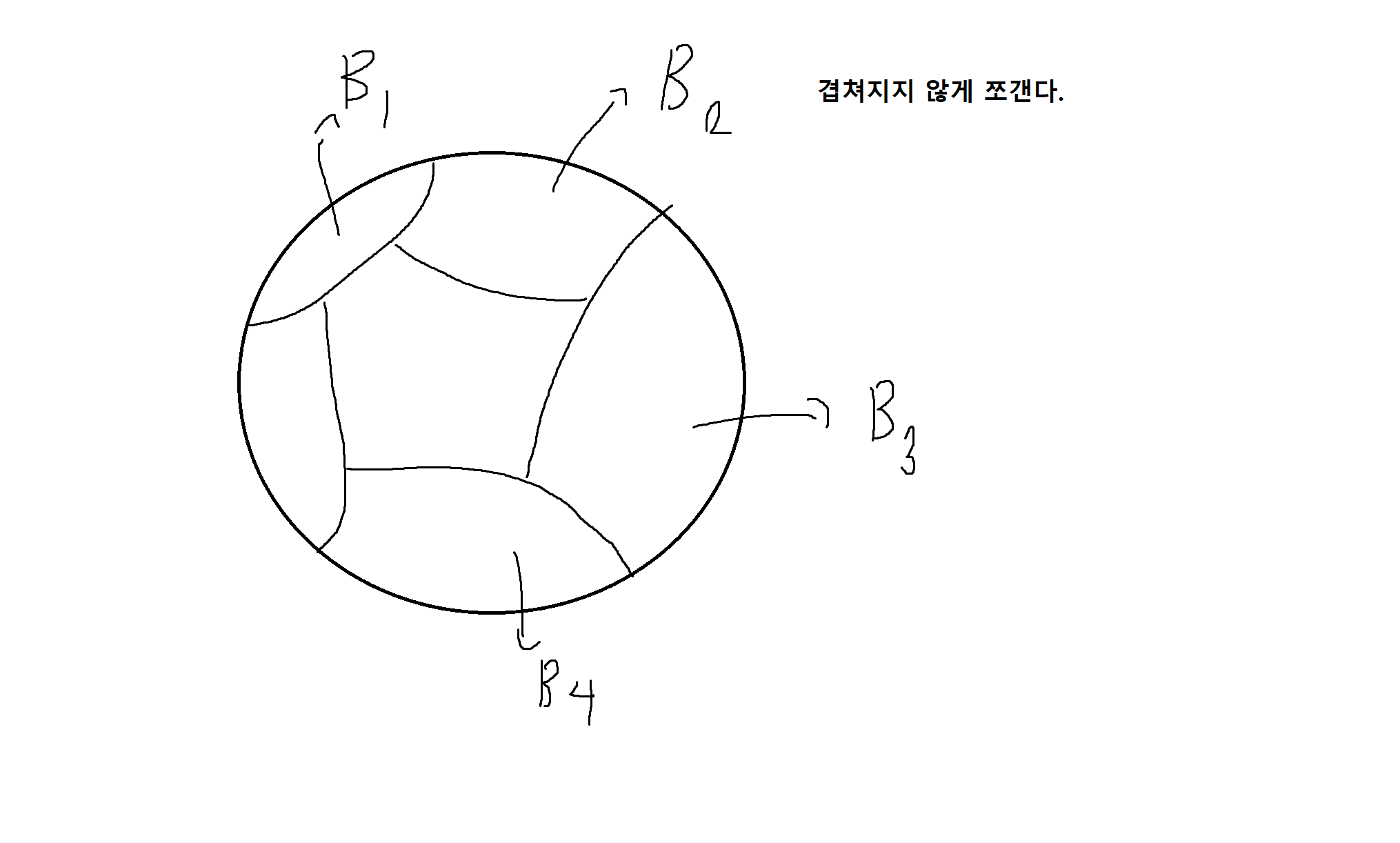
베이즈정리 (중요)

예제 2-13. 이진통신 시스템에서 데이터 0 또는 데이터 1을 보낼 확률을 각각 0.5이고, 데이터를 보냈을 때 정상적으로 수신되지 않을 확률은 0.1이다. 이때, 데이터 1을 수신했을 때, 실제로 0을 보냈을 확률을 구하여라.
문제에서 주어진 것
P[T0] = P[T1] = 0.5
P[R0 | T1] = P[R1 | T0] = 0.1
구하려는 것 -> P[T0 | R1]
P[T0 | R1] = P[T0 ∩ R1] / P[R1]
1)
P[T0 ∩ R1] = P[R1 ∩ T0]
= P[R1 | T0] P[T0]
= 0.1 0.5 = 0.05
2) 모든 분할에서 R1의 값
P[R1] = P[R1 | T0] P[T0] + P[R1 | T1] P[T1]
= 0.1 0.5 + 0.9 0.5
= 0.5
∴ 0.05 / 0.5 = 0.1
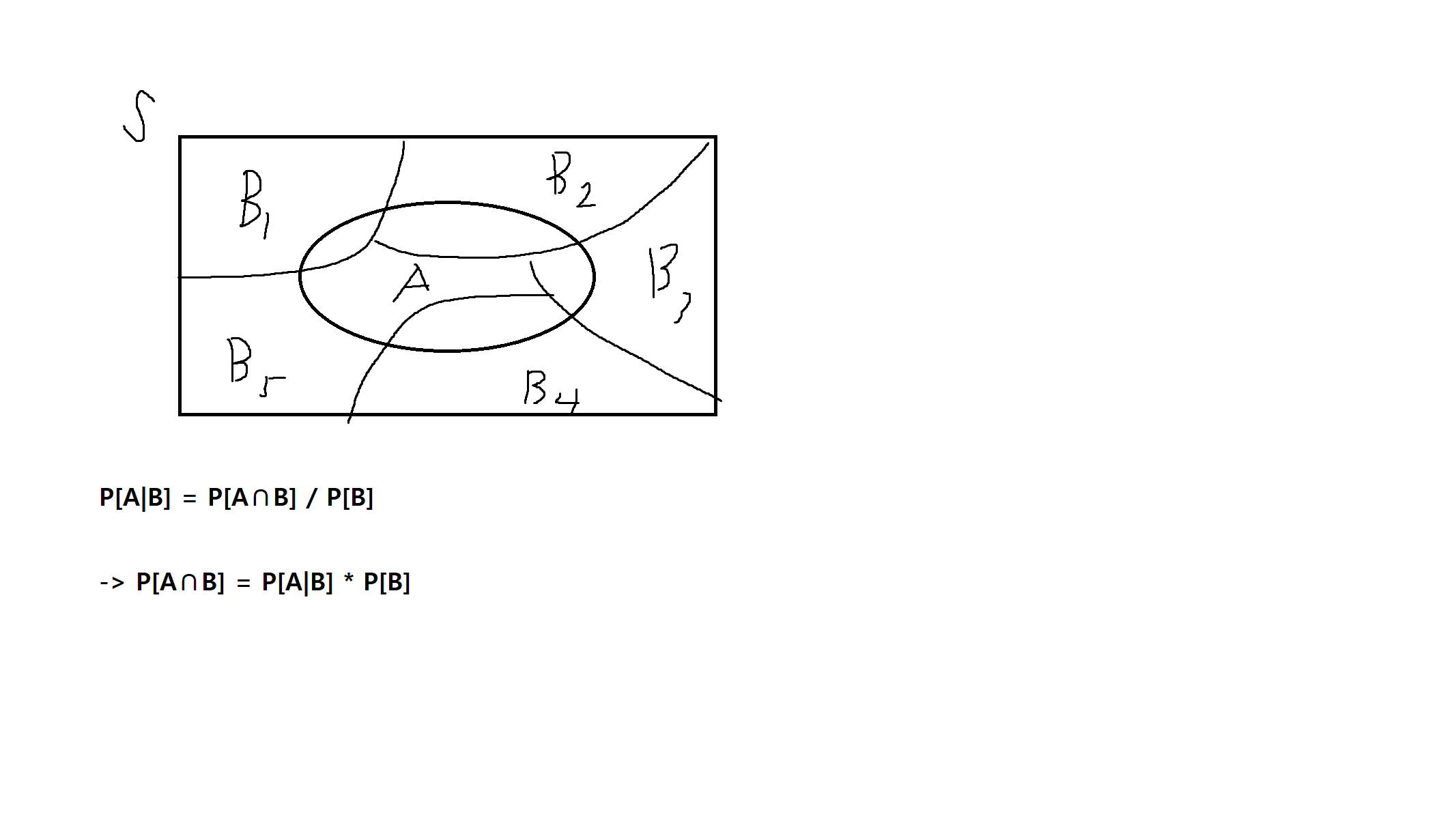
전체 확률에 대한 정리
- 사건 B₁, B₂..., Bn가 표본공간 S의 분할일 때,
A = A∩S = A ∩ (B₁∪ B₂∪...∪ Bn) = (A ∩ B₁) ∪ (A ∩ B₂) ∪...∪ (A∩Bn)
-> P[A] = P[A∩B₁] + P[A∩B₂] + ... + P[A∩Bn]
∴ P[A] = P[A|B₁] P[B₁] + P[A|B₂] P[B₂] + ... + P[A|Bn] * P[Bn]

예제 2-14. 데이터 0을 선택해서 보내는 확률이 1/3이고 데이터 1을 선택해서 보내는 확률이 2/3인 이진통신시스템에서 데이터를 보냈을 때, 정상적으로 수신되지 않은 확률은 0.1이다. 이때, 데이터 0을 수신했을 때, 실제로 1을 보냈을 확률을 구하여라.
문제에서 주어진 것
P[T0] = 1/3
P[T1] = 2/3
P[R1 | T0] = P[R0 | T1] = 0.1
구하려는 것
P[T1 | R0]
= P[T1 ∩ R0] / P[R0]
1)
P[T1 ∩ R0] = P[R0 ∩ T1]
= P[R0 | T1] P[T1]
= 0.1 2/3 = 2/30
2)
P[R0]
= P[R0 | T1] * P[T1] + P[R0 | T0] P[T0]
= (0.1 * 2/3) + (0.9 * 1/3)
= 2/30 + 9/30 = 11/30
∴ (2/30) / (11/30) = 2/11
