관계 (1)
(관계와 이항관계, 관계의 표현)
- 관계란 객체들간의 연관성을 표현하는 구조
관계의 예
- 집합 A와 집합 B가 있을때 A가 B의 부분집합일 경우 관계가 있음
- 공학과 수학에서 관계는 원소들간의 순서(order)를 고려
정의 5-1. 두 집합 A,B에 대해 A로부터 B로의 이항관계인 R은 두 집합의 곱집합 A B의 부분집합이다. A B의 원소인 순서쌍(a,b)가 주어졌을때 (a,b)∈R과 aRb는 동치이다.
aRb -> 관계있다.
aKb -> 관계없다.
- 이항(binary)이라는 용어는 2개의 집합 사이의 관계를 의미
- 2개이상 원소관계 -> n-ary 관계
- 3원소간의 관계 -> 3-ary 관계
Dom(R) <- 정의역
Ran(R) <- 치역
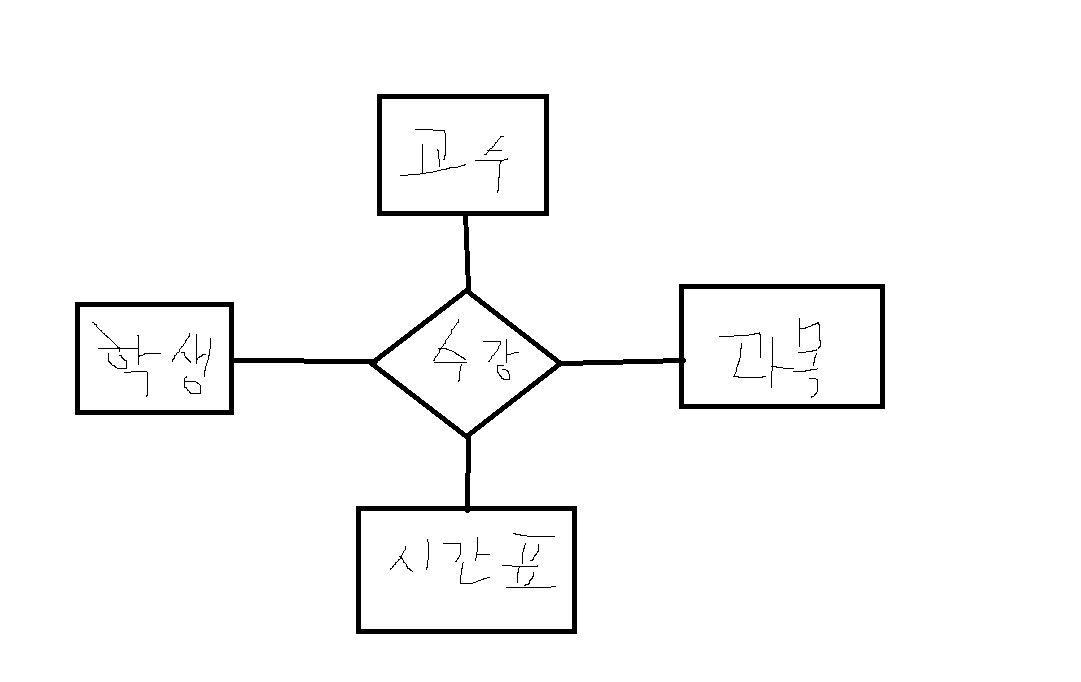
예제 5-1. 두 집합 A, B에서 A={0,1,2}, B={1,2,3}이라고 하자. 집합 A에 있는 원소 x가 집합 B에 있는 원소 y에 대하여, x가 y보다 작을 때 서로 관계가 있다고 가정하고 관계의 집합을 구해보자.
-> (x,y) 단 x<y, x∈A, y∈B
(0,1), {0,2}, {0,3}, {1,2}, {1,3}, {2,3}
예제 5-2. A={1,2,3}이고 A에 대한 관계 R={(1,1),(1,3),(3,2)} 일 때 R은 A * A의 부분집합이기 때문에 A에 관한 관계이다. 이때의 관계를 기호로 나타내고, 관계의 정의역과 치역을 구해보자.
-> 1R1, 1R3, 3R2
정의역 {1,3}
치역 {1,3,2}
예제 5-3. 집합 A={1,2}, B={1,2,3}에 대한 이항관계 R을 다음과 같이 정리해보자.
(a,b)∈A * B
(a,b) ∈R ↔ a-b는 짝수
(1) A B의 순서쌍들과 R의 순서쌍들을 모두 구해보자
A B = {(1,1), (1,2), (1,3), (2,1), (2,2), (2,3)}
R = {(1,1), (1,3), (2,2)}
(2) 1R3, 2R3, 2R2들이 성립하는가?
1. 1-3= -2 (T)
2. 2-3= -1 (F)
3. 2-2= 0 (T)
(3) Dom(R), Ran(R)을 구해라
Dom(R) = (1,2)
Ran(R) = (1,2,3)
예제 5-4. A={a,b}, B={1,2,3}일때 A A, A B, B A, B B를 각각 구해라
A A = {(a,a), (a,b), (b,a), (b,b)}
A B = {(a,1), (a,2), (a,3), (b,1), (b,2) (b,3)}
B A = {(1,a), (1,b), (2,a), (2,b), (3,a), (3,b)}
B B = {(1,1), (1,2), (1,3), (2,1), (2,2), (2,3), (3,1), (3,2), (3,3)}
예제 5-5. 집합 A= {1,2,3}에 대한 이항관계 R이 A의 원소 a,b에 대하여 a>=b일때, 순서쌍 (a,b)로 구성된다. 이때 이항관계 R의 원소들을 구해보자.
R = {(1,1), (2,1), (2,2), (3,1), (3,2), (3,3)}
예제 5-6. A={1,2}, B={x,y,z}, C={3,4}에 대하여 A B C를 구해라.
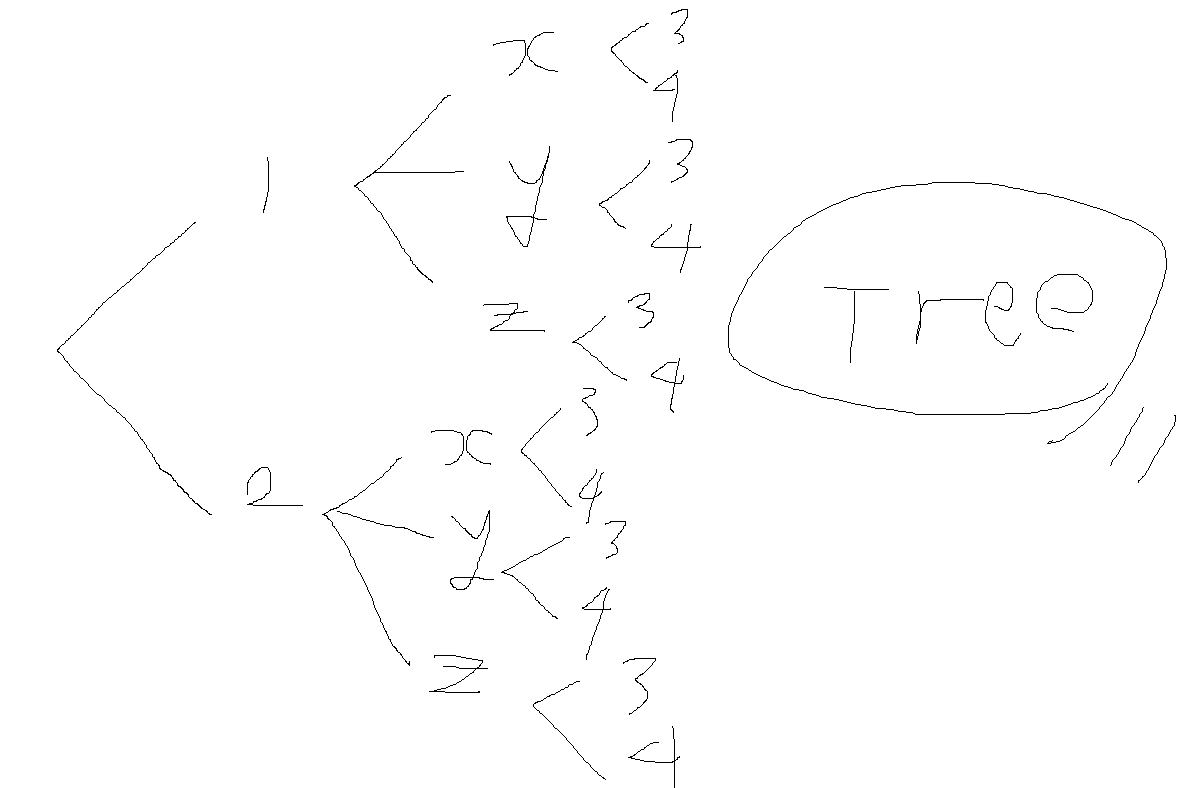
정의 5-3. 집합 A에서 집합 B로의 관계 R에 대한 역관계 R ^ -1는 집합 B에서 집합 A로의 관계를 나타내며, 순서쌍 내의 순서를 다시 바꾸면 그 순서쌍은 관계 R에 속하게 된다.
R ^ -1 = {(b,a)|(a,b)∈R}
-> 다시 말하면, aRb의 관계가 있어야만 (b)R ^ -1가 존재하게 된다.
예제 5-7. 두 집합 A = {1,2,3}, B={3,4}일때 관계 R이 다음과 같다고 하자.
R = {(1,3), (2,3), (2,4), (3,4)}
이때 R ^ -1을 구해라.
R ^ -1 = {(3,1), (3,2), (4,2), (4,3)}
집합사이의 관계를 표현하는 방법
(1) 서술식 방법
- 집합 A = {1,2,3}에서 원소 a,b가 a>=b인 관계 R'과 같이 직접적인 서술식으로 표현함
(2) 나열식 방법
- 순서쌍집합
1) 화살표도표
2) 좌표도표
3) 방향그래프
4) 관계행렬
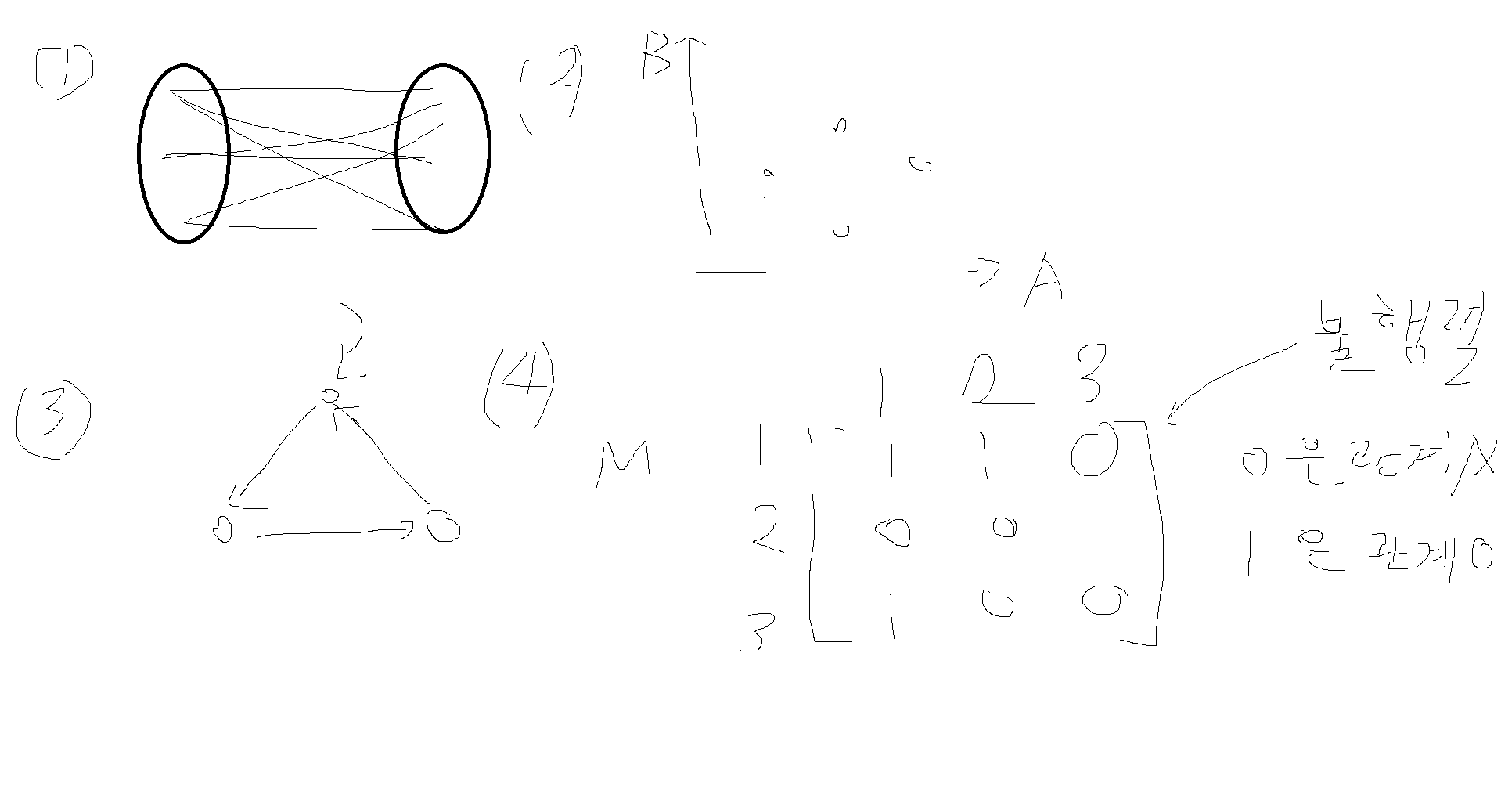
요약
- 두 집합 A, B에 대하여 A로부터 B로의 이항관계 R은 두 집합의 공집합 A * B의 부분집합이다.
- 집합 A에서 B로의 관계 R에 대한 역관계 R ^ -1은 집합 B에서 A로의 관계를 나타내며 R ^ -1 = {(b,a)|(a,b)∈R} 이다.
- 관계표현방식 4가지
연습문제
(1) A={1,2,3}, B={a,b,c,d}, C={4,5}일 때 다음을 구해라.
가) A * B
{(1,2), (1,b), (1,c), (1,d), (2,a), (2,b), (2,c), (2,d), (3,a), (3,b), (3,c), (3,d)}
나) B * C
{(a,4), (a,5), (b,4), (b,5), (c,4), (c,5), (d,4), (d,5)}
(2) 집합 A = {1,2,3,4,5,6}에 대한 관계 R이 R = {(x,y)|x-y=1, x,y∈A}일때 R의 역관계?
R = {(2,1), (3,2), (4,3), (5,4), (6,5)}
R ^ -1 = {(1,2), (2,3), (3,4), (4,5), (5,6)}
